一种基于密度峰值聚类的图像分割算法

赵 军,朱 荽,杨雯璟,许彦辉,庞 宇

(重庆邮电大学 计算智能重庆市重点实验室,重庆 400065)

0 概述

图像分割是计算机视觉和图像处理中的基础部分,其目的在于按照颜色、灰度、纹理等将图像划分成多个不相交的区块,从中提取研究者感兴趣的区域[1]。在计算机视觉领域,对于灰度图像的研究比对彩色图像的研究更为成熟。但随着人工智能的发展,对彩色图像研究方法的需求量在不断增加,针对彩色图像的研究得到了研究者高度重视。

研究者提出许多彩色图像的分割方法,这些方法可分为基于阈值的分割[2-4]、基于聚类的分割[5]、基于边缘或轮廓检测的分割[6-7]和基于区域提取的分割[8]四大类。相较于其他方法,由于聚类是一种无监督的分类算法,不必事先知道分类准则,因此研究者将各类聚类方法应用于图像分割领域,形成诸多基于聚类的图像分割方法,如模糊C均值(Fuzzy C-Means,FCM)聚类[9-11]、K-means聚类[12-13]、谱聚类[14]、Mean-Shift聚类[15-16]、简单线性迭代聚类(Simple Linear Iterative Clustering,SLIC)[17-18]等。其中,有些方法如K-means和FCM在给定聚类数的前提下,能够生成一种分割算法,但算法分割的性能对聚类中心和聚类数敏感,并且多数算法需要人工确定参数。而密度峰值聚类(Density Peak Clustering,DPC)适用于处理任何形状的数据集,无需提前设置簇的数量,所需参数少,算法原理简单容易理解,其复杂度也比一般的聚类算法如FCM和K-means低,但是DPC的可靠性依赖于截断距离的取值和人工确定的聚类中心。

本文提出一种基于DPC的图像分割算法。针对传统DPC中的参数截断距离靠经验取值的情况,引入信息论中信息熵的概念,求得其自适应的截断距离,得到改进后的密度峰值聚类(EDPC),并在EDPC的基础上对彩色图像进行分割。该算法将彩色图像的每个像素点的颜色特征空间作为聚类算法的输入数据,最后基于决策图确定聚类数和聚类中心,实现对图像的准确分割。

1 相关理论

1.1 密度峰值聚类算法

文献[19]提出的DPC算法是一种新型的选取聚类中心的方法,其选取的聚类中心有本身的局部密度大和与其他局部密度大的样本点相对距离较远2个主要特征。基于上述聚类中心的特征,DPC算法计算样本点的局部密度和相对距离,建立决策图,根据决策图选取聚类中心,再对非聚类中心的样本点进行归类合并,从而实现聚类[19]。

DPC算法中的局部密度和相对距离这2个特征分别用参数ρi和δi来刻画,一般选择ρi和δi值较大的点作为聚类中心,实现聚类。

样本点xi的局部密度ρi数学公式定义如下:

(1)

样本点xi的相对距离δi的数学公式定义如下:

(2)

DPC算法原理简单,效率较高,所需参数较少,仅需要局部密度和相对距离2个参数,从式(1)和式(2)可以看出,算法的一个关键参数为截断距离,而参数截断距离dc的选取是基于若干数据集的经验值[20]。截断距离dc一般默认为dij升序排列后前2%处的取值,dc的选取在一定程度上影响着聚类的效果,其值过大过小都会使得聚类效果变差。极端情况下,当dc小于dmin时,每个样本点都是一类;当dc大于dmax时,整个数据集是一类。因此,DPC选取的dc在真实的数据集中分类效果可能不理想。

1.2 信息熵理论

信息论中的信息熵是一种系统有序化程度的度量方法。在一个系统中,某个属性取值提供的信息量越多,系统越稳定,信息熵越小;反之,该属性提供的信息量越少,系统越混乱,信息熵越大[21]。因此,信息熵在聚类分析领域得到了广泛的应用。

对于随机变量X,香农定义的信息熵公式如下:

H(X)=-∑p(xi)lb(p(xi)),i=1,2,…,n

(3)

其中,p(xi)表示为事件xi发生的概率,且∑p(xi)=1。一般信息熵的单位为bit。

2 基于改进DPC的图像分割算法

2.1 改进的密度峰值聚类

针对DPC算法中截断距离dc靠经验取值这一情况,本文提出了一种基于信息熵的截断距离自适应的密度峰值聚类算法EDPC。在EDPC中首先通过信息熵得到自适应的截断距离,然后计算各个参数,画出决策图,根据决策图来选择聚类中心,进行聚类分析。

在DPC算法中,局部密度ρi定义采用离散的密度函数,导致样本点具有相同局部密度的可能性较大,不利于后续研究,因此,本文采用连续高斯核密度函数来刻画局部密度,其相应的定义如下:

(4)

其中,dc∈(0,+∞)为自适应截断距离。

(5)

信息熵作为一种不确定性的度量,被广泛应用于聚类分析中用以判断聚类效果的好坏程度。EDPC将信息熵理论应用到传统的DPC中,用信息熵来判断数据集聚类效果,如果数据集的信息熵较大,则数据集的聚类效果较差,数据较混乱;反之,数据集的聚类效果较好,数据相对较稳定。因此,数据集的信息熵可表示为:

(6)

在EDPC中,假设每个样本点的局部密度概率相等,则数据分布的不确度最大,此时有最大的熵。由式(6)可知,对于具有n个样本点的数据集有0≤H≤lb(n)。对于该算法的高斯核函数,由分析可知,当dc趋近0时,H趋近最大值lb(n);随dc的增大,H首先减小,在某处达到最小值,然后逐渐增大,当dc趋近+∞时,H再一次趋近lb(n)。获得效果最好的聚类效果等价于寻找使得H最小的dc值。因此,本文结合H在(0,+∞)上的变化情况对式(6)中的类信息熵函数H进行求导得到H′,令H′=0来求取极值点处的所有dc值并代入H中,选取使其最小的dc作为自适应的截断距离进行聚类分析。

在真实数据集上验证EDPC算法的有效性,实验结果如图1所示。进一步地,在不同数据集中对比EDPC与DPC的聚类效果,结果如图2所示。在图2(a)中,采用DPC的聚类结果明显地把一类数据划分为了两类,产生了数据误分,而EDPC聚类效果较之更合理,分类更准确;在图2(b)中,DPC聚类边界交叉度高,而且产生了部分数据的误分,而EDPC结果较好;在图2(c)中,DPC聚类结果产生了数据遗失,EDPC保留了完整的数据数目;在图2(d)中,DPC产生的聚类边界相互交叉,聚类边界不明显,而EDPC产生的聚类边界较之更清晰。从DPC与EDPC的对比实验可以看出,EDPC较DPC聚类效果更好,EDPC可以很好的弥补DPC截断距离靠经验取值而导致的在部分数据集上聚类不准确以及聚类边界交叉的不足。实验证明了将信息熵引入到DPC中较好地提升了算法的性能。

图1 真实数据集算法聚类结果

图2 EDPC与DPC在不同数据集上的聚类效果对比

Fig.2 Comparison of clustering effect between EDPC and DPC on different datasets

图3和图4给出EDPC、DPC、FCM 和DBSACN 4种算法在不同据集上的精度值和F值,精度值和F值的取值范围均为[0,1],其值越大表示聚类效果越好。从图3和图4可以看出,在所有数据集上,EDPC算法的性能均优于对比算法。在常见数据集上EDPC算法的聚类结果以及相应的dc如表1所示。

图3 不同算法精度对比

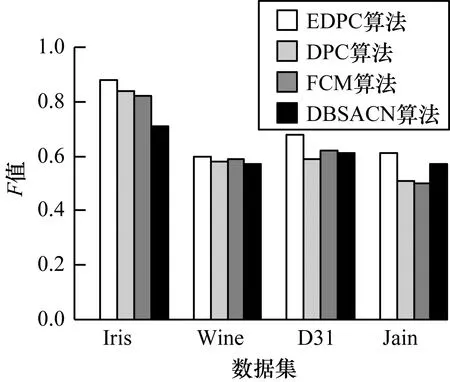
图4 不同算法F值对比

表1 EDPC在不同数据集上的聚类结果

2.2 算法流程

基于DPC算法选取聚类中心的特点,本文提出一种基于EDPC的图像分割算法。该算法首先将输入图像的每一个像素点视为一个样本点,将其颜色空间的CIE Lab值作为样本的特征数据,然后通过计算信息熵求得自适应截断距离dc,从而计算样本点的局部密度ρi以及相对距离δi,建立相应的决策图,最后在决策图中,将ρi和δi都很大的样本点选取聚类中心,确定聚类中心总数,归类非聚类中心点,剔除噪声点从而完成图像分割。

对于图像的像素点,本文修改了DPC算法中的公式。设分割图像中有2个像素点i、j,Lab值分别用(Li,ai,bi)、(Lj,aj,bj)表示,本算法采用欧氏距离作为度量距离,则像素点i、j的欧式距离dij如下所示:

(7)

将得到的距离矩阵应用到EDPC中进行图像分割,算法实施过程如图5所示。

图5 基于EDPC的图像分割流程

基于EDPC的图像分割算法的具体步骤如下:

1)输入待分割的彩色图像,读取原始图像数据。

2)将RGB图像转换为Lab图像。

3)计算每个点与其他点的距离dij。

4)计算信息熵H的极小值,确定自适应截断距离dc。

6)建立决策图,选取聚类中心。

7)将剩余的像素样本点根据EDPC算法进行聚类处理。

8)完成最终的图像分割,输出图像。

3 实验与结果分析

将本文算法与FCM、K-means、IGSO[22]以及IS-FDC[23]算法进行对比实验,验证其正确性以及有效性。实验的图片来源于Berkeley图像分割数据集[24],开发工具为MATLAB R2016b,不同算法的聚类分割结果如图6所示。从图6可以看出,FCM和K-means的图像分割效果较差,分割结果容易受噪声影响,单一的目标和背景容易产生误分,而且生成的像素块模糊程度较高,而本文算法EDPC和IS-FDC以及IGSO受噪声影响小,分割效果更好,目标区域和背景区域比较清晰。从实验结果还可以看出,本文算法针对单一目标和背景差距较大的图片分割效果更好。

图6 不同算法的分割结果

不同算法具体的聚类细节如图7所示。可以看出,在FCM和K-means分割时细节保留不够完整,窗户边缘的窗户框信息遗失,图像分割不完整,聚类边界交叉较多;而采用算法EDPC、IGSO和IS-FDC时,建筑物上的窗户几乎完整地保留了窗户框,细节保留更多,聚类边界清晰,图像分割效果更好。图8在图7基础上展示了不同算法分割后真实图片对比。可以看出,本文算法和IS-FDC较其他算法分割出来的目标建筑更完整,遗失的细节较少。

图7 不同算法的聚类细节比较

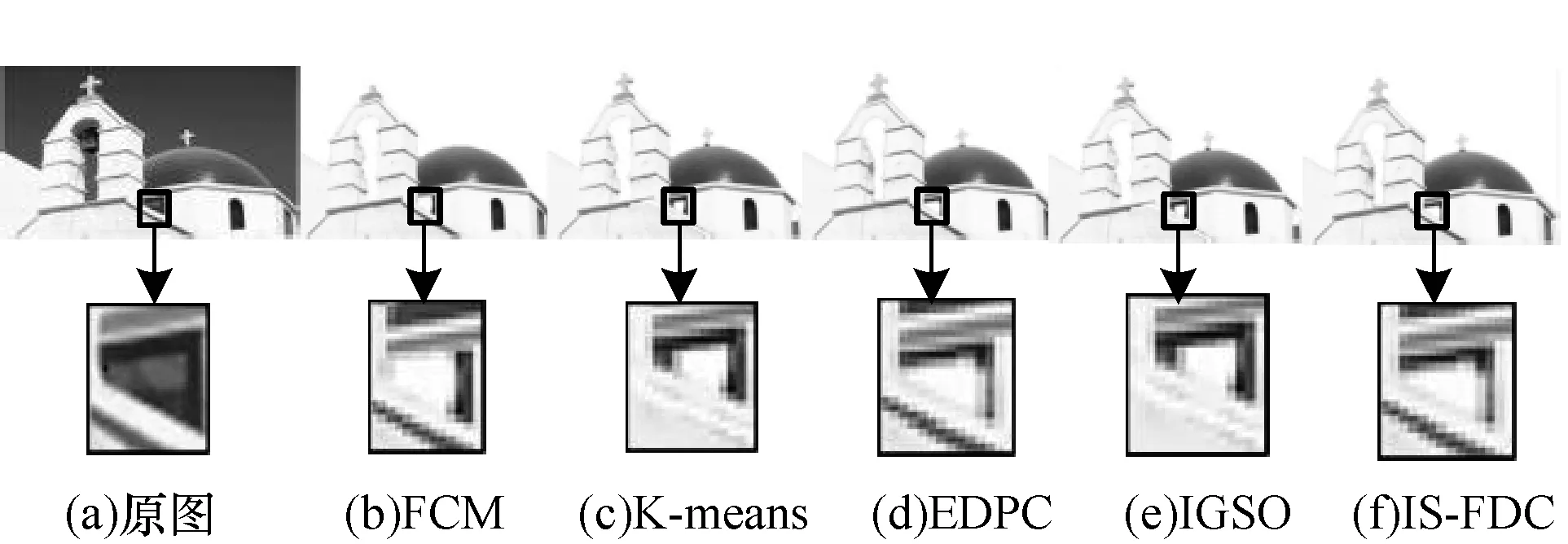
图8 不同算法对真实图片的分割细节结果比较

Fig.8 Comparison of real image segmentation details of different algorithms

为了进一步证明EDPC算法在分割图像方面的有效性和准确性,本文在Berkeley数据集中随机抽取50张图片,计算每种算法的平均分割时间和平均PRI(Probabilistic Rand Index)指标,结果如表2所示。其中,PRI为算法分割结果的准确程度,其取值范围为[0,1],其值越大算法分割效果越好。

表2 不同算法的平均分割时间和PRI指标

Table 2 Average segmentation time and PRI index of different algorithms

指标FCMK-meansIGSOIS-FDCEDPCPRI0.6750.6940.6830.7230.721分割时间/s6.1925.5317.39012.76414.658

从表2可以看出,本文算法在Berkeley数据集上相对于FCM、K-means和IGSO分割效果更好。将EDPC应用到图像分割上,对于像素为n的图像,样本点之间距离的计算时间复杂度为O(n2),虽然算法时间消耗和内存消耗较大,但仍然在可承受范围内。

4 结束语

针对传统DPC算法依靠经验选取截断距离的情况,本文提出基于信息熵的密度峰值聚类算法。通过计算信息熵的极小值获得自适应的截断距离,在此基础上对输入图像进行聚类并分割。在Berkeley数据集中进行对比实验,结果表明,与FCM、K-means和IGSO等算法相比,本文算法受噪声影响小,分割效果较好,其PRI指标为0.721,达到了预期效果。但本文算法未对图像进行预处理,导致分割时间较长,后续将对此进行改进,减少计算数据量,从而提高算法分割速度。