动能拦截器运动伪装末制导律设计

杨 彪，荆武兴，李涧青，高长生

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001；2. 浙江大学电气工程学院，杭州 310027)

0 引 言

动能拦截器在现代防御体系中发挥着重要的作用，它是一种在大气层外利用自己的动能拦截来袭目标的先进武器。动能拦截器的杀伤方式是直接碰撞，这要求其必须具有高精度的制导系统[1]。目前动能拦截器在大气层外主要通过垂直安装的姿轨控发动机提供的常值脉冲推力来实现精确拦截。为了减小发射质量和提高拦截成功率，设计具有制导精度高、消耗推进剂少等特点的动能拦截器末制导律是尤为重要的。

在拦截器末制导律设计问题中，比例导引律以其制导指令形式简单、易于工程实现等特点得到广泛的推广与改进[2]。文献[3]提出了一种偏置比例导引律，根据撞击角和视场角约束设计偏置项来打击机动目标。Prasanna等[4]针对高速目标拦截问题，提出了一种新的比例导引形式，此种制导律具有更大的捕获区域和更小的终端横向过载。此外，最优制导律和滑模变结构制导律等现代制导律也被深入研究[5-6]。文献[7]设计了一个扩展卡尔曼滤波器估计机动目标参数，在此基础上设计的最优制导律具有很高的制导精度。针对机动目标加速度边界未知的拦截问题，文献[8]基于平滑二阶滑模和有限时间收敛扰动观测器设计了一种连续鲁棒冲击角约束制导律，具有广泛的拦截角度和有限时间收敛性。

运动伪装理论最早用于描述生物界捕食者和猎物之间的运动位置关系，由Srinivasan等[9]首次提出。运动伪装理论主要指捕食者、猎物和伪装背景在捕食过程中处于一条直线，从猎物的角度不能明显感知捕食者的位置变化[10]。因其伪装特性具有较大的军事应用价值，近年来也被应用于制导律设计领域[11]。针对导弹制导问题，文献[12]在Frenet框架下建立相对运动模型，设计了一种运动伪装反馈制导律，并比较了不同反馈增益下的制导性能。文献[13]建立了导弹和目标的双二阶动力学模型，在此基础上设计了用于拦截机动目标的运动伪装制导律。一种适用于冲压动力导弹的运动伪装制导律在文献[14]中被提出，可以有效降低命中点的过载，具有较好的制导性能。动能拦截器在末制导过程中，受结构设计的影响，推力为常值脉冲推力并且垂直于拦截器纵轴方向，因此上述制导律生成的连续制导指令不能符合动能拦截器推力大小和方向受限的制导需求。

发动机推力为常值脉冲推力时，采用脉冲宽度脉冲频率(Pulse width pulse frequency,PWPF)调节器可以实现对推力效果的调节[15-16]。文献[17]设计了一种适用于大气层外拦截器的并行逼近制导律，引入阈值评估机制改进PWPF调节器，从而产生制导系统的等效推力。文献[18]针对PWPF调节器参数设置上的局限性,提出了一种非线性优化目标函数,利用提出的优化目标函数,应用遗传算法对PWPF调节器参数进行优化设计。文献[19]主要从飞行器控制效果、发动机开关频率和燃料消耗等方面评估PWPF调节器的性能，并通过模拟和系统分析给出了调节器的最佳参数范围。文献[20]针对大气层外拦截器末制导问题，引入非线性扰动观测器设计了鲁棒性逐渐增强的三维终端滑模制导律，并设计了可变死区的PWPF调节器来适应命中点附近视线角速率变化剧烈的情况。文献[21]在交会对接最终逼近段通过PWPF调节器实现等效变推力，设计了高精度的制导控制律并进行半物理仿真校验。

诸多学者在目标与对象运动模型、保持伪装状态的方法、性能评估等运动伪装理论方面进行了研究；国内外相关文献已经在空间交会、拦截弹等背景领域开展了研究；目前结合具体制导控制执行机构研究该理论还鲜有文献报道，此外，当前的PWPF调节器参数大多通过经验估计或优化方法得出，缺少理论基础。考虑上述制导律和PWPF调节器设计方法在动能拦截器末制导中存在的不足之处，本文首先基于运动伪装理论设计了三维拦截制导律，得到的制导指令作用在视线法向方向。针对动能拦截器推力大小和方向受限的情况，采用PWPF调节器对制导指令进行调节。并结合系统的可控条件和运动伪装拦截条件对PWPF调节器的参数进行理论设计。

1 动力学模型

1.1 拦截器动力学模型

拦截器在飞行过程中，其动力学方程在弹道坐标系下可以表示为：

(1)

式中：vm，θm和ψv分别为拦截器的飞行速度、弹道倾角和弹道偏角；nx，ny和nz分别代表切向过载，法向过载和副法向过载；g为重力加速度，本文统一取值为9.81 m/s2。

1.2 相对运动方程

图1 拦截器和目标相对运动关系Fig.1 Relative motion of interceptor-target

在拦截过程中，拦截器和目标的相对运动关系如图1所示，其中M为拦截器，T为目标。设拦截器指向目标方向为视线方向，则拦截器和目标的相对位置矢量可以表示为：

r=rt-rm=rer

(2)

式中：rm为拦截器位置矢量，rt为目标位置矢量，er为视线方向单位矢量，r为视线长度。

定义视线旋转坐标系由视线方向单位矢量er，视线瞬时旋转角速度单位矢量eω和与二者同时正交的单位矢量eθ构成，即

(3)

式中：ω为视线瞬时旋转角速度，ω为视线瞬时旋转角速率。

根据矢量求导法则可得

(4)

(5)

对式(2)求导可得

(6)

对式(6)求导可得

(7)

结合式(4)和(5)可得

(8)

设am和at分别为拦截器和目标的加速度，在视线旋转坐标系的表达式为

am=amrer+amθeθ+amωeω

(9)

at=atrer+atθeθ+atωeω

(10)

式中：amr和atr为拦截器和目标的切向加速度，amθ和atθ为拦截器和目标的法向加速度，amω和atω为拦截器和目标的副法向加速度。

拦截器和目标的相对加速度可以表示为

(atr-amr)er+(atθ-amθ)eθ+

(atω-amω)eω

(11)

可以导出相对运动关系方程为

(12)

2 运动伪装末制导律

2.1 运动伪装理论

运动伪装指利用视觉特性，使攻击者在目标的侦查视觉中看来与伪装背景(参考点)具有相同的图像特征，使目标不能感受到攻击者的运动特征，从而达到欺骗的效果。运动伪装要求攻击者、目标和伪装背景(参考点)时刻保持在一条直线上，这样会使攻击者与伪装背景的视差最小，攻击者、目标和参考点的相对运动关系如图2所示

图2 运动伪装相对运动关系Fig.2 Motion camouflage scenario

假设目标的位置状态为xt，攻击者的位置状态为xm，参考点的位置状态为xr，记目标和参考点之间的相对位置矢量为

xtr=xt-xr

(13)

设运动伪装控制参数为p(t)，在运动伪装条件下则有

xm=xr+p(t)xtr

(14)

由于运动过程中参考点的位置和控制参数可以任意选取，满足式(14)的运动伪装轨迹有无数条，轨迹的弯曲程度和速度会因选取不同的参数而有所差别。

运动伪装过程中选取的参考点不同会产生不同的效果，如图3所示。当选取的参考点位置为固定伪装背景等有限点时，运动伪装过程类似于制导理论中的三点法；当选取的参考点位于无穷远时，视线方向始终平行，类似于制导理论中的平行接近法。因此基于运动伪装理论的导引方法具有三点法和平行接近法的导引特点。除击中目标外，运动伪装还适用于运动跟踪，运动规避，潜伏到预定位置等，有较大的应用价值。

图3 伪装参考点分类Fig.3 Classification of camouflage reference point

2.2 末制导律设计

基于运动伪装理论，在动能拦截器打击目标过程中，可以将拦截器视为攻击者，逐渐向目标接近。由于动能拦截器在高空进行拦截，目标难以清晰敏感到较远的地表，同时空中也缺乏固定的参考点。因此将参考点设为无穷远处，则有：

r=rr-rm=p(t)er

(15)

拦截器的速度在垂直于视线的方向可以表示为

(16)

同理，目标垂直于视线的速度可以写为

(17)

结合式(16)和(17)可以得到垂直于视线的相对速度矢量

(18)

运动伪装特性的结论[12]有：当且仅当λ=0时，拦截器和目标是处于运动伪装状态下。这一结论说明，当且仅当拦截器与目标在垂直于视线上的相对速度为0时，拦截器和目标处于运动伪装状态。

拦截器最终目的是击中目标，即弹目距离为0，定义比值L

(19)

由式(19)可以看出，由于弹目视线旋转角速率的存在，L值会在-1与+1之间取值。结合式(18)与(19)可得

(20)

(21)

将式(12)代入

(22)

拦截器的制导律可设计为

(23)

则拦截器会满足运动伪装拦截条件，最终成功拦截目标。

证.将其代入式(22)得

(24)

(25)

进而可以得到

(26)

令μ取为

(27)

式中：r0>0，σ>0。

对于任意r>r0有

(28)

当r>r0时，式(24)可以改写为

(29)

由于制导律中包含目标的加速度信息，目标的加速度是有界的，即

|atθ|≤A

(30)

则基于运动伪装的制导律可表示为

(31)

可以看出，在视线旋转坐标系下基于运动伪装理论的制导律只有视线法向上的分量。设计的制导律需要视线旋转角速率、弹目距离、相对速度和拦截器速度等信息，与传统的比例导引律相比需要较多的测量信息，对导引头要求较高。但是引入了相对运动信息，成功拦截机动目标的同时可以保证拦截末端过载较小。

3 PWPF调节器设计

3.1 PWPF调节器

PWPF调节器由一阶惯性环节，施密特触发器和负反馈环节构成，如图4所示。其中E为末制导过程中根据运动伪装制导律得出的制导指令；Km和Tm分别为一阶惯性环节的放大系数和时间常数；Uon和Uoff分别为继电器的开启阈值和关闭阈值；Um为脉冲幅值。在末制导过程中，制导指令E通过PWPF调节器后得到相应的发动机推力脉冲串，实现对制导指令的近似。

图4 PWPF调节器Fig.4 PWPF modulator

根据PWPF调节器的结构框图可知，当发动机处于开启状态时

U(t)=Km(E-Um)(1-e-t1/Tm)+

Uone-t1/Tm,0≤t1≤Ton

(32)

当发动机处于关闭状态时

U(t)=KmE(1-e-t2/Tm)+

Uoffe-t2/Tm,0≤t2≤Toff

(33)

可以解出脉冲开启时间

(34)

脉冲关闭时间为

(35)

发动机的最小脉冲宽度可以在E=Uon时推导得出

(36)

式中：h=Uon-Uoff，上式也可表示发动机的最小工作时间。

PWPF调节器变推力的实现主要和其工作原理中的占空比特性相关，占空比指发动机开启的时间与一个脉冲周期的比值，即

(37)

根据文献[18]可得DC-E曲线如图5所示，其中

(38)

图5 DC曲线Fig.5 DC curve

从图5可以看出，在PWPF调节器作用下发动机的工作状态主要分为三类：(1)E≤Ed时，处于死区状态，此时发动机不工作；(2)Ed≤E≤Es时，处于线性区状态，是调节器的基本工作区，此时通过调节器可以对推力脉冲串进行调宽和调频；(3)E≥Es时，处于饱和区状态，此时发动机持续稳态工作。

3.2 参数设计

上文设计的运动伪装制导律可以在末制导过程中提供连续制导指令，但是这种指令无法直接通过动能拦截器的脉冲推力实现，此时需要利用PWPF调节器来调节推力脉冲，使其能够实现制导指令的作用效果。在此过程中，PWPF调节器的参数对最终效果影响较大，因此有必要针对运动伪装末制导律进行PWPF调节器的参数设计。

根据PWPF调节器的工作区可知，当处于饱和工作状态时，系统必须可控。实际末制导过程中采用直接力的执行方式，发动机输出推力脉冲，输出的推力都是一个确定的数值，此时推力受限的制导律形式可以表示为amθ=Umsgn(ω)，此时可控条件为：

证.令X=ωr，则式(12)可改写为

(39)

选取Lyapunov函数

(40)

其导数为

(41)

将制导律代入可得

(42)

(43)

(44)

根据式(43)和式(44)有

(45)

(46)

若t1时刻制导指令为E=Uon/Km，此时输出为最小脉冲宽度Δ，希望在Δ的作用下，Z值能够收敛至-1，即X=ωr在t1时刻收敛至零，此时amθ=Um，atθ=at(t1)。根据式(39)有

(47)

(48)

令t=t1可得

(49)

综合式(48)与式(49)可得

(50)

令X(t1+Δ)=0可得

(51)

代入制导指令可得

Uon=Km(μvm(Um-at(t1))·

(52)

(53)

4 仿真校验

为了检验本文提出运动伪装拦截制导律的有效性和PWPF调节器设计的合理性，针对高超声速机动目标拦截进行仿真校验。本文选取的初始条件为：目标位置矢量为[170 km,85 km,20 km]；目标速度矢量为[-1000 m/s,-100 m/s,-600 m/s]，大小为Ma3.4；目标在空间内做正弦机动，加速度幅值为9.8 m/s2，周期为100 s；拦截器位置矢量为[130 km,75 km,15 km]；拦截器速度矢量为[1500 m/s,150 m/s,-500 m/s]，大小为Ma4.7。

首先选用真比例导引律(TPN)和运动伪装制导律(MCG)进行对比验证，其中真比例导引系数N取2.3，运动伪装制导律中μ取1.2，A取10。仿真结果如图6至图9所示。

图6 拦截器和目标弹道Fig.6 Interceptor and target trajectory

图7 法向过载Fig.7 Normal overload

运动伪装制导律脱靶量为0.06 m，真比例导引律为0.17 m。由图6和图7可以看出，相对于真比例导引律，运动伪装拦截制导律的弹道更加平直，在制导前期作用在视线法向上的过载较大，所以在制导末期的过载会小于比例导引律的过载。图8表明运动伪装制导律在制导末期视线旋转角速率的变化比真比例导引律更小。运动伪装指标L值的变化如图9所示。拦截末端目标与拦截器距离很近时，视线旋转角速率会变化剧烈，真比例导引律指令主要依赖于视线旋转角变化率，因此过载也会变化剧烈。而运动伪装制导律还引入了相对运动信息，因此可以较好的抑制视线角变化率，过载变化较小。

图8 视线旋转角速率Fig.8 LOS angular velocity

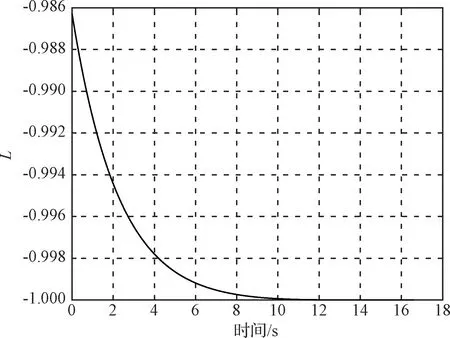
图9 L值变化Fig.9 Variation of L

将运动伪装制导律应用到动能拦截器时，需要利用PWPF调节器。拦截器具体参数如下：质量为60 kg；推进剂质量为25 kg；发动机推力为4700 N；比冲为2800 s。由初始条件可知，拦截器与目标相对距离为41.533 km，相对速度为2514.5 m/s，初始视线旋转角速率为0.01 rad/s，满足第3.2节中的可控条件。则PWPF调节器中Um取值为78.4，最小脉冲宽度选为40 ms，通过式(53)可以选取Uon/Km=9.2，Uoff/Km=0.8。Km取值30，根据式(36)可计算得到Tm=0.38，同时可得Uon=276，Uoff=24。此次仿真中选用真比例导引律进行对比验证，制导参数与上节相同，仿真结果如图10至图15所示。

图10 拦截弹道Fig.10 Interception trajectories

图11 视线旋转角速率Fig.11 LOS angular velocity of interceptor

图12 MCG法向过载Fig.12 Normal overload of MCG

图13 TPN法向过载Fig.13 Normal overload of TPN

图14 L值变化Fig.14 Variation of L

运动伪装制导律和真比例导引律的脱靶量分别为0.08 m和0.21 m。由图10可以看出，相比于图6，增加PWPF调节器后的两种弹道曲线更为接近，这主要因为推力值固定的情况下，运动伪装制导律在制导前期过载较大的情况不会出现。从图11可知在制导末期，运动伪装制导律的视线旋转角速率变化波动较小。图12和图13为两种制导律指令经过PWPF调节器后的视线法向过载曲线。可以看出，采用运动伪装制导律时，因其前期过载较大，前几秒发动机处于饱和工作状态，之后进入线性工作区进行脉冲调频调宽；采用真比例导引律时，发动机基本工作在线性区进行调节。对比两图的过载曲线疏密程度可以看出，运动伪装制导律的过载曲线前期更密集，后期更稀疏，即前期发动机开关频繁，后期开关频率降低。因此会出现图15所示的结果，由于饱和工作和脉冲密集，运动伪装制导律前期消耗更多的燃料，后期消耗较少，整个制导过程中比真比例导引律消耗的燃料更少。图14表明制导满足运动伪装状态。

图15 燃料消耗Fig.15 Fuel consumption

5 结 论

本文结合动能拦截器的具体制导执行机构特点进行了制导律设计。在视线旋转坐标系下建立了相对运动模型，基于运动伪装理论设计了制导指令作用在视线法向的制导律。考虑动能拦截器推力大小和方向受限的特点，结合运动伪装制导律拦截条件对PWPF调节器的参数进行了理论设计，使运动伪装制导律更加符合动能拦截器的制导需求。与真比例导引律进行数值仿真对比，结果表明本文设计的适用于动能拦截器的运动伪装末制导律能够有效拦截目标，并且在命中点附近过载较小，整个制导过程消耗燃料更少。