定量泵可调速平衡回路特性分析

2020-02-18

液压与气动 2020年2期

(贵州大学机械工程学院，贵州贵阳 550025)

引言

液压系统的动态特性是衡量其性能好坏的一个重要指标[1-2]。通过对液压系统进行计算机数值计算，并在模型计算的基础上对其进行优化，对提高系统的动态性能具有十分重要的意义[3-8]。平衡阀和液压缸组成的阀控液压系统是平衡回路中不可缺少的组成部分，平衡阀动态特性的好坏对整个液压控制系统的性能起着决定性的影响。但是国外高性能平衡阀价格昂贵，故而利用平衡阀的性质对系统进行改进，同时在建立系统数学模型的基础上，利用MATLAB强大的数学运算功能对阀控液压缸系统进行数值计算，计算结果与AMESim模型对比，可以很直观反映系统的动态特性。改变系统相关的影响因素利用仿真分析直观反映系统特性，可以为改进平衡回路液压系统提供参考。

1 系统原理分析

1.1 系统设计

设计一种单作用液压缸液压回路和定量泵调速回路结合的平衡回路如图1所示，该系统为平衡回路。

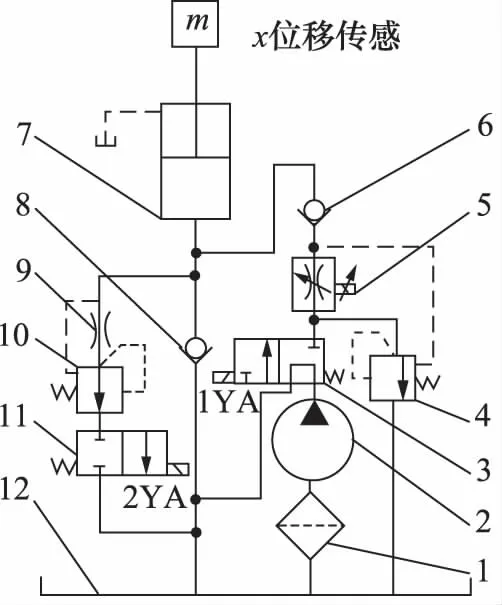
1.过滤器 2.定量泵 3.二位三通电磁换向阀 4.溢流阀 5.电比例节流阀 6、8.单向阀 7.液压缸 9.节流阀 10.减压阀 11.二位二通电磁换向阀 12.油箱图1 系统原理图

1.2 系统工作原理分析

图1所示系统为单作用液压缸平衡回路，存在至少3种工况，如上升、下降和保持。任何平衡回路的建立都需要在上述3种工况的基础上。该系统的平衡阀并非利用传统的平衡阀，而是依靠阀6、阀8和阀11的互相配合，具体分析如下。

对于系统的上升工况，只需要电磁铁2YA断电，电磁铁1YA通电，由液压泵进行供油，供油量的大小可以通过电比例节流阀5的节流口开度进行调节。液压缸活塞承载端与位置传感器进行对比，由程序调节比例阀开口度大小和1YA的通断，可以实现对液压缸的速度和位置控制。

对于静止工况，电磁铁1YA、 2YA断电，此时单向阀8和6对液压缸进行反向锁紧，此时即可实现液压缸的静止工况。由于平衡回路一般都为重载，液压缸内部液压油的压力较大，因而会导致液压缸泄漏量增大。对于长期静止工况会导致液压缸活塞下滑。针对上述情况可以1YA通电，由传感器感应位置误差，通过程序控制比例阀5的开口度可以对液压缸的泄漏油液进行补充，从而起到保持长期静止的效果。液压缸泄漏的油液会进入缸上腔，所以需在其上腔配置一条泄油通道。当系统向上运动时，泄漏到上腔的油液会通过泄油管道，返回油箱。

对于下降工况，只需2YA通电，系统就可以通过自重进行下降动作，由于节流阀9、定差压阀10的存在会有一定的调速作用，但是平衡回路适用于重载，通过阀9、阀10的调速范围有限。此时让1YA通电，对电比例节流阀5控制开口度，可对系统进行供油，由于受到阀9、阀10和负载引起的压力的限制，液压缸下降时的流量会减少，会使得液压缸下降速度减慢，进而表现为速度控制。

综上，该系统可以达到远程无极调速和位置控制的效果。

2 系统性能分析模型的建立

在图1所示的系统中，对系统模型进行简化，并作受力分析如图2所示。将负载G和液压缸质量m进行简化成当量负载F，将出口下降阀通电位于右位工作，简化为通路对其进行分析。

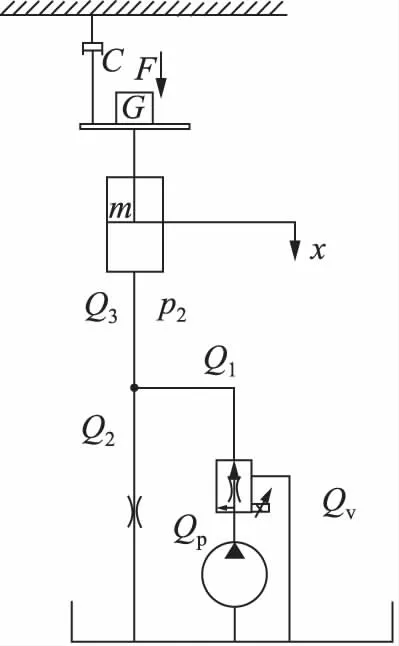
图2 液压缸下降工况模型

现对下降过程中第二种情况进行分析，其他三种情况都可由该工况建模简单的变化得到，由于压力由负载决定，此时液压缸内的压力设为p2，由于泵的出口压力由定差三通阀调定，而三通(溢流)阀的控制油路压力也为p2。电比例节流阀对液压缸供入流量为Q1。此时通过出口节流阀9出口的流量在压差近似恒定和节流口面积不变的情况下约为定值。对电液比例阀动作原理进行分析，电液比例阀阀芯位移工作原理如图3所示。

根据图3建立电液比例节流阀阀芯移动过程微分方程：

Fg=Kii+Ktx1

(1)

式中，Ki——比例电磁铁的电流力系数，N/A

Kt—— 当量弹簧刚度，N/m

线圈的微分方程：

(2)

式中，L—— 线圈电感，H

R—— 线圈电阻，Ω

Ku—— 电压放大系数

Kf—— 电流反馈系数

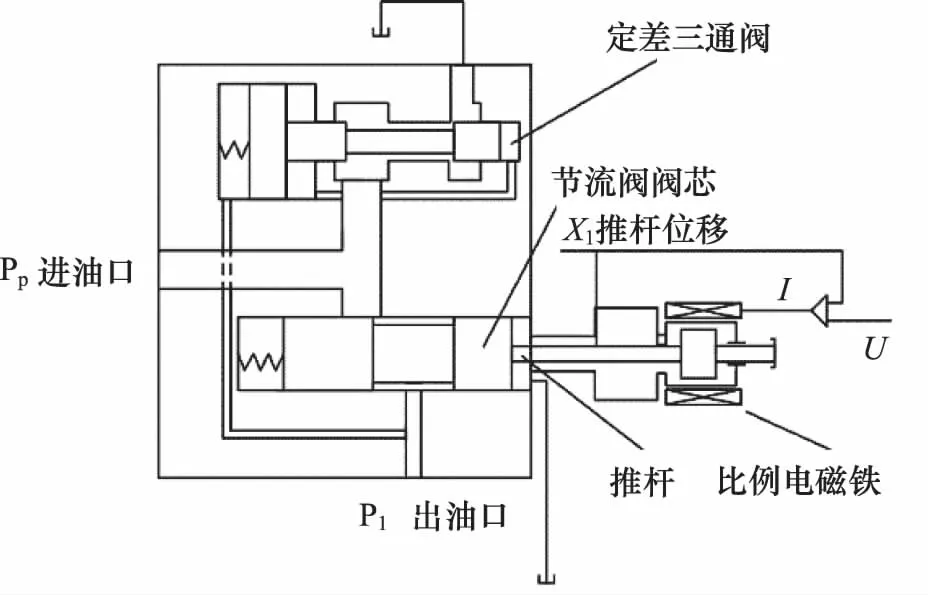
图3 电比例节流阀串接三通阀原理图

推杆受力平衡方程：

(3)

式中，Fg—— 推杆受力，N

mv—— 节流阀阀芯质量，kg

c1—— 阀芯移动粘性阻尼系数，N·s/m

对式(1)～式(3)进行拉普拉斯变换并化简通电液比例阀开口度传递函数为：

(4)

此时通过电比例节流阀流量为：

Q1=Qp-Qv

(5)

通过电比例节流阀节流口流量：

(6)

对上式进行线性化并写成增量形式：

Q1(s)=KQ1ΔAJ+KP1Δp1

(7)

因为采用三通阀实质是一个定差元件Δp1=0，流量只与节流口开口大小有关即：

Q1(s)=KQ1ΔAJ

=Kx1

(8)

此时液压缸的流量：

(9)

通过二通阀的流量：

Q3=Q2+Q1

(10)

通过二通阀的节流口流量：

Q3=KQ3ΔAJ3+KP3Δp2

(11)

由于阀9节流口是固定节流口大小不变ΔAJ3=0，过节流口流量：

Q3=KP3Δp2

(12)

液压缸的受力平衡方程：

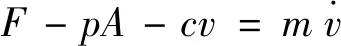
(13)

溢流阀溢流量方程：

(14)

故可得该工况下的微分方程组：

(15)

3 MATLAB模型分析

本研究直接对第三种工况，即下降过程中发现下降速度过快，对下降速度进行调节的工况进行分析。第一种工况是对第三种工况的2YA断电实现。第二种工况只是需1YA，2YA断电，泄漏时1YA通电，通过比例阀补油。因而第一、二中工况便不再进行数值分析。

系统短时运动泄漏量很小，可忽略不计将系统运动微分方程组(15)写入MATLAB，微分方程组函数如下：

function xdot=myfun 42(t,x)

上述方程组中：

x[1,2,3,4,5,6,7]=[x,v,p1,pp,x1,v1,i1]

本系统研究对象为山地农用起重机械工作平台，该系统初始工作压力为6.5 MPa，核算负载力为62000 N，在液压缸行程1.5 m的一半位置发现速度过快，电比例阀参数查询机械设计手册，流量增益与阀芯直径和流量系数等计算后折算为K，其余各参数大小通过模拟工况设计计算整定，取值如表1所示。

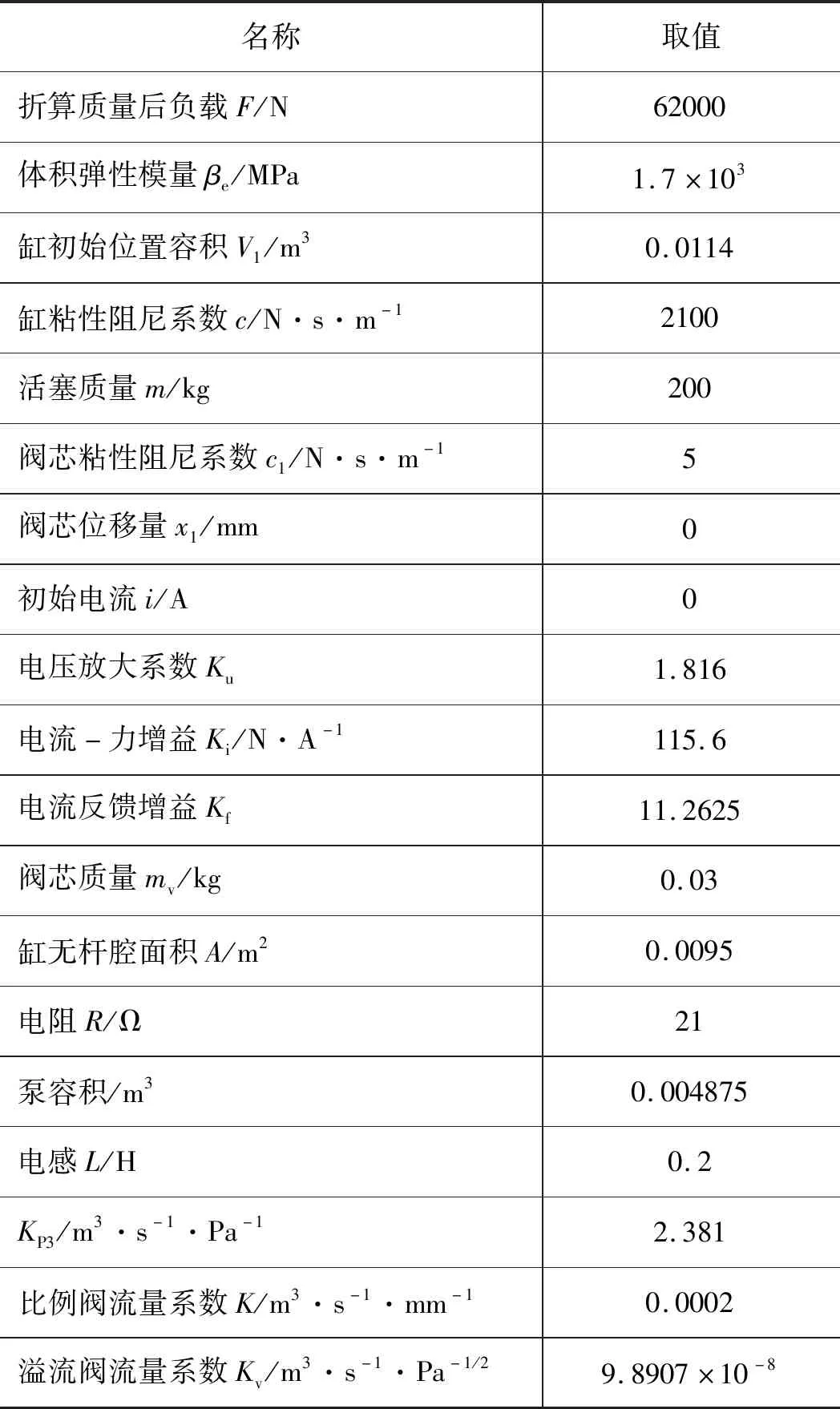
表1

将上述初始条件与参数带入微分方程矩阵并进行求解：

x0=[0, 0.15, 6.3×106, 8.5×106, 0, 0, 0]

[t,x]=ode45(@myfun,t,x0)

建立AMESim模型，AMESim仿真分析结果作对比。

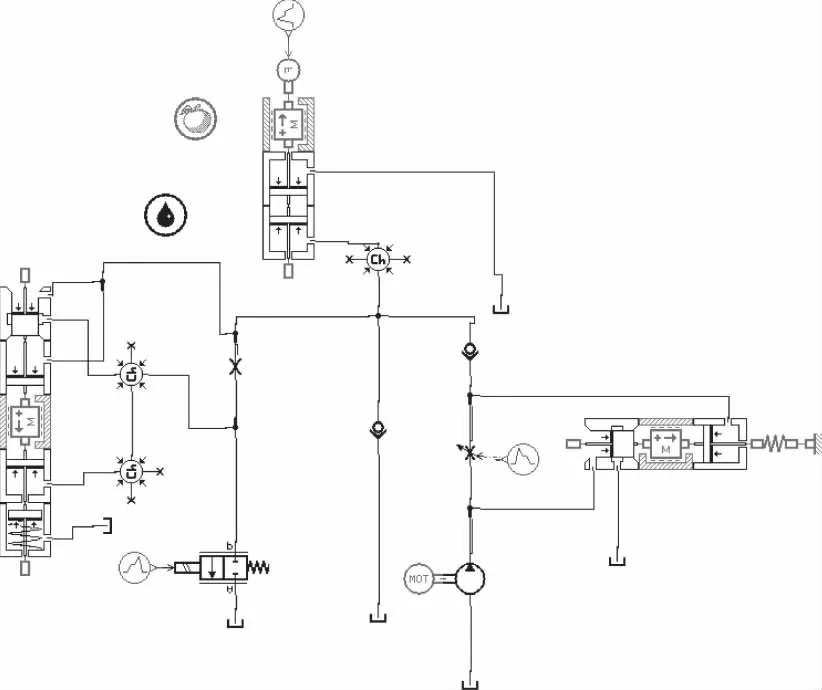
图4 AMESim模型

对上述系统微分方程运用龙格库塔4阶5步法进行求解，和运用AMESim仿真，对第三种工况用上述微分方程进行求解，可得液压缸在运动过程中的特性。设定初始速度为0.15 m/s下降，在此情况下对改变电比例节流阀阀芯移动来达到控制下降速度的目的，数值计算结果如图5～图7所示。

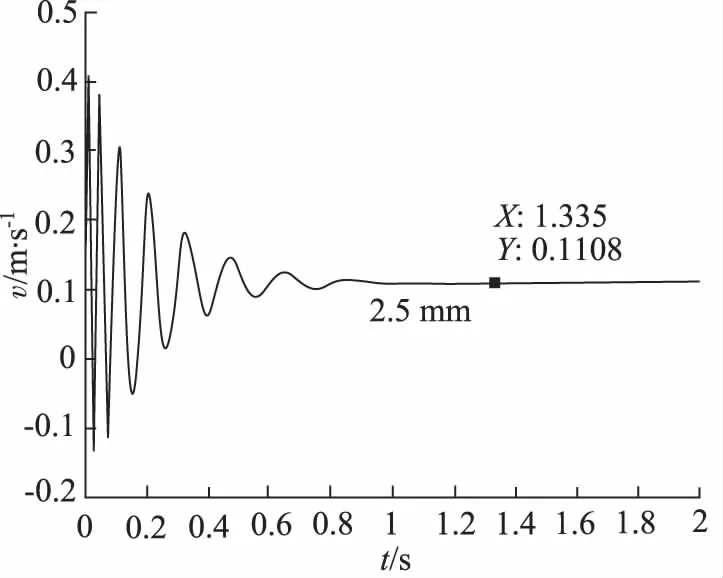
图5 比例阀开度为2.5 mm时速度图

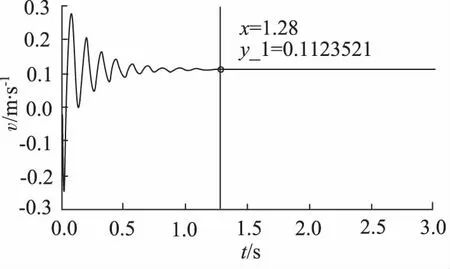
图6 AMESim模型仿真分析图

(1) 如图7所示，在电比例节流阀阀芯移动下，通过电比例节流口的流量增多，而通过出口节流阀的流量近似为定值，导致液压缸的下降速度由0.15 m/s，下降至0.11 m/s，这种情况对于低速重载工况，改善已经很明显了。出口是定差减压阀串接一个节流阀，故而能够保证液压缸的运行平稳。

如图7、图8所示，初始情况出现一定的震荡，短时间内系统自动调节，位移和压力都很平稳。

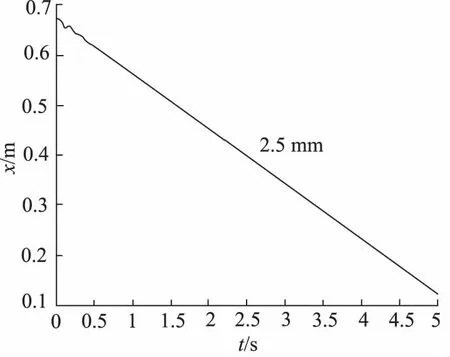
图7 三通阀开度为2.5 mm时位移图

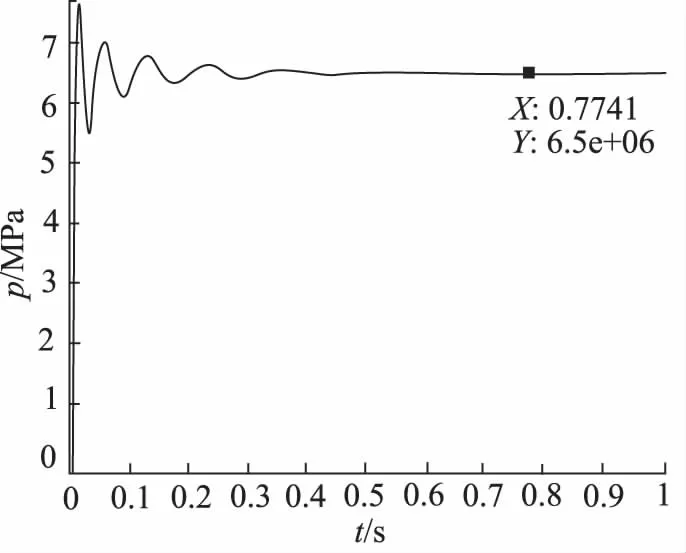
图8 比例阀开度为2.5 mm时压力图

(2) 上述数值计算结果表明我们可以通过电信号调节电液比例阀电磁力的大小，即调定电压量来控制节流口开度大小，通过上述操作，可达到对液压缸流量的控制，计算设定开度分别为2.5， 4.5， 7.5 mm，计算结果如图9～图11所示。

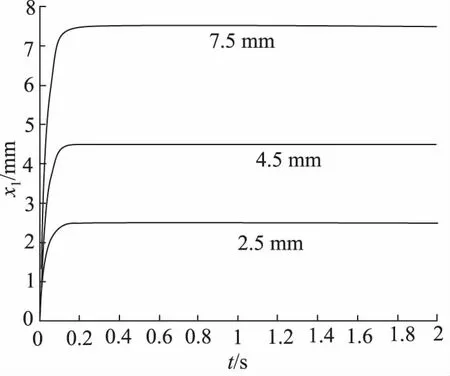
图9 变更电信号电比例阀芯位移图

图10 Simulink比例阀开口图

图11 电比例阀阀芯不同开口度速度图

图7结果表明通过调定电压信号，电比例阀的阀芯移动导致开口量变化。从而致使液压缸的流量发生变化，导致液压缸速度发生变化如图11所示。如图12所示，压力由负载决定，因而改变电比例阀节流口对压力变化影响不大，数值计算结果与理论分析结果近似一致。

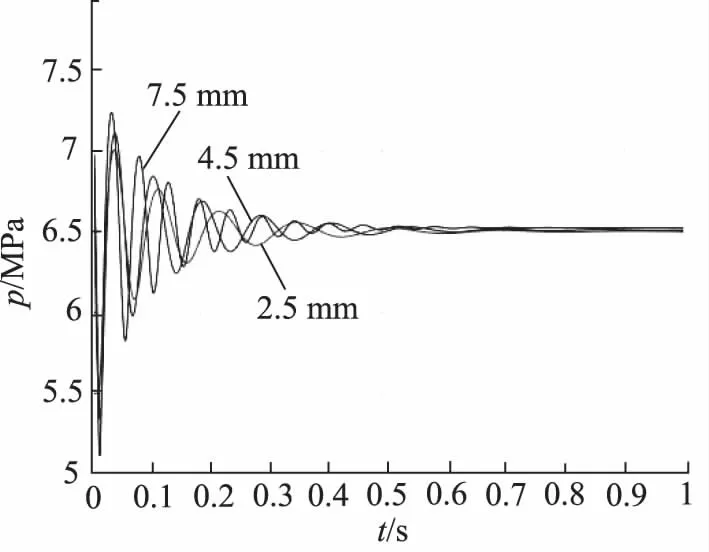
图12 比例阀阀芯不同开口度时压力图

(3) 通过对外负载的改变也可以达到改变液压系统特性。由于回油路采用节流阀串接定差压阀，即使液压缸的压力出现变化时，节流阀内定差元件自动补偿，从而可以保持回路的速度近似恒定，计算结果如图13、图14所示。

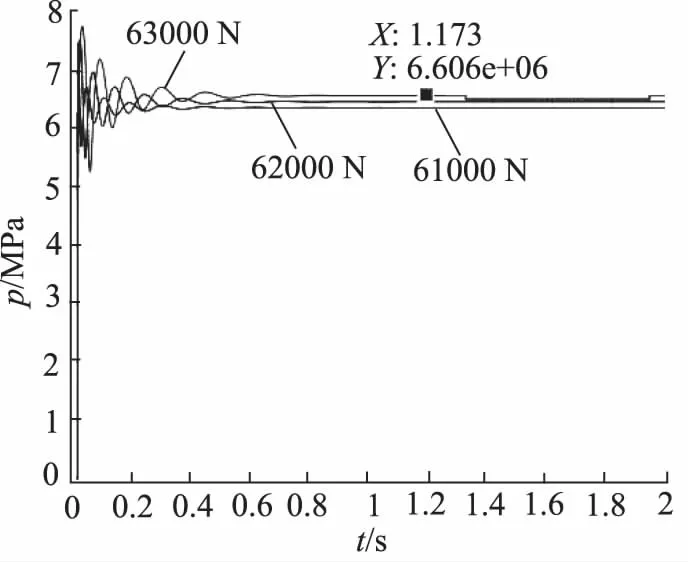
图13 负载变化时压力图

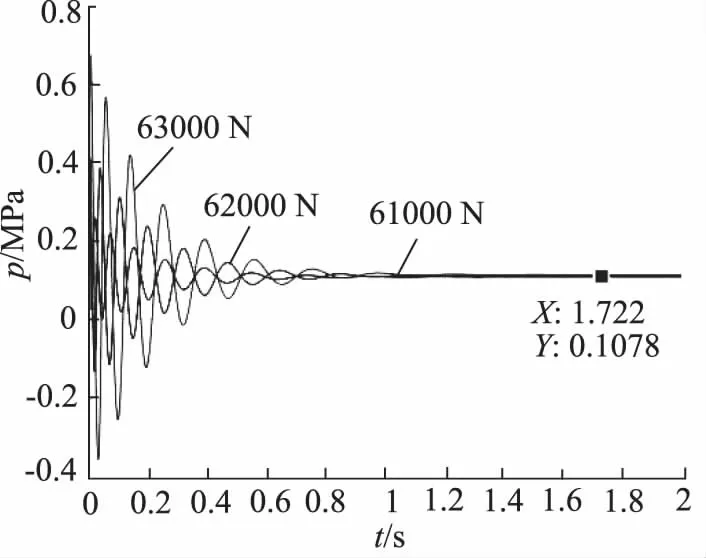
图14 负载变化时速度图

如图13所示，数值计算结果表明外负载变化导致液压缸的压力变化。但是出油口接的是二通阀，实质是定差元件串接一个节流阀，节流阀的阀前阀后压力分别通过控制油路到达定差元件的两端，故而进出油压力差仍然只与定差元件弹簧力有关。如图14所示，输出的流量仍然恒定，不受外负载变化的影响。计算结果表明下降的速度不会因外负载的变化而变化，故而数值计算与理论分析结果一致。

图15 节流阀节流口大小变化时速度图

(4) 变更出口节流阀节流口大小也可以改变该系统的特性，该系统中二通阀节流口初始设定大小为5 mm，现变更改参数，计算结果如图15、图16所示。

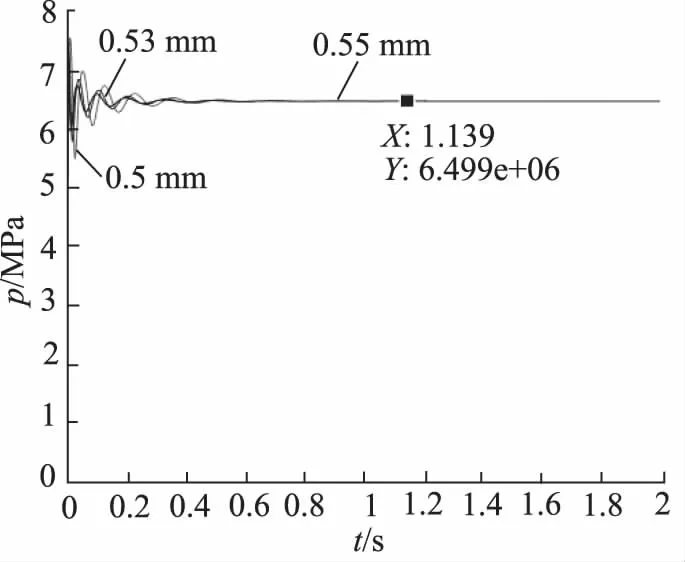
图16 节流阀节流口大小变化时压力图

节流口大小变化使得通过节流口的流量变化，由于电比例节流阀开口固定压差固定，因而两者之差会发生变化，即液压缸的流量发生变化就致使速度发生变化，如图15所示。节流口面积增大时，液压缸速度也会增大。而系统压力由外负载决定故恒定，变节流口不会导致液压缸压力变化，如图16所示。计算分析结果与理论分析结果一致。