正常使用极限状态下隐式功能函数结构可靠度计算

金波　周旺　唐丽莹　李梓溢　姜早龙

摘   要：提出了一种适用于具有复杂隐式功能函数的钢桁架结构可靠度计算方法. 采用神经网络逼近正常使用极限状态下隐式功能函数，基于可靠度指标的几何意义，运用新改进的遗传算法搜索钢桁架可靠度指标最优解及验算点. 通过两个算例，分别使用JC法和蒙特卡洛重要抽样法验证了新改进的遗传算法的准确性和有效性. 结果表1明，新改进的遗传算法与蒙特卡洛法计算的钢桁架可靠度指标相对误差仅为0.23%;且对于小概率失效结构，引入的自适应随机变量能有效改善传统方法中初始种群基因不良的问题. 該方法在计算复杂隐式功能函数结构可靠度指标时，具有计算速度快、计算简单、精度高等优点.

关键词：可靠度指标;隐式功能函数;神经网络;遗传算法

中图分类号：U442.5                               文献标志码：A

Reliability Calculation of Implicit Function

Structure in Service Ability Limit State

JIN Bo？，ZHOU Wang，TANG Liying，LI Ziyi，JIANG Zaolong

（College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract：A reliability calculation method is proposed to calculate the reliability of structure with complex implicit function like steel truss structures. It firstly adopts the neural network to approach the implicit function in service ability limit state and NGA （New Genetic Algorithm） is employed to obtain the optimal solution of reliability index of steel truss structures and its design point on the basis of the geometric implication of reliability index. Finally，JC method and Monte Carlo Critical Sampling Method are introduced，respectively，in two examples to verify the accuracy and validity of NGA. The results manifest that the relative error is only 0.23 percent when NGA and Monte Carlo Method are used，respectively，to calculate the reliability index of steel truss. In addition，the introduction of adaptive random variable can greatly improve the gene of initial population for small probability failure structures. All above prove that NGA is of significance in practical projects for calculating the reliability index of structure with complex implicit function due to its advantages of fast computation speed and high precision.

Key words：reliability index;implicit function;neural networks;genetic algorithms

金波等：正常使用极限状态下隐式功能函数结构可靠度计算

保证结构在规定的使用期内能够承受设计的各种作用，满足设计要求的各项使用功能，保证结构的安全性、适用性与耐久性，这三个方面构成了工程结构可靠性的基本内容. 结构可靠度是结构可以完成“预定功能”的概率量度，通常采用“极限状态”来衡量预定功能，工程结构中的极限状态可分为正常使用极限状态与承载能力极限状态. 在实际工程中存在诸多不确定性，如材料性能、外荷载、制作安装等变异. 这些变异是随机的，可靠度分析是建立在统计数学的基础上，予以可靠性一个定量的描述.

在实际工程中结构往往为多次超静定结构，其变量与响应难以用显式关系表1达，而且功能函数具有非线性、复杂性、多峰性等特点. 因此，钢桁架的功能函数显化难度大，甚至无法显化[1-4]. 另外，结构失效为小概率事件导致可靠度计算工作量大. 传统的一次二阶矩法、二次二阶矩法、响应面法、蒙特卡洛法虽然理论成熟，但都是以显式功能函数为前提的，因此不适用于小失效概率复杂隐式功能函数结构的可靠度计算.

文献[5]通过引入差分法，解决了隐式功能函数不能理论求解偏导的问题，并计算了隐式功能函数结构的可靠度，其计算过程较繁琐且未考虑截面尺寸的随机性对结构响应的影响. 文献[6]采用传统的遗传算法与BP神经网络结合的方法对斜拉桥的可靠度进行计算. 但BP神经网络具有学习过程冗长、容易陷入局部极值等缺点;传统遗传算法存在“早熟”，陷入局部最优，收敛速度慢等不足. 文献[7]提出了将均匀设计法、径向基神经网络技术和最大熵原理相结合对边坡进行可靠性分析的四阶矩计算方法. 文献[8]采用径向神经网络、β约界法、概率网络评估技术与蒙特卡洛结合的方法求解了钢桁架的可靠度指标. 文献[9]通过建立标准化屈曲安全余量方程，采用逐步等效线性化Johnson求交法计算了输电塔的结构可靠度. 文献[10]通过随机有限元法和结构系统可靠性理论，建立桁架结构单元的安全余量的表1达式，对桁架结构系统进行可靠性分析. 文献[11]将一次可靠度确定验算点与响应面法的思路相结合，并引入单边差分法针对性地解决了隐式功能函数求偏导数的问题，确定各分量函数的二次多项式近似，从而获得近似的整体功能函数，最后采用蒙特卡洛法进行计算，计算过程较繁琐，且对于小概率失效结构，蒙特卡洛法求解计算量巨大. 国内外学者在复杂隐式功能函数可靠度计算上做了大量工作，但难以有效协调计算精度、计算量及方法适应性等方面的要求进行可靠度计算.

为提高具有复杂隐式功能函数的小概率失效结构可靠度计算的速度与精度，通过引入自适应随机变量与遗传算子的改进对自适应遗传算法进行优化. 采用泛化能力更好的径向神经网络逼近钢桁架的隐式功能函数，基于可靠度指标的几何意义，运用新改进的遗传算法搜索钢桁架可靠度指标最优解. 该方法能更加精确地逼近复杂隐式结构功能函数，有效解决小概率失效结构可靠度求解中带来的精度不足、过程复杂与计算量大等问题.

1   新改进的遗传算法（NGA）

对于具有复杂性、非线性、非凸性、多峰性功能函数的结构，其可靠度指标是极限状态曲面与坐标原点多个局部极小距离中的最小距离. 为避免计算过程中产生局部极小值问题，提高计算结果可靠性，可采用遗传算法这类具有全局最优搜索能力的算法. 但传统的遗传算法容易出现局部“搜索能力不足”“欺骗”以及“早熟”等问题，针对以上问题对传统遗传算法进行了改进.

1.1   改进遗传算法的编码方式与随机变量的产生

为便于对所有连续变量进行统一编码，在不改变随机变量取值范围的前提下，将所有随机变量的产生转化到[0 1]中，传统方法产生服从正态分布随机变量xi，可按式（1）计算.

xi = ui + σisin（2πγ3）.    （1）

式中：γi為[0，1]上相互独立的均匀分布随机数.

由式（1）可知，基于二进制编码及γi在[0 1]上服从均匀分布的特点，采用二进制进行编码.

但式（1）中含有自然对数，自然对数的值域在0附近分布密集，在[0，1]区间采用均匀分布产生随机变量时，大量有效的点将会被忽略. 由图1可知，当二进制步长为0.001时，按均匀分布产生的随机变量大约分布在[-3，3]区间，但随机变量的取值应该为

[-∞，+∞]，同时对于小概率失效结构，最优解距中心点的距离较远，故采用传统产生随机变量的方法，不能满足遗传算法初始变量的要求，甚至导致可靠度计算失败. 为提高随机变量的适应性，根据失效概率的大小，通过引入自适应随机参数进行改进以改善自然对数对随机变量的影响，从而扩大初始变量距中心点的距离，达到改善遗传算法初始种群中不良基因的目的.

设x为已知分布特征的随机变量，可按式（2）（3）（4）产生服从正态分布、对数正态分布和极值Ⅰ型分布的随机变量.

正态分布：

xi = ui + aγ1σisin（2πγ3）.    （2）

对数正态分布：

[        σy = σln x = ，

uy = ln ux - σ2

ln x = ln，

yi = uy + aγ1σysin（2πγ3），

xi = e.                        ][ （3）]

极值Ⅰ型分布：

xi = ui - 0.5σi - 0.779 7aγ1σi ln（-lnγ2）.    （4）

式中：a为变量自适应参数，可根据失效概率进行调整.

1.2   改进遗传算法的基本操作

通过改变传统遗传算法的交叉率、变异率及加入精英保留策略，能使种群中最大适应度个体的交叉和变异率不为零，从而增加算法跳出局部极小值问题的可能性，自动调整适应度，有效地保护最优个体不受损害及加快收敛速度. 新改进遗传算法的基本操作如下.

1）选择. 采用轮盘赌，按照适者生存的原则，使适应度高的个体生存，低的淘汰.

2）交叉. 采用改进的二进制单点交叉法，两个染色体在同一位置截断，其相应位置交叉组合成两个新的染色体. 在进化过程中，通过式（5）对交叉率进行自适应调整.

Pc =

，f ′≤ favg，

，f ′> favg. （5）

3）变异. 染色体复制时以很小的概率产生复制

差错，形成新的染色体. 在进化过程中，通过式（6）对交叉率进行自适应调整.

Pm =

，f ≤ favg，

，f  > favg. （6）

式中：fmax表1示种群中最大适应度值;favg表1示每代群体的平均适应度值;f ′表1示要交叉的2个个体中较大的适应度值;f表1示变异个体的适应度值;Pc1、Pc2、Pc3为区间（0，1）内表1示给定的交叉概率值，Pm1、Pm2、Pm3为区间（0，1）内表1示给定的变异概率值，且有Pc1 > Pc2 > Pc3，Pm1 > Pm2 > Pm3.

1.3   适应度函数

遗传算法中，可以通过引入罚函数将有约束问题转化为无约束问题. 功能函数为z = 0，以搜索目标函数的最小值为目标，适应度函数如式（7）所示.

fit（x） = .     （7）

式中：c为β（x）的保守估计值;mz为惩罚项，m为惩罚因子，取值一般很大.

2   基于RBF-NGA法可靠度计算

2.1   RBF神经网络拟合隐式功能函数

在实际工程可靠度计算中，结构失效一般为小概率事件，且结构的功能函数具有非线性、复杂性、多峰性等特点，导致可靠度计算时计算量大、显化难度大与精度难以满足甚至无法用显化的方程表1示. 对隐式功能函数，利用数值模拟或试验方法得到结构的变量与响应，以此作为神经网络的输入和输出对神经网络进行训练和测试. 训练好的神经网络能较好地逼近结构的功能函数.

径向基函数（Radial Basis Function，RBF）神經网络是一个三层前反馈型神经网络. 径向网络能够根据用户设定的目标误差，自适应地增加网络的隐含层节点数量，直到满足目标误差要求，无需用户指定隐含层节点数. 以精确映射出结构各个隐式功能函数为目的构建神经网络，能更加精确地逼近结构功能函数，该方法避免了对功能函数的显化、拟合功能函数的精度不足、计算量大等问题. 采用MATLAB 13a神经网络工具箱中提供的神经网络设计和拟合函数. 函数如下所示.

1）RBF神经网络学习函数newrb. 调用格式为：

net=newrb（P，T，goal，spread，MN，DF）

其中：P为输入矩阵;T为目标输出矩阵;spread为RBF的扩展常数;goal为网络的均方差;MN为网络学习过程中神经元的最大数目;DF为两次显示之间所增加的神经元数目.

2）RBF神经网络仿真函数sim. 调用格式为：

Y = sim（net，X）

其中：net为学习好的径向基神经网络;X为输入测试矩阵;Y为预测值.

在训练神经网络时，为减少神经网络的样本点数量，需采用更高质量的训练数据. UD（均匀设计）[12]与正交设计相比，有更好的均匀性，且同样试验次数可安排更多的水平数，采用DPS[13]（数据处理系统）的均匀试验设计功能，通过多次迭代可生成更高质量的均匀试验设计变量.

为提高计算响应的效率，采用Python多线程调用ANSYS批量计算均匀设计变量的结构响应，其具体操作流程如图2所示.

最后将变量和结构响应归一化后作为网络的输入和输出，构建钢桁架的功能函数.

2.2   可靠度指标的几何意义

可靠度指标β在标准独立正态坐标系中等于原点到极限状态曲面的最短距离，其对应在失效面上的点即为验算点. 设具有n个独立正态分布变量的极限方程为g（x） = g（x1，x2，…，xn），将变量标准化，[x]i =（xi - ui）/σi，其中ui、σi分别为变量的均值和标准差. 极限状态方程可改写为z = g（u

x1+ [x]1σ

x1，…，u

xn+

[x]n σ

xn），故β在标准正态空间中按式（8）计算.

β（x） = min

，

g（[x]） = g（[x]1，[x]2，…，[x]n） = 0. （8）

对于服从一般分布的随机变量，可进行高斯变换，将一般分布当量成正态分布. 高斯变换如[x]i = ？-1[Fi（xi）]，其中：Fi（xi），？-1[Fi（xi）]分别为随机变量xi的CDF和标准正态分布的CDF.

2.3   RBF-NGA方法的可靠度计算

传统的蒙特卡洛法及一次二阶矩法难以实现具有隐式功能函数钢桁架的可靠度指标的计算[14].事实上基于可靠度的几何意义，可采用RBF神经网络逼近复杂功能函数供具有全局搜索能力的NGA调用，搜索可靠度指标.

由式（2）～（4）可知，只需对γi产生均匀随机数就可得xi的取值，即可靠度指标可表1示为γi的函数，则式（1）可改写为式（9）.

β（x） = min f（γ1，γ2，…，γm），

g（[x]） = g（γ1，γ2，…，γm） = 0.      （9）

根据式（9）以RBF神经网络构建好的隐式功能函数为约束条件，运用自编的NGA计算可靠度指标β. RBF-NGA的计算过程如图3所示.

3   工程算例分析

3.1   例1：较大概率失效结构可靠度计算

已知非线性极限状态方程为g = 567fr - 0.5H2 =0，参数取值及分布见表11. 采用NGA分别计算传统随机变量方法与式（2）～（4）产生随机变量方法计算可靠度指标，结果见表12.

采用3个标准节建立ANSYS计算模型. 荷载布置在每个标准节平联杆的1、2、3、4位置，如图5所示.

3.2.2   RBF神经网络构建钢桁架功能函数

考虑到失效模式为位移失效的情况，可从位移限值的角度构建钢桁架的复杂隐式功能函数，以正常使用极限状态下结构的最大竖向位移构造功能函数. 其功能函数如式（10）所示.

z = umax - u（x）.     （10）

式中： umax为正常使用极限状态下位移限值; u（x）为各随机变量对应的钢桁架的最大竖向位移.

考虑到材料截面尺寸的制作和安装误差、荷载的不确定性，以钢桁架的高度H、横架的截面高度h1、宽度w1和腹杆截面宽度w2为不确定性变量. 各变量的设计值分别为H = 7 500 mm，h1 = 800 mm，h2 = w1 = 640 mm，w2 = 340 mm，外荷载F = 550 kN. 不确定性范围取±10σ. 先采用DPS生成U400（4005）的均匀设计样本作为RBF神经网络的输入，设计变量取值范围、分布类型及参数见表13.

再根据图3流程，计算各个样本值对应钢桁架的最大竖向位移，最后均匀设计变量与最大竖向位移分别进行归一化处理后，采用MATLAB中的RBF神经网络工具箱构建钢桁架的功能函数. RBF神经网络参数见表14，测试网络精度如图6所示.

根据RBF神经网络预测和ANSYS计算结果，最大竖向位移神经网络预测值与ANSYS计算值最大相对误差为1.88%. 由图6可看出，在有限组变量下，RBF神经网络拟合精度高，得到泛化能力较好的神经网络.

3.2.3   钢桁架可靠度计算

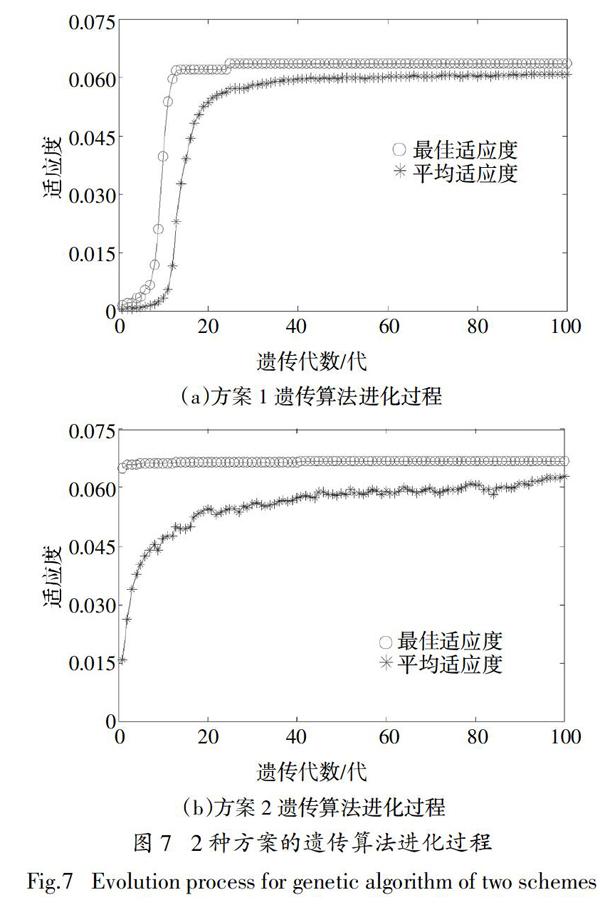
按照图3所示流程分别按传统的方法产生遗传算法随机变量（方案1）与按式（2）～（4）自適应产生随机变量（方案2）两种方案，采用自编的NGA程序（参数见表15，两种方案进化过程如图7所示）搜索钢桁架的可靠度指标及验算点.

对于小概率失效结构，若直接采用蒙特卡洛模拟方法，则效率和精度都较低. 若以NGA搜索的验算点为蒙特卡洛抽样中心，则能使样本点有更多机会落入失效区域，增加功能函数小于0的机会，从而有效提高蒙特卡洛法的效率和精度，并以此验证NGA的准确性和有效性. 采用蒙特卡洛法在方案2搜索的验算点处进行重要抽样（108次）（可认为是精确解），结果见表16.

从图7、表16可看出，对于小概率失效结构，传统方法产生的初始种群适应性较差，种群的平均适应度、最佳适应度、进化后期个体多样性都不理想. 且搜索的最优解与蒙特卡洛法的相对误差为13.89%，难以实现小概率失效结构可靠度的准确计算.

自适应随机变量方法根据结构失效概率自适应调整随机变量分布，使初始种群个体更集中于适应度大的个体. 从进化图（图7）中可看出，产生的初始种群适应性良好、进化过程保存了个体的多样性，优化了小概率失效结构可靠度的计算过程. NGA进化到第25代左右时已收敛，且与蒙特卡洛法相对误差仅为0.23%，进一步验证了NGA收敛速度快、计算精度高的优点.

4   结   论

基于本文提出的一种适用于具有复杂隐式功能函数的钢桁架结构可靠度计算方法，采用RBF-NGA算法计算可靠度指标，通过两个算例，得到如下主要结论：

1）采用均匀设计变量构建的RBF神经网络，网络预测值与ANSYS计算出的最大位移值最大相对误差仅为1.88%，说明RBF神经网络方法能很好地拟合复杂结构隐式功能函数.

2）在小概率失效结构可靠度计算中引入的自适应随机变量较好地改善了传统方法随机变量的适用性和遗传算法中不良基因.

3）采用NGA计算具有复杂隐式功能函数结构

可靠度指标的结果与蒙特卡洛法（精确解）基本吻合，且第25代左右已收敛，说明NGA计算复杂功能函数可靠度具有精度高、收敛速度快等优点.

4）通过工程算例验证了RBF-NGA的结果精度高、可靠性高等优点，故该算法具有一定的工程实际意义.

参考文献

[1]    SU G，PENG L，HU L. A Gaussian process-based dynamic surrogate model for complex engineering structural reliability analysis [J]. Structural Safety，2017，68：97—109.

[2]    AU S K，BECK J L. A new adaptive importance sampling scheme for reliability calculations[J]. Structural Safety，1999，21（2）：135—158.

[3]    CHAKRABORTY S，CHOWDHURY R. Assessment of polynomial correlated function expansion for high-fidelity structural reliability analysis[J]. Structural Safety，2016，59：9—19.

[4]    张杰，肖汝诚，程进. 基于神经网络的隐式显化方法在结构可靠度分析中的应用[J]. 力学季刊，2007，28（1）：135—141.

ZHANG J，XIAO R C，CHENG J. An explicit method based on implicit expression of neural network for structure reliability application[J] Chinese Quarterly of Mechanics，2007，28（1）：135—141. （In Chinese）

[5]    周道成，段忠东，欧进萍. 具有隐式功能函数的结构可靠指标计算的改进矩法[J]. 东南大学学报（自然科学版），2005，35（S1）：139—143.

ZHOU D C，DUAN Z D，OU J P. Improved moment method for reliability index without explicit performance function[J]. Journal of Southeastern University （Natural Science），2005，35（S1）：139—143. （In Chinese）

[6]    張建仁，刘扬. 遗传算法和人工神经网络在斜拉桥可靠度分析中的应用[J]. 土木工程学报，2001，34（1）：7—13.

ZHANG J R，LIU Y. Reliability analysis of cable-stayed bridge using GAS and ANN[J]. China Civil Engineering Journal，2001，34（1）：7—13. （In Chinese）

[7]    周芬，郭奥飞，杜运兴. 边坡稳定可靠度分析的新型四阶矩法[J]. 湖南大学学报（自然科学版），2016，43（5）：113—119.

ZHOU F，GUO A F，DU Y X. A new method of four order moments for reliability analysis on slope stability[J]. Journal of Hunan University（Natural Sciences），2016，43（5）：113—119. （In Chinese）

[8]    刘扬，鲁乃唯，殷新锋. 基于体系可靠度的钢桁梁结构优化设计[J]. 中南大学学报（自然科学版），2014，45（10）：3629—3636.

LIU Y，LU N W，YIN X F. Structural optimization design of steel truss beam based on system reliability[J]. Journal of Central South University （Science and Technology），2014，45（10）：3629—3636. （In Chinese）

[9]    郑敏，梁枢果，熊铁华，等. 基于可靠度的输电塔抗风优化研究[J]. 湖南大学学报（自然科学版），2014，41（6）：35—42.

ZHEN M，LIANG S G，XIONG T H，et al. Study on the reliability-based wind resistant optimization of transmission line tower[J]. Journal of Hunan University （Natural Sciences），2014，41（6）：35—42. （In Chinese）

[10]  HAI A，AN W，YANG D. Static force reliability analysis of truss structure with piezoelectric patches affixed to its surface[J]. Chinese Journal of Aeronautics，2009，22（1）：22—31.

[11]  范文亮，周擎宇，李正良. 基于單变量降维模型和坐标旋转的可靠度混合分析方法[J]. 土木工程学报，2017，50（5）：12—18.

FAN W L，ZHOU Q Y，LI Z L. Hybrid reliability method based on the univariate dimension-reduction method and rotational transformation of variables[J]. China Civil Engineering Journal，2017，50（5）：12—18. （In Chinese）

[12]  方开泰. 均匀设计与均匀设计表1[M]. 北京：科学出版社，1994：151.

FANG K T. Uniform design and uniform design table[M]. Beijing：Science Press，1994：151. （In Chinese）

[13]  TANG Q Y，ZHANG C X. Data processing system （DPS） software with experimental design，statistical analysis and data mining developed for use in entomological research[J]. Insect Science，2013，20（2）：254—260.

[14]  赵国藩. 结构可靠度理论[M]. 北京：中国建筑工业出版社，2000：12—34.

ZHAO G F. Structural reliability theory[M]. Beijing：China Architecture & Building Press，2000：12—34. （In Chinese）