拉索失效对多重四边环索-张弦穹顶的影响

张超　付馨迪　许莉　颜学渊　贾宏宇

摘   要：多重四邊环索-张弦穹顶结构作为一种新型的索支穹顶结构，拉索失效会对屋盖结构受力产生较大影响. 以全国首座三重四边环索-张弦穹顶屋盖（福州海峡奥林匹克中心体育馆屋盖）为研究背景，研究了拉索失效对于此类新型索支穹顶结构的竖向刚度、构件内力及极限承载能力的影响规律，并评估单根拉索失效后屋盖结构的安全性. 分析结果表1明：拉索失效均会引起屋盖显著下挠，各种工况中外环索失效会引起最大的屋盖下挠，但是，不同拉索失效后屋盖竖向变形分布规律相差较大;外环索和张弦索的失效会引起相邻拉索索力不同程度的增大;外环索与张弦索的相互影响大于各环索之间的相互影响;不同位置的拉索失效均会引起屋盖极限承载能力下降，外环索失效引起结构极限承载力下降最显著;“仅单侧张弦索失效”会引起较“两侧张弦索均失效”更不利的屋盖挠度和极限承载力. 总之，外环索失效为最不利拉索失效工况，会引起屋盖最大挠度增大134%，张弦索索力增加11.7%，极限承载力减小35%. 但是，剩余整体屋盖结构仍具有一定的安全性.

关键词：多重环索;张弦梁;穹顶;拉索失效;极限承载能力

中图分类号：TU356                       文献标志码：A

Influence of Multiple Square Loops-string Dome Subjected to Cable Failure

ZHANG Chao1，2，FU Xindi1，XU Li1，YAN Xueyuan1？，JIA Hongyu3

（1. College of Civil Engineering，Fuzhou University，Fuzhou 350108，China;

2. Key Laboratory of Urban Security & Disaster Engineering （Beijing University of Technology） of the MOE，Beijing 100124，China;

3. School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China）

Abstract：Multiple square loops-string dome is a newly suspen-dome structure，and cable failure shows significant effect on multiple square loops-string dome structures. This paper used the Fuzhou Strait Olympic Center Gymnasium as the research background to study the effect of cable on the vertical stiffness of the roof，the internal forces of the roof and the ultimate bearing capacity，and safety capability evaluation of the cable failure roof was carried out. The analysis results show that the vertical deformation of the roof can be reduced after cable failure. Among them，the failure of the outer loop cable causes the maximum vertical deformation. However，various vertical deformation distributions subjected to different cable failure are generated. The failure of either the outer loop or string cable can increase the tension force of the adjacent cable significantly. The interaction between the outer loop cable and string cable is greater than the mutual influence between the other loop cables; Ultimate bearing capacity of the roof can be reduced when cable failure occurs，which reaches the minimum value when the outer loop cable fails. It should be noted that “Only one side string cable failure” causes more serious deflection and less ultimate bearing capacity when compared with“two side string cable failure”. In all，failure of the outer loop cable is the most serious case，which causes that vertical deflection increases by 134%，the cable tension force of adjacent cable increases by 11.7%，and the ultimate bearing capacity reduces by 35%. However，the residual roof structure is still in a safe state.

Key words：multiple square loops;beam string;domes;cable failure;ultimate bearing capacity

弦支穹顶结构是由日本政法大学川口卫教授于1993年提出的一种新型杂交空间结构[1]，具有造型美观、节省材料、质量轻、刚度大、抗震性能好等空间结构的综合优势，在大型的公共与工业建筑中得到广泛应用. 典型的工程应用包括日本前桥绿色会馆、日本北九州穴生屋顶、济南奥体中心体育馆、常州体育馆、2008年北京奥运会羽毛球馆等.

1963年1月，罗马尼亚布加勒斯特市一座直径为93 m的国家经济展览馆穹顶网壳在近1 m厚积雪作用下失稳倒塌. 此后，网壳结构的安全问题成为人们研究的热点. 索结构属于柔性结构体系，预应力的引入可显著改善网格结构的整体变形、杆件内力峰值和整体稳定承载力[2].虽然在索穹顶结构设计中，拉索的设计应力只取索强度的30%～50%，且均采用强度较高的钢材，不容易发生破断，但实际使用过程中依然会因材料质量缺陷、维护缺陷、加工和施工缺陷等偶然因素引起某根索的破断，造成结构整体性垮塌.

对于预应力索杆结构的断索安全性，国内外学者已开展了相关研究，如索穹顶[3]、张拉整体[4]、张弦桁架[5]、弦支穹顶[6-9]、索杆结构[10-13]等. 朱明亮等[7]对一种由周边环形张拉整体和中部索穹顶组成的新型环箍-穹顶全张力结构进行静力和动力分析，发现张拉整体单元的拉索破断主要影响所在单元附近拉索，不会形成连续倒塌. 姜正荣等[12]对Levy型索穹顶结构索杆破断进行敏感性分析，发现Levy型索穹顶对环索和中心撑杆的破断最为敏感，其中最外环圈环索破断对应的敏感性系数最大. 高占远等[13]运用瞬态动力学的Newmark时间积分法对单根索杆断裂后结构的力学性能进行分析，并提出一种杆件重要系数，发现外环杆的重要性排在首位，内脊索排在末位. 然而，目前对于拉索失效影响的分析仅是针对传统弦支穹顶结构，由多重四边环索、张弦索组合形成的复杂弦支穹顶屋盖，各重拉索体系的受力相互影响，某局部拉索失效后，剩余拉索体系（同一环索中剩余拉索及其他重环索）会进行复杂的内力重分布，对于屋盖结构的影响规律可能会显著区别于传统索穹顶结构. 因此，本文以全国首个三重四边环索-张弦索组合穹顶屋盖——福州海峡奥林匹克中心体育馆工程为研究背景，研究可能发生的拉索失效对于此类新型索支穹顶屋盖结构的刚度、内力、稳定极限承载能力的影响规律，并评估单根拉索断裂后屋盖结构的安全性.

1   工程背景及数值模型

1.1   工程背景

福州海峡奥林匹克中心体育馆屋盖采用多重四边环索-张弦穹顶结构，由网格梁、撑杆、斜索、四边形环索、张弦梁构成，其中各层撑杆与网格梁和索的连接均为铰接. 屋盖跨度约97 m × 116 m，周围混凝土柱作为屋盖结构的内支座，弦支结构网格梁与支座刚接，网格梁采用矩形截面钢管. 为保证屋盖结构的空间几何稳定性，并避免压杆侧向失稳，本结构在网格梁中设置十字交叉形和V形两种形式的屋面支撑，采用圆形截面钢管. 屋盖网格梁、撑杆、支撑等型钢构件均采用Q345，混凝土柱采用C40. 此屋盖结构东西方向对称，北侧屋盖标高高于南侧，且北侧网格梁横向跨度略大于南侧网格梁.

三重四边环索成矩形，第一环（内环）撑杆高度9.0 m，四边形环索长21.6 m、19.0 m，斜索长13.9 m、15.0 m;第二环（中环）撑杆9.0 m，四边形环索长37.9 m、36.0 m，斜索长13.4 m、14.85 m;第三环（外环）撑杆9.5 m，四边形环索长56.9 m、51.1 m，斜索长度15.8 m、18.2 m. 为增加竖向刚度，在四边形环索第三环增设中间撑杆，高13.0 m，在东西两侧设置独立张弦结构，撑杆高度8.5 m、11.0 m，索规格及相关参数见表11.

1.2   三维数值模型建立

本文采用SAP2000建立三维空间数值模型，如图1所示. 其中，网格梁为箱型截面，屋面支撑为圆形截面钢管，均采用Frame单元模拟，钢材弹性模量为206 GPa;预应力拉索采用Cable单元模拟，拉索弹性模量为195 GPa. “型钢混凝土环梁”和“混凝土柱”均采用Frame单元模拟，截面特性均按照实际截面计算;根据环梁与混凝土柱刚接的实际情况，数值模型中，混凝土柱顶节点与环梁节点刚接;混凝土柱底则为固端约束.

（c）屋盖变形监测节点

图2   关键构件编号示意图

Fig.2   Numbering diagram of key components

1.3   基准数值模型验证

為验证本文所建数值模型的准确性，按实际屋盖施工过程中拉索张拉情况，定义非线性阶段施工工况，采用短链杆的温降收缩[14]模拟索力张拉过程，得到不同索力张拉过程中各监测关键点的受力及变形. 监测关键点布置情况如图3（a）、图4（a）所示.

图3（b）、图4（b）分别表1示网格梁应力和屋盖节点挠度的实测数据与模型计算结果的对比. 从图3（b）中可看出，实测数据与模型计算结果相差较小，误差最大的为16号，实测数据与模型计算值相差16.1 MPa. 从图4（b）中可看出，实测数据的挠度值略小于模型计算值，但两者相差较小，误差最大的为6号节点，二者相差10.1 mm. 由于篇幅有限，其监测结果对比详见文献[15].

总之，各施工阶段的数值模拟结果与实际施工监测数据总体吻合较好，误差均在可接受的范围内. 因此，本文在后续分析中，以此数值模型为基准分析模型.

2   完整屋盖结构的响应规律

2.1   变形及内力响应

在上节基准数值模型的基础上，健康状态下的完整屋盖结构（后文简称“完整屋盖”，以区分于拉索失效后屋盖结构）在实际运营过程中，应考虑屋面盖板等二期附加恒载以及屋盖活荷载的组合作用，其中，附加恒载为0.823 kN/m2，活载为0.5 kN/m2. 本文按“1.0附加恒载+1.0活载”考虑正常使用阶段的荷载组合.

在正常使用阶段荷载组合作用下，完整屋盖的变形和轴向应力如图5、图6所示，其中跨中节点位移最大，达106 mm，小于规范[16]规定屋盖跨中挠度控制值388 mm （L/250，L为完整屋盖短跨）. 外环斜索附近屋面支撑的压应力最大，约为127 MPa，但小于Q345钢材的抗压强度设计值f （310 MPa）.

竖向撑杆可看作是两端铰接的轴心受压构件. 本屋盖体系中各类型撑杆轴压力及截面应力见表12. 根据《钢结构设计规范》[16]需要对受压构件进行强度承载力和稳定承载力验算. 根据稳定承载力验算，截面应力应小于φf. 其中，f为钢材的轴心受压强度，设计值为310 MPa;φ为轴压构件稳定系数，根据构件的长细比、钢材屈服强度和截面分类按规范[16]中附录C采用. 稳定性验算结果见表13，所有竖向撑杆的稳定承载力满足设计要求，并有一定的富余度.

表13、表14分别为各个位置的水平拉索及斜索索力分布. 可以看出：各重环的索力分布基本呈对称状

态，南北向的索力均大于东西向的索力;同一重环的斜索索力大于环索索力;索力从内环到外环依次增大，水平索中，H34索力最大，达到3 192 kN，小于其对应的破断荷载（13 412 kN）;斜索中，X34索力最大，达到4 348 kN，远小于其对应的破断荷载（216 58 kN）.

2.2   极限承载能力

一般认为，弦支穹顶结构中的单层网壳属于缺陷敏感性结构，其临界荷载可能会因极小的初始几何缺陷而大大降低. 同时，文献[17]发现单层蜂窝型球面网壳因受到初始缺陷影响，其极限承载力不断下降. 因此本文采用一致缺陷模态法[18]来考虑屋盖的初始缺陷. 其中，初始缺陷按第一阶整体线性屈曲模态分布方式（如图7所示），表1现为：沿南北向屋盖竖向对称振动，沿东西向屋盖竖向反对称振动. 缺陷最大值按屋盖短跨跨度（L）的1/300选取.

为探讨完整屋盖的极限承载力，本文在对完整屋盖施加初始缺陷后，进行考虑几何、材料双重非线性的弹塑性极限承载力分析. 在弹塑性数值模型中，网格梁两端设置弯矩铰，屋面支撑和竖向撑杆设置轴力铰来模拟材料非线性. 其中，以1#网格梁为例（见图2（c）），列出计算的弯矩铰的弯矩-曲率曲线如图8所示;计算得到的2#屋面支撑（见图2（c））轴力铰的力-位移曲线如图9所示. 图8和图9中，点B代

图10给出了完整屋盖的极限承载力-位移曲线，为对比材料非线性的影响，对结构在考虑初始缺陷基础上进行弹塑性分析的同时，还进行了仅考虑几何非线性的弹性分析[19]. 可看出：完整屋盖的弹性极限承载力为66.7 MN，弹塑性极限承载力为56.1 MN. 说明弹性极限承载力会过高地估计屋盖结构承载力. 因此，后文计算屋盖结构极限承载力时均考虑屋盖结构的几何、材料双重非线性因素的影响.

3   拉索失效后屋盖结构的响应规律

3.1   拉索失效分析工况研究

本文数值分析中，采用变换荷载路径法[20]模拟拉索失效，即基于完整屋盖结构的数值模型，通过“移除”相应的失效单元，得到拉索失效后的屋盖结构，进一步分析拉索失效后屋盖结构的变形响应、内力分布及极限承载力，进而评估拉索失效后屋盖结构的安全性. 因多根拉索同时失效的概率较低，故本文仅探讨单根拉索失效后屋盖结构的安全性.

由表13、表14可知，完整屋盖结构中，不同位置（内环、中环、外环、张弦）和不同布置形式（水平索和斜索）的拉索索力的绝对值差别较大. 因此，本文分析中探讨了失效拉索位置和布置形式对剩余结构响应的影响.

以外环索为例，不同位置和布置形式的拉索失效后，剩余拉索索力值见表15. 从表1中可看出：当外环中水平索或斜索失效后，外环中剩余拉索的索力仅50 kN左右（为拉索自重引起），说明同环中其余剩余拉索亦已失效. 即環索中任一拉索失效，会引起此环索整体（共8根拉索）全部失效. 因此，针对同一重环索，取任一拉索失效工况即可. 同样地，张弦索中水平索或斜索失效，也会导致张弦索体系（共3根拉索）失效. 因此，针对张弦索，选择任一拉索失效工况均可.

由于环索体系和张弦体系引起的失效拉索数量分别为8根和3根，数量相差较大. 为了更公平地比较“环索体系失效”和“张弦体系失效”对屋盖结构的影响，后文分析中增加“全部张弦索均失效”的分析工况，即“东、西两侧张弦索均失效”.

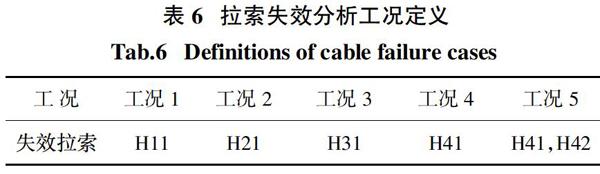
综上所述，针对此结构特点，本文拟定的拉索失效的5种工况，见表16.

图11所示为各重环索中水平索失效后的屋盖竖向变形云图. 可以看出：1）不同索失效后，引起不同程度的节点变形，从大到小依次为：工况3>工况4>工况1>工况2>工况5. 外环索失效的节点位移達到最大，为248 mm，为屋盖短跨L的1/391，小于变形限值（L/250）. 2）从变形云图上看，不同索失效的屋盖变形分布有较大差别. 为更细致地揭示不同拉索失效工况下屋盖变形规律，本文分别选取屋盖东西向和南北向关键节点的变形规律，如图12所示. 同时，为进一步研究拉索体系对屋盖结构竖向刚度的贡献，图12中还列出“仅上部网格梁屋盖结构”（后文简称为“无索屋盖”）的变形结果.

图12（a）所示为不同拉索失效工况下东西向关键节点的挠度分布图. 可以发现：工况1、2、3中跨中挠度最大，逐渐向两侧减小，挠度曲线呈“U”形，与完整屋盖和无索屋盖的变形曲线一致. 工况5中跨中挠度显著减小，东西两侧挠度增大，呈“W”形. 相比而言，工况4中西侧挠度显著增大，而东侧挠度减小，呈“√”形. 产生此变形差异的原因是：工况4中仅一侧张弦索失效后，另一侧张弦索仍正常工作，因此，剩余屋盖结构在东西向为不对称结构;对比而言，环索失效和两侧张弦梁失效后的剩余屋盖结构均为对称结构，因此，屋盖挠度曲线表1现为东西向对称.

另外，值得注意的是：1）工况1、2、3中靠近支座位置的竖向变形值反而较“完整屋盖”更小. 这是因为，存在诸多撑杆的东西向屋盖，可近似看成是“多点弹性支撑梁”. 当跨中挠度增大时，位于屋盖两端的节点则出现“变形反拱现象”. 2）工况4中屋盖最大挠度大于工况5中的屋盖最大挠度，这可能是因为工况4中未失效一侧张弦索产生的“反拱现象”加剧了失效一侧的张弦梁处屋面挠度.

图12（b）所示为不同拉索失效工况下南北向关键节点的挠度分布图，可以发现：

1）南北向“无索屋盖”挠度曲线表1现为北侧挠度大于南侧挠度，最大挠度位于节点JS4处;而“完整屋盖”挠度曲线表1现为对称状态，最大挠度位于跨中节点处. 导致两者变形曲线差异的原因是：结构网格梁屋盖的不等高设计，使“无索屋盖”在荷载作用下产生非对称变形. 而在“完整屋盖”中，即在“无索屋盖”的基础上增加拉索体系，从而改变屋面梁的竖向刚度，起到变形协调的作用.

2）工况1、4、5挠度曲线表1现为对称分布，工况2、3挠度曲线表1现为非对称分布. 产生这一现象的原因可以通过“完整屋盖”和“无索屋盖”的变形曲线比较得到解释：中环索、外环索失效（工况2、工况3），剩余索的预加力十分有限，导致剩余屋盖变形呈现类似“无索屋盖”的非对称变形特征. 而内环索失效（工况1），仅索力较小的内环索失效，剩余拉索预加力仍然很大，因此，其变形与“完整屋盖”更为接近.

值得一提的是，工况4、工况5中屋盖的跨中最大挠度小于完整屋盖. 此现象可由“变形反拱现象”得到解释.

3.3   拉索失效后的结构内力响应

图13所示为不同拉索失效工况下网格梁结构的轴向应力分布图. 从中可看出：不同断索工况下，外环斜索附近撑杆应力最大，且由大到小排列为：工况3>工况2>工况1>工况4>工况5. 其中，工况3，即外环索失效时，最大压应力达227 MPa，为完整屋盖的1.78倍.

表17列出了不同拉索失效工况下，剩余结构中关键拉索索力变化值. 从中可发现：

内环索（中环索）失效后（工况1、2），均不会引起剩余拉索索力的显著增加. 相反，还会引起外环索和张弦索的索力下降，此现象可从屋盖整体变形图得到解释（见图13）：当内环索（中环索）失效后，跨中挠度显著增大，相应地引起外环和张弦撑杆上端屋面梁产生“向上反拱”，最终，位于挠度反拱的网格梁下方的张弦索、外环索的索力下降.

外环索失效后（工况3），由于网格梁内力传递作用，与其距离较近的张弦索的内力增加约11.7%;但是，位于外环索内部的内环索和中环索的索力则有不同程度的下降，其中内环索索力下降近31.6%. 因此，屋盖变形图上表1现为跨中挠度高达-223 mm.

仅西侧张弦索失效时，与其相邻的外环索索力会略有增大，而中环、内环索及西侧张弦索的索力均减小;相比而言，当两侧张弦索均失效时，外环、中环、内环的索力变化规律与单侧拉索大致相同，但是变化数值约为后者的两倍.

综上所述，外环索和张弦索的失效会引起相邻拉索索力不同程度地显著增大，应引起重视;同时，外环索与张弦索的相互影响大于各环索之间的相互影响.

3.4   拉索失效后屋盖的弹塑性极限承载力

对拉索失效后屋盖结构进行考虑初始缺陷的双重非线性极限承载力分析. 图14给出了不同拉索失效工况下的屋盖在施加初始缺陷后考虑几何、材料双重非线性的极限承载力（以“完整屋盖的极限承载力”为基准来表1示），可以看出：拉索失效对剩余屋盖结构极限承载力产生的影响由大到小依次为：外环索、张弦索、中环索、内环索. 最不利工况为“外环索失效”：当外环索失效时（工况3），剩余屋盖极限承载力为36.2 MN，仅为完整屋盖的65%.

值得注意的是：单侧张弦索失效后剩余结构的极限承载力为36.9 MN，小于两侧张弦索失效后剩余结构的极限承载力（37.8 MN），说明单侧张弦索失效会引起极限承载力更显著的下降. 这一现象可以通过前文的“反拱现象”得以解释.

4   结   论

通过SAP2000模拟多重四边环索-张弦穹顶结构的拉索失效，得到以下结论：

1）作为一种新型结构，多重四边环索-张弦穹顶结构外圈环索对结构贡献最大. 外环索失效对结构节点位移、内力、极限承载力各响应的影响最大.

2）環索失效会引起整重环索失效，剩余结构仍为对称结构;张弦索失效仅引起单侧张弦索全部失效，剩余结构为非对称结构.

3）拉索失效后，经内力重分布会增大部分杆件的内力. 其中，外环索和张弦索的失效会引起相邻拉索索力不同程度地显著增大. 同时，外环索与张弦索的相互影响大于各环索之间的相互影响，应引起足够重视.

4）不同位置的拉索失效会引起极限承载力不同程度的下降，降幅由大到小依次为：工况3>工况4 >工况5>工况2>工况1.

5）“单侧张弦索失效”（3根拉索失效）引起的反拱现象，将导致“单侧张弦索失效”比“两侧张弦索失效工况（6根拉索失效）”，更为不利.

6）不管是四边环索体系，还是张弦索体系，均无多余的冗余度，为了提高此类结构的安全储备，建议采用一定的构造措施增加拉索体系冗余度.

参考文献

[1]    陈志华，刘红波，王小盾，等. 弦支穹顶结构研究综述[J]. 建筑结构学报，2010，31（S1）：210—215.

CHEN Z H，LIU H B，WANG X D，et al. Review and forecast of suspendome structures [J]. Journal of Building Structures，2010，31（S1）：210—215. （In Chinese）

[2]    贺拥军，孙轩，周绪红. 张弦巨型网格结构布索方案研究[J]. 湖南大学学报（自然科学版），2015，42（5）：8—13.

HE Y J，SUN X，ZHOU X H. Research on cable-strut arrangement of string reticulated mega-structure [J]. Journal of Hunan University （Natural Sciences），2015，42（5）：8—13. （In Chinese）

[3]    宗钟凌，郭正兴. 葵花型索穹顶结构力学性能及拉索破断试验研究[J]. 工程力学，2013，30（1）：271—276.

ZONG Z L，GUO Z X. Experimental research of mechanical properties and cable broken of levy cable dome [J]. Engineering Mechanics，2013，30（1）：271—276. （In Chinese）

[4]    SHEKASTENHBAND B，ABEDI K，DIANAT N，et al. Experimental and numerical studies on the collapse behavior of tensegrity systems considering cable rupture and strut collapse with snap-through [J].      International Journal of Non-linear Mechanics，2012，47（7）：751—768.

[5]    朱奕锋，冯健，蔡建国，等.  梅江会展中心张弦桁架抗连续倒塌分析[J]. 建筑结构学报，2013，34（3）：45—53.

ZHU Y F，FENG J，CAI J G，et al. Analysis on progressive collapse resistance of truss string structure of Meijiang Exhibition Center [J]. Journal of Building Structures，2013，34（3）：45—53. （In Chinese）

[6]    王化杰，范峰，钱宏亮，等. 巨型网格弦支穹顶预应力施工模拟分析与断索研究[J]. 建筑结构学报，2010，31（S1）：247—253.

WANG H J，FAN F，QIAN H L，et al. Analysis of pretensioning construction scheme and cable breaking for megastructure suspend-dome [J]. Journal of Building Structure，2010，31（S1）：247—253. （In Chinese）

[7]    朱明亮，陆金钰，郭正兴. 新型环箍穹顶全张力结构局部断索抗连续倒塌性能分析[J]. 东南大学学报（自然科学版），2016，46（5）：1057—1062.

ZHU M L，LU J Y，GUO Z X. Analysis on progressive collapse resistance of novel torus-dome tensile structure due to cable rupture [J]. Journal of Southeast University（Natural Science Edition），2016，46（5）：1057—1062. （In Chinese）

[8]    WANG X X，CHEN Z H，YU Y J，et al. Numerical and experimental study on loaded suspendome subjected to sudden cable failure [J]. Journal of Constructional Steel Research，2017，50（11）：358—371.

[9]    HAN Q H，LIU M J，LU Y，et al. Progressive collapse analysis of large-span reticulated domes [J]. International Journal of Steel Structures，2015，15（2）：261—269.

[10]  刘人杰，薛素铎，李雄彦，等. 环形交叉索桁结构局部断索（杆）的动力响应分析[J]. 工业建筑，2015，45（1）：32—35.

LIU R J，XUE S D，LI X Y，et al. Dynamic response analysis under local break of cable or rod in the annular crossed cable-truss structure [J]. Industrial Construction，2015，45（1）：32—35. （In Chinese）

[11]  陸金钰，董霄，李娜，等. 环箍-穹顶索杆结构局部断索抗倒塌能力分析[J]. 工程力学，2016，33（S1）：173—178.

LU J Y，DONG X，LI N，et al. Progressive collapse-resistant capacity analysis of torus-dome cable-strut structure due to cablerupture [J]. Engineering Mechanics，2016，33（S1）：173—178. （In Chinese）

[12]  姜正荣，刘小伟，石开荣，等. 索穹顶结构杆破断的敏感性分析[J]. 华南理工大学学报（自然科学版），2017，45（5）：90—96.

JIANG Z R，LIU X W，SHI K R，et al. Sensitivity analysis of cable-strut rupture for cable dome[J]. Journal of South China University of Technology（Natural Science Edition），2017，45（5）：90—96. （In Chinese）

[13]  高占远，薛素铎. 劲性支撑穹顶结构局部断索（杆）分析[J]. 四川大学学报（工程科学版），2017，49（5）：13—21.

GAO Z Y，XUE S D. Analysis of rigid bracing dome with broken cable（rod） [J]. Sichuan University （Advanced Engineering Science），2017，49（5）：13—21. （In Chinese）

[14]  张超，余立，许莉，等. 多重四边环索-张弦穹顶屋盖索力张拉方案比选[J]. 福州大学学报（自然科学版），2017，45（2）：151-158.

ZHANG C，YU L，XU L，et al. Comparative analysis on cable tensioning scheme of multiple square loops-string dome [J]. Journal of Fuzhou University （Natural Science Edition），2017，45（2）：151—158. （In Chinese）

[15]  张超，余立，刘涛. 多重四边形环索-张弦梁屋盖拉索张拉施工过程监测及数值模拟分析[J]. 武汉理工大学学报（交通科学与工程版），2016，40（5）：797—802.

ZHANG C，YU L，LIU T. Construction process monitoring and numerical simulation analysis of tensioning of multiple square loops-string dome [J]. Journal of Wuhan University of Technology （Transportation Science and Engineering），2016，40（5）：797—802. （In Chinese）

[16]  GB 50017—2003   钢结构设计规范[S]. 北京：中国建筑工业出版社，2003：29-47.

GB 50017—2003   Code for steel structures [S]. Beijing：China Architecture and Building Press，2003：29—47. （In Chinese）

[17]  贺拥军，彭正群. 蜂窝网格型球面网壳的非线性稳定性研究[J]. 湖南大学学报（自然科学版），2016，43（11）：33—38.

HE Y J，PENG Z Q. Nonlinear stability analysis of single-layer honeycomb spherical latticed shells [J]. Journal of Hunan University （Natural Sciences），2016，43（11）：33—38. （In Chinese）

[18]  HE S，JIANG Z，CAI J. Investigation on simulation methods of initial geometric imperfection distribution in elasto-plastic stability analysis of single-layer reticulated shells[J]. KSCE Journal of Civil Engineering，2018，22（4）：1193—1202.

[19]  崔曉强，郭彦林. Kiewit型弦支穹顶结构的弹性极限承载力研究[J]. 建筑结构学报，2003，24（1）：74—79.

CUI X Q，GUO Y L. Elastic ultimate capacity of Kiewitt suspen-dome [J]. Journal of Building Structures，2003，24（1）：74—79. （In Chinese）

[20]  KHUYEN H T，IWASAKI E. An approximate method of dynamic amplification factor for alternate load path in redundancy and progressive collapse linear static analysis for steel truss bridges [J]. Case Studies in Structural Engineering，2016，6：53—62.