基于模糊-层次法探讨临河承压水深基坑稳定与降水运营风险
2020-02-14陈湘贇
陶 俊,李 飞,张 飞,陈湘贇,李 戬
(1、苏州科技大学土木工程学院 江苏苏州215009;2、盐城工学院土木工程学院 江苏盐城224051)
0 引言
随着城市地下空间开发利用的不断发展,城市建设中的基坑工程逐渐向深基坑和大型基坑发展,受承压水影响的深基坑开挖稳定性问题成为了工程中的热点问题。特别是临河条件下,深大基坑开挖土体卸荷应力状态复杂[1],承压水减压降水运营[2]都容易产生较大地面沉降甚至稳定性破坏事故,造成严重的环境影响及人民生命财产损失。因此,临河条件下承压水深基坑开挖稳定性与降水运营风险源分析与评价已成工程中至关重要的问题。
1 风险评估方法
地下工程的风险评估始于20世纪末,国内外专家学者对基坑工程中的开挖施工风险与减压降水风险[3]等因素,提出了基于风险接受准则、可信性与可靠度等[4,5]的风险分析方法,总结分析了深基坑开挖与承压水降水等风险分析因素及其评价方法,为工程实践提供了良好的指导。基坑风险分析包括层次分析法[6]与模糊分析法[7]。本文根据临河承压水深基坑稳定与降水运营风险分析等问题,考虑了临河条件对基坑的影响,并增加了施工管理和周边环境等必要的风险源因素,通过层次分析法进行确定低层次风险源因素相对高层次的权重,同时,由于深基坑工程风险源的不确定性和模糊性的分布特点,利用模糊数学理论建立风险综合评判模型,可以为临河承压水深基坑稳定与降水运营的风险控制提供指导,从最大程度上确保基坑施工的安全。
2 层次分析法模型的建立
2.1 构建风险源层次结构图
笔者所在研究小组结合相关研究与文献,梳理归纳出临河承压水深基坑比较突出且具有代表性的风险因素,将它们由高到低分为目标层,中间层和决策指标层3 层次,并根据各层次风险因素绘制递阶层次结构图,如图1所示。
2.2 风险分析
2.2.1 比较判断矩阵的构造
针对盐城某临河承压水深基坑,在基坑施工前,向建筑类高校,设计单位,施工单位从事基坑工程研究或有施工、设计经验的专家发出调查问卷,邀请专家利用1~9 标度法对风险源因素之间的相对重要度通过两两比较进行量化打分,最后由专家综合所有的问卷商讨形成统一的打分,而为了对各层次每个风险源因素做出精确的综合判断,就需要构建判断矩阵[8]来表征它们之间的的重要性对比关系,从而确定它们的权重,1~9 标度是指两因素重要程度比较的量化估值,含义如表1所示。
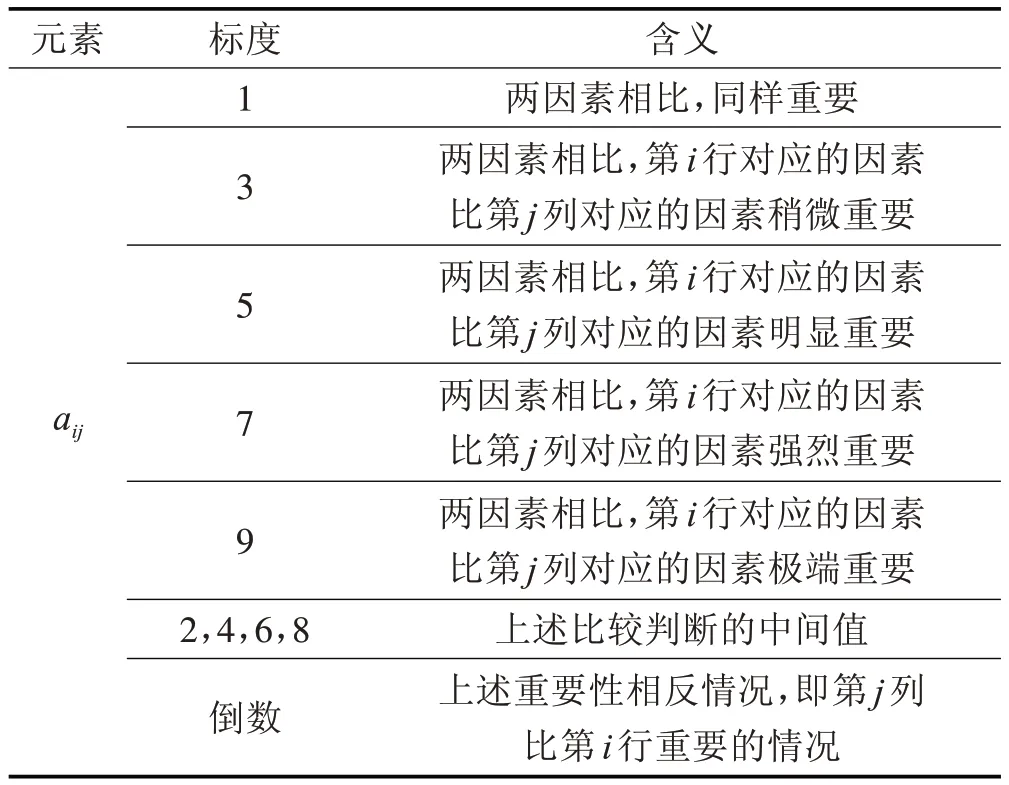
表1 1~9标度的含义Tab.1 Meaning of 1 to 9 Scale
2.2.2 评价因素权重的确定
为了防止主观判断失误,对构造的判断矩阵应检验其一致性,引入一致性比例CR,需满足CR<0.1,检验公式为CR=CI/RI,其中CI为一致性指标,RI为判断矩阵的平均随机性指标,如果不满足要求,需要请专家对各风险源相对重要性关系做出调整,直到构造的判断矩阵一致性检验通过为止。满足要求后,判断矩阵的最大特征值对应的特征向量就代表该层次每个风险源因子相对上一层次的权重向量。其中中间层各风险源因素的比较判断矩阵及一致性检验结果如表2所示。
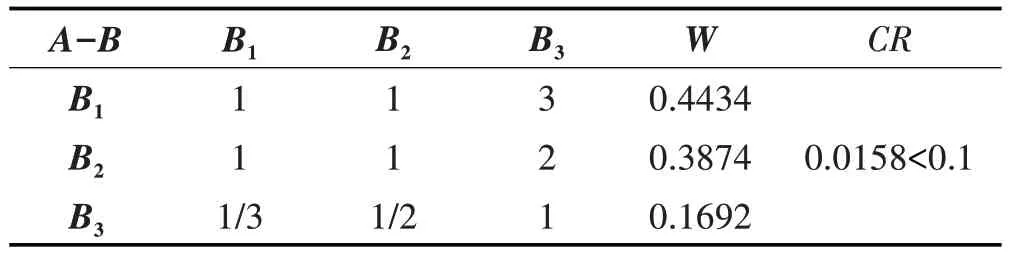
表2 A-B判断矩阵Tab.2 The A-B Judgment Matrix
从表2 中可以看出,对于A-B判断矩阵,计算出的一致性比例CR小于0.1,一致性满足求。
同理对中间层与决策指标层风险源构造的判断矩阵进行一致性检验,B1-C、B2-C、B3-C的一致性比例CR分别为0.063 1,0.085 2,0.076 7,可以看出一致性比例CR均小于0.1,一致性检验都满足要求。因此分别得到低层次风险源相对上一层次的权重向量。
施工与管理阶段各风险源的权重向量
ω1=(0.0551,0.0494,0.0901,0.3494,0.1437,0.3123)降水运行阶段各风险源的权重向量
ω2=(0.0562,0.1740,0.1287,0.2365,0.2880,0.1166)
环境因素影响中各风险源的权重向量
ω3=(0.1722,0.1750,0.0860,0.3288,0.2380)
中间层风险源相对目标层的权重向量
W=(0.4434,0.3874,0.1692)
而对于最低层次中各风险源因素相对于最高层次的综合权重需要通过中间层因素的权重与对应的决策层因素的权重相乘得到,为防止判断矩阵一致性差异的累加导致一致性比例不满足要求,还需要进行总体的一致性检验,检验公式为:

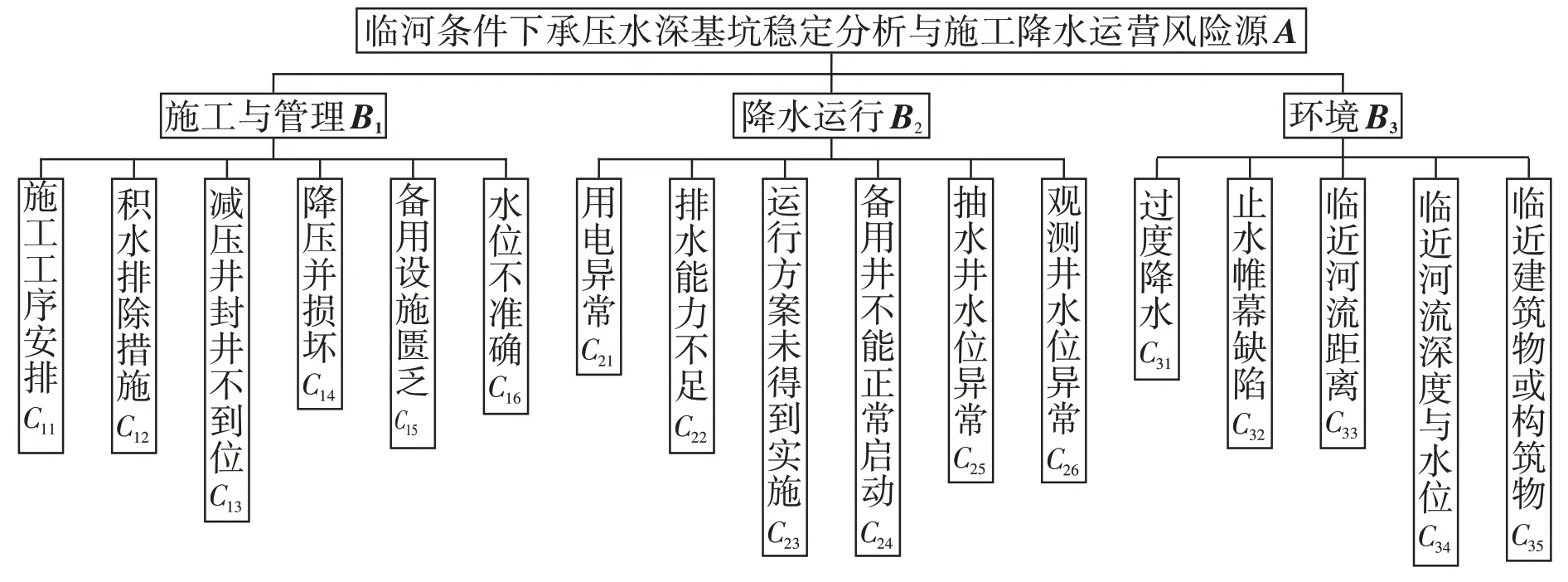
图1 临河承压水深基坑稳定性与施工降水运营风险源分析递阶层次结构图Fig.1 Hierarchical Structure Diagram of Analysis of Stability and Risk Sources of Construction Dewatering Operation of Deep Near-river Excavation with Confined Water
可以看出总体一致性检验满足要求,说明所有判断矩阵是具有完全一致性的,最后将每个决策指标层的风险源因素按综合权重排序,结果如表3所示。

表3 风险源综合权重及总排序结果Tab.3 Comprehensive Weight of Risk Sources and Total Ranking Results
2.2.3 层次分析法结果分析
⑴ 从表3可知,中间层风险源相对目标层的权重向量为W=(0.443 4,0.387 4,0.169 2),表明:对于该承压水深基坑稳定性与施工降水运营风险中,3 个中间层风险因素重要程度按从大到小顺序排列依次为施工与管理,降水运行,环境,说明施工管理和降水运行过程中的风险最重要,另外环境因素也不能忽视。
⑵ 表3 按综合权重对各决策指标层风险因素的重要性进行排序,可直观地看出降压井损坏和水位不准确等降水有关的风险对承压水深基坑工程最重要,需要引起重视。
3 模糊综合评判模型的建立
3.1 确定风险源因素集
结合图1 建立的各层次风险源层次结构图,可以构造因素集为U={B1,B2,B3},各因素子集为B1={C11,C12,C13,C14,C15,C16},B2={C21,C22,C23,C24,C25,C26},B3={C31,C32,C33,C34,C35}。
3.2 确定评判等级评语集
根据临河深基坑开挖与降水运营过程现场和风险发生案例的情况,可将其风险等级分为5个等级,设立评语集V={V1(一级),V2(二级),V3(三级),V4(四级),V5(五级)},结合临河深基坑工程风险承受能力和风险特征,建立相应的风险接受准则,如表4所示。
3.3 确定风险等级隶属度
3.3.1 风险的定义
基于可靠度的风险分析方法,风险指标采用风险发生的概率大小和造成的风险损失来度量,可以定义为:

式中:R为临河深基坑稳定与降水运营风险指标;P为风险源出现的概率;C为风险源造成的损失。

表4 风险等级评价量化表Tab.4 The Quantification of Risk Assessment Levels
3.3.2 风险指标的确定
首先通过专家调查法,同针对各层次风险源因素相对重要性打分类似,向近百位专家发出调查问卷,邀请他们依据深基坑领域的现场经验及专业知识,对决策层各具体风险因素发生的概率P及造成的影响后果C进行估值打分,估值方法如表5、表6所示。
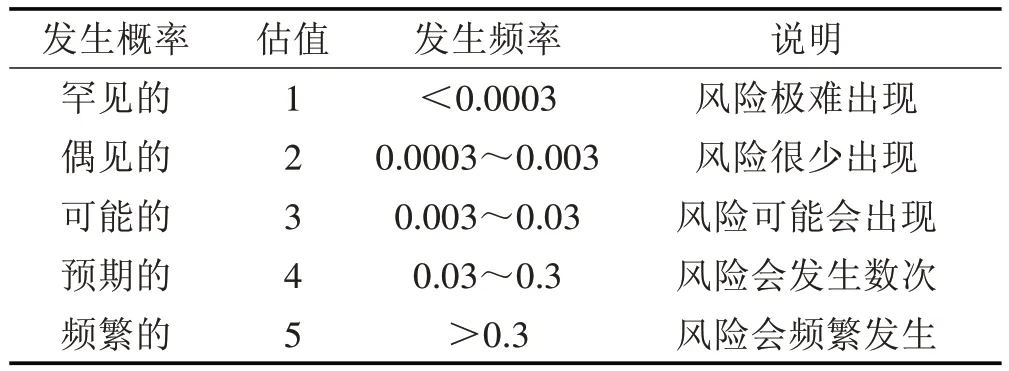
表5 风险源发生概率P的估值方法Tab.5 The Valuation Method of Risk Source Probability

表6 风险影响后果C的估值方法Tab.6 The Valuation Method of Rsk Impact Cnsequence C
在多位专家对同一风险源进行评估时,该风险源的发生概率和影响后果会出现不同的评估结果,为了使每个风险源得到一个综合评估结果,本文采用加权平均法[5],将各位专家根据其职称,经验,影响力等设立相应的权重,与他们对每个风险源发生概率和影响后果的估分结果进行加权运算得到P和C,最后进行风险指标的计算,计算结果如表7所示。

表7 专家评分统计表Tab.7 The Statistical Table of Expert Risk Value Assessment
3.4 确定隶属函数
隶属函数的确定方法是模糊数学的关键思想,在因素集参量与评语集之间需要引入适当的隶属函数,从而可以构造出隶属度的模糊集合。为了使风险评价更符合客观实际,本文依据其构造方法和原则[9,10],选取指派法中的二次抛物线型分布作为隶属函数,各区间具体表达式和函数图如表8和图2所示。
3.5 确定单因素模糊评判矩阵
在模糊数学中,矩阵的每一行表示一个模糊子集,每一行构成该风险源因素对每个等级的隶属度rij的集合,将各模糊子集组合起来,就构成模糊关系矩阵。因此将P和C的乘积值作为未知量代入表8 所列的各隶属函数中,从而建立了各中间层风险源的模糊评判矩阵。结果如下:
3.5.1 施工与管理阶段风险形成的评判矩阵b1


表8 隶属函数表达式Tab.8 The Expression of the Member Ship Function
3.5.2 降水运行阶段风险形成的评判矩阵b2

3.5.3 环境因素影响中风险形成的评判矩阵b3

3.6 一级模糊综合评判
一级模糊评判是将决策指标层风险源相对中间层的权重向量与以上对应一级评判矩阵进行运算,令Si=(S1S2S3S4S5)为评价域V上一个模糊子集,各元素表示各风险源的对应评判等级的隶属度大小,则中间层风险源的隶属度向量可表示为:

式中:“○”表示模糊子集的合成运算,与实数矩阵的点积运算相同,可得到:

归一化结果为:

根据最大隶属度的方法[8],可知中间层各风险源隶属度向量中第3 个元素对应的隶属度数值最大,即施工与管理阶段风险,降水运营阶段风险,环境因素影响风险等级都属于三级。
3.7 二级模糊评判
将各中间层风险源的隶属度向量组成新的评判矩阵,与各中间层风险源相对目标层的权重向量进行模糊运算,可以得到临河承压水深基坑稳定和降水运营的总体风险等级,二级评判矩阵可表示为:

则二级模糊综合评判结果为:

根据最大隶属度原则,可以确定目标层风险源总体风险为三级风险。
4 结语
⑴ 该临河承压水深基坑稳定性与降水运营总体风险等级为中等水平,属于可接受风险,结合层次分析法发现,与减压降水有关的施工管理与运营尤其重要,因此在实际临河深基坑开挖中应确保降水设备的正常运营及水位的精确测量。
⑵ 在专家调查法运用中既发挥了专家经验的作用,又一定程度上通过确定权重向量前的一致性检验消除了基坑工程风险的随机性,使风险分析结果偏于精确。
⑶ 通过将层次分析法与模糊综合评判理论结合,不但克服了临河承压水深基坑风险指标难以量化的缺点,而且使评判结果更加层次分明,系统全面,更加符合工程实际。因此这种方法可以应用到类似基坑工程风险分析中,进而针对各级定量评判结果,可以通过风险接受准则采取相应的控制措施,将风险降低到最合理的程度。
