基于叶片光谱反射率的毛竹氮元素含量估测研究

林灵辰，余坤勇，曾 琪，姚 雄，邓洋波，范华栋，刘 健

（1.福建农林大学林学院，福建 福州 350002； 2.3S 技术与资源优化利用福建省高校重点实验室，福建 福州 350002）

毛竹是我国重要竹类树种，同时也是经济价值很高的笋、材两用竹种[1]，其广泛地分布于我国南方低山丘陵区[2]。根据我国第八次森林资源清查统计，中国毛竹面积已达430 万hm2，占所有竹林总面积的74%，在我国所有竹类资源中占有绝对优势[3]。氮元素是毛竹生长发育过程中的必要营养元素之一[4]，毛竹叶片中的氮元素含量在一定程度上能够反映毛竹生长状况以及毛竹林地土壤肥力，所以估测毛竹林氮元素含量对毛竹生长胁迫、氮元素缺乏情况、土壤肥力的间接估测等具有重要作用。

通过建立植被的生化参数与植被氮元素含量的模型进行反演是当前氮元素含量估测的主要方式，而光谱数据能够获取十分精细的植被信息，因此被广泛应用于植被氮元素含量的反演的研究中[5]，利用光谱数据对植物叶片生化组分进行快速、无损的监测已成为植物生长状况评价的重要内容[6]。1997年宫鹏和浦瑞良率先使用光谱数据完成了森林氮元素含量的反演[7]，随后薛红利[8]、Clark[9]、Mutang[10]等采用简单的逐步回归方法估测植被氮元素含量，其估测值与实测值具有相当高的相关性。邢东兴等[11]利用叶片原始反射率及其一阶导数光谱、一阶导数的对数光谱、二阶微分光谱等基于原始光谱的变换形式与果树叶片的全氮元素、全磷等含量的相关性进行分析从中选择最优的光谱数据形式构建逐步多元线性回归方程。随着研究的深入，有学者发现逐步多元线性回归方法存在过拟合[12]、参与波段的多重共线性且与生化组分无关[13]等问题。随机森林算法（RF）具有很强的抗过拟合能力，因而被广泛地运用于分类与回归分析中，李旭青 等[14]基于随机森林算法估测的水稻冠层氮元素含量研究结果表明随机森林算法具有普适性、不会过拟合等优点。支持向量机（SVM）方法是由Vapnik 基于内核统计理论于1995年提出，大量研究表明它可以很好地运用于非线性回归问题，梁亮等[15]基于一阶微分敏感波长采用差值、比值以及归一化的方法构建了12 种光谱指数以及常用的22种植被指数，以此为参数采用最小二乘支持向量机回归算法对小麦冠层氮元素含量进行估测，同时优选出最佳的植被指数。

毛竹氮元素含量对研究毛竹生长状况以及估测毛竹林地土壤肥力具有重要意义，因此探索如何快速并精准地获取毛竹氮元素含量具有重要意义。为此，基于毛竹叶片光谱反射率构建了3 种毛竹叶片氮元素含量估测模型，并从中筛选出毛竹叶片氮元素含量的最优估测模型，为土壤肥力的间接估测以及进一步深入研究基于冠层尺度光谱估测毛竹氮元素含量奠定基础。

1 研究区概况

试验点分布于福建省顺昌县大干镇的武坊村、土垄村、干山村、良坊村以及1 个乡林场。其 经 纬 度 位 置 为26°50′30″ ～26°58′0″N，117°33′30″～117°47′30″E（图1），属于中亚热带季风气候，气候温和、雨量充沛，年平均降水量约为1 752 mm，年平均日照数约为1 700 h，年平均气温为16.3℃，海拔范围在118 ～1 282 m 之间。研究区地处山区，森林资源、水利资源十分丰富。大干镇总面积20 942 hm2，森林覆盖率高达78.8%，其中毛竹面积3 533.33 hm2，占林业用地面积的21.41%。

图1 研究区采样点Fig.1 Sampling points in the study area

2 数据采集及处理

2.1 叶片光谱数据的采集与预处理

2017年7月8—24日在福建省顺昌县大干镇布设59 个半径为3.26 m 的样圆串，并在3 个样圆内各选取1 株生长良好的毛竹作为样本树，将样本树伐倒后摘取冠层的上中下3 层叶子各2 片，每片叶子在黑色背景下测量5 次其正面光谱，剔除异常值后将3 个样本树的光谱数据取均值作为样地实测光谱数据，采用ISI921VF-256 野外地物光谱辐射计测量进行光谱的测量，光谱范围为可见-近红外（380 ～1 080 nm），光谱分辨率约为4 nm。采用The Unscrambler X10.4 软件中的Savizky-Golay 卷积平滑算法对原始光谱进行预处理，并用Origin 9.0 软件对其进行线性插值，光谱间隔为1 nm。

2.2 叶片氮元素含量的测定

每个样圆串的样本树冠层的上中下三层共摘取6 袋叶子，装入信封中后放入烘箱中进行105 ℃ 杀青20 min，之后75 ℃恒温进行烘干，直到叶片样品恒质量为止。用粉碎机粉碎后过筛形成待测样品，取0.1 g 待测样，使用德国VARIO MAX 碳氮元素分析仪进行测定，其工作原理是将待测样品完全燃烧后测定样品的全氮、全碳含量，实验对同一样品进行3 次重复平行试验，取3 个数据中的2 个误差较小的值取均值作为叶片全氮元素的实测数据。共59 个样地的实测数据，剔除6 个异常样本后随机选取43 个样本作为建模集，10 个样本作为验证集。

2.3 模型变量的选取

大量研究表明一阶微分光谱能够降低环境因素对目标光谱反射率的影响[16]，在构建氮元素估测模型时可以作为一个重要的变量类型。光谱植被指数是依据目标地物的光谱特性将某几个波段利用数学方式组合成的光谱指数，其具有指示植物体内某种生化组分的情况、减少背景干扰和突出目标信息等作用[17]，在氮元素含量估算研究中，常见的光谱植被指数有光化学植被指数（Photochemical reflectance index，PRI）、比值植被指数（Ratio vegetation index，RVI）、归一化植被指数（Normalized vegetation index，NDVI）等，参考国内外学者的研究，共选取了25 种与氮元素相关的光谱植被指数（表1）与毛竹叶片氮元素含量进行相关性分析并筛选模型变量。

2.4 模型构建原理

2.4.1 多元线性模型

多元线性回归是使用多个自变量对因变量进行解释的回归方法[18]，利用多元逐步回归方法能够自动筛选与目标变量相关关系最大的自变量进入模型从而去除无关变量的优点[19]，逐步筛选与毛竹叶片氮元素含量最密切的参数构建模型。

2.4.2 随机森林

随机森林算法（RF）是Breiman 等于2001年提出一种机器学习算法[20],由多个单独决策回归树组成，其工作原理为：用boostrasp 算法有放回地从N 个原始数据袋中随机抽取n 个样本形成新的建模集，未抽到的样本作为预测集样本估计模型的性能。若原始数据集有P 个变量，则每个决策树的每个节点抽取mtry 个变量，一般mtry=P/3，并根据这些特征变量计算最佳的分裂方式并对节点进行分裂，在运行不断生成大量决策树直到达到预先设定的决定树数目从而达到回归分析的目的。

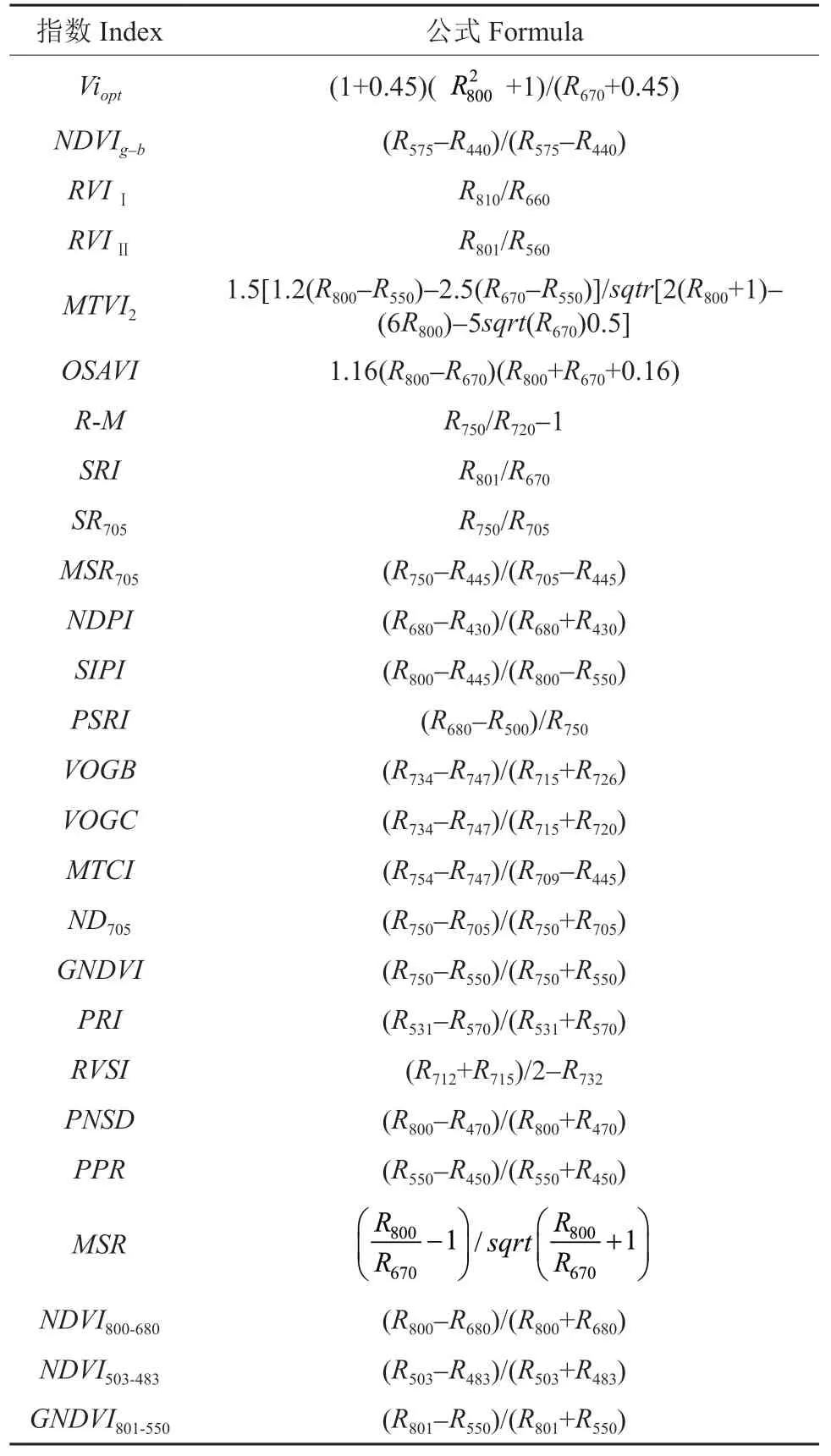
表1 选取的植被指数Table 1 Selected vegetation index

2.4.3 支持向量机

支持向量机（SVM）方法是由Vapnik 基于内核统计理论于1995年提出，其原理是通过一个非线性映射P 将样本空间映射到一个高维空间，并在这个空间将非线性可分问题转化为特征空间中的线性可分问题[21-23]，其实现关键在于核函数k(xi,xj)=φ( xi) ·φ(xj)，常见的核函数有4种：线性核函数、多项式核函数、径向基核函数、Sigmoid核函数。

3 结果与分析

3.1 不同氮元素含量的毛竹叶片光谱特征

氮元素对可见光和近红外波段不存在明显吸收、反射与透射特征，其敏感的吸收波段主要为短波红外，但是吸收特征相对较弱。氮元素的吸收特征主要是由于氮与叶绿素存在较强的相关关系，进而通过叶绿素的吸收特征进行表达[24]。图2 为毛竹不同氮含量的叶片光谱反射率。不同氮含量的毛竹叶片光谱反射率的规律具有很好的一致性，在可见光波段范围（380 ～760 nm）内，由于叶绿素的强反射有一绿色反射峰，在600 ～760 nm 的波段范围内，由于叶绿素强烈地吸收辐射能而形成吸收谷，其光谱反射率小于10%，约在680 ～760 nm 的波段范围，反射率急剧上升，在760 ～1 080 nm，形成一个高反射平台，该平台光谱反射率范围在40%～60%之间，随着氮含量的增加，此波段范围的反射率先降低后升高[25]。

图2 不同氮元素含量的毛竹叶片反射率光谱Fig.2 Reflectance spectra of leaves of moso bamboo with different nitrogen content

3.2 氮元素估测模型变量的选取

将毛竹叶片氮元素含量与原始光谱、一阶微分光谱进行相关性分析，结果如图3 所示，在原始光谱386 ～389 nm、394 ～396 nm 和411 ～415 nm的波段范围与氮元素含量处于极显著相关，其中在波长R387处相关性达到最大，相关系数为0.445 4，与一阶微分光谱的相关系数在380 ～1 080 nm 范围内的变化幅度比与原始光谱相关系数大，在波长385 nm、523 ～524 nm、600 ～601 nm、663 ～ 664 nm、666 nm、691 ～692 nm、773 nm、761 nm、 794 ～795 nm 处与叶片氮元素含量呈极显著相关，最大相关系数为0.490 0，对应波长为DR663。由于毛竹叶片氮元素含量与原始光谱、一阶微分光谱的相关性浮动较大，相关波长比较接近，因而选取R387、DR663作为构建氮元素估测模型的变量。

将毛竹叶片氮元素含量与25 种植被指数进行相关性分析，根据两者之间的相关性以及显著性进行敏感参数的选取，结果如表2，达到极显著相关的植被指数有归一化植被指数NDVIg-b(R575、R440)、结构不敏感色素SIPI、光化学反射指数PRI 和色素比值植被指数PPR，相关系数分别为 0.472 1、0.382 4、0.401 5 和0.380 3，故选取这4种植被指数作为变量进行模型的构建。

3.3 氮元素含量估测模型的构建

3.3.1 多元线性模型

将与毛竹叶片氮元素含量相关性较高的6 个敏感参数作为输入自变量，利用建模集中的43 个样本进行逐步回归拟合，结果如表2所示，模型共进入了DR663、PRI 2 个变量，模型方程为Y=0.333- 25.631*DR663-0.939*PRI，拟合系数R2为0.363。

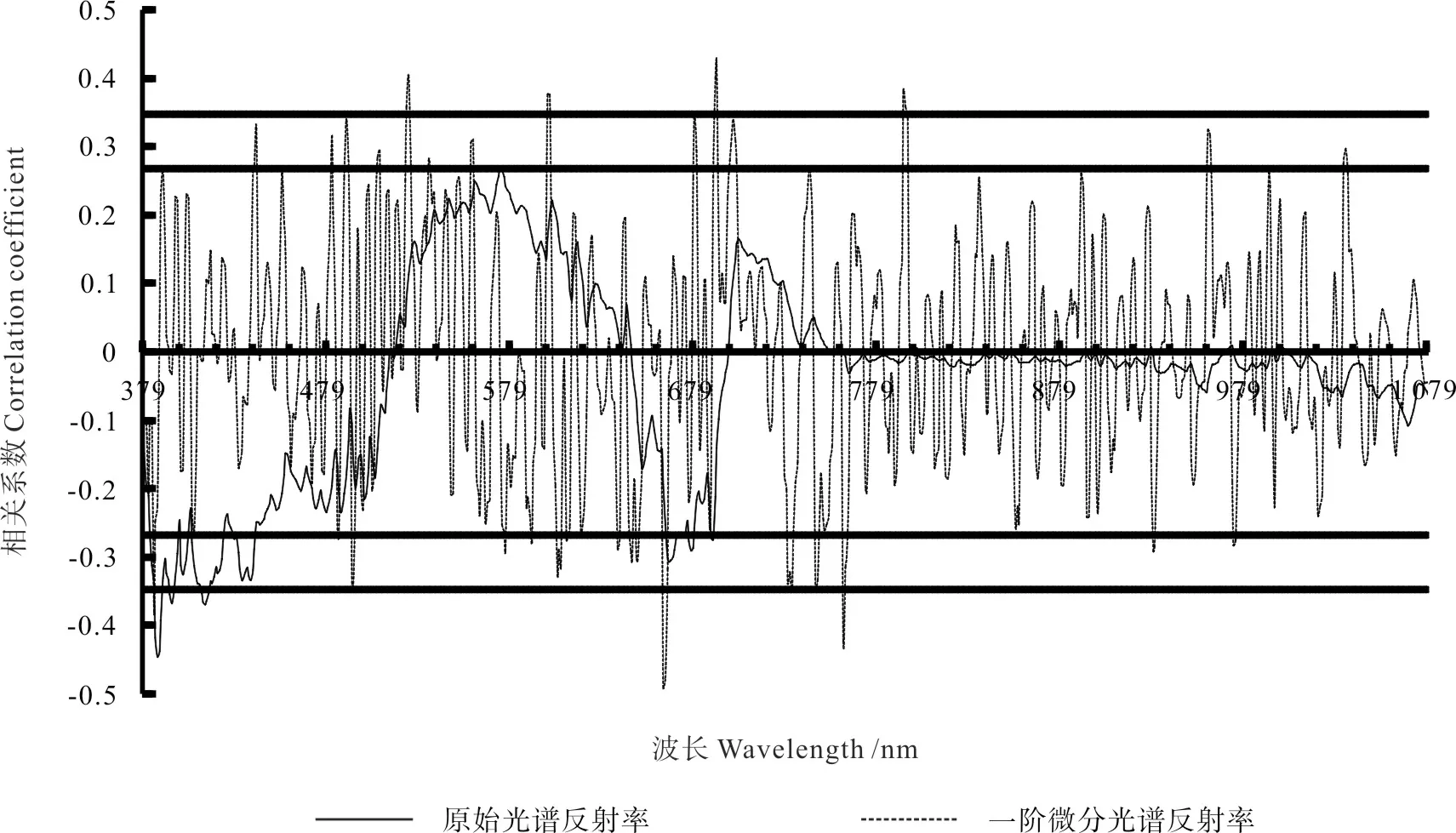
图3 毛竹叶片氮元素含量与叶片原始光谱、一阶微分光谱的相关性Fig.3 The correlation between leaf nitrogen content and leaf original spectrum and first-order differential spectrum of moso bamboo

3.3.2 非线性模型

为了保证随机森林模型以及支持向量机模型拟合得到的结果具有对比性，均采用筛选得到的6 个敏感参数组合作为随机森林和支持向量机的输入变量，同样利用建模集中的43 个样本进行拟合。随机森林的mtry 与决策树数量设置分别为2和1 000，从多次试验的结果中取得的随机森林最优拟合结果的拟合系数R2为0.353 2。SVM 算法采用径向基函数进行叶片氮元素含量估测模型的构建，经多次反复试验发现当惩罚因子C 和核参数Sigma 分别设置为3 和0.1 时的拟合效果最好，其估测结果的拟合系数R2达到了0.799 7。

表2 毛竹氮元素含量估测模型Table 2 Estimation model of nitrogen content in moso bamboo

3.4 模型精度检验分析

用验证集中的10 个样本对3 个模型进行精度检验，采用决定系数R2、均方根误差RMSE、预测偏差值bias 和总体平均精度来评价模型的估测能力。结果见图4，三个模型的估测值与实测值都在Y=X 附近波动，支持向量机的估测值与实测值的拟合度较高，而多元线性模型和随机森林模型的拟合点相对分散。从精度分析表3 可以看出，3 个估测模型的总体精度均达到了90%以上，其中支持向量机的R2是三个模型中最高的，达到了0.803 1，其预测偏差值与均方根误差相当小，综合均方根误差值、R2以及总体精度来看随机森林模型估测效果要略优于多元线性模型，二者与支持向量机模型估测结果相比效果较差。综合三个模型的精度检验结果来看，惩罚因子C 和核参数Sigma 分别设置为3 和0.1 的支持向量机模型的估测效果最佳。

4 结论与讨论

氮元素含量是影响毛竹生产的主要因素之一，同时也是反映毛竹生长状况的重要指标，因此研究如何快速获取毛竹氮元素含量具有重要意义，本研究利用地面实测光谱数据，从叶片角度探索毛竹林氮元素含量估测模型并取得了一定成果。

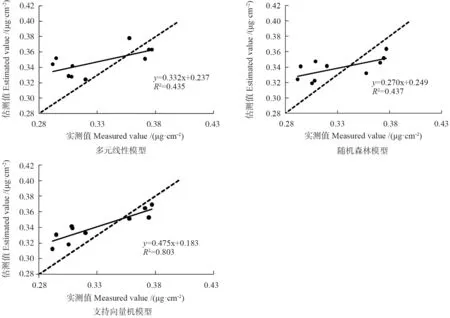
图4 模型精度比较Fig.4 Comparison of model accuracy

表3 精度分析Table 3 Precision analysis

1）结合毛竹叶片氮元素含量与叶片原始光谱、一阶微分光谱和植被指数三者之间的相关性分析结果发现：叶片原始光谱在波长387 nm 处相关性达到最大，一阶微分光谱在波长663 nm 处相关性达到最大，NDVIg-b、SIPI、PRI 和PPR4种植被指数与叶片氮元素含量达到极显著相关。可以看出与毛竹叶片氮元素含量达到极显著相关的原始光谱波段相对较少，这可能是因为在可见-近红外（380 ～1 080 nm）范围内其他生化组分的吸收波段与氮元素相近而产生干扰[26]，并且在实际的光谱操作过程中，不同的光谱分辨率、不同的光谱处理方法等也会对植被生化参数估测造成一定的影响。一阶微分光谱与氮元素含量达到极显著相关的波段远远多于原始光谱，这一结果与李哲等[27]、 丁雅等[28]的研究结果相一致，说明原始光谱的一阶微分变化形式在研究光谱与植被氮元素含量之间的关系时具有一定的优势。

2）利用6 个氮元素敏感特征参数作为输入变量构建毛竹氮元素含量多元线性估测模型、随机森林模型以及支持向量机模型，综合模型精度分析结果来看，支持向量机模型的R2、均方根误差、总体精度是3 个模型中最好的，这一结果与杨曦光[29]、李百超[30]的研究结果相一致。多元线性模型的决定系数以及整体精度略低于随机森林模型，但其预测偏差值过高，因此多元线性模型在用于估测毛竹氮元素含量时不具有优势，支持向量机模型在3 种模型中的估测结果效果是最好的，这与模型本身的特性有关，支持向量机在用于拟合样本较少的数据时具有更大优势[30]。

基于叶片光谱数据构建毛竹氮元素含量估测模型，对比精度检验结果发现支持向量机在估测叶片氮元素含量方面具有明显优势，其实测值与预测值的拟合系数与总体精度分别为0.803 1、94.02%，因此能够作为毛竹叶片氮元素含量的较佳估测方法。实验过程中存在几点不足，在之后的研究中将加以深化：可以增加多种原始光谱变化形式以及不同输入变量组合对毛竹氮元素含量的影响，同时增加样本数量来避免由于在实际光谱测量过程以及氮元素含量的测定过程中产生的实验误差而导致模型拟合精度下降的情况。