基于复杂渗流机理的页岩气藏压后数值模拟研究
2020-02-11陈祖华梅俊伟任建华
王 伟,李 阳,陈祖华,姚 军,梅俊伟,任建华,马 波
(1.中国石化华东油气分公司勘探开发研究院,江苏南京210011;2.中国石油化工股份有限公司,北京100728;3.中国石油大学(华东)石油工程学院,山东青岛266580)
随着世界能源需求的增加及油气开采技术的提高,非常规油气资源如煤层气、致密砂岩气、页岩油气等的开发日益受到重视,尤其是页岩气在美国、加拿大等国家已实现了商业化开采[1]。中国的页岩气资源量与美国相当,具有较大的开发潜力[2]。近几年中国川渝地区的页岩气勘探开发取得了重大突破[3-4],其中中国石化涪陵页岩气田进入了商业化开发阶段。中国页岩储集空间以纳米级孔隙为主[5],其孔隙度和渗透率非常低,且埋藏更深,地层压力更高[6-7],气体运移机制更复杂。
对于脆性较大的页岩储层,通常发育天然裂缝,实施水平井分段压裂改造措施之后,人工裂缝与天然裂缝相互沟通[8-9],这种页岩气藏进行物理模型简化时通常采用双重介质模型。相反,对于塑性较大的页岩储层,地层天然裂缝不发育,实施储层改造措施后,人工裂缝与天然裂缝沟通较差或不沟通,不容易形成缝网结构[10]。虽然基于连续介质模型的常规油藏数模软件计算效率高,但无法准确描述复杂裂缝网络渗流特征。而离散裂缝模型可以对大尺度裂缝进行显式处理,直接利用裂缝尺寸、裂缝位置、产状等属性参数,更加真实地描述裂缝的实际分布情况和储层的非均质特征。通过对裂缝进行降维处理,从而降低其网格划分复杂度和计算量。这种模型更适用于处理类似页岩气藏分段压裂水平井储层中多尺度裂缝和强非均质问题[11-17]。
结合真实气体性质、页岩气复杂渗流机理、裂缝系统应力敏感效应和人工裂缝非达西流动性质,利用离散裂缝模型表征天然裂缝和人工裂缝,建立了页岩气藏分段压裂水平井模型和复合气藏分段压裂水平井模型,并在平桥区块进行了应用。通过应用揭示出影响平桥区块页岩气井产量的主要因素,为后期井组、平台数值模拟及方案优化提供技术支持。
1 页岩气藏基岩运移机理
气体在页岩气藏基岩纳米孔隙中存在多种运移机制。不同组分气体分子与分子之间碰撞产生分子扩散,同种气体分子与分子之间碰撞产生黏性流,分子与壁面碰撞产生Knudsen扩散,吸附在孔隙壁面的气体分子沿孔隙表面蠕动产生表面扩散。当页岩气藏中仅存在单组份甲烷气体,且基岩中气体以游离态和吸附态共存时,页岩气藏基岩中气体运移是黏性流、Knudsen扩散和吸附层表面扩散共同作用的结果[18](图1)。
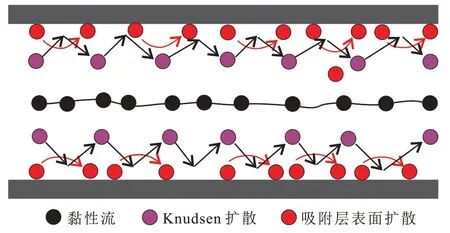
图1 单组分甲烷气体单管中运移机制Fig.1 Individual gas transport in porous media
1.1 黏性流
当气体平均运动自由程远小于孔隙直径时,气体分子的运动主要受分子间碰撞支配,分子与壁面的碰撞较少。此时在单组分气体之间存在压力梯度所引起的黏性流,黏性流的质量传输可以用达西定律表示[19]:

式中:Nv为黏性流流量,kg/(m2∙s);ρg为气体密度,kg/m3;k∞为多孔介质固有渗透率,m2;μg为气体黏度,Pa·s;P为孔隙压力,Pa。
1.2 Knudsen扩散
当孔隙直径很小时,气体的平均自由程与孔隙直径相近,这时气体分子与壁面之间的碰撞占支配作用,此时Knudsen扩散的质量流量可以表示为[20]:
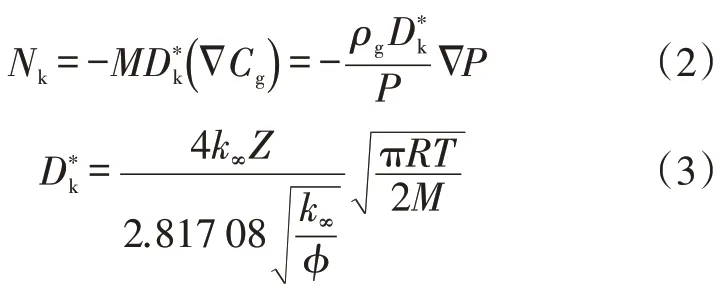
式中:Nk为Knudsen扩散流量,kg/(m2∙s);M为气体的摩尔质量,kg/mol为气体运移的有效Knudsen扩散系数,m2/s;Cg为气体浓度,mol/m3;Z为气体压缩因子;ϕ为多孔介质孔隙度;R为普适气体常数,J/(mol·k);T为气藏温度,K。
1.3 吸附气吸附/解吸
页岩气在基岩纳米孔隙表面的吸附气量遵循单分子层的Langmuir等温吸附规律[21]:
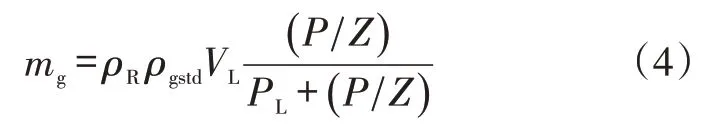
式中:mg为单位体积页岩内吸附的气体质量,kg/m3;ρR为基岩颗粒密度,kg/m3;ρgstd为标准状况下的气体密度,kg/m3;VL为Langmuir 体积,m3/kg;PL为Langmuir压力,Pa。
1.4 表面扩散
当页岩基岩孔隙内存在吸附气时,吸附在多孔介质表面的气体分子会沿着壁面发生运移,也就是吸附气沿着孔隙壁面产生表面扩散现象。气体的表面扩散可以用下式来描述[22]:

式中:Ns为表面扩散流量,kg/(m2·s);Ds为表面扩散系数,m2/s;Cμ为单位体积颗粒上的吸附气摩尔数,mol/m3。考虑气体Langmuir等温吸附规律,则有:

式中:Csmax为孔隙中的最大吸附浓度,mol/m3。
1.5 应力敏感效应
致密页岩储层中的天然裂缝是气体的主要运移通道,对页岩储层的渗透性影响很大。一些学者通过实验及理论研究证明页岩储层的渗透率随应力的变化而改变。天然裂缝渗透率随气藏压力变化关系可以利用幂律关系模型来表示[23],如下式:

式中:kf,stress为考虑应力敏感效应后的裂缝系统渗透率,m2;kf0为裂缝系统的固有渗透率,m2;df为应力敏感系数,1/Pa;pf为裂缝系统的压力,Pa;p0为初始压力,Pa。
2 页岩气藏压裂水平井数学模型建立及求解
2.1 基岩系统数学模型
基岩系统中同时含有游离气和吸附气,气体在基岩微纳米孔隙中的质量传输是由黏性流、Knudsen扩散、表面扩散以及气体的解吸共同作用的结果。根据质量守恒方程可得页岩气藏基岩中单相气体流动的连续性方程[24]:
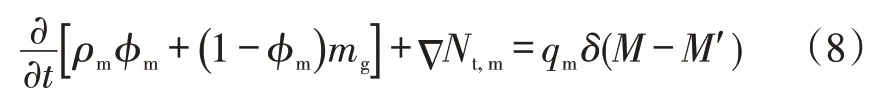
式中:Nt,m为基岩孔隙内气体的流量,kg/(m2·s),用式(9)表示;ρm为基岩孔隙内气体的密度,kg/m3;ϕm为基岩孔隙度;mg为吸附在单位体积岩石颗粒上的气体质量,kg/m3;qm为基岩处的源汇项,kg/s;δ(M-M')为delta 函数,当点M=M'时,δ(M-M')=1,其他情况下值等于0。

式中:km,app为考虑不同运移机制时的页岩基岩的视渗透率,m2;μgm为基岩孔隙内气体的黏度,Pa·s,pm为基岩系统孔隙内压力,Pa。基岩视渗透率表达式为:

考虑真实气体性质,将气体状态方程代入式(8)可得基岩系统的数学模型为:

定义Γ1为气藏的外边界,Γ2为基岩系统与天然裂缝系统的交界面,假设基岩系统与天然裂缝系统交界面上压力处处相等,则初始条件及边界条件为:
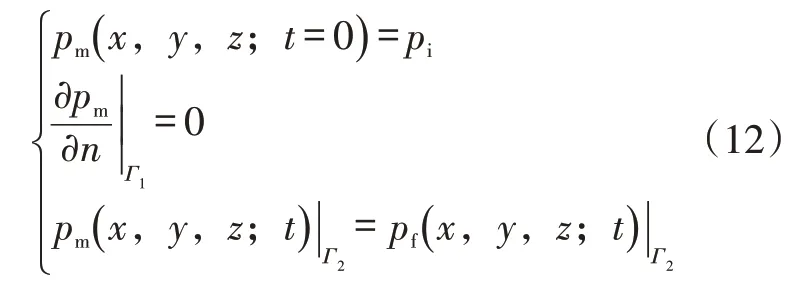
2.2 天然裂缝系统数学模型
页岩储层天然裂缝系统中仅存在游离气,气体运移机制为黏性流和Knudsen扩散,根据质量守恒方程可得页岩气藏天然裂缝系统中单相气体流动的连续性方程:
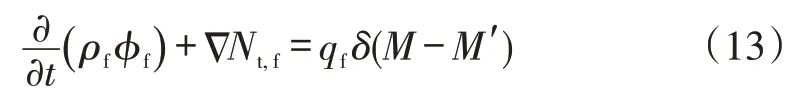
考虑天然裂缝系统的应力敏感效应及真实气体性质,将气体状态方程带入式(13)可得天然裂缝系统的数学模型:
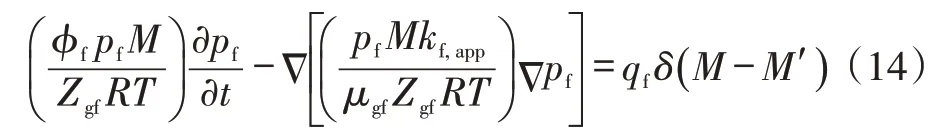
天然裂缝系统视渗透率表达式分别为:

定义Γ3为天然裂缝系统与人工裂缝系统的交界面,假设天然裂缝系统与人工裂缝系统交界处压力处处相等,则初始条件及边界条件为:

基于三维match—sticks 模型,天然裂缝系统的固有渗透率kf0和孔隙度ϕf的求取方式为:

式中:a为天然裂缝间距,m;b为天然裂缝开度,m。
2.3 人工裂缝系统数学模型
人工裂缝中仅存在游离气,开井生产后人工裂缝内压力迅速下降,压力梯度较高,气体黏度较低,气体在人工裂缝中的流动偏离达西流动,此时人工裂缝内气体的流速可以用Forchheimer 方程来表示。将气体状态方程、Forchheimer 方程及裂缝应力敏感性方程代入连续性方程,可得人工裂缝系统数学模型为:
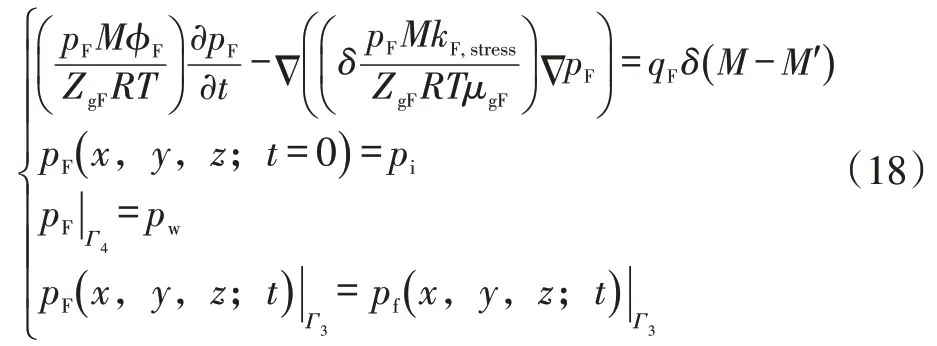
式中:Γ4表示水平井的内边界,模型中水平井定井底压力生产。
人工裂缝的固有渗透率kF可以采用立方定律求取:

式中:wF为人工裂缝开度,m。
2.4 模型求解
该文数学模型利用COMSOL Multiphysics多物理场仿真软件进行求解,天然裂缝和人工裂缝采用显式处理方式。显式处理裂缝可以有效刻画裂缝及周围基质流场剧烈变化的流动特征,常规显式处理方法将裂缝作为很小的高渗带处理,裂缝需要加密,网格量巨大,计算效率很低。该文使用离散裂缝模型(DFM)对天然裂缝和人工裂缝进行简化处理[25]。基于流量等效原理,将裂缝与基岩作为单重孔隙介质,对裂缝进行降维处理。在三维问题中可以将裂缝简化为二维的平面单元,二维问题中可以将裂缝简化为一维的线段,从而降低了网格划分难度,大大提高了计算效率(图2)。
二维气藏中,裂缝被近似为一条存在开度的线段,求解裂缝与基岩中流体的运动方程时,在裂缝积分前乘以裂缝开度以保证积分值相等,此时其积分形式可表示为:
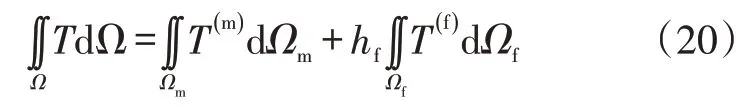
式中:Ω为整个气藏区域,Ωm和Ωf分别为基岩区域和裂缝区域,T代表运动方程。
3 实例计算及产量影响因素
利用平桥区块页岩气藏基本参数建立数值模型(表1)。为了便于模拟计算,选取页岩气藏分段压裂水平井中的一条人工裂缝作为一个研究单元。结合平桥区块水力压裂模拟和微地震监测结果,人工裂缝波及区域长度300 m,压裂段间距离75 m,人工裂缝纵向上高度50 m。模型内部既有基岩又有天然裂缝和人工裂缝。人工裂缝上下贯穿地层,沟通了天然裂缝系统,天然裂缝之间存在交叉,人工裂缝与部分天然裂缝沟通。
3.1 基础模型模拟结果
图3 给出了生产3 个月和12 个月后储层改造区域内压力分布图。由图3 可知,由于地层中存在大量的相互连通的天然裂缝系统,生产3 个月时压力降已经到达储层改造区域的外边界。生产12 个月后,由于人工裂缝与天然裂缝之间良好的沟通性,基岩中游离气和吸附气很快的流向裂缝系统,人工压裂裂缝穿透区域内的压力已经很低,储层改造区域内部大部分气体已经被采出。然而在人工压裂裂缝的尖端没有被沟通到的天然裂缝区域仍有大量的气体剩余。
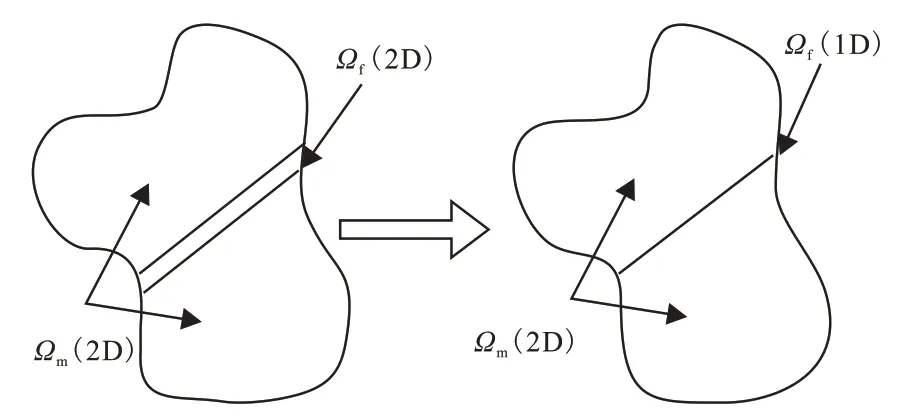
图2 离散裂缝模型降维Fig.2 Dimensionality reduction of discrete-fracture model

表1 页岩气藏压裂水平井数值模拟基本参数Table 1 Simulation parameters of fractured horizontal well in shale gas reservoir

图3 生产3个月和12个月后SRV单元内压力分布Fig.3 Pressure distribution in SRV after 3 and 12 months of production,respectively
网格内吸附气采出百分比=(原始吸附气含量-当前剩余吸附气量)/原始吸附气含量×100%,利用上述公式计算每个网格内吸附气采出百分比。图4给出了生产3 个月后SRV 区域内吸附气采出百分比分布。可知在生产早期吸附气采出程度非常低,平均只有10.1%,气井早期产量主要来自裂缝系统的游离气。只有裂缝壁面处的吸附气采出程度相对较高(最高为51.4%),但仍然有将近一半的吸附气残留在基岩中未能被采出。要想采出这部分残余气体,只能用更低的井底流压生产或进行其他增产措施,如注二氧化碳开采、热力开采等。

图4 生产3个月后SRV单元内吸附气产出百分比分布Fig.4 Fraction distribution of adsorption gas produced in SRV after 3 months of production
3.2 气体运移机制的影响
在基本模型基础上,分别建立了考虑基岩不同运移模式的数学模型。模型一:基岩中运移机制仅为黏性流动;模型二:基岩中运移机制考虑黏性流动和Knudsen 扩散;模型三:基岩中运移机制考虑黏性流、Knudsen扩散以及多孔介质孔隙壁面吸附层厚度和吸附层表面扩散。
图5 给出了模拟时间为10 a 时基岩不同固有渗透率条件下运移机制对应的累计产气量曲线。可知:当k∞>10-5μm2时,由于孔隙尺寸较大,基岩中气体运移以黏性流为主导,分子与壁面碰撞产生的Knudsen 扩散和吸附层的表面扩散对压裂水平井产能影响不大,可以忽略;当10-7μm2<k∞<10-5μm2时,由于基岩孔隙尺寸的减小,分子与壁面碰撞产生的Knudsen扩散影响变大,对压裂水平井产能的影响变大,不可忽略,而吸附层表面扩散的影响可以忽略;当k∞<10-7μm2时,由于基岩孔隙尺寸很小,此时气体在基岩中的运移以Knudsen扩散为主,对压裂水平井的产能贡献最大,同时吸附层的表面扩散对压裂水平井产能的影响变大,不可忽略。平桥区块渗透率为5×10-8μm2,进行产能评价时必须要考虑黏性流、Knudsen 扩散、表面扩散等流动机理,否则会低估单井EUR。
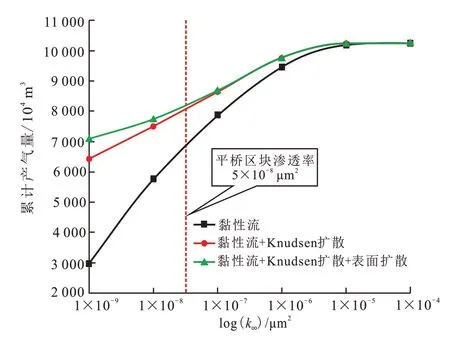
图5 不同运移机制下累计产气量曲线Fig.5 Cumulative production predicted by different transport model
图6 给出了焦页X—3HF 井实际产量和数值模拟产量拟合曲线。可以看出模拟产量与实际产量拟合较好,与平桥区块页岩气井的产量递减规律一致。压裂水平井的产量在初始1~2年内迅速下降,由7.5×104m3/d下降至2×104m3/d左右,后期产量趋于稳定,产量递减趋势变缓。
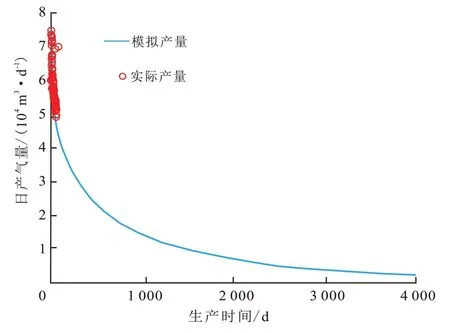
图6 数值模拟产量与实际产量拟合曲线Fig.6 Fitting curve between numerical simulation and actual production
3.3 天然裂缝连通性影响
当人工压裂没有穿透天然裂缝网络时,天然裂缝与人工裂缝沟通较差。在上述基本模型基础上降低天然裂缝密度,并去除与人工裂缝相连的天然裂缝进行研究。图7给出了裂缝网络连通性及应力敏感性对累计产量的影响。由图可知,当裂缝网络连通性很好的时候,生产100个月后累计产量可达8 305×104m3,连通性差的情况下累计产量仅有4 066×104m3,因此,只有当储层改造区域内人工裂缝沟通天然裂缝才能增加井的产量。同时还可以看出,裂缝网络连通性越好,考虑应力敏感性后对累计产气量影响越大。连通性好的情况下,考虑应力敏感后生产100个月累计产量减少304×104m3,而连通性差的情况下生产100个月后累计产量仅减少30.9×104m3。
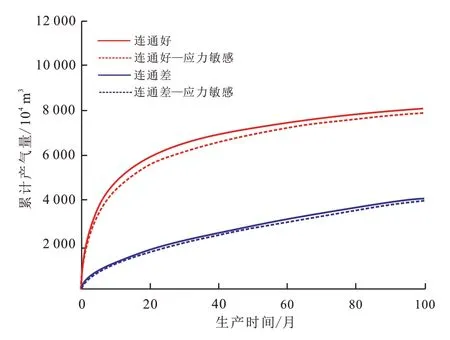
图7 不同裂缝连通性下累计产量变化曲线Fig.7 Cumulative production with different fracture connectivity
3.4 天然裂缝密度的影响
在上述基本模拟单元基础上,降低模型中天然裂缝的密度进行模拟。图8 给出了高密度裂缝模型和低密度裂缝模型累计产量和产量递减的趋势。可知,天然裂缝密度越大,累计产量越高,生产100个月时累计产气量为9 399×104m3,而低密度裂缝累计产气量仅为4 676×104m3。同时裂缝密度越大,产量递减率也越高,特别是生产前3 年,二者递减率差值最大可达10%。

图8 不同天然裂缝密度下累计产量和产量递减率变化曲线Fig.8 Cumulative production and production decline rate under different density of natural fractures
3.5 储层未改造区域渗透率的影响
在基础模型之上增加储层未改造区域,此时模拟区域大小为400 m×100 m×50 m,未改造区域仅存在基岩。图9 给出了不同基岩渗透率下考虑储层未改造区域时对累计产气量的影响。可知考虑储层未改造区域后,模拟区域原始地质储量增加,压裂水平井产量也增加,同时基岩渗透率对累计产气量的影响极大。当基岩渗透率较大时,生产不长时间就能看出储层未改造区域对累计产量的影响,累计产气量显著增加。相反,如果基岩渗透率很低时,储层未改造区域对累计产量的影响变弱,累计产气量增加不显著。从图中数据可以得出,当不存在未改造区域时,基岩渗透率从5×10-9μm2增加到25×10-9μm2和100×10-9μm2,生产10 a时的累计产气量分别增加了10.67%和20.67%;当存在未改造区域时,基岩渗透率从5×10-9μm2增加到25×10-9μm2和100×10-9μm2,生产10 a 时的累计产气量则分别增加了19.66%和48.69%。由于储层未改造区域的存在,使得基岩渗透率对累计产量的影响会放大。因此,在压裂施工时应对压裂设计方案和现场施工进行优化,尽可能的增大储层改造范围,降低未改造体积占比。
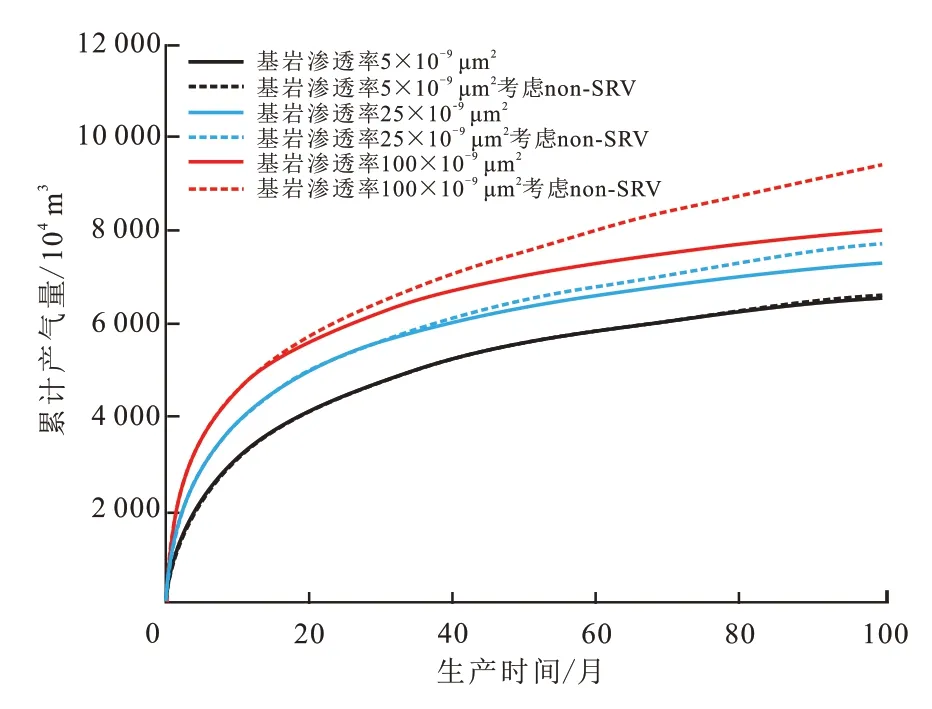
图9 不同基岩渗透率下考虑和不考虑non-SRV时累计产量变化曲线Fig.9 Cumulative production with and without non-SRV under different matrix permeability
4 结论
1)利用数值模拟预测平桥区块单井产量时,必须考虑黏性流、Knudsen扩散、表面扩散等流动机理,否则会低估单井EUR。
2)平桥区块页岩气水平井生产早期吸附气采出程度非常低,平均只有10.1%,早期产量主要来自裂缝系统游离气,吸附气主要在中后期做贡献。
3)天然裂缝密度和连通性对压裂水平井的产量影响很大。天然裂缝密度越高,连通性越好,压裂水平井的产量和累计产量显著增加,同时产量递减率也大大增加。考虑天然裂缝应力敏感效应后,随着压力降低,天然裂缝导流能力下降,压裂水平井产量下降,产量递减率也降低。
4)由于压裂改造不充分导致存在储层未改造区域,会极大的影响页岩气压裂水平井的产量,因此要对压裂设计及现场施工参数进行优化,尽可能增大储层改造范围,降低未改造体积占比。
