热致混合式转子变结构与动力学特性

潘健智，魏大盛，胡伟男

（1.南京理工大学 理学院，南京210094； 2.北京航空航天大学 能源与动力工程学院，北京100083）

大型旋转机械（如航空发动机、汽轮机等）多在高温和高压的环境中高速运转，并伴有负载较重，但其结构复杂且轻质化的发展趋势，使得对于运行时振动与抑制振动问题的研究越发成为发动机研发过程中的核心课题之一。根据现有的工作故障数据与相关实验验证对比结果显示，由机组主转子系统振动直接引发的故障占总故障的半数以上，是诱发机组异常振动的主要因素［1-2］。以航空发动机主转子结构为研究对象，文献［3-5］针对发动机整机振动问题展开了详细的研究，揭示了设计参数与转子振动特性的关系；Glasgow和Nelson［6］运用复模态综合法分析了航空发动机支承-转子-机匣整机系统的动力学特性；Hosseini和Khadem［7］研究了转子系统的自由振动，并考虑了转轴曲率和惯性；刘杨等［8-9］研究了故障转子振动的参数影响规律与抑制；文献［10］建立了具有复合材料轴-盘-轴承转子系统的数学模型，揭示了复合材料转轴对转子动力学特性的影响。针对航空发动机工况下的复杂结构变化和影响因素，以及诱发异常整机振动，文献［11］研究了考虑磨损引起的结构变化及产生的附加激励；文献［12-14］研究了复杂工况下热变形诱发的转子结构变化与运行时的故障振动的参数影响规律。

现有的研究工作多以集中质量方法予以建模及深入研究，对结构参数的影响或是复杂因素影响下结构变化引起的动态特性变化的研究较为少见。发动机作为飞行器的推进系统，其将燃料燃烧产生的化学能转变为有效的功率并以轴功率形式输出，最后传给推进系统。事实上发动机整机工作时，温度沿主轴方向呈现非均匀分布，涡轮要求的燃气温度随发动机推力需求的变化而变化，不同的性能需求对机组温升的要求也不尽相同。通常，最高温度限制在850～1 700℃，具体由涡轮转子叶片和导向器的材料决定；压缩过程所做的功已经将空气加热到200～550℃，使燃烧过程产生的温升达到650～1 150℃。鉴于以上研究现状与研究背景，本文考虑复杂温度环境引起的热膨胀及变结构特征，以Jeffcott转子动力学模型为基础，以文献［15］的单厚盘转子系统模型为主要研究对象，进一步考虑文献［16］中转轴热膨胀特性的理论研究结果，对比数值计算与理论研究，分析厚盘基于热膨胀沿轴向窜动后转子系统的动力学属性与参数影响规律。

1 盘鼓混合式转子系统建模

针对航空发动机等旋转机械的旋转构件结构特点和复杂连接形式，虽然涡轮与压气机处转盘厚薄不同，但两者的旋转构件均以复杂的形式连接［17］。本文以盘鼓混合式连接为例，即各级转盘间以鼓筒连接。

考虑图1中的盘鼓混合旋转构件的结构特点：实心圆截面转轴较为细长，与转轴相比，鼓筒为相对粗短的薄壁柱壳且空心圆截面轴惯性矩较大，因此整体旋转构件中鼓筒的弯曲刚度远远大于细长的转轴。将盘鼓混合连接结构刚化为理想刚性圆柱体，并视其为考虑厚度的转盘（简称厚盘）。考虑各转盘存在偏心距且质心连线与转轴平行，鼓筒为薄壁圆柱壳，忽略其质量影响。

图1 盘鼓混合旋转构件示意图Fig.1 Schematic diagram of mixing rotor set with turntable and drum

1.1 理想刚性圆柱体定义

如果圆柱体满足如下条件：

1）圆柱体的各向弯曲刚度、扭转刚度和剪切刚度无穷大，其各种形式的变形在理论研究中可忽略不计，即圆柱体为理想刚体。

2）圆柱体沿轴向质量分布绝对均匀，即圆柱体的每根轴向纤维为均匀的质量线。

3）圆柱体沿径向存在质量偏心量。

则称其为理想刚性圆柱体，如图2所示。

1.2 厚盘转子系统动力学模型

以理想刚性圆柱体为转盘，用以近似厚度不可忽略的盘鼓混合旋转构件，圆柱体两端分别与转轴刚性连接，且中心轴线和转轴中心线均与两支座连线共线；细长转轴为质量不计的实心圆截面弹性纯弯轴；忽略静置时重力引起的静变形量；转子两端支撑形式简化为光滑的固定铰支座和活动铰支座。基于理论研究，在微振幅范围内转盘偏转转角为微小角，即θ≈tanθ≈sinθ，且弧段长度近似等于弦段长，运行状态下转子上各点在z轴上投影在未发生热膨胀变形时近似不变。以l表示转轴总长度，d表示转轴截面直径。

如图3所示，在直角坐标系A-xyz下，初始静置状态下转子总跨度为AB＝L0，转盘厚度为2b，左右轴段AO1和O2B长度分别为l10和l20，转轴总长l0，则存在如下关系：

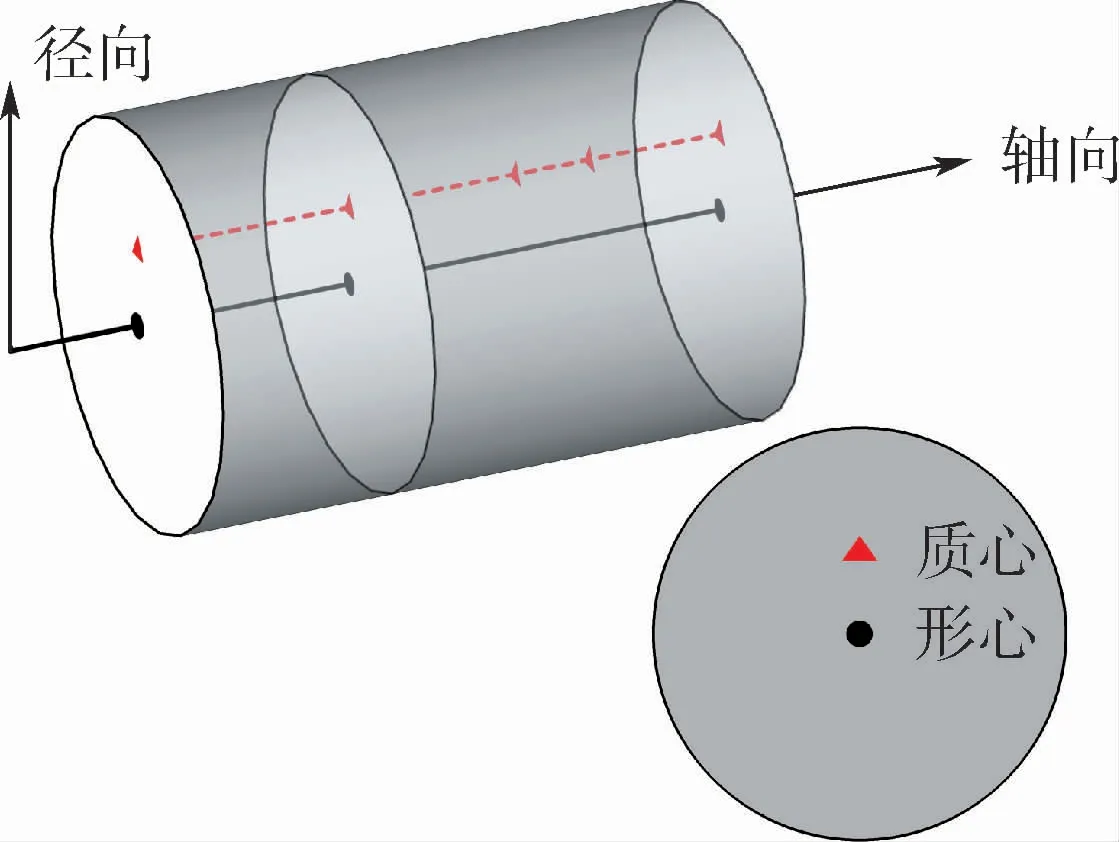
图2 理想刚性圆柱示意图Fig.2 Schematic diagram of ideal rigid cylinder

忽略厚盘热变形，转轴发生热致膨胀后左右段长度变为l1和l2，则转轴总长度与转子总跨度变为

转子以转速Ω运行时，厚盘的动量矩沿x、y方向的投影Lx和Ly为

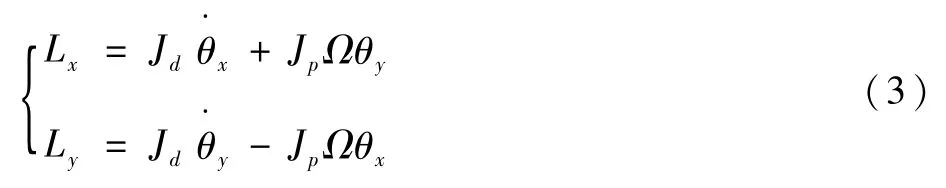
式中：θx、θy为转盘偏角；Jd和Jp分别为厚盘绕截面直径和中心轴转动惯量。

由动量矩定理，惯性力矩Mx和My为

图3 厚盘转子系统示意图Fig.3 Schematic diagram of rotor system with thick disk

厚盘的质量为m，且偏心量为ε，则厚盘惯性力在x和y方向的投影分别为m¨xr和m¨yr；系统受到等效黏性比例阻尼的比例系数为β1和β2。依转子在转盘处受力（力矩）和位移（转角）的关系及动力学普遍方程，可得厚盘转子系统的振动方程为

式中：转盘坐标X＝（xr yrθxθy）T；质量矩阵M＝diag（m，m，Jd，Jd）；刚度矩阵K＝陀 螺 力 矩H＝；比例阻尼C＝β1M＋β2K；F＝（mΩ2εcos（Ωt）mΩ2εsin（Ωt） 0 0）T为偏心激励。

如忽略厚盘的偏心量，且引入复变量r＝x＋iy，θ＝θy－iθx，则方程（5）变为

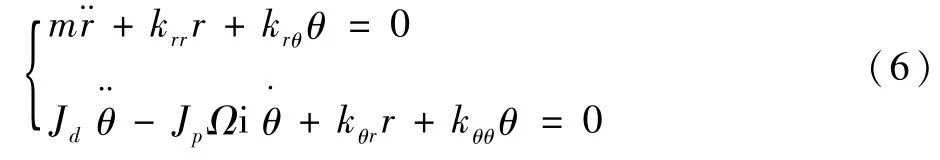
代回方程（6）可得频率方程为

依方程（8）求解出4个根，即转子系统存在4个进动频率［18-19］。

2 转轴弯曲刚度

转子系统运行温度的复杂多变及非均匀特性，使得高速运转中的主轴产生复杂多变的非均匀温度应力。考虑温度沿轴向的复杂分布规律，进而导致转盘产生轴向窜动。将转子材料的热膨胀系数近似为一常数α，即忽略温度对材料热膨胀属性的影响，并展开热膨胀对转子系统影响的研究。

2.1 热膨胀影响下转轴轴向窜动规律

当厚盘两侧轴段的温度由初始温度T0分别升至工作温度T1和T2时，厚盘转子模型的转轴发生热膨胀变形后，厚盘沿轴向窜动的示意图如图4所示。

热膨胀引起变形后各轴段长度为

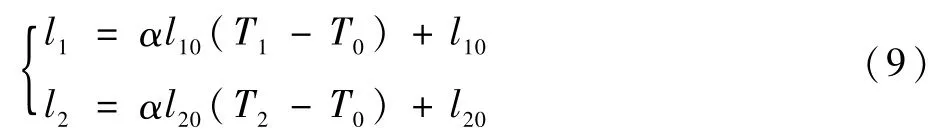
如图5所示，研究转轴截面变形，线弹性微小变形范围内，径向、轴向应变满足如下关系：

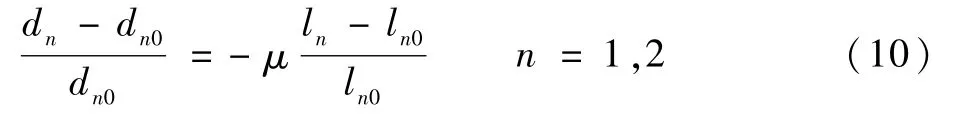
式中：μ为泊松比；截面直径d的角标意义与轴段l相一致。

将式（9）代入式（10）整理，可得变形后两轴段横截面直径为

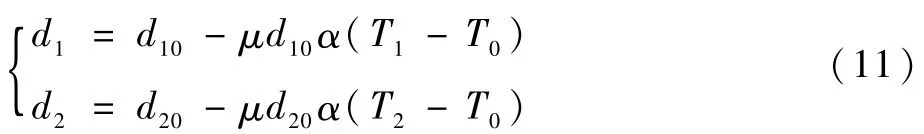
两轴段截面对其直径的轴惯性矩为

进一步，即可求得两轴段热膨胀后的抗弯曲刚度EI1和EI2（E为材料弹性模量）。

图4 转轴轴向窜动Fig.4 Axial movement of shaft

图5 转轴轴向窜动变形示意图（n＝1，2）Fig.5 Deformable diagram of axial movement of shaft（n＝1，2）

2.2 热膨胀影响下转轴弯曲刚度

图6为膨胀后的转子系统。基于厚盘变形可忽略且两端都与转轴刚性连接，如图7所示，当将，曲线AO1B为一条处处光滑且连续的曲线。

对曲线AO1B在坐标系Arz下进行数值拟合，转轴上任意一点处的径向位移r（z）为位置z的三次多项式：

式中：a1、a2、a3、a4为待定系数，可由如下插值条件确定，即多项式r（z）满足：

将插值条件式（14）代入多项式（13）得

由式（15）可将多项式（13）记为

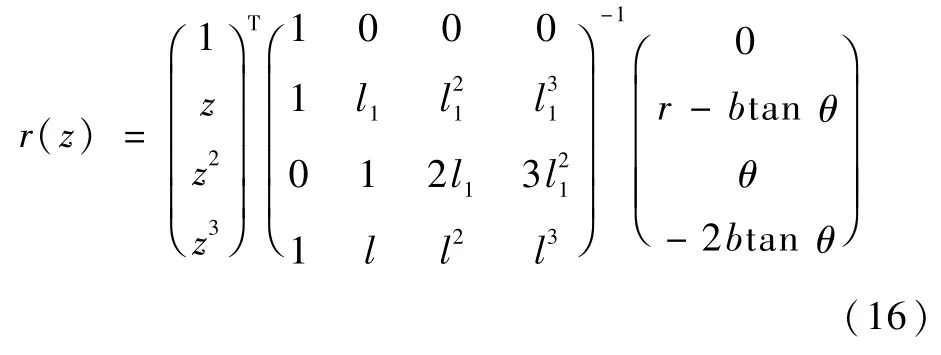
计算式（16）中矩阵的逆并记为I，选取关于变量z三次Hermite多项式［20］：

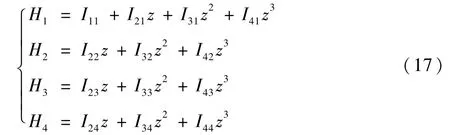
则式（16）的形式可记为

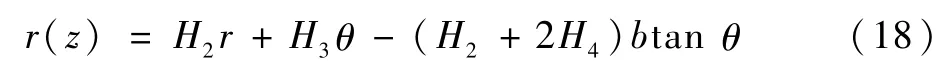
式中：z∈［0，l］。

当θ为微小角时，tanθ≈θ，则

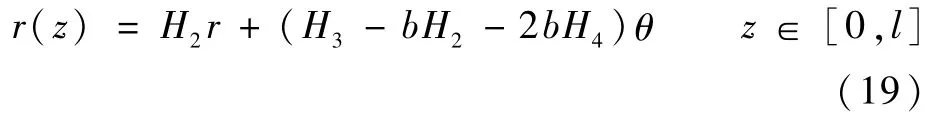
两段转轴的总弯曲势能与拟合曲线AO1B的曲率有关，与位置无关，厚盘转子系统转轴弯曲势能ur为

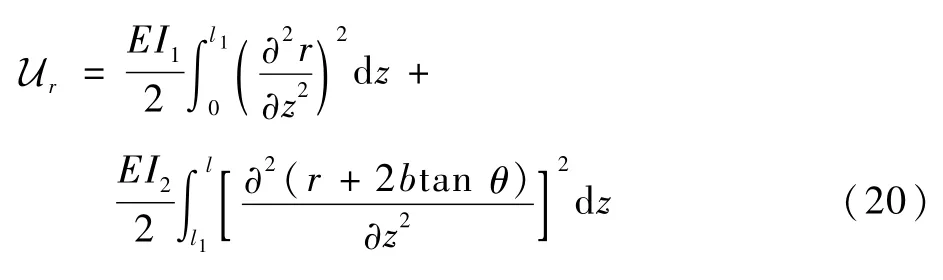
ur为一个关于r（z）的二次泛函，式（20）可退化为线性化表达式：

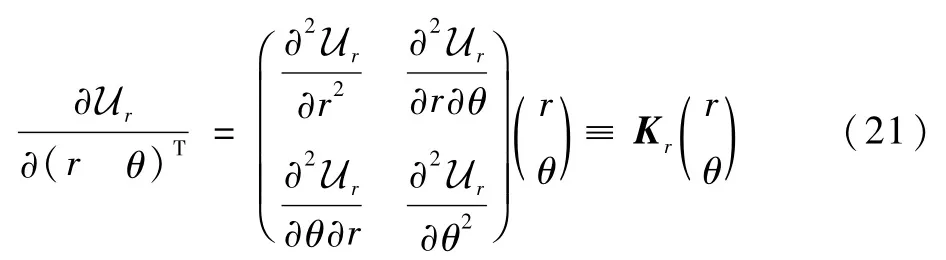
泛函ur也可以表示为

式中：K r为弹性转轴两端固定时弯曲恢复刚度矩阵，即

由于圆截面转轴截面各向同性，则转子在置盘处的弯曲恢复力（力矩）和位移（转角）的关系，即转子系统的弯曲刚度与恢复力满足：

图6 热膨胀转子弯曲示意图Fig.6 Bending diagram of rotor after thermal expansion

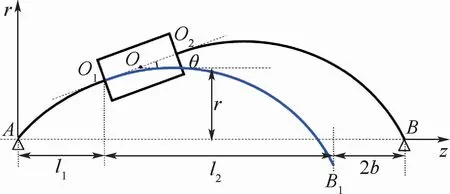
图7 弯曲转轴的曲线拟合Fig.7 Curve fitting of bending shaft

3 算例与分析

为研究热膨胀对厚盘转子系统动力学属性的影响，针对厚盘转子系统选取计算参数，如表1所示。

为模拟出复杂温度环境及温升过程对厚盘转子系统的影响，参考大型复杂旋转机械实际工况特点。当转子自然温度T0＝68 K时，分别以速率v1T＝0.8 K／s和v2T＝6 K／s匀速升温至稳定的工作温度T1W＝608 K和T2W＝2 192 K；热膨胀系数α＝4.8μm／mK。此时温升及轴段长度变化规律分别如图8和图9所示。

改革开放40年，黄淮白酒企业经历了各种波澜起伏，有过辉煌也有过挫折，有过迷茫也有过希望和成长，时至今日，苏、鲁、豫、皖四省白酒逐渐改变了过去说强不强、说弱不弱的“小而散”的状态。2017年四省规模以上企业近500家，白酒产量占据全国三分之一，白酒产量位列前五当中，河南、山东、江苏占据三席，因此，在如今这个重要的发展节点上，如何让黄淮名酒产区壮大，让黄淮名酒飘香世界，成为众多白酒企业思考的新命题。

表1 厚盘转子系统参数Table 1 Parameters of rotor system with thick disk

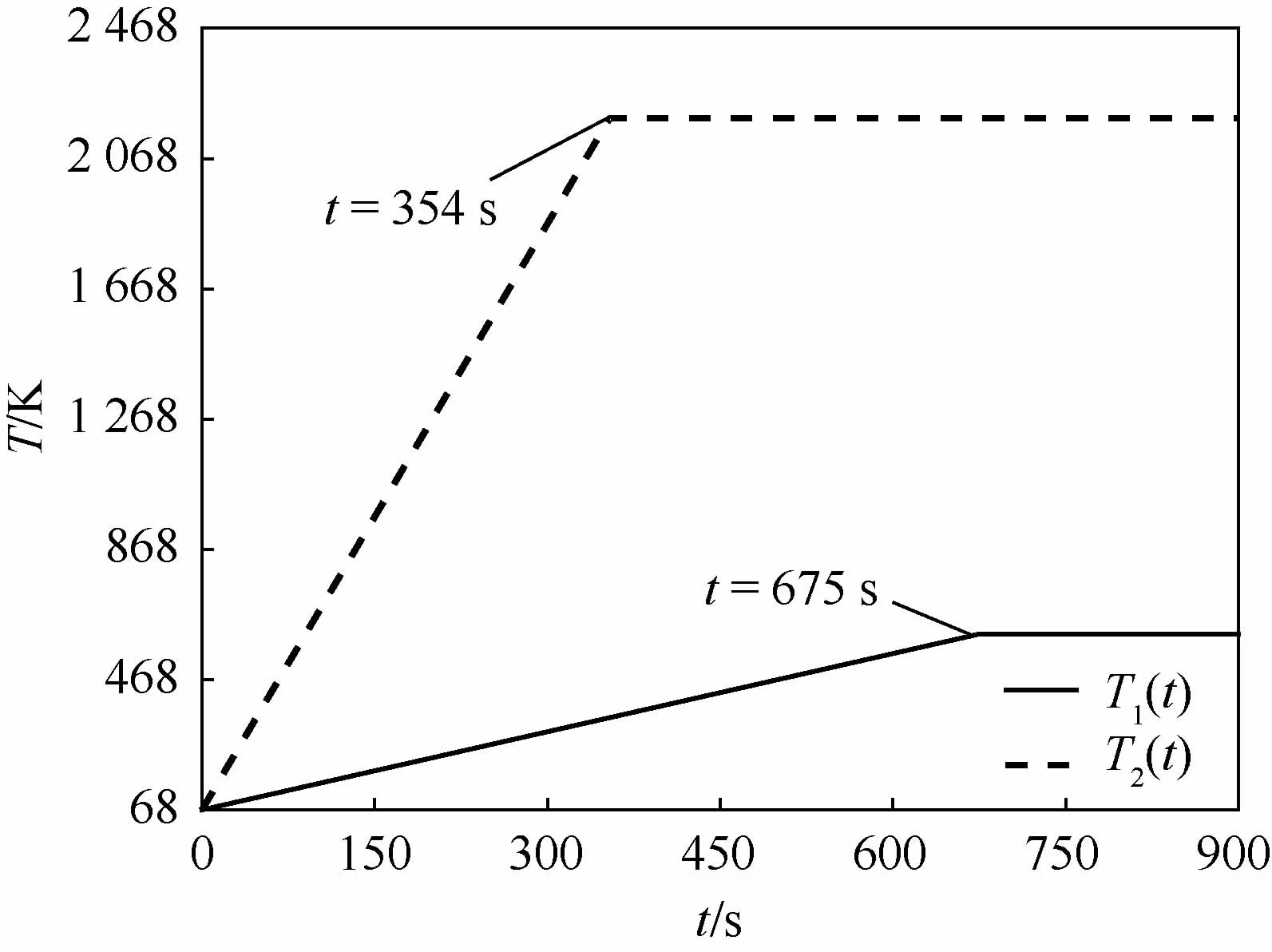
图8 温升曲线Fig.8 Temperature rising curves

图9 转轴长度变化Fig.9 Axial length variation

3.1 热膨胀影响下弯曲恢复刚度

转盘厚度2b＝0.2m时，计算对比厚盘转子系统在不同工作环境中的弯曲恢复刚度，列于表2和表3中。表2为工作温度T2W＝1652K时，T1W对转子主刚度的影响；表3为工作温度T1W＝608 K时，T2W对转子主刚度的影响。数据显示了在不同温度状态下对厚盘转子系统弯曲恢复刚度的影响。

表2数据显示，仅考虑T1W影响时，刚度krr、kθθ均随T1W增加而不同程度的减小，同时刚度krθ的绝对值也随之减小。表3数据显示，仅考虑T2W影响时，刚度krr和刚度krθ的绝对值随T2W增加而增加，而刚度kθθ随T2W增加而减小。

研究转盘厚度的影响时，令初始状态的自然温度为T0＝68 K；针对稳定的工作温度T1W＝608 K和T2W＝2 192 K，计算对比转子的弯曲恢复刚度列于表4中。由表4数据可见，当转轴长度不变时，转盘厚度对弯曲恢复刚度的参数影响规律为：刚度krr不受转盘厚度参数的影响，而刚度krθ、kθθ的绝对值均随转盘加厚而增加。

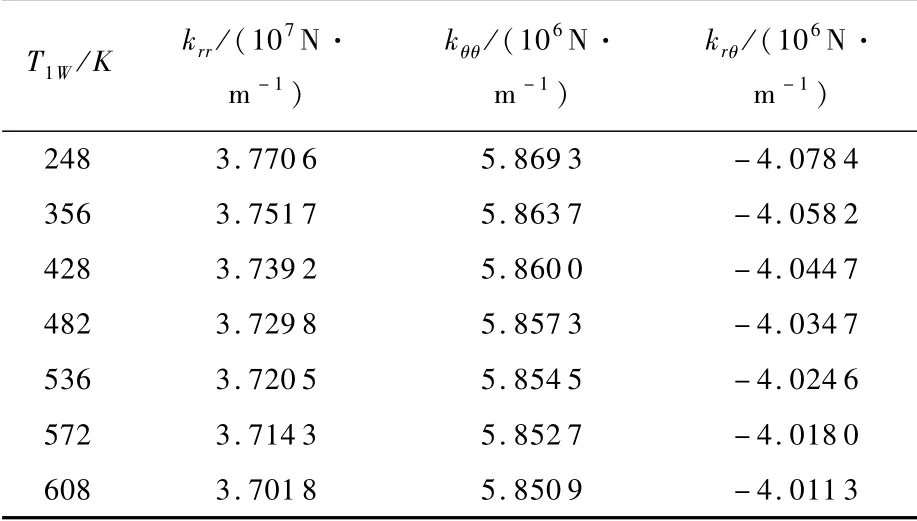
表2 弯曲恢复刚度受T1W的影响Table 2 Bending restoration stiffness affected by T1W

表3 弯曲恢复刚度受T2W的影响Table 3 Bending restoration stiffness affected by T2W

表4 弯曲恢复刚度受转盘厚度的影响Table 4 Bending restoration stiffness affected by disk thickness

3.2 热膨胀影响下转子进动频率

由方程（8）求解计算转子在不同转速Ω时的4个进动频率角速度，记ωf1和ωf2为正进动频率，ωb1和ωb2为反进动频率。绘制辅助线ωn＝Ω和ωn＝－Ω，由交点确定出厚盘转子系统在不同工况下的临界角速度。考虑稳定的工作温度T1W＝608 K和T2W＝2 192 K，热膨胀系数α＝4.8μm／mK。当b＝0.1m时求得转子进动频率，如图10（a）所示；当b＝0.2m时求得转子进动频率，如图10（b）所示。

表5为工作温度T2W＝1 652 K时，T1W对转子临界角速度进动频率的影响。表6为工作温度T1W＝608 K时，T2W对转子临界角速度的影响。

由图10可见，厚盘转子系统在发生一定程度轴向热膨胀后有3个临界角速度。而ωn＝Ω与ωf2无交点，也可认为ω4＝∞。2个正进动频率和2个负进动频率都随着转速Ω升高而升高。结合表5和表6数据，对于转盘厚度较大的厚盘转子系统，临界角速度ω1和临界角速度ω2较小，而临界角速度ω3则随着转盘厚度增加而增加。

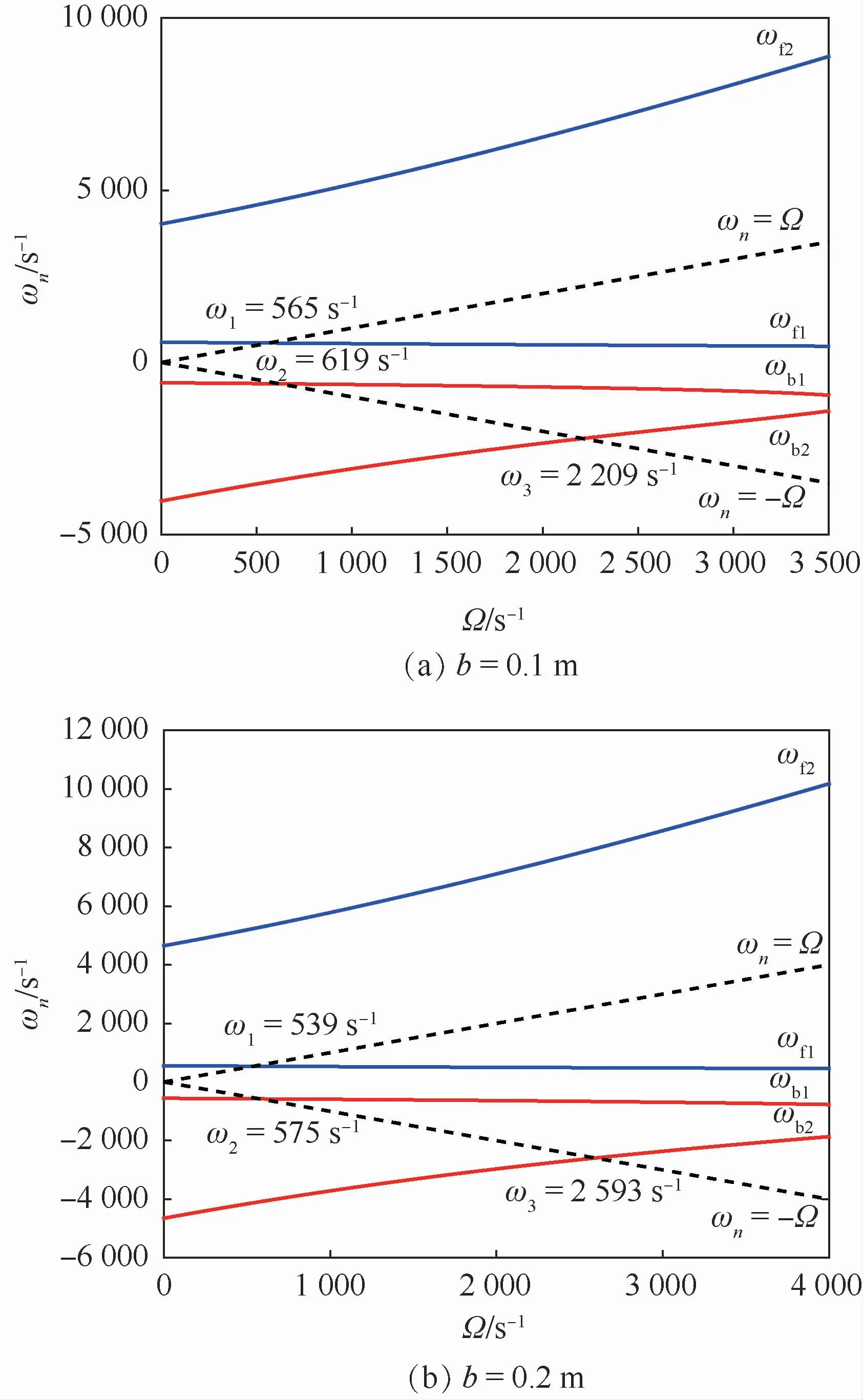
图10 转子进动频率Fig.10 Precession frequency of rotor

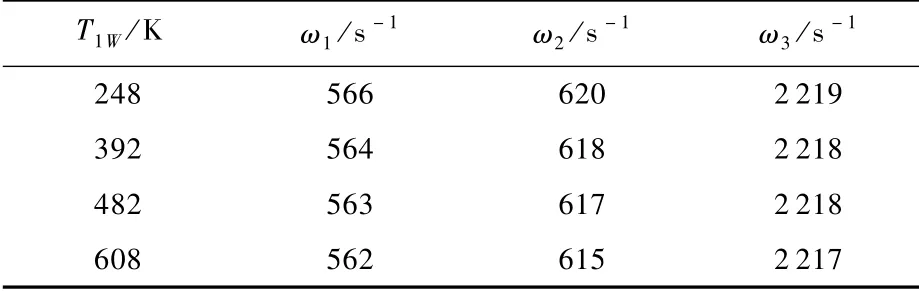
表5 临界角速度受T1W的影响Table 5 Cirtical angular velocity affected by T1W

特别当Ω＝0时，ωf1＝－ωb1＝ωα且ωf2＝－ωb2＝ωβ，即为不考虑陀螺力矩时的临界角速度。依温升规律（见图8）和转轴长度膨胀规律（见图9）对转子进行计算，对比仿真温升过程中ωα、ωβ的变化规律，如图11所示。

从图11中可以看出，在0～354 s时间段内，温度T1和T2均为升温状态下，ωα均随之增加而ωβ随之减小；在时间段354～675 s内，T2达到稳定的工作温度T2W而T1仍继续缓慢升温，在此时间段内ωα、ωβ均以不同速率减小；在675 s后温升结束，系统进入稳定的工作温度，ωα、ωβ保持不变。

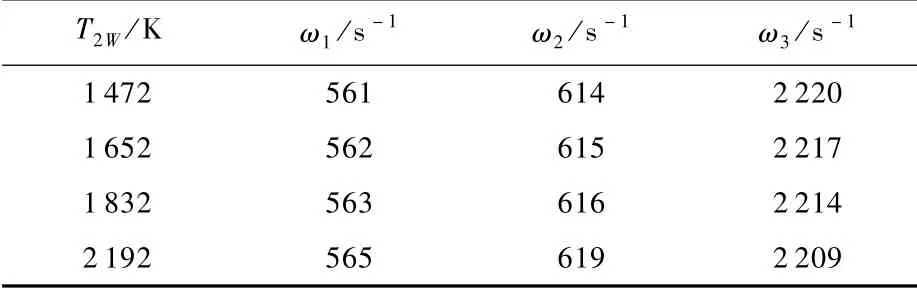
表6 临界角速度受T2W的影响Table 6 Cirtical angular velocity affected by T2W

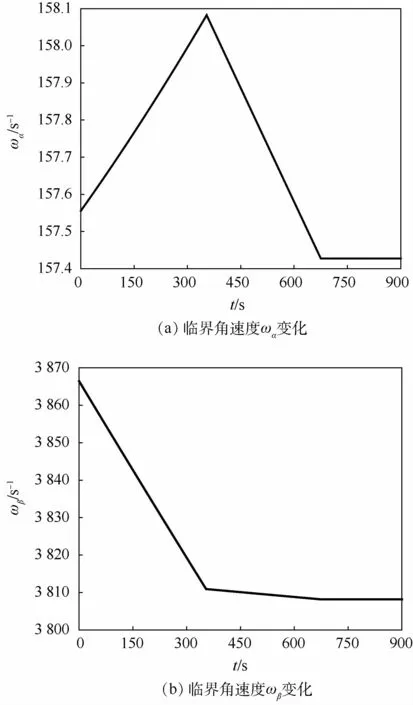
图11 临界角速度ωα、ωβ变化Fig.11 Changes of cirtical angular velocityωα andωβ

3.3 转轴截面直径对幅频特性的影响

如图12及表7所示，随着转轴截面直径d0增加，幅频特性曲线的峰值减小，且峰值对应的转速值变大。当转速小于383 s－1时，响应幅值随转轴直径在0.04～0.06m范围内增加而减小；当转速大于568 s－1时，响应幅值随转轴直径在0.04～0.06m范围内增加而增加。

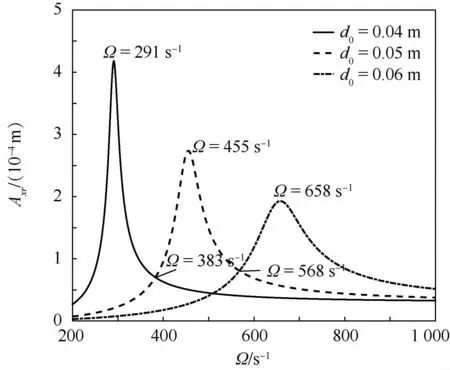
图12 转轴截面直径影响下响应xr的幅频曲线Fig.12 Amplitude-frequency curves of response xr under influence of shaft diameter

表7 图12中峰值及其对应转速Table 7 Peak value and corresponding rotation speed of Fig.12

3.4 工况温度对幅频特性的影响

为研究工况温度对厚盘转子系统的影响，以响应xr为例。首先考虑工况温度T2W＝1 652 K，转盘厚度2b＝0.2m，转轴截面直径d0＝0.05m，绘制不同工况温度T1W情况下厚盘转子系统响应幅值随转速的变化曲线，如图13所示（虚线和点划线的交点处Ω＝456.6 s－1，实线和虚线的交点处Ω＝459.8 s－1），相应峰值列于表8；其次考虑工况温度T1W＝932 K，转盘厚度2b＝0.2 m，转轴截面直径d0＝0.05m，绘制不同工况温度T2W情况下厚盘转子系统响应幅值随转速的变化曲线，如图14所示（虚线和点划线的交点处Ω＝457.0 s－1，实线和虚线的交点处Ω＝457.6 s－1），相应峰值列于表9。

如图13及表8所示，随着工况温度T1W增加，幅频特性曲线的峰值增加，且峰值对应的转速值减小。当转速小于456.6 s－1时，响应幅值随工况温度T1W增加而增加；当转速大于459.8 s－1时，响应幅值随工况温度T1W增加而减小。

图13 T1W影响下响应xr的幅频曲线Fig.13 Amplitude-frequency curves of response xr under influence of T1W

表8 图13中峰值及其对应转速Table 8 Peak value and correspond ing rotation speed of Fig.13

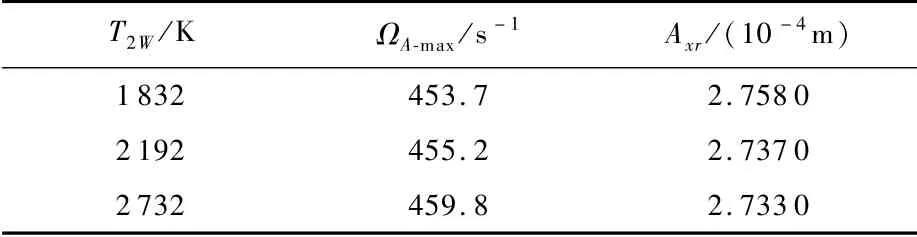
表9 图14中峰值及其对应转速Table 9 Peak value and correspond ing rotation speed of Fig.14

如图14及表9所示，随着工况温度T2W增加，幅频特性曲线的峰值减小，且峰值对应的转速值增加。当转速小于457.0 s－1时，响应幅值随工况温度T2W增加而减小；当转速大于457.6 s－1时，响应幅值随工况温度T2W增加而增加。

3.5 转盘厚度对幅频特性的影响

为研究转轴截面直径对厚盘转子系统的影响，以响应xr为例。考虑工况温度T1W＝932 K，T2W＝1 832 K；转轴截面直径d0＝0.05m。绘制选取不同转盘厚度情况下厚盘转子系统响应幅值随转速的变化曲线，如图15所示，相应峰值列于表10。

如图15及表10所示，随着转盘厚度的增加，幅频特性曲线的峰值减小，且峰值对应的转速值较小。当转速小于414 s－1时，响应幅值随转盘厚度的增加而增加；当转速大于438 s－1时，响应幅值随转盘厚度的增加而减小。

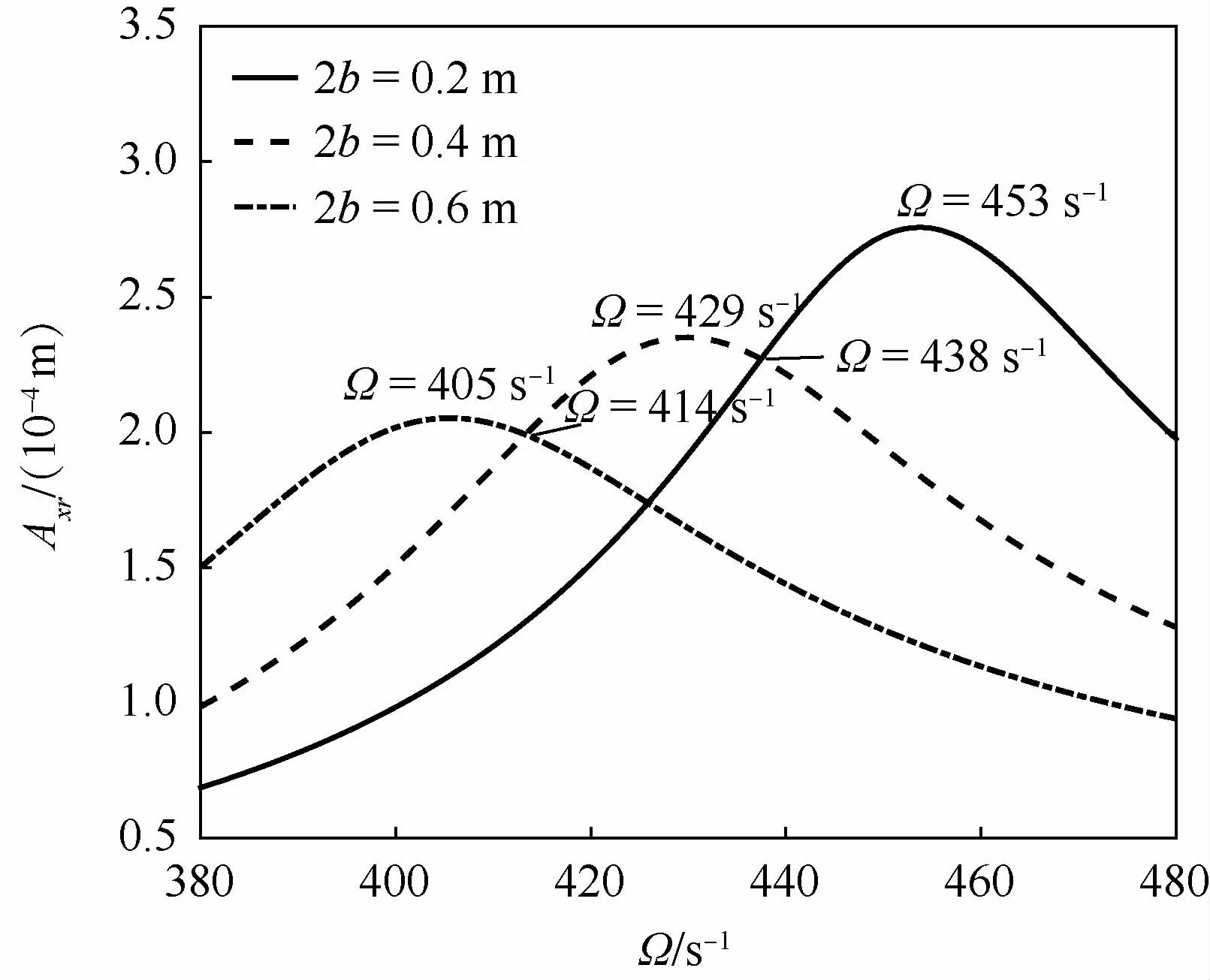
图15 转盘厚度影响下响应xr的幅频曲线Fig.15 Amplitude-frequency curves of response xr under influence of disk thickness

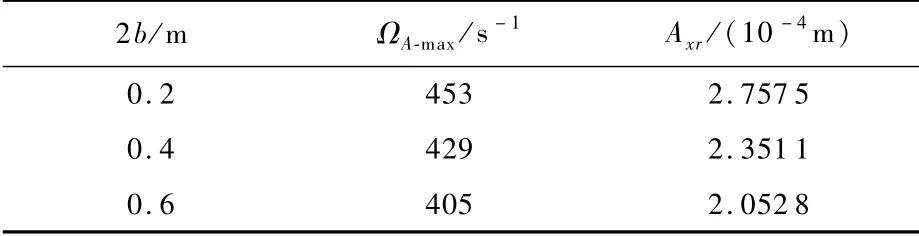
表10 图15中峰值及其对应转速Table 10 Peak value and corresponding rotation speed of Fig.15

4 结 论

复杂多变的温度环境会使转子系统结构变化，是影响转子动力学特性及旋转机械异常振动分析的主要因素之一。本文考虑了转盘厚度的影响，并开展了厚盘转子系统建模与热膨胀变形的研究，针对温升过程及高温运行环境，将其影响量化，研究了热膨胀量对厚盘转子系统结构与运行特性的影响。通过数值仿真及对比算例，展示了厚盘转子系统动力学特性受热膨胀因素的影响规律。

1）从转轴弯曲恢复刚度分析结果可见，在温升过程中，厚盘转子系统以热膨胀变形规律发生结构变化，其弯曲恢复刚度各项均随之以不同规律变化，因而热膨胀变形量引起的厚盘转子系统结构参数变化是影响弯曲恢复刚度估算的因素之一。

2）从转子进动频率和临界转速的分析结果可见，当转轴长度不变而转盘厚度变化，转子系统的各阶临界角速度均受影响；当考虑工作温度环境时，在一定的升温工作状态和稳定的高温工作状态，热膨胀变形是影响转子临界转速的主要因素之一。

3）对于产生轴向窜动的厚盘转子系统，不同的工况所产生的热膨胀窜动量有所不同，使得相同的厚盘转子系统在不同的工况下以不同的结构参数运转，特别在不同的转轴结构参数下具有不同的弯曲恢复刚度，使得系统的固有频率和幅频特性等动力学特性均受到影响。

4）厚盘转子系统的转盘厚度也是影响整个转系统动力学特性的主要因素，即便工况状态下厚盘转子系统的转轴结构参数相同，不同的转盘厚度使得整系统具有不同的结构特征，使得转子的弯曲恢复刚度具有差异而间接的影响整个厚盘转子系统的动力学特性。