基于一种启发式迭代算法的产品组合优化

张道恒 李敬泉

[摘    要] 本文研究了一个单个时期的产品组合优化问题。文章假定商品的需求符合MNL model。 笔者通过设计一种迭代算法从零售商所有能够经营的产品种类集合中挑选出在零售商库存约束范围内单位期望收益最大的產品集合作为其最优产品组合。数据实验表明该算法可有效提高零售商的期望收益，并为如何改进零售商经营的产品组合提供科学指导。

[关键词] 产品组合优化; 启发式迭代算法;MNL model

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2020. 01. 044

[中图分类号] F273    [文献标识码]  A      [文章编号]  1673 - 0194（2020）01- 0104- 03

对于零售商存在库存约束时的产品组合选择问题，大部分现有研究都是在使用MNL模型等消费者选择模型（Nested Logit Model，Mixture of  MNL Model，etc）表示产品需求的基础上，进而构建数学算法求解出能够使零售商期望收益最大化的产品集合以作为其最优产品组合。Désir，Goyal and Zhang（2016）分别研究了消费者选择服从MNL、MMNL以及NML模型的具有库存容量约束的产品组合优化问题。他们设计了一种与解决背包问题的算法类似的多项式时间近似算法用以从零售商可经营的产品集合中挑选出最优的产品组合。然而，当MMNL和NML模型中参数较多时，最优产品组合选择问题将会产生极大的求解难度甚至无法求解（Davis， Gallego and Topaloglu，2014）。

我们首先通过比较零售商所能经营的所有产品集合的单位期望收益（总期望收益除以顾客数）选择出期望收益最大的产品集合作为零售商经营的产品组合，I* 表示该最优产品集合。那么对应的组合（I*，Xi*）表示零售商的最优产品组合。在正式讨论最优产品组合之前，我们提出两个假设来限定零售商所能经营的产品种类的范围。

假设（1）：由于经营技术（产品知识、维修技术和保存技术等等）的制约，零售商经营有限种类的产品。

假设（2）：零售商只经营商业集聚中现有的产品种类。

基于上述假设，我们将设计一套算法解决最优产品集合的选择问题。此处，产品需求仍然由MNL模型表示;并且零售商可经营的产品种类最多为K（库存约束）。我们的目的是找出单位期望收益最大的且最多由K个产品组成的产品集合。

首先，我们构建一个函数来度量零售商所能经营的各产品组合的单位期望收益：

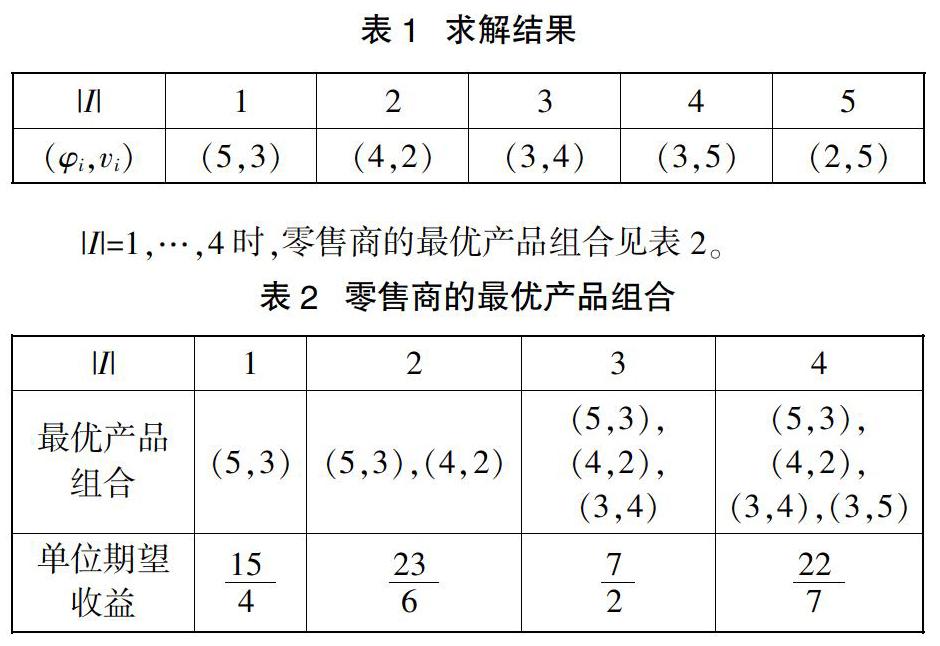
由表2可知零售商的最优产品集合为（5，3），（4，2），即零售商经营这两种产品时获得的期望收益最大。下面，我们以定理的形式简要地总结一下最优产品组合的结构。

定理（最优产品组合的结构）：零售商应当经营使得产品组合期望收益函数（2）取值最大的种产品（c≤k）。并且这c类产品可由上述的迭代算法（7）和（8）依次求出。

本文研究了一个消费者选择过程服从MNL模型的单个库存周期的产品组合优化问题。我们首先从零售商所有可以经营的产品种类中选择出最优的产品组合。我们的目标是找到零售商库存约束范围内单位期望收益最大的产品集合，并将其作为零售商的产品组合。为此，我们对产品组合的单位期望收益函数进行了敏感性分析，并在基础上设计了一个多项式时间迭代算法用以求解最优产品集合问题。最终，我们得出零售商应当经营其库存约束许可范围内尽可能多的产品，并运用迭代算法依次求出零售商应当经营的产品。零售商依据预期的商品需求量进行备货决策普遍存在于当今的零售业中。因此，我们有必要设计一种有效的需求预测方法以作为零售商的备货决策依据。而在较长的经营期限内，通过及时地更新产品组合中的商品品目使得畅销的商品进入产品组合中可显著提升零售商货品的销售率，进而增强其竞争力。

主要参考文献

[1]A Kǒk， L Fisher.Demand Estimation and Assortment Optimization under Substitution： Methodology and Application [J]. Operations Research，2007，55（6）：1001-1021.

[2]D Bertsimas，A Thiele.A Robust Optimization Approach to Inventory Theory [J]. Operations Research，2006，54（1）：150-168.

[3]P Rusmevichientong， Max Shen，D B Shmoys.Dynamic Assortment Optimization with a Multinomial Logit Choice Model and Capacity Constraint [J].Operations Research，2010，58（6）： 1666-1680.

[4]Z Li.A Single-Period Assortment Optimization Model [J].Production and Operations Management，2010，16（3）：369-380.

[5]P Rosmevichientong，D B Shmoys， C Tong，et al.Assortment Optimization under the Multinomial Logit Model with Random Choice Parameters [J].Production and Operations Management，2015，23（11）：2023-2039.