输电线路导地线和金具极限状态设计参数研究
2020-02-10张研,杨蕾,张军
张 研,杨 蕾,张 军
(1.河海大学力学与材料学院,江苏 南京 211100; 2.中国电力科学研究院输变电工程研究所,江苏 南京 210000)
架空输电线路是电力系统的重要组成部分,其运行状态的好坏将会对整个系统运行的可靠性产生较大影响[1]。随着中国经济的快速发展,对电力的需求更是呈直线增长,高压架空输电线路在实现电力的远距离、大容量输送方面发挥了重要作用。近年来,架空输电线路向着大截面、多分裂的方向发展,事故更趋频繁,严重威胁电网的安全稳定运行[2]。作为架空输电线路的重要元件,导地线和金具的可靠性更是直接影响了整个输电系统的安全和稳定。
结构可靠度理论采用概率论的方法描述结构的安全性,综合考虑了几何尺寸、所受荷载、材料性能、计算方法等不确定性因素,不同结构的安全性可以用可靠指标β统一衡量[3]。以可靠度理论为核心的分项系数法,即将容许应力设计表达式中的安全系数通过分离函数分解成荷载分项系数和抗力分项系数[4-6],比较好的解决了容许应力设计法存在的安全系数根据经验粗略取值、结构设计相当粗糙等问题,使结构设计更为科学合理。在国际上,随着结构可靠度理论的不断完善,可靠度设计法在输电线路中的应用越来越广泛,一些电力系统的相关规程正在逐渐淘汰容许应力设计法。
在1994年以前,我国输电线路的设计方法采用的是安全系数法,又被称为容许应力设计法[7]。用单一的安全系数来表示结构的安全度,没有考虑到作用于结构上的荷载和结构抗力的随机性,不具备科学性和严谨性,无法准确反映结构的安全性。在1994年之后,考虑到线条风荷载的影响,在输电线路设计表达式中加入了调整系数;1999年随着DL/T 5092—1999《110~500 kV架空送电线路设计技术规程》[8]的颁布,我国开始采用以概率论为基础的可靠度设计法和分项系数设计表达式。
在我国当前的输电线路设计规范中,杆塔和地基基础采用可靠度设计法,而导地线和金具依然采用传统的安全系数设计法进行设计,其中又分考虑和不考虑线条风荷载调整系数[9]2种情况,这使得我国输电线路在设计过程中需要采用2种不同的方法,可靠度水平没有一个明确的指标,加大了输电线路体系可靠度确定的难度。为了保持设计的统一性,同时与国际接轨,输电线路导地线和金具也采用可靠度设计法进行设计。
可靠度设计主要是通过数据分析, 得到导地线和金具的抗力与荷载统计参数; 然后, 基于当量正态化法(JC法)对按现行国家标准GB 50545—2010[10]和行业标准DL/T 5154—2012[11]设计的导地线和金具进行可靠度校准, 得到对应的可靠指标, 选取目标可靠指标计算得到导地线和金具的荷载和抗力分项系数,为实际输电线路工程的设计和可靠度理论在输电线路领域的推广提供了参考。
1 可靠度校准
极限状态是用来描述结构是否能符合结构设计中规定的某一个功能需求的状态,是用来区分构件的运行状态是否可靠的分界线,当超过极限状态时,就认为结构原来的特性发生了改变。可靠度校准的对象主要是按当前正在实行的规范GB 50545—2010和DL/T 5154—2012设计的输电线路的导地线和金具。
1.1 荷载统计参数
一般用均值系数k和离散系数δ来表示结构的荷载统计参数,k为均值与标准值的比值,δ为均方差与均值的比值。根据概率特性的不同,将输电线路可靠度设计过程中涉及的荷载按照其随时间变化的特性分成恒荷载和活荷载(活荷载一般考虑风荷载和覆冰荷载)。
1.1.1 恒荷载
恒荷载是指不随时间变化或者随时间变化的值与其均值比起来可以忽略不计的荷载。输电线路中的恒荷载主要指的是元件的自重。根据建筑结构规范的统计资料,恒荷载服从正态分布,均值系数取k=1.06,离散系数取δ=0.07。
1.1.2 风荷载
风荷载在输电线路中的设计沿用了建筑结构规范中的相关模式,服从极值Ⅰ型分布[12],在设计过程中考虑2种组合情况。当考虑输电线路只承受自重和风荷载时,参考建筑结构设计规范,取风荷载的均值系数kWT=0.999,离散系数δWT=0.193[13]。当考虑承受自重、风荷载和覆冰荷载时,由于覆冰存在时风速不会太大,可适当降低代表风速[14],取10 m/s。假设该风速为在1年中覆冰最严重的一个月的最大情况,风荷载均值的计算公式为
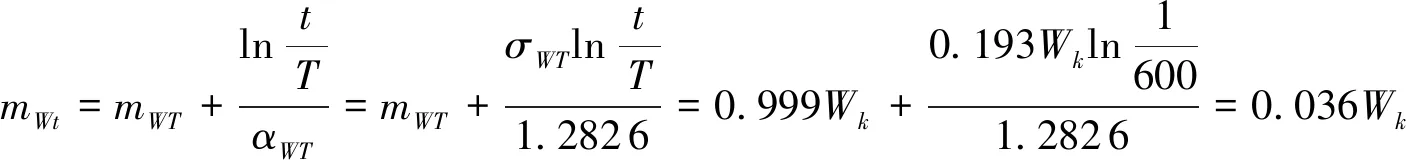
(1)
式中:mWt——结构承受风荷载与覆冰荷载时风荷载的均值;mWT——风荷载为结构承受的唯一活荷载时风荷载的均值;t——1年中覆冰最严重的时期;T——风荷载的重现期(50 a);αWT——符合极值Ⅰ型分布的尺度参数;σWT——风荷载为结构承受的唯一活荷载时风荷载的均方差;Wk——荷载规范[15]规定的风荷载标准值。
由式(1)可得风荷载的均值系数kWT=0.036,仍假定风荷载的离散系数δWT=0.193。
1.1.3 覆冰荷载
当前能够直接观测到的自然覆冰的情况和相关气象资料不多时,想要统计分析相关的分布、进行定量计算相当困难。本文参考冯云芬[7]的论文关于湖北恩施某输电线路观测站的导线25 a的年最大覆冰实测结果数据,进行了统计分析,并结合工程经验判断,覆冰荷载服从极值Ⅰ型分布,均值系数取1.1,离散系数取0.3。

表1 导地线拉断力统计参数
注:kTp,j、σTp,j、δTp,j分别为拉断力的均值系数、标准差和离散系数。
1.2 抗力统计参数
输电线路元件的抗力是构件抵抗各项荷载的能力,通过其整体的破坏荷载统计参数和计算模式不确定性来体现,不需要涉及几何尺寸、材料性能等其他参数。
1.2.1 导地线的抗力
根据收集到的4种类型导地线的拉断力计算得到的导地线统计参数如表1所示。
经过计算[7]得到导地线拉断力的统计参数kTp=1.038,σTp=0.093,δTp=0.09。导地线的抗力可表示为
R=Ωp1Tp
(2)
式中:Ωp1——导地线抗力计算模式不确定性系数,用以描述导地线在实际受力和试验受力状态下的区别;Tp——导地线的拉断力。
导地线抗力的均值系数和离散系数为
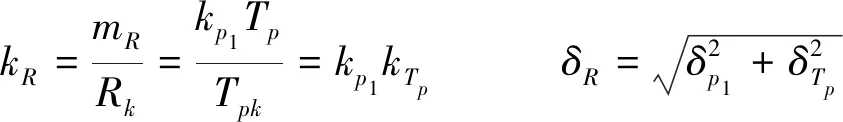
(3)
式中:mR——导地线抗力的均值;Rk——导地线抗力的标准值;Tpk——导地线拉断力的标准值;kp1、δp1——导地线抗力计算模式不确定性系数的均值系数和离散系数,分别取1.05和0.07。
由式(3)得到导地线抗力的统计参数kR=1.09、δR=0.114,认为导地线的抗力服从对数正态分布。
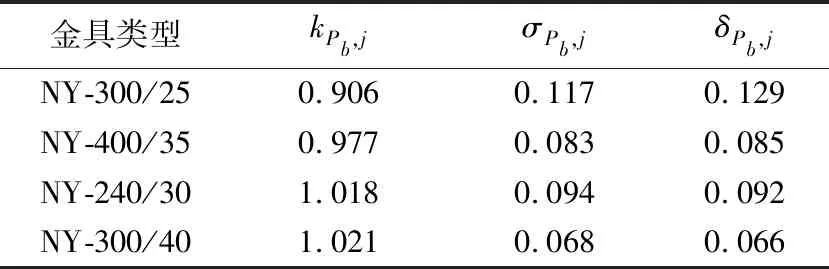
表2 金具破坏荷载统计参数
注:kPb,j、σPb,j和δPb,j分别为破坏荷载的均值系数、标准差
和离散系数。
1.2.2 金具的抗力
金具是指在电力系统中用于将电线与电线,以及电线与设备或材料进行固定、连接、接续、保护的已经定型化的金属部件。根据收集到的4种类型金具的破坏荷载计算得到的金具统计参数如表2所示。
计算得到金具破坏荷载的统计参数kPb=0.981,σPb=0.091,δPb=0.092。金具的抗力可表示
R′=ΩP2Pb
(4)
式中:ΩP2——金具抗力计算模式不确定性系数,反映金具在实际受力和试验受力状态下的区别;Pb——金具的破坏荷载。
金具抗力的均值系数和离散系数为
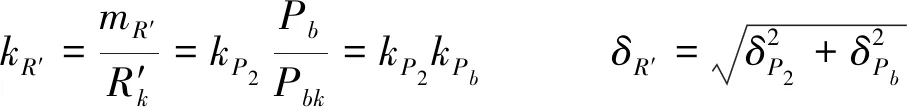
(5)

由式(5)得到金具抗力的统计参数为kR′=1.03、δR′=0.116,考虑金具的抗力服从对数正态分布。
1.3 荷载和抗力统计参数汇总
恒荷载服从正态分布,均值系数取1.06,离散系数取0.07;风荷载服从极值Ⅰ型分布,活荷载仅为风荷载时均值系数取0.999、离散系数取0.193,活荷载为风荷载和覆冰荷载时均值系数取0.036、离散系数取0.193;覆冰荷载服从极值Ⅰ型分布,均值系数取1.1,离散系数取0.3。导地线和金具的抗力都服从对数正态分布,均值系数分别取1.09和1.03,离散系数分别取0.114和0.116。
1.4 可靠指标计算
1.4.1 导地线可靠指标计算
参考GB50545—2010中关于导地线设计的规定,导地线的最大张力为
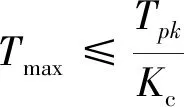
(6)
式中:Tmax——导地线在弧垂最低点的最大张力设计值;Kc——导地线的设计安全系数,风荷载和恒荷载作用时,弧垂最低点和悬挂点分别不小于2.5和2.25(风荷载、恒荷载和覆冰荷载共同作用时,弧垂最低点和悬挂点分别不小于1.4和1.3)。
按照GB50545—2010的规定,得到最小失效荷载的标准值为
Rk=Tpk=KcTmax=Kc(TGk+∑TQik)
(7)
式中: TGk——导地线恒荷载产生的拉力标准值;TQik——第i个可变荷载作用于导地线产生的拉力标准值。
导地线的受力的功能函数方程为
Z=R-TG-∑TQi
(8)
式中: TG——导地线恒荷载产生的拉力;TQi——第i个可变荷载作用于导地线产生的拉力。
导地线恒荷载产生的拉力的均值和均方差可表示为
mTG=kTGTGkσTG=δTGmTG=δTGkTGTGk
(9)
式中:δTG、kTG——导地线恒荷载产生的拉力的离散系数和均值系数。
第i个可变荷载作用于导地线产生的拉力的均值和均方差为
mTQi=kTQiTQikσTQi=δTQimTQi=δTQikTQiTQik
(10)
式中:δTQi、kTQi——第i个可变荷载作用于导地线产生的拉力的离散系数和均值系数。
考虑2种荷载组合的情况:
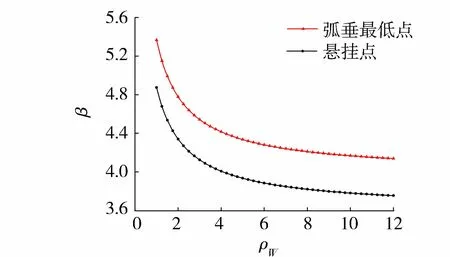
图1 导地线抗力可靠指标(恒荷载+风荷载)Fig.1 Reliability index of grounding wire resistance under dead load and wind load
a. 恒荷载与风荷载组合。当恒荷载与风荷载组合时,由式(9)可得到恒荷载的均值和均方差,由式(10)可得到风荷载作用于导地线产生的拉力的均值和均方差。导地线抗力的均值为
mR=kRRk=kRKc(TGk+TWk)=kRKcTGk(1+ρW)
(11)
式中:TWk——风荷载作用于导地线产生的拉力标准值;ρW——风荷载效应与恒荷载效应之比。
取ρW=TWk/TGk=1.0~12.0,导地线抗力的可靠指标可用JC法计算得到,如图1所示。由图可知,导地线抗力可靠指标β与ρW成反比,弧垂最低点的可靠指标高于悬挂点。导地线弧垂最低点的平均可靠指标为4.372,悬挂点的平均可靠指标为3.968。
b. 恒荷载、风荷载和覆冰荷载组合。当恒荷载、风荷载和覆冰荷载组合时,根据式(9)计算恒荷载的均值与均方差,由式(10)可分别计算风荷载和覆冰荷载作用于导地线产生的拉力的均值和均方差。导地线抗力的均值为
mR=kRRk=kRKc(TGk+TWIk+TIk)=kRKcTGk(1+ρWI+ρI)
(12)
式中:TWIk——荷载组合下风荷载产生的导地线拉力的标准值;TIk——荷载组合下覆冰荷载产生的导地线拉力的标准值;ρWI——导地线覆冰时风荷载与恒荷载的比值;ρI——导地线覆冰时覆冰荷载与恒荷载的比值。
取ρWI=TWIk/TGk=1.0~3.0、ρI=TIk/TGk=1.0~4.0,采用JC法计算得到导地线抗力可靠指标,如图2所示。由图2可知,导地线抗力可靠指标与ρWI成正比,与ρI成反比。导地线弧垂最低点的平均可靠指标为3.157,悬挂点的平均可靠指标为2.898。
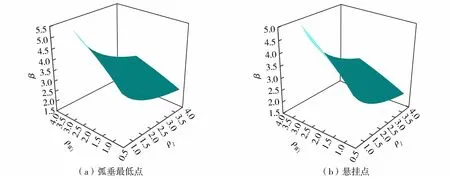
图2 导地线抗力可靠指标(恒荷载+风荷载+覆冰荷载)Fig.2 Reliability index of grounding wire resistance under dead load, wind load and ice load
1.4.2 金具可靠指标计算
金具的恒荷载为导地线的竖向荷载对金具产生的拉力,所受活荷载为导地线的横向荷载(风荷载)对金具产生的拉力。考虑导地线的活荷载只有风荷载的情况,金具的恒荷载均值系数取kW3=1.06,离散系数取δW3=0.07,活荷载均值系数取kW5=0.999,离散系数取δW5=0.193。
参考GB 50545—2010中的相关规定,金具承载力验算表达式为
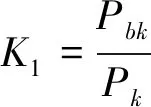
(13)
式中:K1——金具机械强度安全系数,运行状态下取2.5[16];Pk——金具正常运行时的荷载标准值。
若金具刚好满足设计要求,则
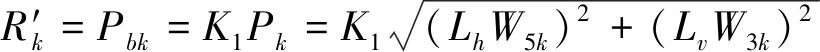
(14)
式中:Lh、Lv——水平档距和垂直档距;W5k——导地线的风荷载标准值;W3k——导地线的竖向荷载标准值。
金具的功能函数为
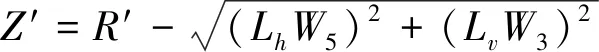
(15)
式中:W5——导地线的风荷载;W3——导地线的竖向荷载。
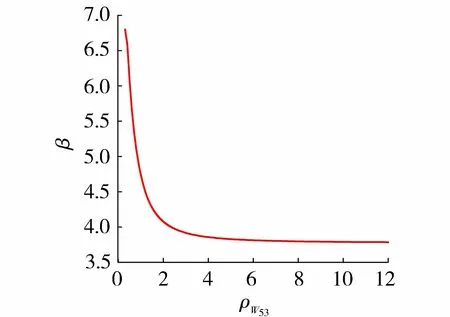
图3 金具的可靠指标(恒荷载+风荷载)Fig.3 Reliability index of fittings under dead load and wind load
金具受到的导地线竖向荷载和风荷载产生的拉力的均值和均方差分别为
mW3=kW3LvW3kσW3=δW3mW3=δW3kW3LvW3k
(16)
mW5=kW5LhW5k=kW3ρW53LvW3kσW5=δW5mW5=δW5kW3ρW53LvW3k
(17)
式中:ρW53——导地线风荷载与竖向荷载标准值的比值。
金具抗力的均值为
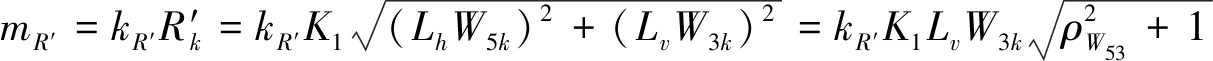
(18)
根据实际输电线路中导地线的受力监测统计结果,取ρW53=LhW5k/(LvW3k)=0.1~12。采用JC法计算得到金具的可靠指标并绘制成图(图3)。由图3可知,可靠指标β随着ρW53的增大而减小。金具的平均可靠指标为3.99。
1.5 可靠度校准结果汇总
不同荷载效应比时,对导地线和金具分别进行可靠度校准,得到了平均可靠指标。当恒荷载与风荷载组合时,导地线弧垂最低点和悬挂点的平均可靠指标分别为4.372和3.968;当恒荷载、风荷载和覆冰荷载组合时,导地线弧垂最低点和悬挂点的平均可靠指标分别为3.157和 2.898。考虑导地线的活荷载仅为风荷载的情况,金具的平均可靠指标为3.99。
2 设计参数研究
2.1 目标可靠指标
目标可靠指标是指考虑构件的材料特性和形状、受力特征等众多因素后选出的作为设计依据的可靠指标。根据建筑规范中的相关规定[17]:延性破坏安全等级为一级、二级和三级时,对应的目标可靠指标分别为3.7、3.2和2.7;脆性破坏安全等级为一级、二级和三级时,分别取目标可靠指标为4.2、3.7和3.2。对于工程结构来说,可以认为年失效率小于10-4是较安全的,小于10-5是安全的,而小于10-6则是很安全的。一般结构的设计基准期是50 a,因此当在结构的设计基准期内失效概率分别小于5×10-3、5×10-4、5×10-5时,可以认为结构较安全、安全和很安全。可靠指标β与失效概率Ρf的对应关系[18]如下:β为1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5时,对应的Ρf分别为1.59×10-1、6.68×10-2、2.28×10-2、6.21×10-3、1.35×10-3、2.33×10-4、3.17×10-5、3.40×10-6。由此可知,结构安全相应的可靠指标约在2.5~4.0之间。
由可靠度校准结果可知,当仅受恒荷载和风荷载作用时,按当前输电线路设计规范设计的导地线和金具的可靠指标远高于安全等级为一级的属延性破坏的结构构件的目标可靠指标3.7。参考GBJ 68—84《建筑结构设计统一标准》[18],取目标可靠指标为3.2。
2.2 分项系数
2.2.1 导地线的分项系数
导地线受力的功能函数(式(8)),为线性功能函数,在已知可靠指标时,选用一般分离法得到导地线的分项系数。Z的均值和均方差为

(19)
由可靠指标β和分离函数α[19]计算得到导地线抗力,恒荷载和第i个可变荷载的分项系数分别为
γ0R=1-αRδRβγ0G=1+αTGδTGβγ0Qi=1+αTQiδTQiβ
(20)
式中:αR、αTG、αTQi——导地线抗力、恒荷载和第i个可变荷载的分离函数。
由式(20)计算得到的分项系数为均值的分项系数,而规范中的极限状态设计公式中的分项系数为标准值的分项系数。式(21)为二者的换算关系。
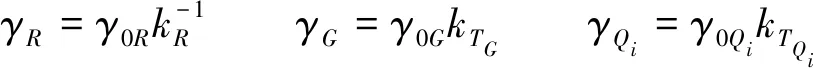
(21)
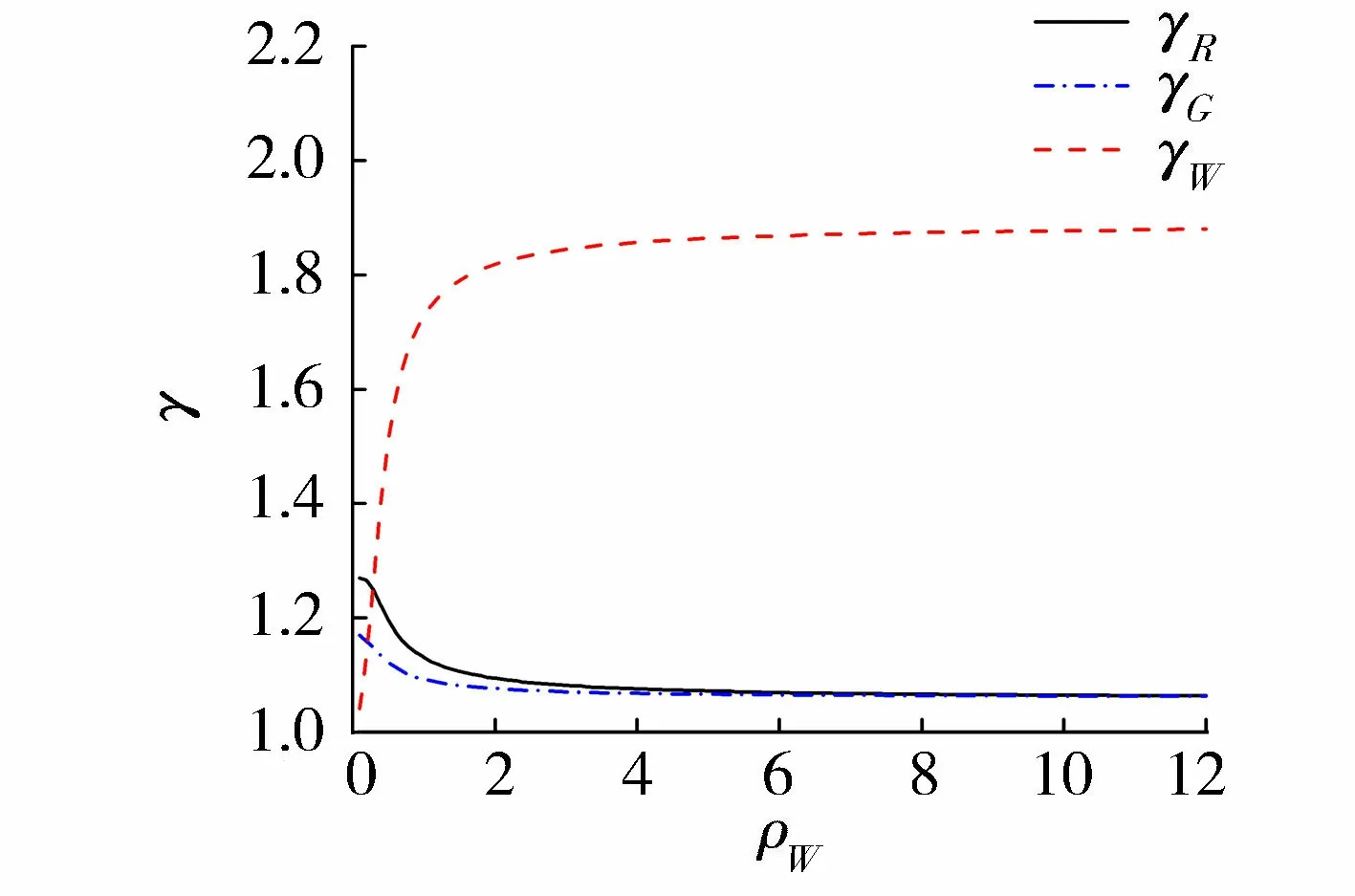
图4 导地线的分项系数Fig.4 Partial coefficient of grounding wire
考虑导地线所受荷载为恒荷载和风荷载,取可靠指标为3.2,根据式(20)和式(21),可计算得到导地线的抗力分项系数γR,恒荷载分项系数γG和风荷载分项系数γW,如图4所示。
由计算结果可知,抗力分项系数的均值为1.084,恒荷载分项系数的均值为1.072,风荷载分项系数的均值为1.828。考虑到当前对恒荷载分项系数的研究已经很成熟,参考当前规范恒荷载的分项系数取1.2,因此经过分项系数优化,建议分项系数取γR=1.1,γG=1.2,γW=1.8。
2.2.2 金具的分项系数

图5 金具的分项系数Fig.5 Partial coefficient of fittings
γ0R′=1-αR′δR′β′γ0Q3=1+αQ3δW3β′γ0Q5=1+αQ5δW5β′
(22)
式中:αR′、αQ3、αQ5——金具的抗力、导地线竖向荷载和风荷载的分离函数。
标准值分项系数为
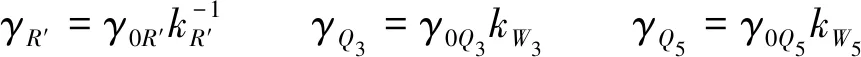
(23)
取目标可靠指标β0=3.2,考虑导地线所受荷载为恒荷载和风荷载,根据式(22)和式(23),可计算得到γR′、γQ3、γQ5,如图5所示。
由计算结果可知,金具抗力分项系数的均值为1.165,导地线竖向荷载分项系数的均值为1.062,导地线风荷载分项系数的均值为1.797。经过分项系数优化,建议分项系数取值为:γR′=1.2,γQ3=1.2,γQ5=1.8。
3 结 论
a. 通过对按现行国家标准GB 50545—2010和行业标准DL/T 5154—2012设计的导地线和金具进行可靠度校准,得到如下结果:当导地线受恒荷载与风荷载作用时,弧垂最低点和悬挂点的平均可靠指标分别为4.372和 3.968;当导地线所受荷载组合中加入覆冰荷载时,弧垂最低点和悬挂点的平均可靠指标分别为3.157和2.898。金具的平均可靠指标为3.99。
b. 取目标可靠指标为3.2,对导地线和金具的分项系数进行计算并优化,得到导地线抗力分项系数γR的均值为1.084,恒荷载分项系数γG的均值为1.072,风荷载分项系数γW的均值为1.828;金具抗力分项系数γR′的均值为1.165,导地线竖向荷载分项系数γQ3的均值为1.062,导地线风荷载分项系数γQ5的均值为1.797。
c. 若采用基于可靠度理论的设计方法,建议导地线各分项系数取γR=1.1,γG=1.2,γW=1.8;金具各分项系数取γR′=1.2,γQ3=1.2,γQ5=1.8。
