基于SBL-WVD的地震高分辨率时频分析

纪永祯,张渝悦,朱立华,李 博

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油大学(北京),北京102249)

地震波在地下传播时受吸收衰减等因素的影响,因而记录到的地震数据通常具有非稳态的特征,即地震数据的频率成分随时间变化而变化[1-2]。时频分析方法可以将时域非稳态地震数据变换到时频域,利用变换获得的频率维度描述局部频谱变化。不同的频谱变化通常可以指示不同的地质构造和油气储层特征等[3-4]。因此,时频分析方法是地震数据处理和解释中常用的重要方法技术之一,被广泛应用于储层描述和油气检测[5-6]、地质构造分析[7-8]、异常体识别[9-10]。

在过去几十年间,时频分析方法被广泛研究并应用于多种信号分析。在地震数据时频分析中,最常用的工具包括短时傅里叶变换(STFT)、连续小波变换(CWT)、Gabor变换、S变换及其变体[11-14]。然而,由于窗口函数的影响,这些线性时频分析工具通常无法兼顾时间分辨率和频率分辨率,这种限制使这些工具在特定的情况下效果不佳[15]。魏格纳威利分布(WVD)是一种双线性的时频分析方法,可以获得较高分辨率的时频分布结果[16]。然而,应用于多频率成分并存的地震数据时,WVD会受到交叉项干扰,且交叉项通常表现为高度震荡,会严重影响时频分布的精度和分辨率。一种减少甚至消除交叉项干扰的方法是利用匹配追踪等算法将地震数据分解为独立的子波分量,然后求取子波分量的时频分布,最后重建地震数据的时频分布[17-18]。此类方法有利于提高基于WVD时频分析结果的分辨率,但其对地震数据的分解需要人工控制参数的介入,容易引起人为误差,并且分辨率不足以识别薄层。

贝叶斯学习算法是TIPPING[19]提出的一种基于核函数的回归分类算法,在多个领域得到了成功的应用:WILLIAMS等[20]将稀疏贝叶斯学习算法用于视觉追踪问题;SILVA等[21]运用贝叶斯学习算法进行了文本分类工作;THAYANANTHAN等[22]将模型推广到多元输出回归问题;DEMIR等[23]将其运用于图像处理中;NYEO等[24]将该算法用于动态光散射问题研究中;YUAN等[25]将其运用于叠后地震数据的反射系数反演;JI等[26]在频率域叠前反演中初次引入该算法,获得了较好的效果。在子波分解领域,贝叶斯学习算法较匹配追踪、正交匹配追踪等具有更多优势。匹配追踪类算法属于贪婪类算法,按顺序选取构建的子波库中的原子,而贝叶斯学习算法可以通过自动相关判别选取更准确的分解子波表达式,同时可以避免“结构性误差”[27]。在含噪声情况下,由于匹配追踪类算法需要人为选定正则化参数(尽管可以参考信噪比),会引入人为误差,而贝叶斯学习算法可以通过参数的自动学习确定最优参数,无需人为设定[28]。本文通过引入基于贝叶斯学习的子波分解算法来改善子波分解时的抗噪性、分辨率和准确度,并利用更接近于地震子波的雷克子波构建子波库,提出了一种两步高分辨率时频分析方法。在输入端利用贝叶斯学习算法将获得更好的子波分解结果,而基于此的WVD时频分析方法也将具有更高的准确度和分辨率。文章首先介绍了时变雷克子波库的构建和非稳态地震数据的正演模型,然后介绍了基于贝叶斯学习算法的子波分解方法,最后介绍了基于子波分解结果和WVD的地震数据时频分析方法,通过与常规方法的比较,证实了本文方法在抗噪性、分辨率和准确度上的优势。

1 方法理论

1.1 构建时变雷克子波库

雷克子波是地震勘探中最常用的子波之一,采用不同主频、相位和中心时差的雷克子波作为构建子波库的样本。由于非稳态地震数据具有时变特征,构建子波库时也需要考虑时变特点。首先,相同主频和相位、不同中心时差的雷克子波可以写成褶积矩阵的形式:

(1)

式中:W为(n+m-1)×n的矩阵,n代表子波采样点数,m代表反射系数采样点数;wn代表子波在第n个采样点的值。将不同主频和相位的雷克子波褶积矩阵组成如下子波库:

(2)

1.2 基于时变雷克子波库构建频率域地震褶积模型

若想将时变子波库与非稳态地震数据联系起来,需要修改传统的地震褶积模型,将反射系数的定义拓展为时变子波分解系数,将非稳态地震数据写成由不同主频、相位和中心时差的雷克子波组成的时变子波库与时变子波分解系数的线性矩阵形式:

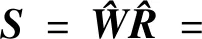
(3)

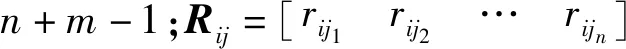
1.3 基于贝叶斯学习算法获取时变子波分解系数的估计

将时变子波库看成是稀疏核,采用贝叶斯学习算法获取子波分解系数的估计。具体步骤如下:采用常用假设,即非稳态地震数据中含有噪声n,符合零均值高斯分布,方差为σ2,那么非稳态地震数据的似然函数可以写成:

(4)

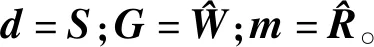
引入层状高斯分布作为每一个待估计子波分解系数的先验分布,对待估计子波分解系数进行稀疏约束[19]。先验信息如下:

(5)

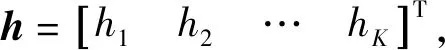
在贝叶斯框架下,待估计的子波分解系数的后验概率可以写成先验信息和似然函数的乘积[15]:

(6)

式中:

(7)

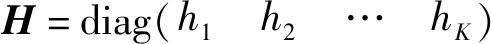
(8)

式中:Q=σ2I+GH-1GH。将(8)式估计的h和μ代回(7)式获得最终的参数估计结果。

由(8)式估计h,需采用基于最大期望算法的估计方法,该方法可以在算法进行中自适应地改变估计时的中间参数,有利于算法收敛并提高估计结果在含噪时的准确性。最大期望算法采用如下公式求解、估计h和σ2[17]。

(9)

其中,M是当前非零反射系数的个数,h与待估计的子波分解系数的均值和方差有关,σ2与数据匹配程度和稀疏度有关。至此,我们就能通过贝叶斯学习算法获得子波分解系数的估计。

1.4 利用WVD获取地震数据时频分布

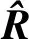
(10)

式中:Wseismic是时变地震数据的时频谱;‖Φp‖是与第p个非零系数对应的雷克子波的L2范数;WVD(·)代表常规魏格纳威利分布的计算结果。

2 应用实例

2.1 模拟数据实验

设计一个含噪声模型,测试本文方法的子波分解和抗噪能力。选取5个雷克子波作为组成无噪数据的参考子波,然后加入与信号能量一致的随机噪声,即信噪比为1。其中雷克子波的主频分别是50,30,50,40,30Hz;时间位置分别是50,65,90,105,150ms。与基于Gabor变换和匹配追踪算法的时频分析方法进行对比。图1a给出了组成模拟数据的雷克子波。图1b给出了加入噪声的模拟数据,其中,蓝色曲线为加噪后的数据,红色曲线为无噪声数据,图1b 是将图1a中子波进行线性叠加获得的。在图1b 中,由于子波的时间位置较近,无噪声数据展现了很多子波调谐效应,噪声也使得模拟地震数据更加复杂。图1c显示了本文方法获得的子波分解结果,与图1a相比,子波分解结果非常准确。图1d给出了利用匹配追踪方法获得的子波分解结果,由图1d可见,其子波分解结果不理想,单个子波的估计结果与参考子波不同且分解子波的个数也多于参考子波个数,产生了冗余信息。图1e对比了无噪数据(蓝色曲线)、本文方法重构数据(黑色曲线)和匹配追踪方法重构数据(红色曲线)。由图1e可见,本文方法获得的重构数据与原始无噪数据更加匹配,虽然匹配追踪算法的匹配程度也非常好,但其利用的子波并非完全准确,利用了更冗余的子波来重建原始数据的过程会导致后续时频分布不准确和分辨率下降。图2给出了本文方法、匹配追踪方法和Gabor变换方法得到的时频分布结果,图中白色十字标记了参考的准确时频分布位置。由图2可见,基于Gabor变换方法得到的时频分布结果分辨率较低(图2c),其分辨率一定程度上取决于窗函数的选取,但由于无法同时兼顾时间和频率分辨率,即使调节窗函数,也很难获得高分辨率的结果。对比本文方法(图2a)和匹配追踪算法(图2b)得到的时频分布结果可以看出,本文方法在有噪声的情况下仍然较好地获得了地震数据的时频分布结果;而匹配追踪算法获得的时频分布受到子波分解和噪声的影响,时频聚焦性和准确度与参考结果有一定差异。由此可见,本文方法的抗噪性能强,子波分解的准确度和分辨率高。

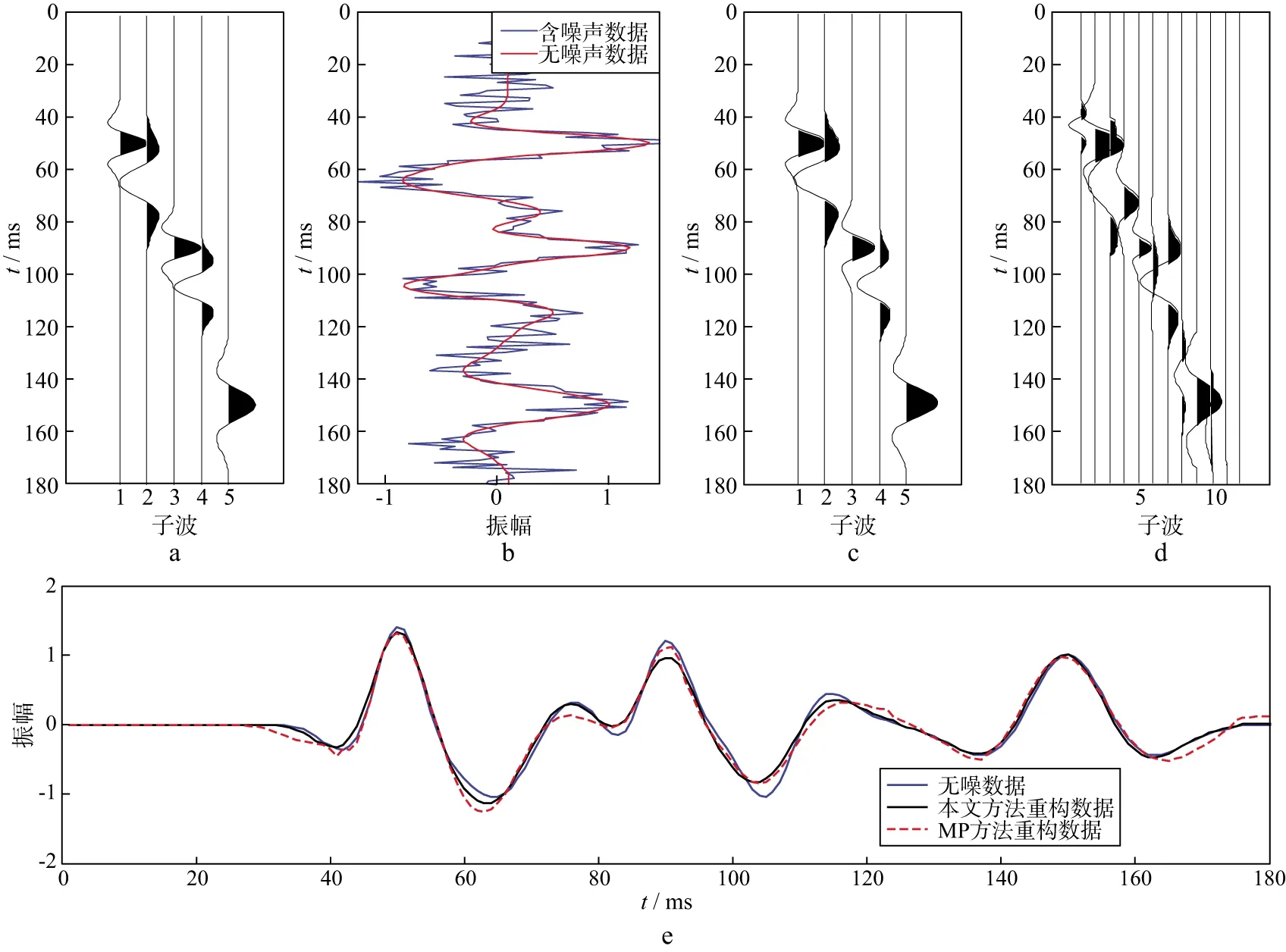
图1 模拟数据及子波分解和重构结果a 模拟数据所用的雷克子波; b 加噪声的模拟地震数据(信噪比=1); c 基于本文方法获得的子波分解结果; d 基于匹配追踪算法获得的子波分解结果; e 无噪声地震数据与重构数据的对比

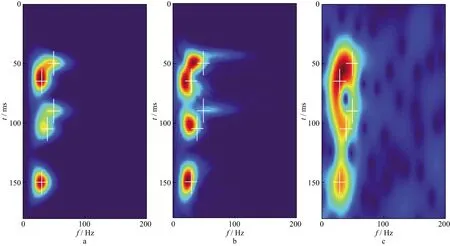
图2 3种方法得到的时频分布结果a 本文方法; b 匹配追踪方法; c Gabor变换方法

2.2 实际数据实验

实际数据实验中,首先选取井旁地震数据进行实验对比,根据测井数据的解释结果,在500ms附近有一含气储层,表现为高频衰减的特征。图3a、图3b和图3c分别给出了本文方法、匹配追踪算法和Gabor变换方法获得的井旁地震道时频谱。对比图3b和图3c中400～500ms处红色框内的时频谱可以看到,框中展现了两个时频聚焦的位置,体现了高频衰减的特征。从图3a可以清晰地看到,在红色框中实际存在4个时频聚焦的位置,在接近500ms时,时频分布展现了幅度最大的从高频向低频移动的特征。基于图3b和3c判断,含气储层存在于400～500ms处,但从图3a可以推断,含气储层应该出现在480～500ms位置。由此可见,本文方法有效提高了时频分析的分辨率和精度。另外,在时间深度800ms以下的部分,本文方法也体现了更高的分辨率,一些小层展现得比较好。

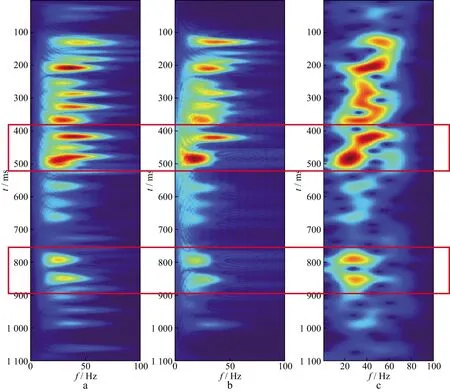
图3 3种方法获得的井旁地震道时频谱a 本文方法; b 匹配追踪方法; c Gabor变换方法

图4a、图4b和图4c分别给出了实际地震数据采用本文方法、匹配追踪算法和Gabor变换方法获得的30Hz单频切片。对比3种方法得到的单频切片可见,基于子波分解类的时频分析方法较基于时窗的Gabor方法分辨率高。对比图4a和图4b可以看出,图4b中的结果出现了比较明显的“挂面条”现象,受噪声影响,各道数据的时频分析结果不够稳定,且分辨率比图4a低,时频聚焦性也略逊于图4a。实际数据测试结果证明了采用本文方法得到的时频分析结果在分辨率、精度和抗噪性上具有一定优势,有利于提高后续基于时频分析结果的处理和解释成果的质量。然而本文方法也具有一定的局限性,从图4a可以看出,本文方法获得的时频分布的连续性仍有提高的空间。

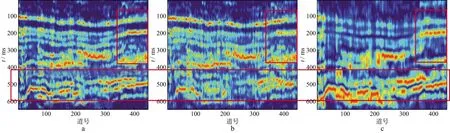
图4 3种方法获得的实际数据30Hz单频切片a 本文方法; b 匹配追踪方法; c Gabor变换方法

3 结论

本文提出了一种基于贝叶斯学习算法和魏格纳威利分布的两步高分辨率时频分析方法。首先利用贝叶斯学习算法的高精度信号分解能力,获得地震数据的子波分解结果,同时在一定程度上压制了随机噪声,再利用魏格纳威利分布的高分辨率时频分析能力获得地震数据的时频分布结果。模拟数据和实际地震数据测试结果表明,本文方法与常规基于Gabor变换和匹配追踪的时频分析方法相比,具有更高的精度和分辨率。需要注意的是,本文方法采用的子波库为雷克子波库,在地震子波与雷克子波差距较大时,该方法获得的时频分析精度将受到一定影响。下一步可以通过改进构建的雷克子波库,提高方法的适用性。