涡流渗透深度影响因素分析
2020-02-06王闯龙武美先张东利
王闯龙, 武美先, 张东利,姜 禄,佟 宇
(北方民族大学 a.电气信息工程学院;b.化学与化学工程学院;c.机电工程学院,宁夏 银川 750021)
0 引言
涡流检测(eddy current testing,ECT)是一种重要的无损检测方法[1-3],其原理是法拉第电磁感应定律,当材料表面存在缺陷时,涡流流动受到扰动,涡流传感器检测到含有裂纹的合成场(由初级场和次级场产生)信息[4-6]。由于存在集肤效应,当激励线圈在较高频率工作时,涡流主要集中在导电试件表面流动,这种效应使涡流传感器对浅裂缝检测较灵敏,但对深层裂纹的识别能力较低[7-11]。国内外许多学者提出了改进方法。文献[12]设计了新型缺陷探测系统,可提高检测的稳定性。文献[13]通过增加磁环,制作了新型探头,提高了检测能力。文献[14]设计了基于数字信号处理的涡流检测系统,提高了检测的抗干扰能力。文献[15-16]用磁通门磁强计设计新型涡流线圈,提高了渗透深度。但传统涡流检测线圈渗透深度的影响因素问题并未得到彻底解决。文献[17]提出涡流密度不仅与涡流线圈激励频率有关,还与线圈尺寸等其他因素有关。
本文使用ANSYS有限元软件,分析线圈外径、高度、匝数、提离以及激励频率等因素对涡流密度的影响,提取沿试件厚度方向的涡流密度。以试件表面涡流密度为基准值,对提取的涡流密度进行归一化处理,进一步分析了各个因素对涡流渗透深度的影响。
1 数值计算模型
试件涡流密度值降低到表面密度的1/e(37%)时的渗透深度为标准渗透深度[7],在仿真计算过程中,通过提取试件内涡流密度变化曲线,可以得到相应的渗透深度。为了方便获取涡流密度曲线对应的标准渗透深度值,将涡流密度曲线进行归一化(归一化涡流密度曲线是指将涡流密度曲线上的所有数据除以其最大值得到的曲线),归一化涡流密度曲线横坐标值是0.37时所对应的纵坐标值为涡流的标准渗透深度。
如图1所示,建立参数化模型,分析渗透深度的影响因素。将线圈放置在SUS304不锈钢制成的试件(200 mm×200 mm×50 mm)上方。线圈的外径为Ro,内径为Ri,高度为hc,匝数为N,提离为D。
2 渗透深度的影响因素
普通圆形涡流线圈在实际使用过程中,通常加载正弦交流电流。合适的激励频率可以有效准确地识别并分离出各种影响因素,当频率增高时,集肤效应也随之明显,线圈识别缺陷的灵敏性会急剧降低,因此,合适的激励频率对检测缺陷至关重要。涡流线圈结构尺寸对涡流场的影响具体表现为:线圈外径影响周围磁场的分布;线圈匝数影响线圈电感量的大小;线圈高度与检测系统的灵敏度、分辨率有关;提离效应影响线圈阻抗的大小。

图1 参数化模型
2.1 线圈外径的影响
如图1所示,线圈的提离D=0.5 mm,激励频率f=10 kHz。保持线圈的内半径Ri=8 mm不变,外半径Ro分别为10 mm、15 mm和20 mm,线圈匝数N=140匝,线圈高度hc=8 mm,研究线圈外径的影响。
图2为归一化前后涡流密度与线圈外径Ro的关系。图2中,试件厚度为沿板厚方向的厚度。如图2a所示,保持线圈内径不变,当线圈外径逐渐增大时,涡流密度增大。如图2b所示,线圈外径越大,其渗透深度越大。

(a) 归一化前涡流密度与线圈外径Ro的关系 (b) 归一化后涡流密度与线圈外径Ro的关系
图2 归一化前后涡流密度与线圈外径Ro的关系
2.2 线圈高度的影响
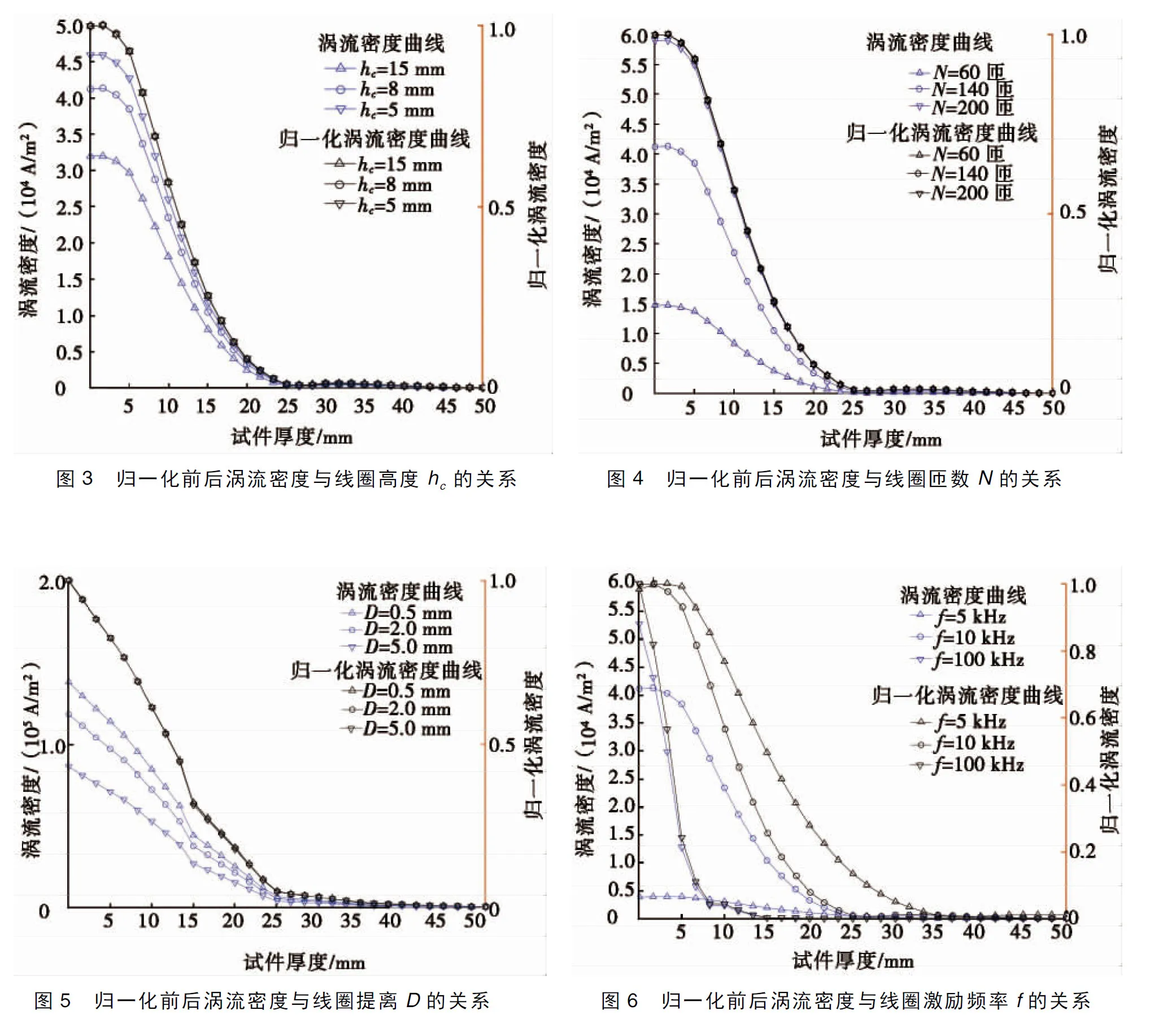
选择内径Ri=8 mm,外径Ro=15 mm的线圈进行仿真计算,并分析其结果。取线圈高度hc为5~15 mm,分析其对渗透深度的影响,结果如图3所示。由图3可以观察到线圈高度和涡流密度之间的比例关系,归一化密度曲线也较为密集。由图3可知:涡流的渗透深度较为接近,线圈高度对渗透深度的影响较小。
2.3 线圈匝数的影响
研究线圈匝数对渗透深度的影响,匝数分别为60匝、140匝和200匝。Ri和Ro分别为8 mm和15 mm。其他参数设定值与2.1节相同。图4为归一化前后涡流密度与线圈匝数N的关系。如图4所示,渗透深度不受线圈匝数变化的影响。
2.4 提离的影响
提离是指线圈底部到试件表面的距离,在涡流检测中是一个重要的影响因素。在仿真分析过程中,保持其他参数不变,线圈提离分别为0.5 mm、和2.0 mm和5.0 mm。图5为归一化前后涡流密度与线圈提离D的关系。如图5所示,当线圈提离增大时,激励线圈在试件表面产生的涡流密度减小,但是并不能改变其渗透深度;较大提离在试件内部产生的涡流密度越来越小。在实际应用中,很少采用较大提离,因为较大提离会使检测信号显著下降、信噪比降低。
2.5 激励频率的影响
为了研究激励频率对渗透深度的影响,激励线圈的激励频率分别取5 kHz、10 kHz和100 kHz,其他参数配置与上文相同。图6为归一化前后涡流密度与线圈激励频率f的关系。由图6可知:当激励频率明显降低时,渗透深度发生显著的变化。在较高频率激励时,涡流主要集中在密度极大的试样表面附近,并沿试件厚度方向急剧降低;与此相反,在较低频率激励时,尽管表面的涡流密度较小,但在试件内部的涡流密度衰减较慢。因此,低频条件有利于检查导电材料中的较深裂缝。
3 渗透深度影响因素的验证
3.1 试验系统
为了验证不同因素对渗透深度的影响,设计加工了SUS304不锈钢试件,如图7a所示,不锈钢尺寸为1 350 mm×350 mm×200 mm,电导率为σ=1.43×106S/m,相对磁导率为μr=1。在不锈钢试件上均匀加工3道通槽,宽度均为1 mm,深度分别为5 mm、10 mm和15 mm。
涡流检测系统如图7b所示,为了保证检测的准确性,将涡流线圈(检测线圈和激励线圈)安装在三维扫查台的扫查臂上,保持检测探头与试件上表面水平且提离固定。三维扫查台以恒定速度在不锈钢试件表面垂直于裂纹分布方向进行扫描。接收端使用爱德森涡流检测仪EEC-2004作为采集系统,常规圆形涡流传感器作为采集端和激励端,对分布在不锈钢试件上不同渗透深度的人工裂纹依次进行检测。

3.2 结果验证
为了充分验证有限元仿真结果的正确性,试验中使用的参数与仿真参数一致。
3.2.1 线圈外径的影响
试验使用激励线圈内径Ri=8 mm;外径分别为Ro1=10 mm,Ro2=15 mm;激励频率为f=10 kHz;提离为D=1 mm;匝数N=140匝。
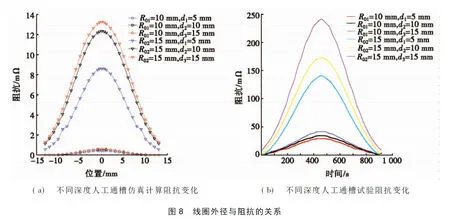
图8为线圈外径与阻抗的关系。图8a为在不同外径时仿真计算不同深度的人工通槽产生的阻抗结果,当人工通槽深度相同时,线圈外径越大,阻抗越大;当线圈外径相同时,人工通槽深度越大,阻抗越大。 图8b为与仿真计算相同参数下试验所得结果(下同),由图8b可知:试验结果与仿真结果一致。分别提取激励线圈外径不同时检测线圈在通槽为5 mm、10 mm和15 mm对应阻抗的最大值Z0、Z1和Z2,并计算10 mm和15 mm相对于5 mm人工通槽阻抗变化倍数Z1/Z0、Z2/Z0。由试验和仿真计算结果可得:当人工通槽深度相同时,线圈外径越大,检测结果的阻抗越大;当线圈外径相同时,人工通槽深度越深,所产生的阻抗结果越大。因此,线圈内径相同,外径越大,检测线圈的阻抗变化越大,有利于深裂纹的检测。
3.2.2 线圈匝数的影响
试验使用线圈内径Ri=8 mm,外径Ro=15 mm,高度hc=8 mm,线圈匝数分别为140匝和250匝,其他参数保持不变。图9是线圈匝数与阻抗的关系。由图9a可知:线圈匝数相同时,人工通槽深度越大,检测线圈产生的阻抗越大;但人工通槽深度相同时,线圈匝数的变化几乎不影响检测线圈阻抗信号的大小。图9b是仿真参数相对应的试验结果,与仿真计算结果一致。因此,线圈匝数基本不影响涡流的渗透深度,对检测线圈的阻抗影响较小。

(a) 不同深度人工通槽仿真计算阻抗变化 (b) 不同深度人工通槽试验阻抗变化
图9 线圈匝数与阻抗的关系
3.2.3 线圈高度的影响
试验使用线圈内径Ri=8 mm,外径Ro=15 mm,高度分别为hc1=8 mm和hc2=15 mm,其他参数保持不变。由于激励线圈的高度发生变化,为了减小线圈匝数对结果造成的影响,线圈的绕制匝数分别为140匝和250匝。图10为线圈高度与阻抗的关系。如图10a所示,线圈高度越大,检测线圈的阻抗信号越大;线圈高度相同,人工通槽深度越大,检测线圈阻抗越大;但是,通过提取人工通槽处阻抗的最大值Z0、Z1和Z2,并计算阻抗变化倍数Z1/Z0、Z2/Z0,得出相同深度人工通槽在线圈高度不同时,阻抗的变化倍数是相同的。图10b为仿真参数相对应的试验结果,其变化规律、阻抗变化倍数结果与仿真计算结果一致。因此,激励线圈高度改变检测信号的阻抗大小,但是对渗透深度的影响较小。

(a) 不同深度人工通槽仿真计算阻抗变化 (b) 不同深度人工通槽试验阻抗变化
图10 线圈高度与阻抗的关系
3.2.4 提离的影响
试验使用线圈内径Ri=8 mm,外径Ro=15 mm,高度hc=8 mm,提离D1=1 mm、D2=5 mm,其他参数保持不变。图11为线圈提离与阻抗的关系。如图11a所示,线圈提离增大时,检测线圈的阻抗信号急剧减小;相同提离时,人工通槽深度越大,阻抗越大。图11b是与仿真计算参数相同时的试验结果,其变化规律与仿真计算结果一致。但是在实际检测过程中当提离增大时,阻抗信号的信噪比也会降低,由于这种现象会造成涡流线圈对裂纹的识别度显著下降,所以在实际应用中提离变化对检测结果的准确性有很大影响。
3.2.5 激励频率的影响
试验使用线圈内径Ri=8 mm,外径Ro=15 mm,高度hc=8 mm,激励频率分别为f1=1 kHz,f2=10 kHz,其他参数保持不变。图12为激励频率与阻抗的关系。分别提取激励频率为1 kHz和10 kHz时,各个裂纹处的最大阻抗值Z0、Z1和Z2,并计算阻抗的变化倍数Z1/Z0、Z2/Z0。由图12a可知:同一激励频率,不同深度的裂纹产生的阻抗变化不同,裂纹深度越深,阻抗越大;同一深度裂纹,激励频率越高,阻抗越大;通槽的深度变化相同时,激励频率越低,阻抗变化倍数越大。图12b是与仿真计算参数相同时的试验结果,其变化规律同仿真计算结果一致。较低激励频率有利于识别深层裂纹缺陷,但是激励频率太低时,检测信号的阻抗幅值会急剧下降,不利于检测,因此,选择合适的激励频率对涡流检测至关重要。
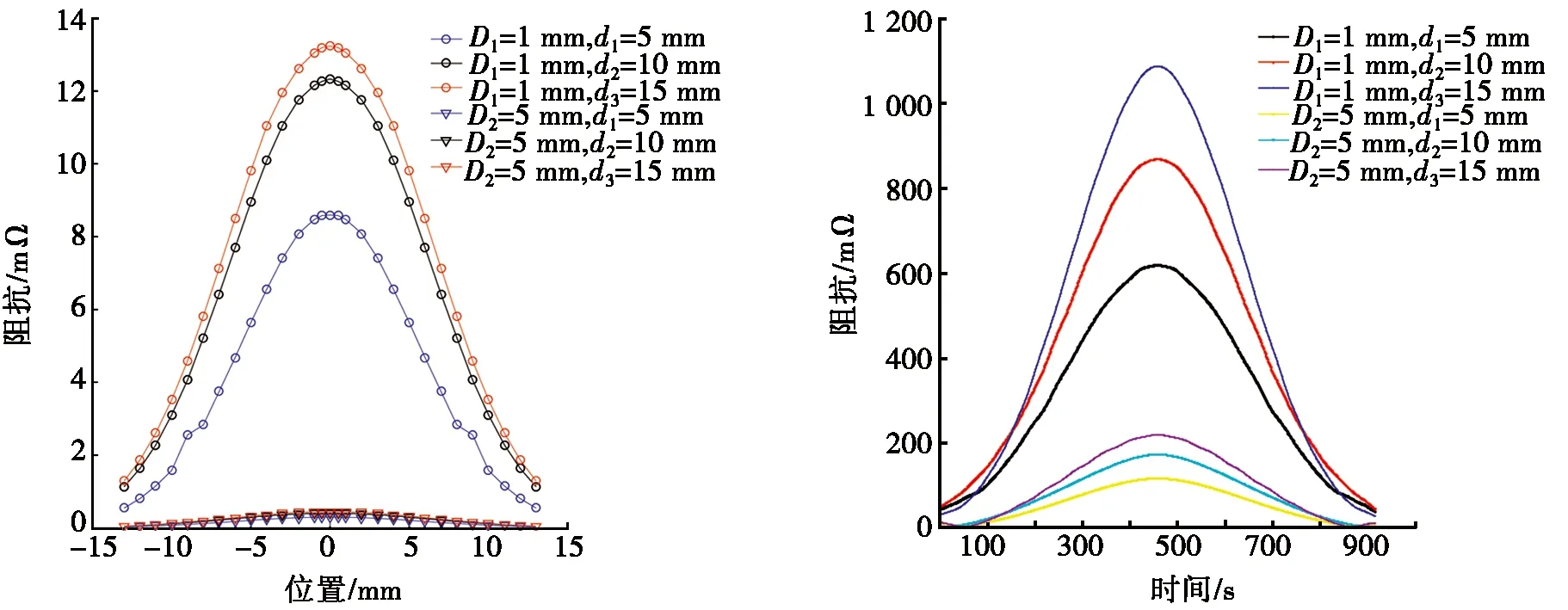
(a) 不同深度人工通槽仿真计算阻抗变化 (b) 不同深度人工通槽试验阻抗变化
图11 线圈提离与阻抗的关系

(a) 不同深度人工通槽仿真计算阻抗变化 (b) 不同深度人工通槽试验阻抗变化
图12 激励频率与阻抗的关系
4 结束语
通过仿真计算与试验验证,激励频率和线圈外径有助于提高渗透深度,提离影响涡流线圈的信噪比,其他因素对渗透深度影响较小。本文可为涡流线圈设计和导电材料深层裂纹的检测提供指导。
