基于局部火灾情况下冷弯薄壁型钢货架立柱稳定性研究
2020-02-06戴柳丝
任 重,张 鹏,戴柳丝
(上海大学 土木工程系,上海 200444)
近年来,随着制造业和物流业高速发展,仓储体系需求也越来越大,同时对钢货架安全性、实用性、经济性也提出了更高要求。冷弯薄壁型钢由于具有自重轻、强度高、节能环保、便于组装拆卸和高效空间利用率等优势被广泛应用于钢货架、钢框架、桁架等结构中。但是由于冷弯薄壁型钢立柱截面的复杂化以及孔洞形式多样化,货架立柱轴压性能极易受到局部屈曲、畸变屈曲、整体屈曲及其各屈曲间相互作用[1]的影响。为完善我国冷弯薄壁型钢构件设计方法,国内学者对常温下冷弯薄壁型钢构件稳定性进行大量研究[2-8]并将其成果写入《冷弯薄壁型钢结构技术规范》中[9]。但是众所周知,钢材是一种不耐高温的材料。由于钢材热传导率高,一旦发生火灾,未加保护的钢构件在高温作用下,屈服强度、极限强度和弹性模量都会迅速下降[10-12],从而严重削弱其受力性能。欧洲、澳洲等地学者对于冷弯薄壁型钢构件研究起步较早,对常温[13-16]和均匀高温下[17-20]冷弯薄壁型钢构件已经进行大量研究,并据此形成了较完善的设计方法。然而,在实际火灾中,构件及其周围空气温度分布是不均匀的[21-24],并且这种温度梯度会对冷弯薄壁型钢构件的破坏模式造成严重影响[23]。另外,冷弯薄壁构件的设计方法主要为有效宽度法和直接强度法;由于有效宽度法并不适用于连续开孔且截面复杂的构件,通常采用直接强度法对其承载力进行预测[25]。直接强度法由于具有简单高效的特点而被澳洲冷弯薄壁型钢结构设计规范和北美冷弯型钢结构设计规范采纳,但是原始的DSM设计公式并没有考虑到温度梯度的影响。如果忽略温度梯度而采用均匀高温下的结构设计方法将低估冷弯薄壁型钢承载力,从而降低其经济性。但是局部火灾下冷弯薄壁型钢构件设计方法尚未完善,加之其具有很高的热传导率和复杂的初始缺陷,冷弯薄壁型钢构件在局部火灾下受力性能更难以预测。因此,冷弯薄壁型钢货架立柱在局部火灾下的稳定性研究具有重要的理论意义。
1 有限元模型的建立
本文采用有限元分析软件ABAQUS对货架立柱在局部火灾下的受力性能进行数值分析,如图1所示。有限元模型中的材料本构关系设为理想弹塑性模型,在欧洲规范EN 1993-1-2的基础上计算出高温下冷弯薄壁型钢的材料属性,如表1所示。所有模型的边界条件均为两端铰接(底部为U1=U2=U3=UR3=0,顶部为U1=U2=UR3=0)。为了实现轴向加载,首先在立柱顶部截面形心处设置一个参考点RP-1,然后将顶部截面与参考点RP-1进行动态耦合(Kinematic coupling),并将RP-1作为加载点以实现轴向加载。与立柱顶部做法类似,立柱底部也需要在底部截面形心处设置参考点RP-2,并将底部截面与参考点RP-2动态耦合。所有的有限元分析模型都包含三个部分:
1) 热传递分析。以欧洲规范EN 1991-1-2的局部火源模型为基础,假设火焰高度为立柱高度的三分之一,火源的最大热释放率与大型商场类似为250 kW/m2,且达到最大热释放率的时间为150 s.与现有组合墙传热结果不同[26],局部火灾情况下假设火源在货架立柱底部,因此忽略立柱截面方向上的温度梯度,只考虑沿立柱高度方向上的温度不均匀分布。热传递分析模型中的单元采用四结点传热四边形壳单元(DS4),可以准确高效地用于局部火灾情况下的温度场分析。

图1 局部火灾下货架立柱有限元分析模型
2) 特征值屈曲分析(Linear Perturbation).在第一步的基础上,采用四结点曲面薄壳单元(S4R)对货架立柱在局部火灾情况下的轴压稳定性进行分析,并得到各模态下临界荷载、屈曲模态及位移。
3) 材料几何非线性分析(Riks).在第一步的基础上将特征值屈曲分析结果中第一屈曲模态位移的L/1 000作为货架立柱的初始缺陷导入并进行材料几何非线性分析。单元采用S4R.

表1 高温下冷弯型钢的材料属性
2 有限元模型的验证及参数分析
由于局部火灾下立柱试验较少,为保证数值分析的准确性,分3个部分对有限元模型进行验证。
2.1 热传递分析
利用CRAVEIRO et al[27]的试验数据进行验证,选取构件C_PP_30LL_K1-3作为验证对象。以试验中的高温炉内温度作为有限元模型的环境温度,构件周围环境通过热对流将热量传递到构件使其温度升高。由于试验中a,b和c的升温曲线基本一致,故选择测点b的结果进行验证。试验与有限元中构件同一位置(构件中部腹板处测点b)的升温曲线如图2所示,较好的吻合性说明热传递分析结果具有可靠性。
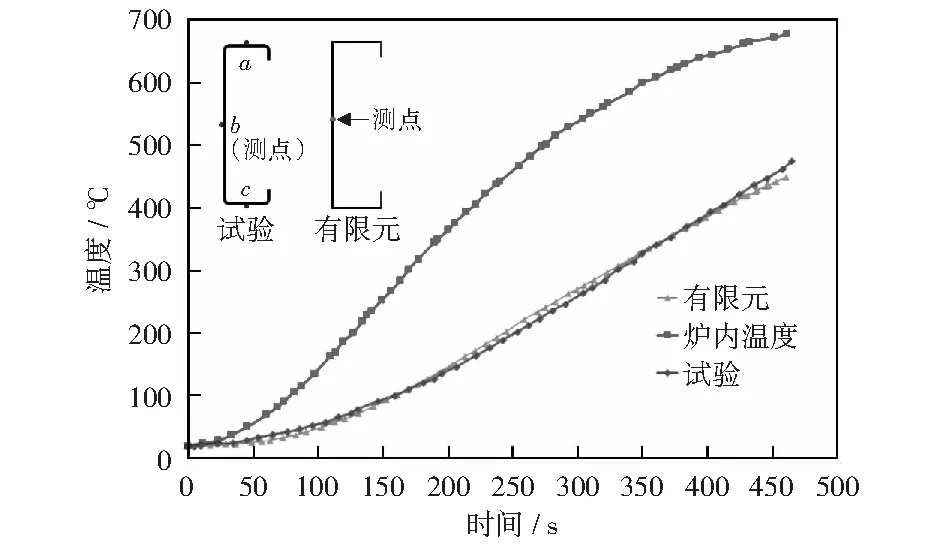
图2 温度场分析与现有的热传递试验数据对比
2.2 特征值屈曲分析
利用YOUNG et al[28]的试验结果验证临界荷载、半波长个数和屈曲模态,将第一阶模态下有限元分析结果与试验结果进行对比,如表2所示,有限元分析结果与试验结果吻合较好。
2.3 材料几何非线性分析
利用ZHAO et al[1]的试验数据验证轴压冷弯薄壁型钢货架立柱的极限荷载,结果如表3所示,对比可得有限元分析的结果与试验结果基本一致。综上可知,所建的模型能准确预测货架立柱在局部火灾情况下的受力性能。
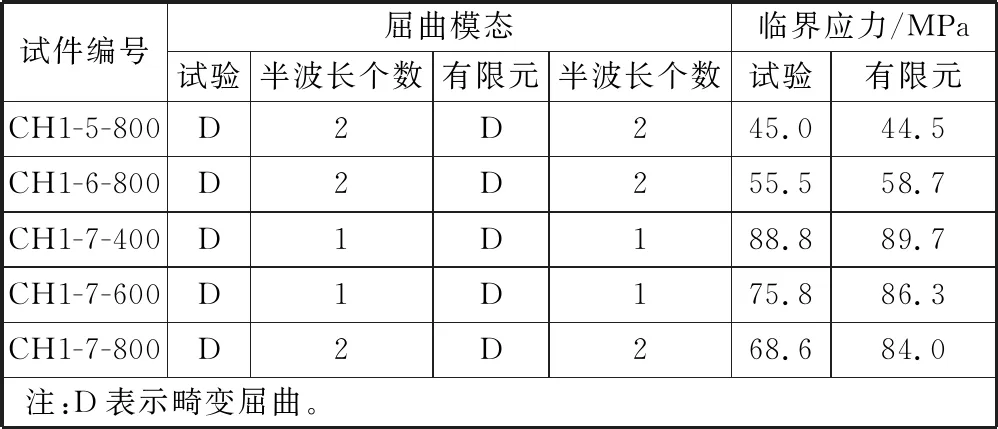
表2 特征值屈曲分析结果与试验结果对比

表3 材料几何非线性分析结果与试验结果对比
本文采用已验证的数值分析方法对180个局部火灾下货架立柱进行数值分析,立柱参数包括8种异型截面、4种构件长度、5种最高温度,结果如表4
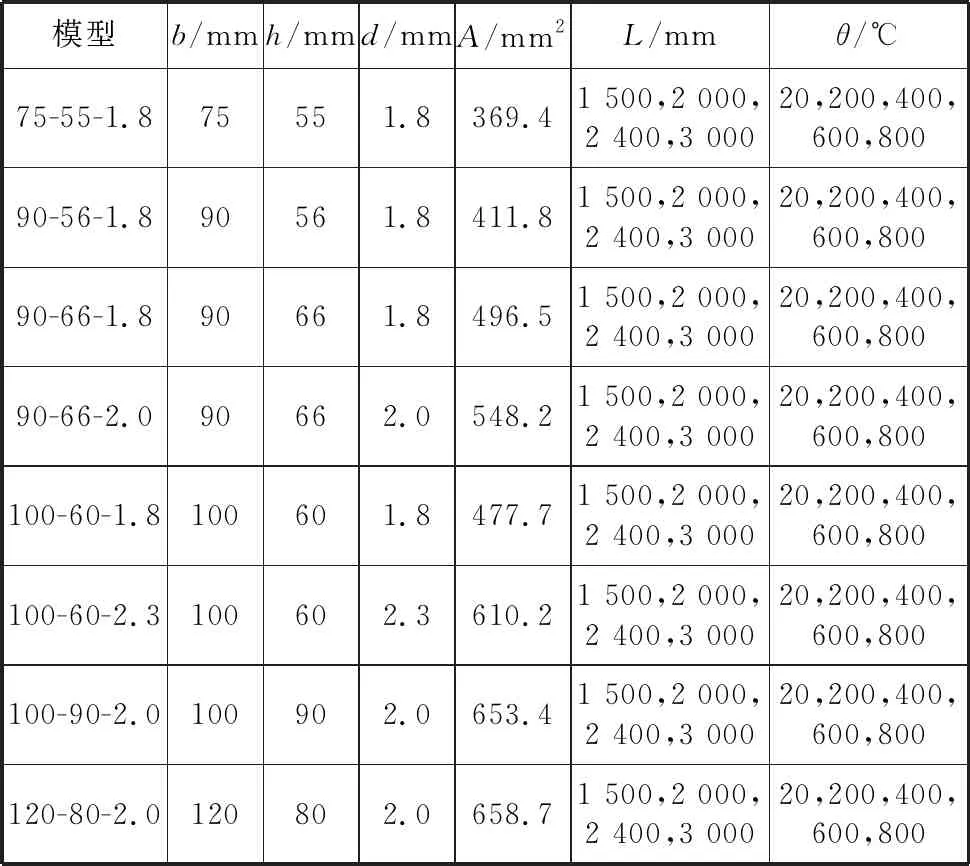
表4 模型的几何参数和最高温度
所示,其几何特征如图3所示。所有模型采用统一的命名方式,如:100-60-1.8-2000-400代表构件的腹板宽度b为100 mm,翼缘高度h为60 mm,截面厚度d为1.8 mm,构件长度L为2 000 mm,底部的最高温度θ为400 ℃.
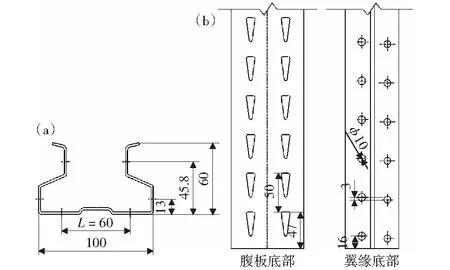
图3 (a) 截面几何参数(孔洞的相对位置已被标记),(b) 孔洞的尺寸
3 有限元分析结果
3.1 热传递分析结果
图4为75-55-1.8-2000立柱在局部火灾影响下,不同时间点立柱温度沿高度方向的分布情况(a)及不同高度点的升温曲线(b).火灾发生初期火源热释放率较低,立柱底部从20 ℃升至200 ℃大约需要56 s,由于钢材的导热率较高,立柱底部温度从200 ℃升至800 ℃只需要大约69 s.由图4可知,当冷弯薄壁型钢货架立柱底部发生局部火灾时,立柱存在明显的温度梯度,并且局部火灾情况下火源对立柱底部的影响非常明显,而对于立柱上部的影响较小。因此采用构件整体升温的设计方法对货架立柱进行设计将会低估其轴压承载力,从而降低冷弯薄壁型钢构件的经济性。
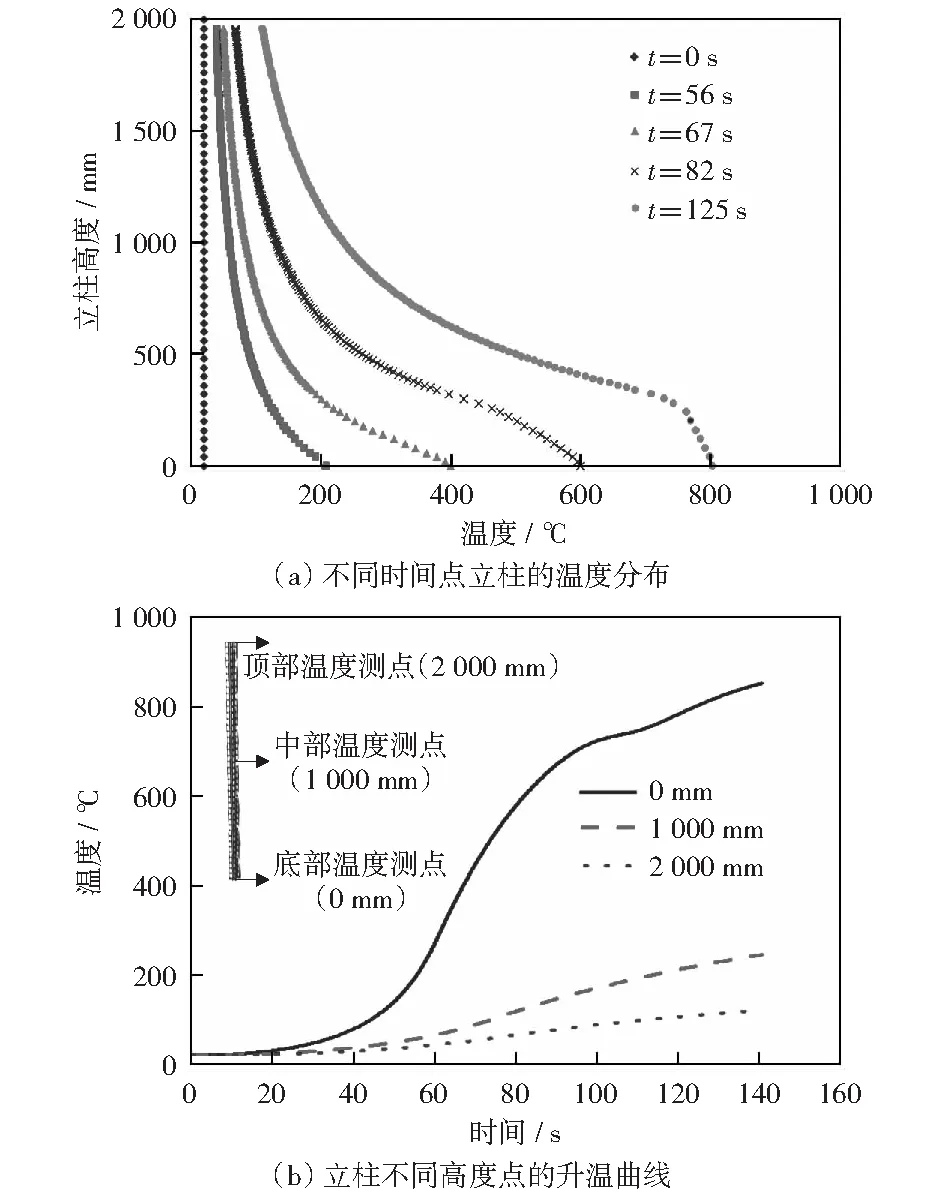
图4 75-55-1.8-2000的热传递分析结果
3.2 特征值屈曲分析结果
特征值屈曲分析中第一阶模态的临界荷载(以下简称临界荷载)是立柱稳定性的体现,临界荷载较大说明其稳定性较好。由图5-图7可得,货架立柱的稳定性受温度、截面和构件长度影响较大。由于弹性模量随着温度升高而减小,因此立柱的临界荷载随温度升高而下降,特别是600 ℃以后出现大幅度降低。通过20 ℃下1 500 mm长度的3种截面(75-55-1.8,90-56-1.8和100-60-1.8)轴压承载力(分别为88.7 kN,104.6 kN和152.9 kN)对比可知,增大立柱截面可以有效增强其稳定性。减少立柱的计算长度可以增强其稳定性,但是当立柱长度较大(3 000 mm)时,温度对其临界荷载的影响相对较小。

图5 不同温度下75-55-1.8截面的临界荷载对比

图6 不同温度下90-56-1.8截面的临界荷载对比
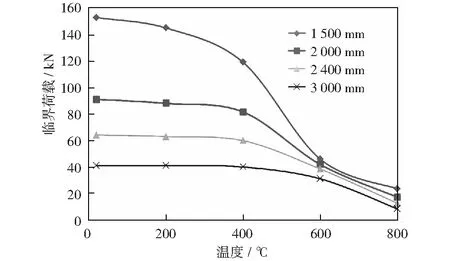
图7 不同温度下100-60-1.8截面的临界荷载对比
图8为各种截面货架立柱在高温下的临界荷载折减系数对比图,其中pcr,1,θ代表温度θ℃下立柱的临界荷载,pcr,1,20代表20 ℃下立柱的临界荷载。由图8可以看出不同长度的各种截面在不同温度下的临界荷载随长度变化呈带状分布,pcr,1,θ/pcr,1,20随立柱长度增加而增大,且离散性较小。

图8 不同温度下临界荷载的折减系数
3.3 几何非线性分析结果
采用弧长法可以较准确计算立柱轴压承载力,并且可以考虑材料几何非线性效应和初始缺陷的影响。在弧长法分析结果中得到的是弧长-LPF(load proportionality factor)曲线,将LPF与荷载施加值相乘再与立柱的轴向位移关联,形成位移-荷载曲线。位移-荷载曲线可以很方便准确地表示受压立柱的轴向变形能力及其荷载情况。对不同长度的75-55-1.8截面立柱进行常温下弧长法分析并选取荷载最大点的荷载值为立柱的轴压承载力,结果如图9所示,长度增加不仅会降低立柱的轴压承载力,还会影响最大荷载所对应的轴向位移值。为了探究局部高温对不同长度立柱轴压承载力的影响,分别分析长度为1 500,2 000,2 400和3 000 mm的75-55-1.8截面立柱在不同温度下的承载力,结果如图10-图13所示,局部火灾对货架立柱轴压承载力产生不同程度的不利影响。当立柱长度为1 500 mm时,局部高温对其轴压承载力影响较明显;当立柱长度为2 000 mm时,200 ℃的局部高温对其轴压承载力的影响较小;当立柱长度为2 400 mm时,200 ℃的局部高温几乎不影响立柱轴压承载力;当立柱长度为3 000 mm时,200 ℃的局部温度几乎不影响其轴压承载力并且400 ℃的局部高温对其轴压承载力产生的影响也较小。
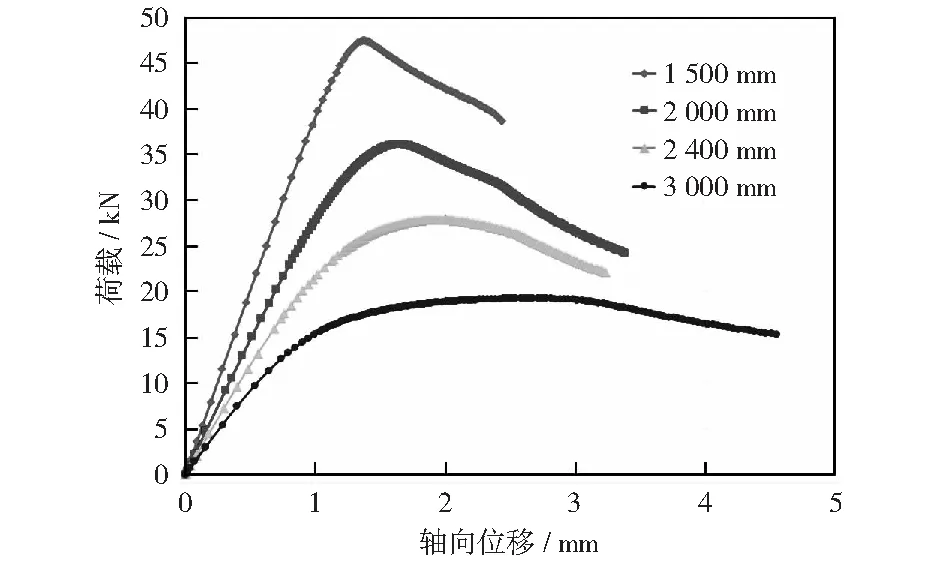
图9 常温下75-55-1.8截面的承载力对比
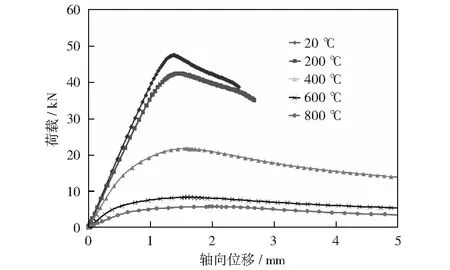
图10 不同温度下75-55-1.8-1500的承载力对比
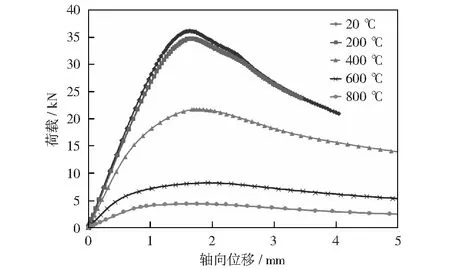
图11 不同温度下75-55-1.8-2000的承载力对比
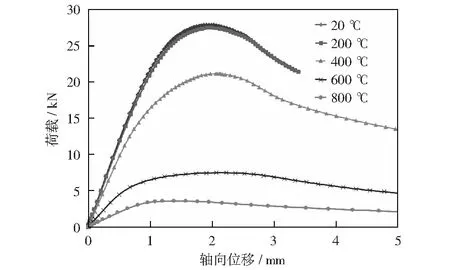
图12 不同温度下75-55-1.8-2400的承载力对比

图13 不同温度下75-55-1.8-3000的承载力对比
立柱的破坏模式对其轴压承载力有较大的影响。为了更准确分析立柱破坏模式,以位移-荷载曲线最高点的后一个点作为破坏模式的判断依据。图14-图18为75-55-1.8-2000立柱在不同温度下的Mises应力云图和屈曲截面变形图(虚线是初始截面,实线为变形后截面)。由图14可知,局部火灾对立柱的应力分布有重要的影响,20~400 ℃时立柱的应力最大值分布在立柱中部,而当温度达到600 ℃和800 ℃时立柱的底部(受火处)出现了应力的集中。局部高温导致立柱底部的应力集中不仅仅削弱了其轴压承载力而且还改变了其破坏模式,如温度为20~400 ℃时立柱的破坏模式为整体屈曲(FB),当温度为600 ℃时立柱的破坏模式变成了整体与局部相关屈曲(FB+LB),当温度达到800 ℃时其破坏模式变成了整体-局部-畸变相关屈曲 (FB+DB+LB)(为了便于观察破坏模式而对模型的变形图进行放大3倍处理)。总体来说,由于局部高温造成局部材料属性的削弱从而导致立柱底部应力集中和改变了破坏模式进而严重影响其轴压承载力。

图14 75-55-1.8-2000-20的破坏模式(FB)

图15 75-55-1.8-2000-200的破坏模式(FB)
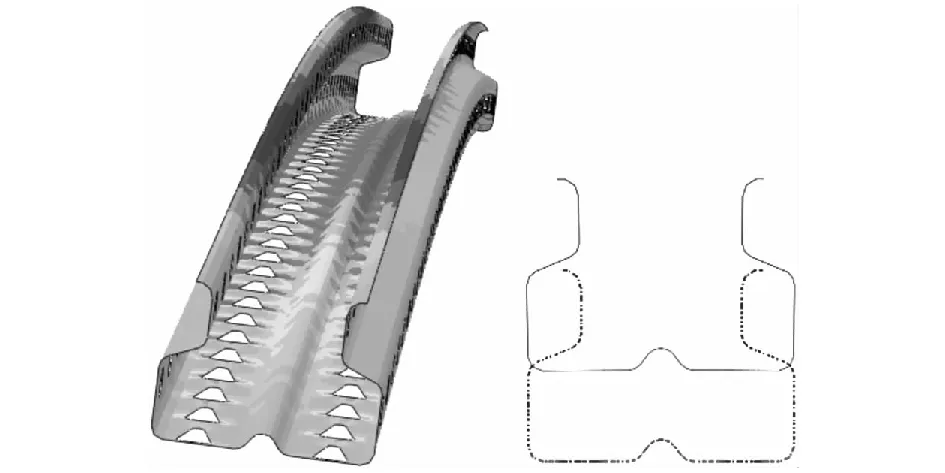
图16 75-55-1.8-2000-400的破坏模式(FB)

图17 75-55-1.8-2000-600的破坏模式(FB+LB)

图18 75-55-1.8-2000-800的破坏模式(FB+LB+DB)
4 局部火灾下冷弯薄壁型钢货架立柱DSM修正
由于研究的立柱为长柱(1 500~3 000 mm),破坏模式以整体屈曲为主,畸变屈曲和局部屈曲较少,所以不修正其DSM设计曲线。选取破坏模式为整体屈曲的立柱分析结果对原始的整体屈曲DSM设计曲线进行修正。由于原始的DSM设计公式并未考虑温度梯度的影响,无法用于预测局部火灾下的货架立柱轴压承载力,如图19所示,原始的整体DSM设计曲线对于立柱底部温度为20 ℃和200 ℃的轴压承载力可以较好地预测,但是对于立柱底部温度在400 ℃以上时无法合理预测其轴压承载力,尤其是局部高温为800 ℃时。图19和图20中的pu代表有限元分析结果中立柱的最大荷载。py=Fy×Anet,Fy为常温下材料的屈服强度,Anet为立柱的净截面面积(假设所有孔洞在同一截面上所计算的净截面面积)。λc为立柱的长细比,pcr,1,20为20 ℃下特征值屈曲分析结果中第一阶模态的临界荷载。

图19 局部火灾下货架立柱结果与原始整体DSM曲线对比
由于原始的设计曲线预测的局部火灾下货架立柱轴压承载力偏大,为了更准确地预测局部火灾下冷弯薄壁型钢货架立柱的轴压承载力,基于原始DSM整体设计曲线提出一条适用于局部火灾下此类立柱的修正设计曲线(800 ℃),如图20所示。通过修正DSM设计曲线可知,采用统一高温模型计算结果将会过于保守(如整体温度为800 ℃时材料的屈服强度折减到常温屈服强度下的0.07倍,如表1,即py,800=0.07py,20,而修正曲线只需要降到常温屈服强度的0.4倍,即py,800=0.4py,20,如图20).
5 结论
采用已验证的有限元模型对不同长度、不同截面和不同局部高温下的冷弯薄壁型钢货架立柱构件进行稳定性分析,得出以下结论:
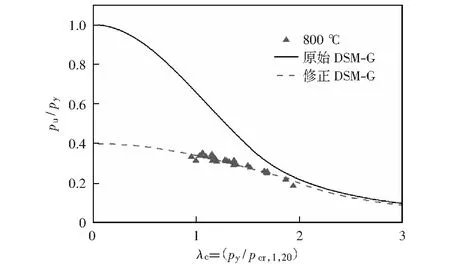
图20 局部火灾下立柱DSM修正与原始DSM曲线对比(整体屈曲)
1) 冷弯薄壁型钢货架立柱在遭受底部火灾时,最高温度出现在立柱底部,且构件的温度沿长度方向会呈现出非线性变化。
2) 由冷弯薄壁型钢货架立柱的临界荷载对比结果可以得出,温度、截面尺寸和立柱长度是影响立柱稳定性的三大主要因素。
3) 局部火灾不仅对冷弯薄壁型钢货架立柱的轴压承载力有不同程度的影响,还可能使货架立柱的破坏模式从整体屈曲变成整体-局部相关屈曲或者整体-局部-畸变相关屈曲。
4) 冷弯薄壁型钢货架立柱的轴压承载力随着局部温度的升高而逐渐降低,并且当立柱长为1 500 mm时,温度对其轴压承载力的影响相对较大,而当立柱长度为3 000 mm时,温度对其轴压承载力的影响相对较小。
5) 基于均匀高温的原始DSM设计曲线会低估局部火灾情况下冷弯薄壁型钢货架立柱轴压承载力,而基于常温的DSM设计曲线预测的立柱轴压承载力结果偏大。
本文提出适用于整体屈曲的修正DSM设计曲线,能较精确地对局部火灾下(800 ℃)货架立柱的轴压承载力进行预测。
