基于Adaptive Lasso的股票指数跟踪问题研究

侯红卫，谢 仪

(1.太原理工大学 数学学院，太原 030024；2.中国人民银行 乌鲁木齐中心支行，乌鲁木齐 830000)

投资者进行股票投资最直接的动机是获得理想回报，故而投资决策的目标是收益的最大化。然而，收益和风险是正相关的，股市的波动一方面带来了投资收益，另一方面也带来了很高的投资风险，二者互相依存。我国的证券市场近年来一直处于高速发展过程中，但其系统性风险依然很大，投资者一直在寻求能够获得稳定收益的方法，尤其是当指数化基金、股指期货、ETF等衍生产品的不断推出，指数化投资被越来越多的人所关注。指数跟踪作为指数化投资的具体管理形式，可以有效地指导股指期现套利、指数投资产品的设计等[1]。

股票指数跟踪，是指用一定方法构建投资组合以复制和跟踪某一市场指数为目标，来获得与之相同的市场平均收益。由于其分散化、被动式管理等优点，不但可以充分消除系统风险，还可以大大降低交易成本。因此，如何构建一个合理的股票投资组合并使其拥有较小的跟踪误差便成了一个重要问题。股票指数跟踪技术主要需要解决两方面问题，一方面需要选取组合中的成分股，一方面需要确定成分股在组合中的权重。杨国梁等[2]将数学上处理高维变量选择问题的Lasso方法运用于股票投资组合构建中，取得了现有文献最好的跟踪效果。然而，Lasso方法本身确实存在一些缺陷。首先，若股票收益率存在严重共线性时，Lasso的选择效果会被削弱，其次是Lasso方法并不具有Oracle性质，而具备Oracle性质可以使得系数向量更接近真实值，且估计具有渐进相合性。ZOU[3]提出了Adaptive Lasso，该方法不但沿袭了Lasso方法的诸多优点，而且能有效减少模型参数估计的有偏性，具有Oracle性质。因此，将Adaptive Lasso方法运用于跟踪指数的股票选择中是一种很好的尝试。

1 指数跟踪方法

1.1 指数跟踪基本方法

现有的指数跟踪方法，按照原理不同，主要可以分完全复制法与不完全复制法两类。完全复制法是指购买标的指数中所有证券，并且各成分证券的权重完全复制标的指数的权重。其优点是能获得与标的指数相同的收益，拥有最小的跟踪误差，缺点是当指数构成变化时必须及时调整，从而产生非常高的交易成本。不完全复制法是指购买标的指数中的部分证券，使得收益率偏差在可控范围内，行业抽样配置法、市值占比法等都属于不完全复制法。由于不完全复制法可达到用较少证券获得较好跟踪效果的优势，因此国内外学者做了很多关于不完全复制法的研究。ROLL[4]基于Markowitz均值-方差模型，通过最小化指数跟踪误差与投资组合来确定成分证券的权重；ZORIN et al[5]将神经网络技术运用于指数跟踪方法也得到不错的结果，Corielli与Marcellino基于动态因子模型研究也解决了构建投资组合的问题。

1.2 Adaptive Lasso方法

1.2.1Adaptive Lasso简介

Adaptive Lasso的形式为：

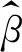
1.2.2Adaptive Lasso的算法实现

EFRON et al[6]提出的最小角回归算法(least angle regression，LARS)有效解决了此模型的求解问题；FAN et al[7]提出的循环坐标下降算法(cyclic coordinate descent，CCD)利用模型稀疏性的假定，算法简单运行快速；他还提出LQA方法对目标函数采用局部二次近似，然后采用Newton-Raphson迭代算法也可以十分便捷的得到计算结果。本文实证研究部分主要利用R软件的lqa package，其采用的就是LQA算法。LQA算法的数学思想描述如下：

记Adaptive Lasso的惩罚函数为pλ(|βj|)，pλ(|βj|)=λwj|βj|.

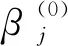
那么Adaptive Lasso惩罚函数的二阶Taylor近似展开函数为：

利用Newton-Raphson迭代算法，给可以出一个不含惩罚项的似然估计初始值β(0)，Adaptive Lasso就转换成了下面的形式的迭代求解问题：

当‖β(k)-β(k-1)‖<η时，算法终止，其中η可以取一个很小的正值。

2 Adaptive Lasso方法选择股票及实证分析

Y=Xβ+ε.

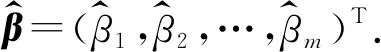
2.1 样本数据的选取

本文选择的指数跟踪对象为沪深300指数，选取了2015年8月3日—2017年10月28日，538个交易日的沪深300指数及各成分股的日收益率数据，其中2015年8月3日—2017年4月28日，共422个交易日为样本内区间，2017年5月5日—2017年10月28日，共116个交易日为样本外区间，用以检测跟踪效果。数据来源为网易财经。

2.2 Adaptive Lasso变量选择结果分析

基于Adaptive Lasso的基本思想，在R软件中运用LQA方法编程，便可同时实现股票的选择与权重的估计。图1-图3为100只股票，50只股票，30只股票的筛选过程。

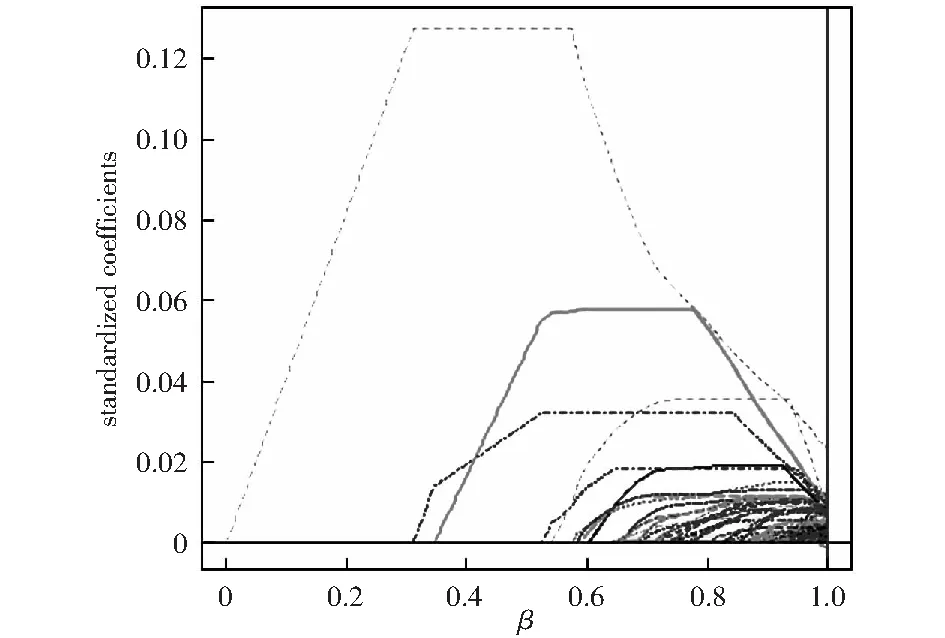
图1 100只股票的筛选过程

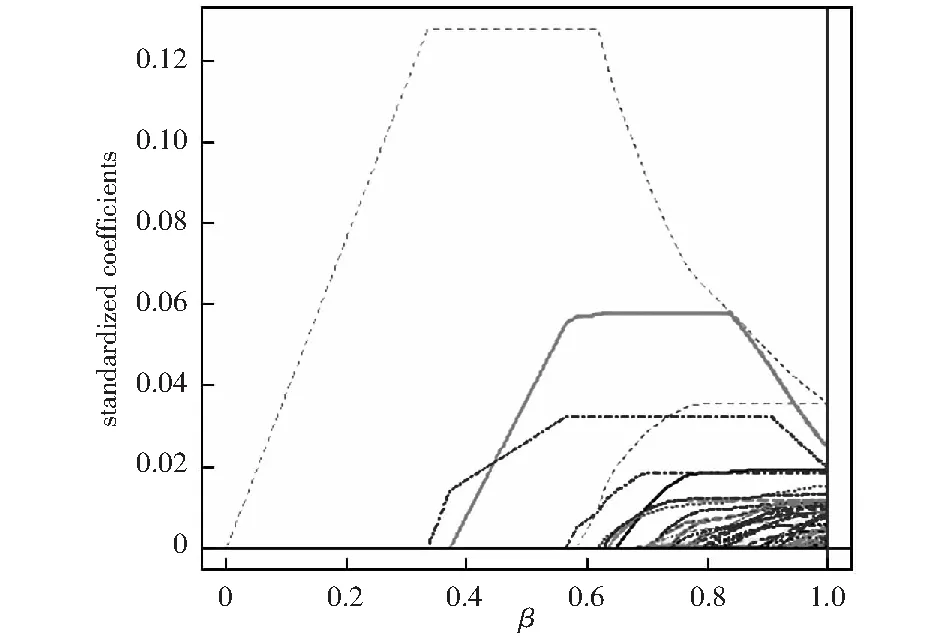
图2 50只股票的筛选过程

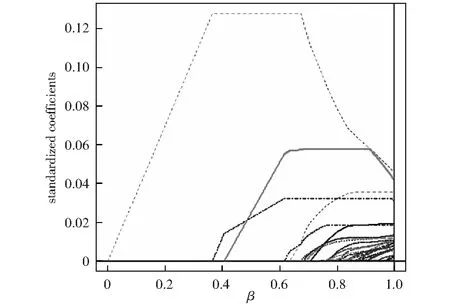
图3 30只股票的筛选过程

由图1-图3可以看出，Adaptive Lasso可以得到稀疏模型，随着参数的增大，一部分系数被压缩为0，即没有入选的股票所对应的系数β=0，入选的股票所对应的系数β>0，表1-表3为筛选出的股票名称及其权重系数。

2.3跟踪结果分析

为了对股票组合的跟踪效果进行评估，本文从相关系数、跟踪误差、最大正向误差和最大负向误差这4个方面验证分析，并比较了样本内区间与样本外区间的跟踪效果，如表4、表5所示。

表1 Adaptive Lasso选出的30只股票及权重系数

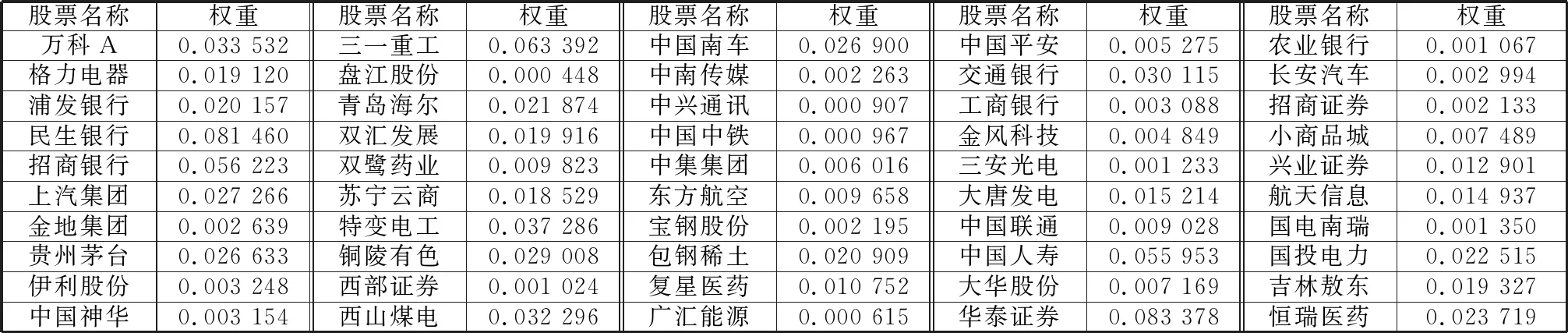
表2 Adaptive Lasso选出的50只股票及权重系数

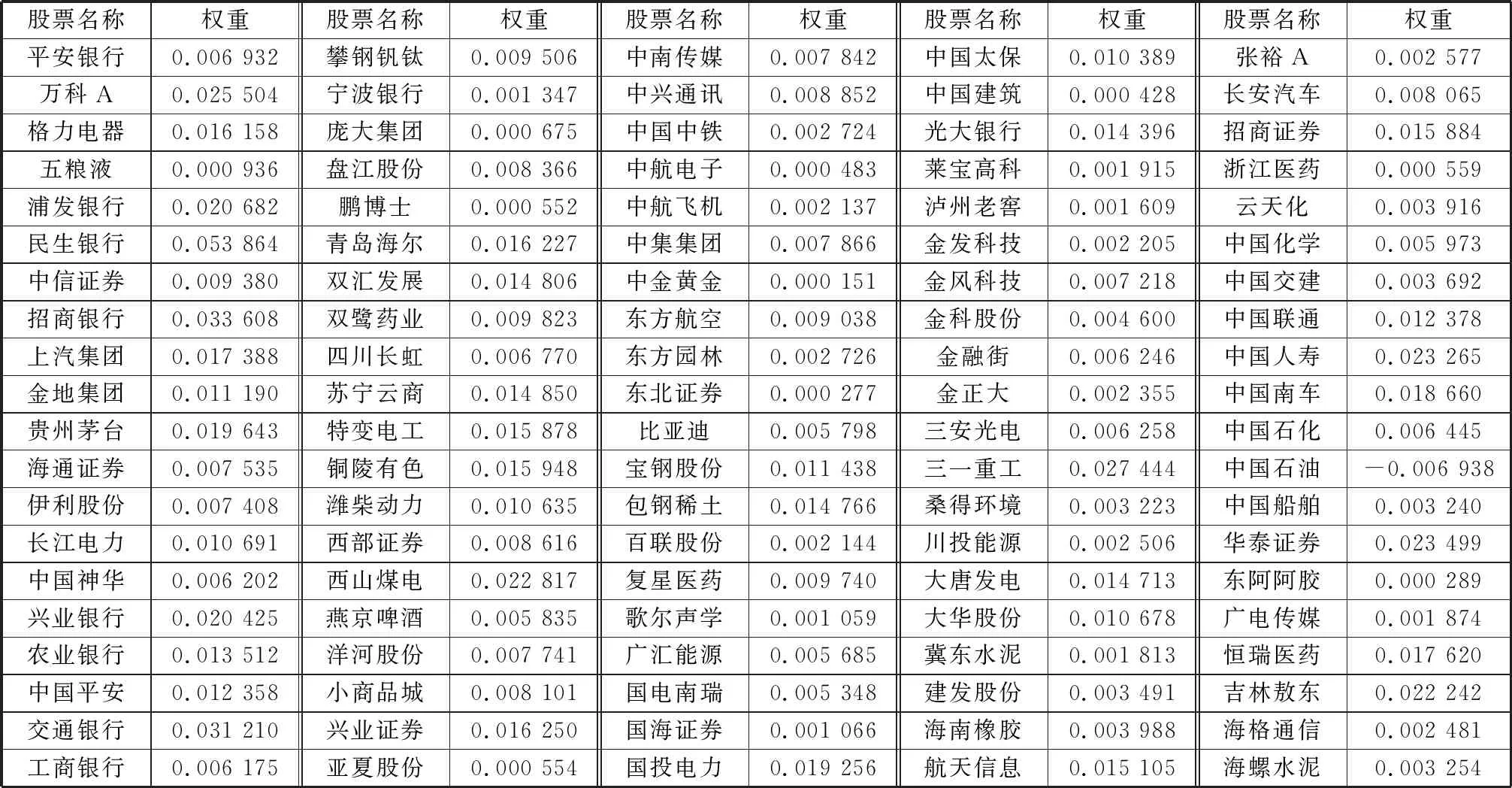
表3 Adptive Lasso选出的100只股票及权重系数

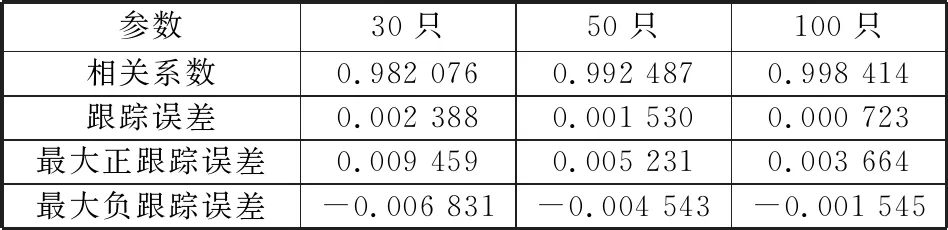
表4 样本内指数跟踪效果

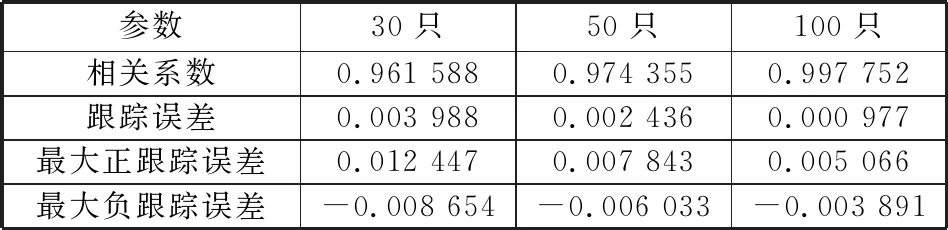
表5 样本外指数跟踪效果

结果显示，采用Adaptive Lasso方法构建股票组合，无论是30只、50只还是100只，都取得了非常好的跟踪效果。由样本内与样本外跟踪结果可看出：1) 相关系数均保持在0.96以上，说明成分股与沪深300指数相关程度很高，即指数跟踪的风险很小。2) 跟踪误差均可以控制在0.4%之内，指数拟合复制效果很好。3) 随着成分股的数量增多，相关系数增大，跟踪误差及最大正向误差和最大负向误差减小，说明成分股越多跟踪效果越好，这是显然的。4) 从整体看来，样本内指数跟踪效果要优于样本外指数跟踪效果，虽然样本外各指标数据都有一定的下降，但是幅度并不大，预测能力也是较强的。

3 结论

在瞬息万变的股票市场中，寻求一种性能良好的跟踪方法对目标指数进行有效跟踪，以此构建最佳股票组合，对于所有投资者而言具有十分重要的意义。本文将处理高维数据变量选择的Adaptive Lasso方法，运用于指数跟踪，同时完成了股票投资组合中成分股的选取与权重系数的估计问题。在实证分析部分中，利用Adaptive Lasso方法选择股票对沪深300指数进行跟踪，并从跟踪误差、相关系数等方面来衡量。通过比较可以看出，Adaptive Lasso方法可以达到比较理想的跟踪效果，具有一定的实用性，这也为金融市场的股票组合投资选择提供了一种新的方法。投资者进行股票投资最直接的动机是获得理想回报，故而投资决策的目标是收益的最大化。然而，收益和风险是正相关的，股市的波动一方面带来了投资收益，另一方面也带来了很高的投资风险，二者互相依存。我国的证券市场近年来一直处于高速发展过程中，但其系统性风险依然很大，投资者一直在寻求能够获得稳定收益的方法，尤其是当指数化基金、股指期货、ETF等衍生产品的不断推出，指数化投资被越来越多的人所关注。指数跟踪作为指数化投资的具体管理形式，可以有效的指导股指期现套利、指数投资产品的设计等。