核心素养导向下的高考数学命题创新探究
2020-02-04孔令润谈涛刘杰
孔令润?谈涛 刘杰
近日,中共中央、国务院印发了《深化新时代教育评价改革总体方案》,提出建立科学的、符合时代要求的教育评价制度和机制,为高考评价机制改革提供理论支撑和改革方向。高考命题在改革中不断探索创新,折射出国家对于新时代全面育人目标的要求,以《中国高考评价体系》为依托,以学科核心素养为导向,通过情境和情境活动两类载体,实现“四层”考查内容和“四翼”考查要求。拓展试题情境来源,巧设情境呈现方式和创新设问方式,已成为基于核心素养的高考命题改革和创新的基本原则。高考数学学科的情境包括三类:课程学习情境、探索创新情境和社会实践情境,三种问题情境在高考中发挥不同作用。以情境创新试题孕育创新意识,对于高中数学教学和备考具有现实指导意义。本文仅从四个方面对情境试题创新方向和策略进行探究。
一、利用时事热点问题为背景创设体育情境
高考强调学以致用。“在命题时应坚持理论联系实际的原则,使用贴近时代、贴近社会、贴近生活的素材,选取日常生活、工业生产、国家发展、社会进步中的实际问题”,情境类试题在近几年高考中出现频率呈现逐年加大趋势,它们从不同维度和视角将数学知识与社会热点紧密结合,考查学生的理性思维,数学应用和数学探索能力,体现素养导向和时代特征。下面是以体育素材为情境命制的一道创新题。
2020年9月13日,斯诺克2020/2021赛季大幕开启,斯诺克台球比赛以其特有的魅力而被广大群众所喜爱,比赛中击球规则可简化为:球桌上共有15个红球和6个彩球(黄、绿、咖啡、蓝、粉、黑),参赛选手需先击打红球,然后再击打彩球,之后红球和彩球依次间隔击打。若某次比赛中,参赛者开局连续打进10个球,则不同的击球顺序共有____种。
分析:计数原理是数学中的重要研究对象之一,排列、组合是解决计数问题的最基本、最重要的方法,它们为解决很多实际情境中的问题提供了思想和工具。实际生活中计算某种情形可能出现的种数,是最常见的设问方式,有时需要添加具有一定约束的条件,而斯诺克台球比赛中的击球顺序需满足一定的规则要求,可作为考查计数原理知识较为合理的载体。
本题的命题素材所隐含的数学知识(计数原理)和方法(排列数计算)均直接源自学生已有的学习储备,通过对击球规则的简化,提出了计算不同击球顺序的种数的问题。本题把数学核心知识的考查与体育紧密联系起来,体现“高考内容改革要贯彻五育并举的教育方针,完善覆盖德智体美劳全面发展要求的考试内容体系”的指导思想,贯彻高考命题“铸魂育人”的要求。试题情境新颖,问题设计难度适中,体现基础性,在考查学生的阅读理解能力的同时,激发他们对体育运动的兴趣。
二、用跨学科知识为背景创设学科交叉情境
在知识网络的交汇点设计试题,增强考核内容的基础性和综合性。在近几年的高考试题中可以发现有以化学、生物、物理、地理、医学等知识融合为情境载体,考查数学核心知识和关键能力的题目。下面是以高中物理知识为情境命制的一道创新题。
根据法拉第电磁感应定律,闭合电路中瞬时感应电动势false的大小,跟穿过这一电路的磁感应强度false与该闭合电路的面积false的乘积的瞬时变化率成正比,即false,已知false,false,false,则当false时,_________ false。
分析:求物理量的瞬时变化率需要用到导数这一工具,而物理学科中的法拉第电磁感应定律涉及磁通量的瞬时变化率的问题,磁通量与磁感应强度和闭合电路面积有关,且高中物理对这一知识的要求一般是磁感应强度不变或者闭合电路面积不变,学生在学习过程中可能会对这两者都发生变化时的问题感到好奇,但又不知该如何解决。
本题选取物理学科中的法拉第电磁感應定律为命题情境,与高中数学中的函数求导乘法法则问题建立关联,属于对基本知识和运算能力的考查。与物理中求瞬时感应电动势不同的是,试题中的磁感应强度false与闭合电路的面积false均随着时间false的变化而变化。试题设计巧妙,在考查数学知识的同时,也有助于加深对物理学科中法拉第电磁感应定律的理解,凸显了数学的工具性特征,展现数学的应用价值,符合跨学科命题的特点。
三、用传统文化及数学史等为背景创设文化情境
数学文化是对数学知识、技能、能力和素养的高度概括,无论是中国文化的源远流长,还是世界历史的百家争鸣,数学都在其中留下了不可磨灭的宝贵成就。数学文化是一种理性的艺术,利用传统文化及数学史等为背景创设文化情境类试题,可以让学生感受先贤天马行空的想象和精益求精的科研精神,从而勇于创新,不断求索。纵观近几年的高考数学命题,数学文化类试题已经从开始引导到逐步渗透,逐渐浸润到数学的每个模块和专题中,这也是顺应新课改和新高考对育人方式变革要求的又一举措。
命制符合新课改导向的数学文化情境试题,可以采用先选取素材,再确定考查的知识点,或者先确定考查知识点再反方向寻找素材的方法,下面以先选取素材再确定考查知识点的方法为例说明。
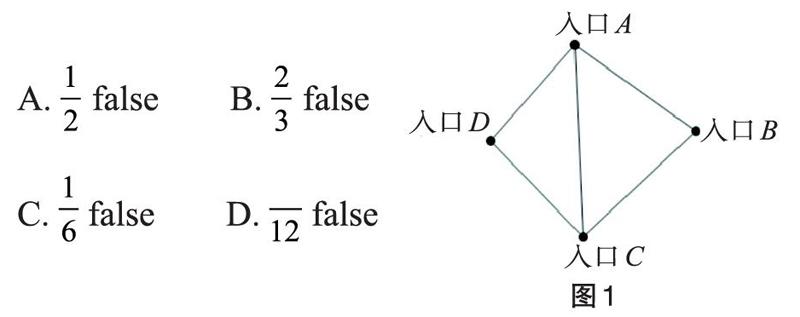
18世纪初普鲁士的哥尼斯堡有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来。当地流传着许多与七座桥有关的传说,其中一个是这样的:能否不重复、不遗漏地一次走完七座桥。1736年,29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,在解答问题的同时,开创了数学的一个新的分支—图论与几何拓扑。同学A和B在如图1所示的花园中模拟这个问题,他们同时从四个入口中任意两个不同的入口出发,则他们都可以不重复、不遗漏地游览完整个花园的五条路的概率是___________。
A.falseB.false
C.falseD.false
分析:本题的材料背景来源于《人教A版 选修3-1 数学史选讲》,故事流传性很广。被选入小学、初中、高中课本,很好地体现了数学的连续性和延展性。材料中欧拉从这个问题开创出了数学新的分支—图论与几何拓扑,是对现有问题经过思考后的总结升华,整个过程引导、启发学生用发展的、关联的眼光看问题。选定素材后,即可确定材料想要考查的知识点,材料中“怎样才能不重复、不遗漏地一次走完七座桥”暗含了两个核心关键“能不能完成”以及“如何完成”,这其中涉及了“选择”和“事件”,与概率知识点有很高的关联性,故可以创设如下命题原型。
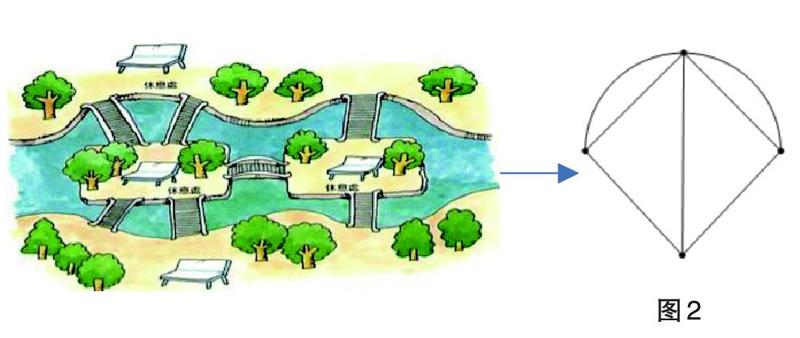
从图2四个点出发可以不重复、不遗漏地走完所有线路的概率是多少?
本题在情境问题设计方面,受学生是否看过欧拉解决这个问题的方法影响,难度会有较大变动,不符合公平性原则,故设计的问题可以考虑减弱学生在判断是否能完成上的难度,增加对概率知识的考查,即可得到上述例题。当然,也可以通过改变设问方式适当增加难度。
四、用贴近生活的熟悉背景创设实际应用情境
给一些简单的问题赋予应用的情境是试题改编的一种方式,合适的问题情境可以赋予枯燥的数学知识以鲜活的生命力。在赋予一定的应用情境的同时,还需要在数据、数量关系等方面进行再加工,使之贴近生活实际。
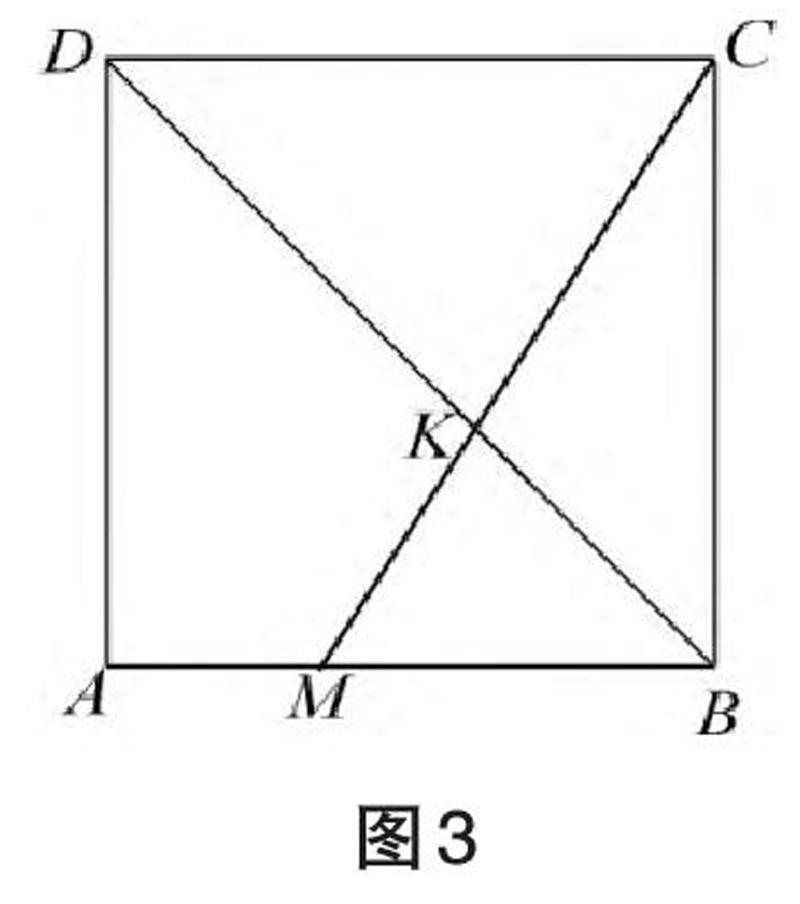
原題:如图3,K是边长为1的正方形ABCD的对角线BD上一点,连接CK,并延长交边AB于点M,求ΔCKD与ΔBKM的面积和的最小值及此时的DK长。
加载情境后的改编题:如图3,某园林规划部公司计划在一块边长为2百米的正方形区域ABCD内设计两块绿化区域和两块休闲区域,具体设计的方案为:在对角线BD上取一点K(不含端点),连接CK并延长交线段AB于点M,ΔCKD与ΔBKM为绿化区,其余区域均为休闲区,已知绿化区每平方百米造价为50万元,休闲区每平方百米造价为25万元,设DK长为x百米,绿化区和休闲区的总造价为false万元。
(1)求函数false的解析式,并指出其定义域;
(2)当DK长为多少时,总造价最少?最少为多少?
分析:原题是一个纯数学情境的几何问题,赋予应用情境后改编变成有一定阅读量、数量关系也较原题复杂的应用题,要求学生能够从实际应用情境中抽象与提取数学问题,建构与解决相应函数模型,属于较复杂的生活实践情境,对学生的数学阅读与理解能力、信息识别与提取能力有较高要求。改编后的试题在综合性和应用性层次上考查学生的数学建模、数学运算等素养以及对新问题的探究能力,体现了数学的应用价值和在解决实际问题中的作用。
总之,试题情境的创设,既为提高试题质量提供技术保障,也为实现价值引领、素养导向、能力为重、知识为基的命题理念提供方法保障。在创设试题情境时,多结合社会现实,反映数学应用的广阔领域,体现数学文化和数学应用的领域,回归学生发展,回归数学本质,回归教育规律,回归实际背景。情境材料所隐含的知识与方法,必须与试题的考查内容、考查要求相一致,情境的设置和对考生解题思路的预设应当符合中学生实际的认知水平,使考生能够应用所学知识对题干内容进行深层挖掘和分析,其作答应该能够体现分析和解决问题的思维过程,使数学的重点知识、技能方法成为考生分析、解答问题的有效工具,培养考生灵活运用所学知识解决各类问题的良好思维习惯,为其今后的成长和发展提供智力支持。研究情境类试题的创新策略,对提高数学教师创新型试题的命题意识和培养学生数学创新能力是有益的。
(作者单位:科大讯飞)
责任编辑:李莎
lis@zgjszz.cn
