立足“HPM”,彰显数学文化
2020-02-04周作雄
周作雄
【摘要】“HPM”以其丰富的数学概念、思想、方法,深邃的人文底蕴,成为课程资源开发的重要载体。立足“HPM”M,对数系教学做出优化和改进,其目的在于激发学生学习兴趣、发展其数学核心素养,建构其正确的数学观的同时提升质量、彰显数学文化。
【关键词】HPM;数系教学;数学核心素养;数学文化
在《教育部关于全面深化课程改革落实立德树人根本任务的意见》中,对核心素养进行了明确界定,核心素养系学生应具备的适应终身发展和社会发展需要的必备品格和关键能力。在教育部最新颁发的课程标准中,就把如何发展学生的核心素养作为贯穿课程标准的主线,高中新课程实施中要将它将全面实施并展开。在《高中数学课程标准》中,提出了6个核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析,教师如何在自身课程实施中实现发展学生数学核心素养,并以此为目标,成为当下数学教学研究一个热点问题。
学科核心素养的提出,其目的在于将以知识为中心教学目标向能力为核心教学目标转型,所以我们的教学不应当只是一种单纯的知识教学,还应该是一种以发展学生能力为主导的教学,这其中,数学文化就起着十分重要的作用。在这个教育背景下,我们的教学就应当将知识教学与文化教学进行紧密的结合。在我们的数学教学中,要培养学生的数学核心素养,必须考虑加入数学的相关文化,因为它扮演着一个不可或缺的角色。其实,在2003年颁布的《普通高中数学课程标准》中,已经明确了数学文化具有的价值,“数学课程应当适当的反映数学的历史、应用和发展趋势,数学对推动社会发展的作用,数学的社会需求,社会发展对数学的推动作用,数学的思想体系,数学的美学价值,数学家的创新精神。数学课程应帮助学生了解数学在人类文明发展中的作用,逐步形成正确的数学观。”
一、“HPM”:教学融入数学文化的载体
“HPM”是History and Pedagogy of Mathematics 缩写,中译为数学史与数学教育。“HPM”有两方面的含义:其一是指在国际数学教育会议上专门讨论数学史和数学教育融合的研究团队;其二是指这个团队的研究对象“数学史如何与数学教育融合在一起,共同促进学生的发展。”“HPM”的功能有宏观与微观之分。宏观上:①贯通数学的历史,把握数学发展的脉络,加深对数学概念、方法、思想的理解;②整合数学学科,理清数学学科的关系,体会数学创造过程;③把数学从课内导向课外,形成对文化的历史认同感;④传承数学史的文化,给予数学以人文的一面。微观上:①增强学生的学习动机;②帮助学生形成正确的数学观;③有助于学生保持对数学的兴趣。其中汪晓勤教授将其总结为:“HPM”不仅可以激发学生的学习兴趣,培养学生的数学精神,启发学生的人格成长,预见学生的认知发展,指导并丰富教师的课堂教学,促进学生对数学的理解和对数学价值的认识,构建数学与人文之间的桥梁。
作为数学老师,我们应该如何将数学文化元素融入教学呢?喻平教授给出了他的建議,他认为数学老师首先在教学设计时就要思考这样三个问题:①为什么我们要研究这个数学知识?②我们应该如何去研究这个数学知识?③这个数学知识它有什么样的意义与价值?思考完这三个问题后,数学文化的味道马上就出来了。第一,为什么我们要研究这个数学知识?这个问题必然与我们的数学史相关联,我们就会去数学史中去寻求我们的答案。寻找这个问题的起源,同时从社会需求以及数学学科发展需求两个方面去思考,从而揭示陈香的数学文化。第二,我们应该如何去研究这个数学知识?这与我们的数学思想方法相关,数学思想方法是我们数学文化中的精髓,通过揭示其中的思想方法,来宣扬科学家的理性精神、求实态度,由此彰显深邃的数学文化。第三,这个数学知识它有什么样的意义与价值?我们老师就会去思考这个数学知识有什么社会价值、文化价值以及科学价值、以及有什么美学的价值?或者是有什么思维训练的价值,等等,由此便可以散发浓郁的数学文化来了。显然,思考前面两个问题就与HPM产生必然联系,因此,“HPM”中教学融入数学文化的一个重要载体。
二、数系发展:写实记录数学文化的迹印
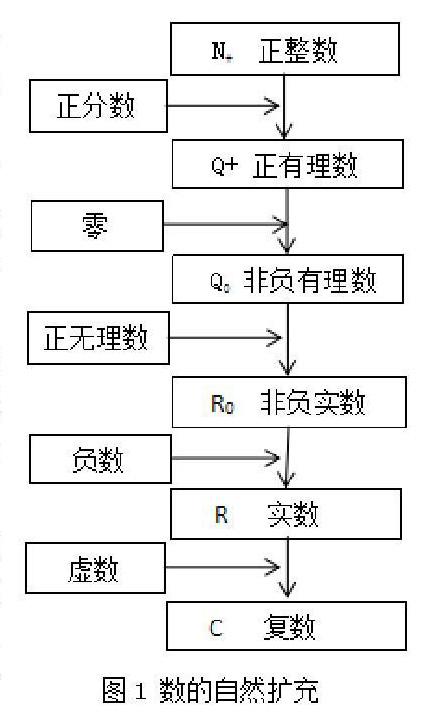
在中学数学内容中,数的扩充如图1所示。这是一个简单的图示,其实是经历了一个漫长的历史过程形成的,里面充满了许多故事,留下了浓墨重彩的数学文化迹印。
负数产生的历史。我国古代著名的数学专著《九章算术》中,最早提出了正负数加减法的法则,三国时期的学者刘徽(公元225-公元295)对《九章算术》作了详细的注解,并最先给出了正负数的定义。东汉末年时期的刘烘(公元206年)、宋代的杨辉(1261年)也著书提到了正负数的加减法则,元代时期的朱世杰)不但给出了正负数同号异号的加减法则,同时还给出了正负数的乘除法则,所以它在前人的基础上又前进了一步。但是,负数在国外被认可和被接受,比我国要晚很多。在印度,数学家婆罗摩笈(Brahmagupta,公元前598-公元前668)多于公元628年才认识负数可以是二次方程的根,欧洲是在14世纪,当时在数学方面最有成就的法国数学家丘凯(ChuQuet)还把负数当成是荒谬的数,不给予理会它。一直到十七世纪,荷兰有出现了一个叫日拉尔的数学家,他最先开始认识并使用负数来解决几何问题。
无理数的故事。一群毕达哥拉斯的门徒地海上泛舟,其中一位学者看着辽阔的海面兴奋地说:“毕达哥拉斯先生的理论是多么的正确啊!你们看这大海的波浪一层又一层,波峰浪谷,就好像偶数和奇数相间一样,所以我们的世界就是数字的秩序。”“是的,是的。”这时一个正在摇桨的大个子插进来说:“就说这小船和大海吧。用小船去丈量这海水,肯定会得出一个精确的数。一切事物之间都是可以用数字互相表示的。”
这时船尾的一个名叫希帕索斯的学者突然提问了,他说:“我看不一定,要是量到最后,不是整数呢?”有人说:“那就是小数。”希帕索斯接着再问:“要是这个小数,它除不尽,也不能循环,怎么办?”有人马上回答“这是不可能的事,世界上的所有的东西,都应该可以用数字,把它直接准确地表达出来的。”这时,希帕索斯瞥了一眼,然后说道:“世界上一切事物不一定都可以用我们现在知道的数来表示吧,就拿直角三角形来说,假如它是一个等腰直角三角形,我们就无法用一个已知数来表示斜边。”这时候,一个划船男人一听这话就不开心了,并且大叫呵斥道:“不可能,毕达哥拉斯的话放置四海皆是正确的。”于是,希帕索斯伸出自己的双手,用手的两个虎口比作一个等腰直角三角形,然后说道:“如果大拇指直边和食指直边都是3,那么等腰直角三角形的斜边是多少?我已经算过很多遍,所有的已知等腰直角三角形,它的斜边都不能用一个整数表示出来。”他的这话像一声晴天霹雳,全船的全员听到后都愤怒了,然后大声地骂道:“你敢不认可毕达哥拉斯先生的理论,想破坏我们的信仰!敢不相信我们的世界是由数字组成。”希帕索斯这个时候表现得十分的冷静,并说道:“这是我的新发现,我应该被奖赏,而不是在这里被你们侮辱。你们可以去证实,看我说的是否正确?”然而当时船上所有的人,他们根本听不进去他的解释,对他大声吼道:“你就是个叛逆!我们学院没有你这样的学生。”这时开始有人起哄,说道:“打死他!批死他!”一个壮汉冲上来,就是一拳。希帕索斯口吐鲜血说道:“你们无视科学,你们这群土匪、强盗、莽夫!”这时,人群中又有人喊道:“我们要捍卫我们学派的信仰,它永远对的。”然后又有一个人高马大的人也冲过来,奋力将他抱起,说道:“痴人说梦,去海里好好地清醒一下吧!”说着就把我们主人公扔进了海里。汹涌的海水很快将他给淹没了,然后他就再也没有回来了。一位这么有思想、有才华的数学家就这样被一群无知的信徒给杀害了。
在这次事过去很多年以后,不少毕达哥拉斯学派的成员也慢慢发现,不但等腰直角三角形的斜边,而且我们的圆,还有那个数字3.14159265358979……更是永远也无法用整数来精确表示的。慢慢地,信徒们开始后悔了,后悔杀死希帕索斯的鲁莽行动。最后人们也渐渐明白,除了我们所认识的有理数之外,还有一些无限的不循环的小数,它确实是一种的数,是新发现的一类数,它的名字就叫做“无理数”。
由无理数引发的数学史上第一次数学危机一直延续到19世纪。1872年,德国数学家戴德金(Julius William Richard deakin,1831-1916)从连续性的范围出发,用有理数的“分割”来定义我们的无理数,并把无理数和有理数扩充到了实数范围内,有了实数理论的科学基础,无理数由此也结束了,它“无理”的时代,它的结束,也标志着数学史上持续2000多年的第一次数学危机得到解决。
虚数的故事。虚数诞生于欧洲文艺复兴时期的三次方程求解。我们知道,二次方程可有简单变换,得到通解公式,当判别式为负值时无解。到了14世纪,数学家开始探索三次方程的求解,这个过程耗费了几代数学家的心血,直到16世纪的意大利数学家西皮奥内·德尔·费罗(Scipione del Ferro,1465-1526年),首次得到了标准形式三次方程的通解,但费罗并未把他的解法公布出来,而是带进了坟墓。另一位数学家塔塔里亚(Nicolo Tartaglia,1499-1557年),在1535年得到了同样的通解公式,和他的前辈费罗一样,丰塔纳也秘密保守他的发现。另外一位数学家卡尔达诺(1501-1576年)听说了塔塔里亚知道三次方程的求解,于是卡尔达诺就去请求告诉他关于三次方程的相关解法,塔塔里亚在卡尔达诺多次的请求下,告诉了他三次方程的求解公式,但并未传授三次方程公式的推倒过程。
方程的求根公式为:
卡尔达诺守着他的承诺,保守三次方程的求解秘密,直到他听说了费罗的故事,才得知原来塔塔里亚,并非第一位得到三次方解的人,这时卡尔达诺认为他对塔塔里亚的承诺已经没有意义。1545年,卡尔达诺出版了他的数学名作《大衍术》,在书中他给出了塔塔里亚的求解公式,并发表了三次方程的解法,他在书中做了一个重要的突破,把这一解法推广到了三次方程的一般解。
然后虚数i,就隐藏在这个看似复杂的公式当中,这个公式蕴涵了一个新数学领域的诞生,她需要一位超级天才去发现。从卡尔达诺的《大衍术》开始,200多年时间中,人们不断遇到负数的开方问题,但采用不以敢承认和回避的态度,于是虚数一直披着神秘莫测的外衣,到了1797年,威赛尔给出了虚数的图像表示,后来高斯在平面直角系中就建立了点与复数之间的一一对应关系,并提出用数偶(a,b)来表示a+bi,这样才确立了复数的合理地位。
这些故事展现了数学真理发现的艰辛历程,反映了人类文明推进的艰难,同时,更加彰显了科学家不屈不挠探求真理的执着和为科学献身的精神。数系的发展史蕴含丰富的文化元素、厚重的文化积淀,如果不挖掘这种以内隐形式潜藏于知识深层的课程资源于教学之中,无疑是一种莫大的浪费、资源的流失。
三、文化融入:数系教学的不同形式
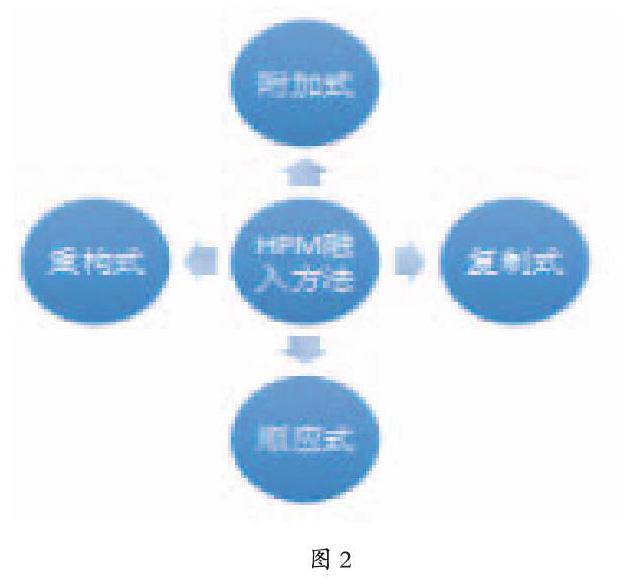
HPM融入教学的方法有许多,其中就包括:介绍历史上数学家的故事;运用数学史引入新概念;讲授“数学史”课;利用相关历史史料的教材设计来布置课堂练习和课后作业;举办数学历史主题的班会;借鉴历史发展,设计话题式的教学;以及探索过去数学史上的数学错誤、另类观点来帮助今天的学习者理解并解决他们的困难等等。汪晓勤教授把“HPM”融入到课堂教学的方式归纳为四种方式(如图2所示):
①附加式:讲解数学数学家轶事与生平;②复制式:将数学家的解题方法直接呈现;③顺应式:根据历史史实,合理改编数学素材;④重构式:重构知识发生发展的过程。
(1)以顺应式的方式将“HPM”融入负数的教学设计
1.情景设计
师:同学们能用以前学过的知识来解决下列问题吗?
(1)小梦买练习册一共花了4.5元钱,现在她有了5元钱,她还剩多少元?
(2)若小梦手上只有4元钱,她能买到想要的练习册吗?为什么?
生:用小梦手中的钱减去本子的价格得:5-4.5=0.5。
师:那么第二问该怎么解答?(引导学生第二个问题也用手中的钱数减去本子的价格)
生:老师,我只会列出式子,不能得出答案:4-4.5=?
师:其他同学是不是也是这样的答案,不够减?
(设计意图:从具体生活情境引入,引导学生逐步抽象出数学问题,并通过构造无法计算,不能减的认知冲突,激发起学生的求知欲,从而培养学生的数学抽象、逻辑推理、数学计算等素养)
2.数学相关历史介绍
师:大家现在还不怎么会做,其实是很正常的,老师可以理解,因为在我们历史上,有许多的数学家也都曾经被这个所问题困扰呢!如代数学鼻祖丢番图,他在其《算术》中称4x+20=4方程是没有意义的。同样,斐波拉契在《花朵》中称方程x+36=33是没有根据的。如何解决困惑呢?我国古代杰出的数学家刘徽给出了区分的方法。他用正算赤,(下转第23版) (上接第22版)负算黑来表示。所以我们也可以借用前人的方法,用红黑颜色的数来加以区别。
我们不妨以较大的数减去较小的数的结果来表示运算结果,只是为了区分,我们用黑色来表示,即把这个结果用黑色的数来表示区别。因此,4-4.5=0.5。
师:那么,以下的式子结果等于什么?0-2=?0-4=?0-6=?
生:我是模仿了上面的方法,得2,4,6。
师:我们知道,加法和减法互为逆运算,那么下面运算结果是多少?2+2=?4+4=?5+5=?
生:很快得出结果:0。
师:那么,以下式子结果等于什么呢?0-2=?0-4=?0-5=?
生:我的答案是:2,4,5[师]完全正确。
师:我们把这里的这种特殊的黑数称为负数。而我们原来的数除了0以外的数,称为正数。负数的表示是在相应的正数前面加符号“-”,例如上面的2,4,6,我们可以表示为:-2,-4,-6。
(设计意图:这种引入是建立在小学生的认知基础之上的,更能引起他们的兴趣,培养他们的数学思维,同时有利于打造浓浓的数学人文课堂,对于培养小学生的创新精神和数学核心素养起着举足轻重的作用)
3.课后引入
老师可以将有关负数的发展历史史料提供给学生,让学生对于负数有更深的了解。
(设计意图:将有关负数的发展历史作为史料提供给学生,进一步破除他们对负数的困惑和恐惧感,以及指导学生探究学习,彰显数学的文化魅力,使数学学习成为学生们获得知识、形成方法、感悟价值、提升素养的生命历程)
(二)以附加式的方式将HPM融入无理数的教学设计
1.视频引入
让学生观看《科学世界》中视频,通过视频中,人类如何寻找地球外的生命,以及发射“勾股定理图”来作为与外星文化取得联系的信号,来提出本节课需要探究的问题:为什么勾股定理图可以作为与“外星人”联系的信号?
(本环节设计意图:巧妙地视频引入,激发学生的对勾股定理的兴趣,以及思考勾股定理有何魅力,可作为外星文明沟通的桥梁)
2.插入故事
师:同学们,现在老师给大家介绍一下毕达哥拉斯的故事。(插入前面“无理数的故事”)
(本环节设计意图:巧妙得借助无理数的故事,将学生带入了无理数的世界。通过数学史再现,让学生感受到数学知识发生的动人历程,以及体会数学家为数学真理而奋斗甚至献身的崇高精神)
3.动手实践
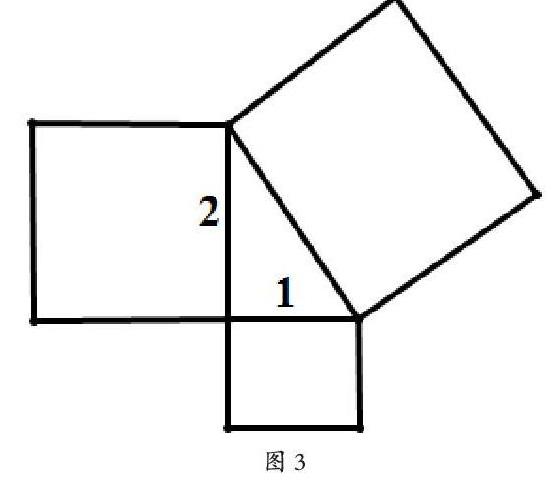
师:请学生拿出课前准备好的纸和剪刀,动手剪一剪,拼一拼,设法得到一个经典的毕达哥拉斯的勾股图(如图3所示)。思考这样一个问题:在直角三角形中,若两条直角边长为a,b,斜边为c,则有a2+b2=c2。若a=1,b=2,则c2=12+22,即c2=5,则c是有理数吗?
师:有理数包括什么?
生:整数和分数。
师:c2=5是整数?是分数?
生:22=4,32=9,所以c应该是在2和3之间,故c不是整数。
生:分数不可能,两个相同的分数相乘都为分数,所以c不可能是分数。
师:回答得很好。我们把上述c2=5中,c既不是整数,又不是分数的数称之为无理数。
(本环节设计意图:培养学生动手实践能力的同时,促进其对毕达哥拉斯学派成就有深入的了解,从而给学生普及更多的人文味的数学)
4.课后引入
选做题:以小组为单位的形式,让他们去查阅以及收集无理数相关的数学史料,作为数学知识分享会或者班级数学角的宣传资料。
(设计意图:让学生在查阅无理数的数学史料过程中,对数学的发展产生一定的熟悉和相应的认知,从而扩大他们在此方面的了解、增加他们的知识面,让初中阶段的学生了解到数学学科中的每一个知识都不是简单地产生的,从而激发初中阶段的学生对数学未来领域的好奇心。)
(三)以复制式的方式将“HPM”融入复数教学设计
1.问题引入
师:意大利数学家卡尔达诺曾经困惑于这样一个问题:求同学们是否可以帮其求解?
生:
生:因为,所以,又因为,所以此方程无解。
师:两位同学的回答都很棒,但都不是正确答案。那么此方程的答案究竟是怎样呢?老师先保持一下它的神秘感。
(设计意图:通过引入意大利数学家卡尔达诺在对“求的问题,在实数域上无解的过程来引起学生的认知冲突,同时让学生初步感知虚数的存在。)
师:接下来,我们再来看一下德国数学家莱布尼茨所困惑的问题:求解方程:,还是有请同学们帮他求解一下。
生:,再将其代入得.令,所以此方程无解。
师:回答的非常不错,值得表扬。但是很遗憾,没有回答正确。此方程真的无解吗?
(设计意图:通过再引入莱布尼茨对的解题困惑,再次激起学生认知冲突。同时让学生们去感受虚数和实数之间是存在某种联系的,从而为学生的学习创造动机)
2.数学相关历史引入
师:我们来看看虚数引入的历史,插入前面“虚数故事”。
(设计意图:复制式教学可以促进学生的理解,在数学与历史之间架设一座桥梁,使得学生可以发展其思维和想象,培养其文化素养。其次,让学生体会历史相似性,了解前人对虚数的发现过程并不是一帆风顺的,并告诫他们在以后的学习过程中不要轻言放弃)
3.课后引入
选做题:以四人一组的形式,让他们去查阅复数相关的发展史料,下节课围绕学生收集内容进行进一步的展开讨论以及延伸,最后可收集优秀学生的资料,指导其发表相关虚数论文。
(设计意图:高中阶段的学生团结、协助能力已经具备,让他们讨论、整理以及发表数学史小论文,不仅可以完善其对数系认识的整体框架,还可以添补其数学文化历程。这一做法有效的激发起了学生对于数学文化的探究的热情以及为数学发展奋斗终身的志向)
数系的发展史蕴含丰富的文化元素、厚重的文化积淀,充分挖掘其价值,恰如其分地切入,不仅可以契合学生学习认知、激发求知欲、增强数学文化的提升以及数学观的建立,而且对于彰显中国数学历史文化、培养民族自豪感、以及发展数学核心素养都有同工之妙。
参考文献:
[1]喻平.发展学生学科核心素养的教学目标与策略[J].课程·教材·教法2017,37(01):48-53+68.
[2]中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社, 2016: 2-5,34-35.
[3]汪晓勤,欧阳跃.HPM的历史渊源[J].数学教育学报,2003(03):24-27.
[4]喻平. 发展学生的关键能力:小学数学教学的根本任务[J]. 教育视界, 2018(04):4-7.
[5]陈天宇.HPM视角下的高中数学教学优化设计例析[J].数学教育学报, 2017(21):3-5.
[6]Fauvel J, Maanen J V. History in Mathematics Education[M]. Springer Netherlands, 2000(6).
[7]汪曉勤.HPM的若干研究与展望[J].中学数学月刊, 2012(02):1-5.
