煤储层渗透率拟稳定评价方法

刘 佳， 李 娜， 柳迎红， 冯汝勇， 王存武

(中海油研究总院有限责任公司， 北京 100028)

渗透率是煤层的固有属性，煤层渗透率的大小对煤层气井产量、钻井方式、增产措施等均有直接的影响[1-3]，煤层渗透率是煤层气开发过程中至关重要的一个影响因素。关于煤层渗透率的研究主要集中在煤岩孔隙及裂隙结构[4-9]、煤层渗透率的影响因素[10-14]以及煤层渗透率大小研究等。

目前定量评价煤层渗透率的主要手段有不稳定试井、岩心实验、测井解释等。由于煤层渗透率极低，通过压力恢复测试所得双对数曲线特征不完整，一般只有井储阶段及过渡段，解释结果偏小且可靠性差，试井解释结果一般在0.01 mD及以下[15-16]，与数值模拟解释渗透率相差超过100倍；且在实际的煤层气生产现场，有时没有上述资料或者参数点较少，无法清楚认识区块渗透率分布规律。而室内实验方法目前尚未得到广泛应用，主要由于煤岩获取难度大且煤岩易破碎[17-18]，采用完整煤样进行渗透率测量难度较大，且在钻取煤岩过程中，容易导致煤岩产生裂缝，渗透率实验结果可靠性差。而大部分室内实验通常使用煤岩颗粒压实后进行测量[19-21]，通过对比原始煤样与压实制造煤样的孔隙度、渗透率等参数可知，将煤岩颗粒压实后测量得到的结果与实际差别较大[22]。基于测井资料解释储层渗透率在常规油气藏中已非常成熟，但由于煤储层资源较为特殊，煤层气的电性过于复杂，孔隙和裂缝也比较多，以往所采用的评价方法无法在煤层气中有效运用，很难获取精确的数据信息[23-24]。

综上所述，目前大多数煤层气区块对储层渗透率无法准确认识，在进行产能预测、低产低效井分析时无合理依据。为了对煤层渗透率进行计算，基于煤层气井生产数据反算煤层渗透率逐渐受到研究人员认可与重视[25-26]。目前已有多篇文献研究了煤层气井产能方程以及渗透率求解模型，但大部分研究均基于稳定渗流模型。煤层气储层属于衰竭开发，无能量供给，与稳定渗流差异较大。

为了明确煤层渗透率大小及分布规律，现从煤层气井单相排水阶段时的压降规律出发，建立不稳定渗流模型下渗透率计算方法。旨在为煤储层物性和煤层气开发方面提供较为详尽的理论依据。

1 拟稳定评价方法建立

1.1 拟稳定评价方法原理分析

对于煤层气储层，储集层外面无能量补充，且多口井排采时，根据叠加原理，井距位置处可等效为一条不渗透的封闭边界。且由于煤层气属于吸附气，只有当压力低于临界解吸压力后，煤层气开始解吸从而被采出。故在排采初期，为了使煤层气解吸，煤层气井井底流压应连续下降，产水量稳定。图1所示为煤层气储层内各点压降曲线的变化情况。

图1 封闭边界下煤层气井生产时压力降落变化曲线Fig.1 The pressure drop curve of coal-bed gas wells produced in closed boundary

对煤层气井压降漏斗进行分析可知，当压力传到边界后，由于无外来能量供给，边界处的压力就要不断下降，在开始时边界上各点压力下降幅度比井壁处压力下降幅度要小，但随着时间的增加，从井壁到边界各点压力下降幅度将逐渐趋于一致，这种状态称为“拟稳定状态”。拟稳定渗流是不稳定渗流的一种特殊状态，根据拟稳定渗流的定义，可以求得煤层渗透率的解析解。

由于地层是封闭的，根据物质平衡原理可知，煤层气井产水量为

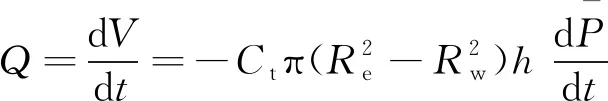
(1)

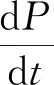
(2)

式(2)中：Pwf为井底流压，MPa；Pe(t)为地层压力，MPa；μ为地层水黏度，mPa·s；K为渗透率，mD。

(3)

式(3)中：P为地层内任意一点的压力，MPa；A为压降区面积，m2；r为压降区半径，m。

可得到平均地层压力关系式为

(4)

对于人工压裂井来讲，可以用等效井半径Rwe代替Rw。

其中有

Rwe=2xfe-3.5

(5)

式(5)中：xf为裂缝半长，m。

当煤层气井累产水量为W时，即可根据物质平衡方法得到关系式为

(6)

式(6)中：Pi为原始地层压力，MPa。

(7)

得到拟稳定生产时，煤层渗透率计算公式为

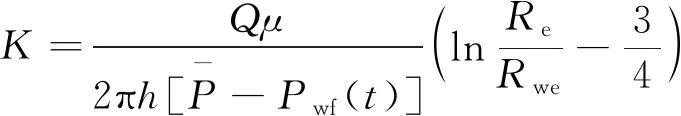
(8)

通过式(8)可对煤层渗透率进行计算，其中平均地层压力可用式(7)求得。该方法称为煤层渗透率拟稳定评价法。使用该方法时，应采用煤层气井拟稳定渗流段的生产数据进行计算，根据拟稳定流判别条件，当t为30 d时，能够满足从井壁到边界各点压降幅度逐渐趋于一致。即排采30 d后能达到拟稳定渗流，可选取排采30 d后至见气前(纯产水阶段)的数据进行计算。

具体步骤如下：首先，整理数据，其中包括日产水、累产水、井底流压、井距、煤层厚度等数据；其次，基于式(7)计算不同时间下的地层平均压力；最后，采用排采30 d以后的纯产水生产数据，基于式(8)计算煤层渗透率。

1.2 拟稳定评价方法优势分析

该方法基于封闭油气藏拟稳定渗流模型进行计算，与前人计算方法相比，具有如下优势。

1.2.1 更符合实际渗流

目前文献中往往采用稳定渗流模型的方法计算煤层气储层渗透率，如文献[19]，基于稳定渗流时的产水量公式，推导得到渗透率计算模型。但稳定渗流发生的条件为存在一条定压边界，如边底水或存在注水井，当外边界补充的液量逐渐趋于井的产量时，地层内的压降曲线变化越来越小，直到地层各点压降下降速度趋于一致，此时则称为达到稳定渗流。

显然，对于煤层气储层来讲，由于没有边底水和注水井，煤层气开发属于衰竭开发，缺少了外边界液量的补充，煤层气井开发则不可能达到稳定渗流，故采用稳定渗流模型对渗透率进行计算与实际不符。

本文方法则充分考虑煤层气储层开发的实际情况，采用达到拟稳定流时的生产数据进行计算，所得结果更符合实际地层。

1.2.2 避免地层压力未知所造成的计算困难

采用产量公式推导得到渗透率计算模型，如文献[25]，均需要边界处的地层压力，即Pe。但在煤层井开发过程中该参数随时间变化而变化，且无法准确获得。造成采用文献中的公式无法准确获得渗透率值。

1.2.3 求解更方便

除了采用理论公式进行计算，研究人员还采用数值模拟的方法进行煤层气储层渗透率评价。但这两种方法计算过程均较烦琐，需要进行大量的拟合运算。

本文方法仅需要将煤层厚度、井筒半径等地层参数和产水量、井底流压等生产数据带入式(8)中，即可得到渗透率值，更方便现场人员使用。

同时，根据其推导过程，认为本文方法具有以下适用条件：本文方法适用于煤层气井出现拟稳定流时的排水降压阶段，所以为准确计算煤层渗透率，需要排水降压阶段缓慢降低井底流压压降速度，延长纯产水阶段的生产时间，以达到拟稳定渗流，避免压力过早低于临界解吸压力而出现两相流。

2 实例分析

A区块位于沁水盆地东南部，以3#煤层为主力煤层，当前开发程度较高。但区块内试井渗透率数据较少，仅有4口井获得了3#煤试井渗透率，为0.01～0.04 mD，平均为0.03 mD，其中AJ-005井3#煤层渗透率最小，仅为0.01 mD，但以上4口井注入压降试井均未达到径向流，渗透率解释结果并不可靠。

为了得到A区块渗透率分布规律，采用煤层渗透率拟稳定评价法进行渗透率计算。以AJ-224X2井为例，AJ-224X2井位于A区块(山西省晋城市沁水县)，于2017年11月23日压开3#煤层并排采，并于2018年1月14日开始产气，目前该井峰值产气量为698 m3/d，平均日产气499 m3/d，图2、图3所示为该井日产水和日产气曲线。取Re为150 m，等效半径Rwe为10 m，导压系数η为20 cm2/s。

针对所选区间的生产数据，利用物质平衡方程式(7)求得不同时间下的平均地层压力。其中原始地层压力取井底流压最大值，本例中为9.48 MPa，综合压缩系数取0.06 MPa，厚度为6 m，计算得到平均地层压力如图4所示。

将计算得到的平均地层压力、对应时间下的井底流压以及对应时间下的产水量代入式(8)中，计算得到不同时间下的渗透率，如图5所示。图6为基于文献[25]中的方法计算得到不同时间的渗透率值。

根据前文阐述，稳定渗流模型与煤层气井实际渗流方式相差较大，从计算结果上看，存在以下两个方面的问题：一是该方法需要将两个相邻时间步的产水量和井底流压之差作为输入参数，导致当井底流压下降时，产水量却未上升，则会出现渗透率为负值和零的情况(图4中部分计算结果出现负值)，造成计算得到的渗透率值无效；二是计算得到的渗透率分布区间较大，且无明显规律，导致无法准确判断地层的实际渗透率值。

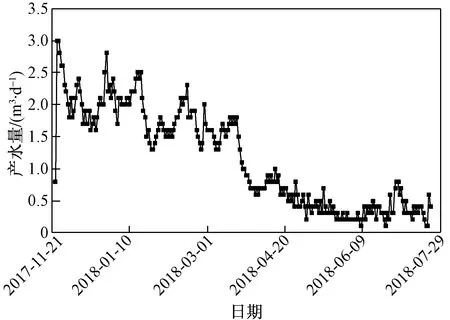
图2 AJ-224X2井日产水曲线Fig.2 Daily water production curve of AJ-224X2

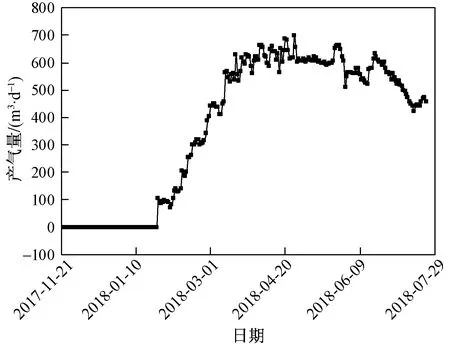
图3 AJ-224X2井日产气曲线Fig.3 Daily gas production curve of AJ-224X2

图4 平均地层压力计算结果图Fig.4 The graph of average formation pressure

图5 拟稳定法计算不同时间下渗透率图Fig.5 The permeability is calculated by pseudo-stability method at different time

图6 稳定法计算不同时间下渗透率图Fig.6 The permeability is calculated by stability method at different time

与稳定法对比，拟稳定法充分考虑了地层水在煤层中的渗流规律，并用平均地层压力代替边界处的地层压力，且计算过程只依赖于某一天的生产数据。从计算结果可以看到，渗透率波动较小，且无负值和零值情况出现，可信程度高。对拟稳定法计算结果取平均值，可知AJ-224X2井煤层渗透率值为0.21 mD。

基于煤层渗透率拟稳定评价法，对A区块其他6口井进行渗透率计算，图7为6口井不同排采时间下渗透率计算结果图。

图7 拟稳定法计算A区块排采井渗透率Fig.7 Calculation of permeability of drainage wells in block A by quasi stable method

计算结果再次表明，由于拟稳定法充分考虑了地层水在煤层中的渗流规律，渗透率计算结果波动较小，且无负值和零值情况出现，可信程度高。其中AJ-609X1井渗透率为0.6 mD，AJ-609井渗透率为0.25 mD，AJ-613X2井渗透率为0.7 mD，AJ-222井渗透率井0.91 mD，AJ-222X4井渗透率为0.97 mD，AJ-521X3井渗透率为1.8 mD。

基于以上对沁水盆地A区块渗透率的计算，形成该区块渗透率分布图，如图8所示，渗透率从西南方向向东北方向逐渐递减，西南区域渗透率可达到2 mD。

图8 A区块渗透率平面分布图Fig.8 Plane distribution of permeability in block A

从A区块当前产气量分布图可以看到，如图9所示，该区块煤层气井实际产气量同样从西南向东北方向递减，与渗透率变化方向一致，即高渗区高产，低渗区低产。进一步论证了计算所得到渗透率的准确性。

图9 A区块排采井产气量分布柱状图Fig.9 Gas production distribution histogram of drainage well in block A

3 应用前景

由于煤岩的特殊力学性质，以及试井成果缺乏且评价准确度较低，造成目前国内对煤储层渗透率的认识极不成熟，以至于在进行储层评价和产能预测研究时受到极大限制。提出一套基于拟稳定渗流的煤层气储层渗透率评价方法，该方法仅需利用生产资料即可反算煤层渗透率，并在中海油煤层气区块进行应用，首次认识了煤层气区块的渗透率分布规律。此外，该方法在煤层气开发领域有如下应用。

(1)为煤层气产能预测提供基础。当前，由于渗透率资料的缺乏，对煤层气井进行产量预测时造成了油藏人员“巧妇难为无米之炊”的窘境，本文方法为煤层气井产能预测提供了有力的资料基础。

(2)提高煤层气储层“甜点区”认识程度。当前，海油部分煤层气区块试井渗透率解释偏小(小于0.05 mD)，部分煤层气区块没有渗透率资料，导致当前认识的“甜点区”受到一定的限制，准确程度较差。基于本文方法精准评价煤储层渗透率，为“甜点区”的认识提高精度。

4 结论

(1)根据煤层气井压降规律，基于物质平衡原理、渗流力学等理论基础，建立煤层渗透率拟稳定计算方法，并形成相应的计算流程，分析本文方法优缺点及适用性。

(2)以沁水盆地A区块A1井为例，进行煤储层渗透率计算。结果表明，与稳定渗流法相比，拟稳定评价法计算结果波动较小，规律性更强，精确度更高。

(3)形成沁水盆地A区块渗透率分布规律，渗透率从西南方向向东北方向逐渐递减，西南区域渗透率可达到2 mD，变化趋势与排采井开发效果一致。