基于MUSIC 的分布式极化敏感立体阵列DOA 估计*

赵立鹏，姚国国，禹永植，陈 涛

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨150001；2.中国空空导弹研究院航空制导武器航空科技重点实验室，河南洛阳471009）

0 引言

共形阵列是指天线附着于载体表面且与载体贴合的阵列，可以与飞机、导弹以及卫星等高速运行的载体平台表面相共形。由于其具有节省空间、质量和不破坏空气动力学等特点，在电子侦察、电子干扰、航空航天及通信等领域引起了广泛关注。

分布式极化敏感阵列由于其单阵元多分量的特点，非常适用于空间受限的共形阵列。随着共形阵列的技术发展，分布式极化敏感阵列也得到了广泛应用，但目前的研究都是针对平面阵列，或是结构比较规则的球面、柱面和锥面立体阵列。文献[1]建立了锥面、柱面和球面的阵列模型，并将多重信号分类(MUSIC)算法[2]移植到上述模型中。文献[3]针对柱面阵列，实现了极化参数与DOA 参数的联合估计。文献[4]针对球面阵列提出了基于子阵分割的有向阵元MUSIC 算法。文献[5]针对柱面阵列，提出一种基于数据自适应子阵分割的快速DOA 估计算法，大幅度降低了运算复杂度，同时提高DOA 估计精确度。若共形阵列的载体有特殊要求，以上模型不再适用，需要更灵活的天线摆放形式，同时由于每个天线的单一极化特性，多极化接收也需要通过天线的不同摆放来实现。此时，共形阵列的摆放形式可能不再是同一平面内摆放或规则的立体摆放，国内外学者在此方面研究较少，故本文提出了分布式极化敏感立体阵列的模型，可以实现阵元在三维立体空间内任意摆放。

随着DOA 估计技术的发展，包括MUSIC、ESPRIT 和Root-MUSIC 等DOA 估计算法移植到极化敏感平面阵列的应用已经比较成熟，但是ESPRIT 和Root-MUSIC 等算法只对特殊阵列有效，而MUSIC 算法对阵列有着普遍的适用性，可以移植到多种阵列中。文献[6]首次将MUSIC 算法移植到极化敏感阵列，对数据进行4 维联合DOA 估计即可求出信号的DOA 和极化参数。在此基础上，为了减小计算复杂度以及提高测角精度，诸多学者对算法进行改进，文献[7]使用秩亏MUSIC 方法将角度域和极化域的四维搜索变为2 个分别唯角度域和唯极化域的二维搜索，实现了到达角和极化参数的四维参数估计。针对分布式极化敏感立体阵列的DOA 估计问题，本文将极化MUSIC 算法移植到了分布式极化敏感立体阵列的模型中，同时提出了相应的通道幅相误差校正方法，实现了到达角参数和极化参数的联合估计。

1 分布式极化敏感立体阵列

以下为阵列模型的假设条件：

1）入射信号均为远场源信号。

2）各阵元接收噪声为高斯白噪声，噪声之间以及噪声与信号之间相互独立。

3）各阵元为单偶极子，线极化方式接收信号。

4）各天线的波束指向一致。

1.1 阵列几何结构

分布式极化敏感立体阵列的几何结构如图1 所示，阵列中各阵元为单偶极子，分布在三维空间内。并且各阵元指向不同，对不同极化状态的入射信号有不同的响应，可以达到敏感极化信息的目的。

图1 分布式极化敏感立体阵列几何结构

各天线波束指向一致，不再考虑摆放滚转角，定义天线摆放角为(α,β)，其中α 为共形天线在XOY 平面的投影与X 轴的夹角，β 为共形天线与Z 轴的夹角，如图2 所示。在一般的分布式极化敏感平面阵列中，β为固定值，而在立体阵列中，随着各天线的灵活摆放β会随之变动。

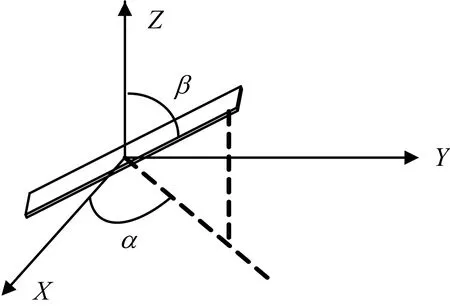
图2 共形天线与摆放角定义

1.2 分布式极化敏感立体阵列接收模型

假设有M 个远场窄带信号入射到该阵列中，其中第m 个入射信号的到达角和极化参数分别为(θm,φm,γm,ηm)，立体极化敏感阵列的信号接收模型可以表示为：

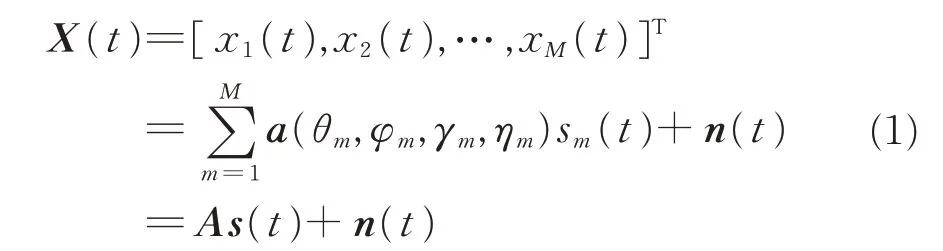
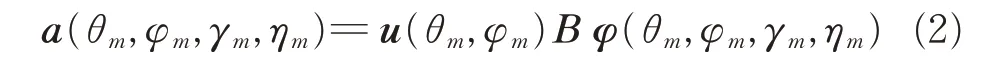
式中，u(θm,φm)为第m 个信号的阵元空间相位矩阵。

式中，diag [·]表示对角矩阵，un(θm,φm)为第n 个阵元处，第m 个信号形成的空间延迟：

式 中，ω=2πc/λ，c 为 光 速，λ 为 信 号 波 长。τn=(xnsinθmcosφm+ynsinθmsinφm+zncosθm)，为信 号 在第n 个阵元与原点之间的空间延迟。(xn,yn,zn)为第n个阵元相对于原点的坐标。

式(2)中，B 为极化敏感矩阵，与各阵元的摆放有关。设入射信号与天线极化完全匹配时的增益为1，则天线的增益矢量为：

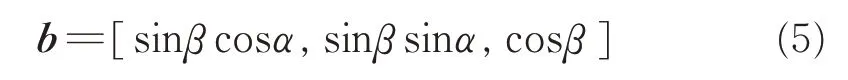
对于分布式极化敏感立体阵列，极化敏感矩阵B 为：

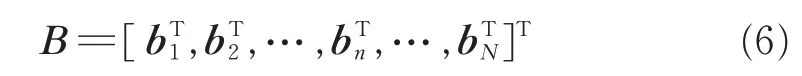
式(2)中，φ(θm,φm,γm,ηm)描述了极化域与角度域的相干结构，如图3 所示，与每个极化敏感阵元的位置无关。在分布式极化敏感立体阵列中可以表示为：

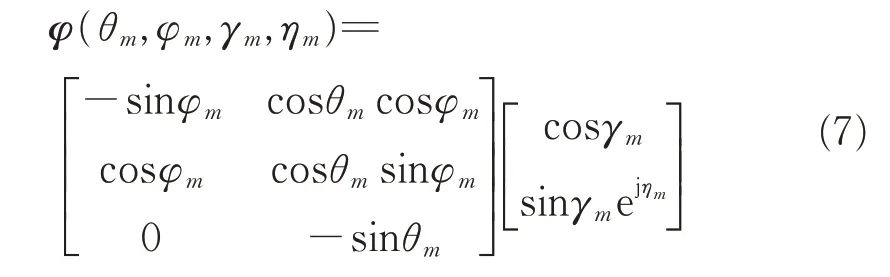
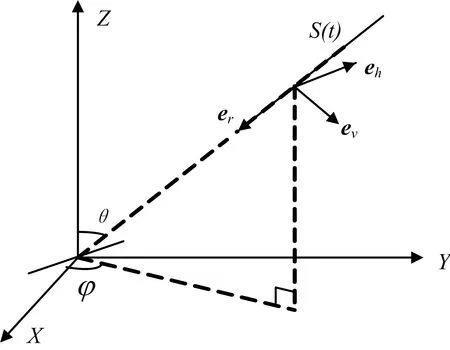
图3 极化域与角度域的相干结构

将u(θm,φm)，B 和φ(θm,φm,γm,ηm)的具体形 式 代入式(2)即可得到导向矢量的具体形式。

2 极化MUSIC 算法

基于以上给出的分布式极化敏感立体阵列的信号接收模型，将极化MUSIC 算法拓展到此模型中，根据导向矢量的形式构造达到角和极化参数联合谱，估计信号参数。

2.1 极化MUSIC 算法原理

假设有M 个远场窄带完全极化信号入射到由N个阵元组成的阵列中，对信号x(t)采样K 次并构造协方差矩阵：

对协方差矩阵进行特征值分解可得：

式中，US为信号子空间，由M 个大特征值对应的特征向量[u1,u2,…,uM]构成。UN为噪声子空间，由N-M个小特征值对应的特征向量[uM+1,uM+2,…,uN]构成。根据信号子空间与导向矢量及噪声子空间的关系有：

因此，导向矢量和噪声子空间存在正交的关系，根据此关系，构造谱密度函数：

在4 个参数(θ,φ,γ,η)张成的四维空间中，通过谱峰搜索获得谱峰位置坐标值，即可得到信号的到达角和极化参数估计值。

2.2 到达角和极化参数估计

由以上得到的谱密度函数，需要进行四维搜索谱峰值才可以得到四维参数的估计值，运算复杂度比较高，运算量非常大。下面介绍一种结合秩亏原理的极化MUSIC 方法，将四维空间搜索化简为唯角度域和唯极化域的2 个二维空间搜索。

根据导向矢量和噪声子空间的正交关系，有：

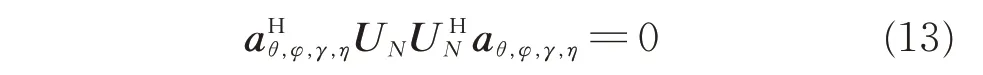
而aθ,φ,γ,η可以改写为：

进一步，式(13)可以改写为：

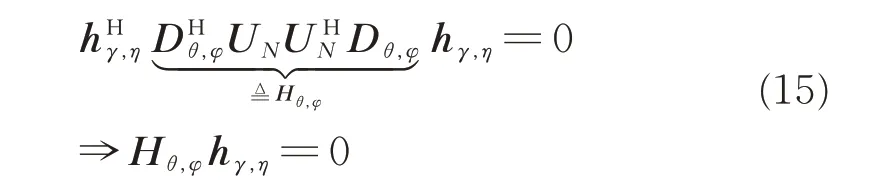
由于hγ,η为满秩 矩阵，若式(15)成立，则Hθ,φ必为亏秩矩阵，也就是当即满足M组真实入射信号的到达角参数时，上式成立。由此，到达角参数的谱函数搜索可以表示为：

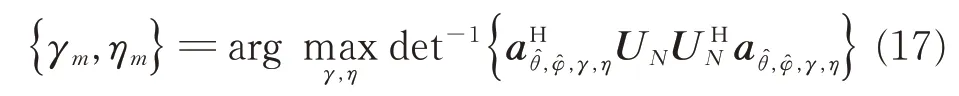
经过2 次二维搜索后得到M 组到达角估计值和M组极化参数估计值。

当多个信号入射时，需要对到达角参数和极化参数进行配对。根据正确配对的参数谱密度值必定会大于其他配对错误时参数谱密度值的原理，以2 信号入射为例，即：

使用秩亏极化MUSIC 方法得到入射信号的到达角和极化参数估计值后再使用此判断法对谱密度大小进行判断，即可得到入射信号的正确配对参数。

2.3 通道幅相误差校正

在极化敏感立体阵列中，由于极化参数以及阵元三维摆放的影响，针对传统标量平面阵列的幅相误差校正方法不再适用，下面给出基于分布式极化敏感立体阵列的通道幅相误差校正方法。

基于图1 所示的八阵元分布式极化敏感立体阵列，当阵列存在幅相误差时，阵列接收到的信号形式与式(1)不同，可以表示为：

式 中 ， W =diag[ g1exp(jφ1),…,gnexp(jφn),…,gNexp(jφN)]为通道幅相误差矩阵，gn和φn分别表示第n 个通道的幅度增益和相位误差。

1）消除固有影响

①极化参数影响。分布式极化敏感阵列中，与传统标量阵列不同的是，极化参数的加入会对各通道的幅相带来一定影响，由分布式极化敏感立体阵列的模型可以得出极化参数的影响P 可以表示为：

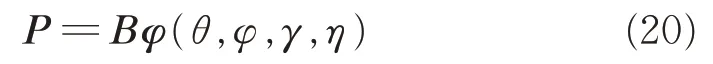
②纵轴空间延迟影响。除极化参数的影响外，立体阵列由于阵元在三维空间内摆放，与平面阵列相比，各阵元接收信号在纵轴方向的不同空间延迟也会对各通道幅相造成影响。

为消除这两部分影响，使用静态校正的方法，用已知极化和入射角度的辅助源，假设极化与角度已知且到达角为(θ,φ)=(0°,0°)，极化方式为圆极化的辅助源，将参数代入式(2)可得此时导向矢量为：

式中，Z 为0°信号入射立体阵列时纵轴方向达到角参数的影响，P 即为极化参数带来的影响，这两部分总影响I=Z.*P，“.*”代表矩阵对应元素相乘，计算消除两部分总影响后接收数据协方差矩阵

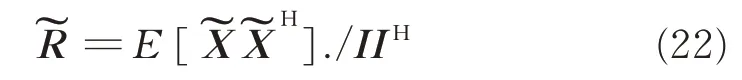
2）幅相不一致补偿

消除固有影响后，再对通道的幅相不一致进行补偿。

以第1 个通道为参考，W 可以变换为：

式 中 ，W′=diag [1,g2/g1exp(j(φ2-φ1)),…,gN/g1exp(j(φN-φ1))]为以第1 通道为参考的幅相误差矩阵。由式(23)可得存在幅相误差的阵列接收数据协方差矩阵可以表示为：

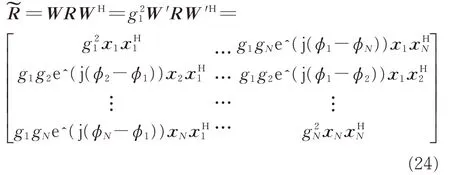
式中，R 是消除固有影响且不存在通道幅相误差时的阵列接收数据协方差矩阵。理想条件下，在只有一个0°入射信号时，R 中的元素满足(i,j=1,2,…,N )，xi为不存在幅相误差时第i 个通道接收的数据，可以得到：

通道幅相误差校正方法总结如下：

1）使用一个到达角参数为(0°,0°)，极化方式为圆极化的辅助源，根据式(22)计算阵列接收数据消去固有影响的协方差矩阵

3）根据式(27)校正公式对导向矢量矩阵进行校正，得到校正后的导向矢量矩阵再进行入射信号的参数估计。

3 仿真实验

采用模型为图1 所示的八阵元分布式极化敏感立体阵列，每个阵元的位置坐标(x,y,z)分别为（0.1，-0.05，-0.01），（0.15，0.03，-0.03）（0.1，0.08，-0.04），（0，0.1，-0.05），（-0.1，0.08，-0.04），（-0.15，0.03，-0.03），（-0.1，-0.04，-0.01），（0，-0.1，0），坐标单位为m。第n 个阵元的摆放角为αn=360°n/8，βn=90°n/8。基于此阵列进行以下计算机仿真。

3.1 通道幅相误差校正

假设单信源入射到阵列中，信号到达角和极化参数为(θ,φ,γ,η)=(30°,40°,20°,35°)，快拍数为100，信噪比为15 dB，频率为4 GHz，使用极化MUSIC 算法仿真得到幅相误差校正前后的参数估计结果如图4—7所示。

假设单信源入射到该阵列，信源到达角参数在±60°内随机给出，极化参数为(γ,η)=(45°,20°)，入射信号信噪比分别为0 dB、4 dB、8 dB、12 dB、16 dB、20 dB 时，快拍数为100，搜索步进为0.2°。在校正前后使用极化MUSIC 算法各做100 次Monte-Carlo 实验，得到不同信噪比下的单信源均方根误差如图8 所示。

估计均方根误差(RMSE)定义为：

图4 校正前DOA 估计结果

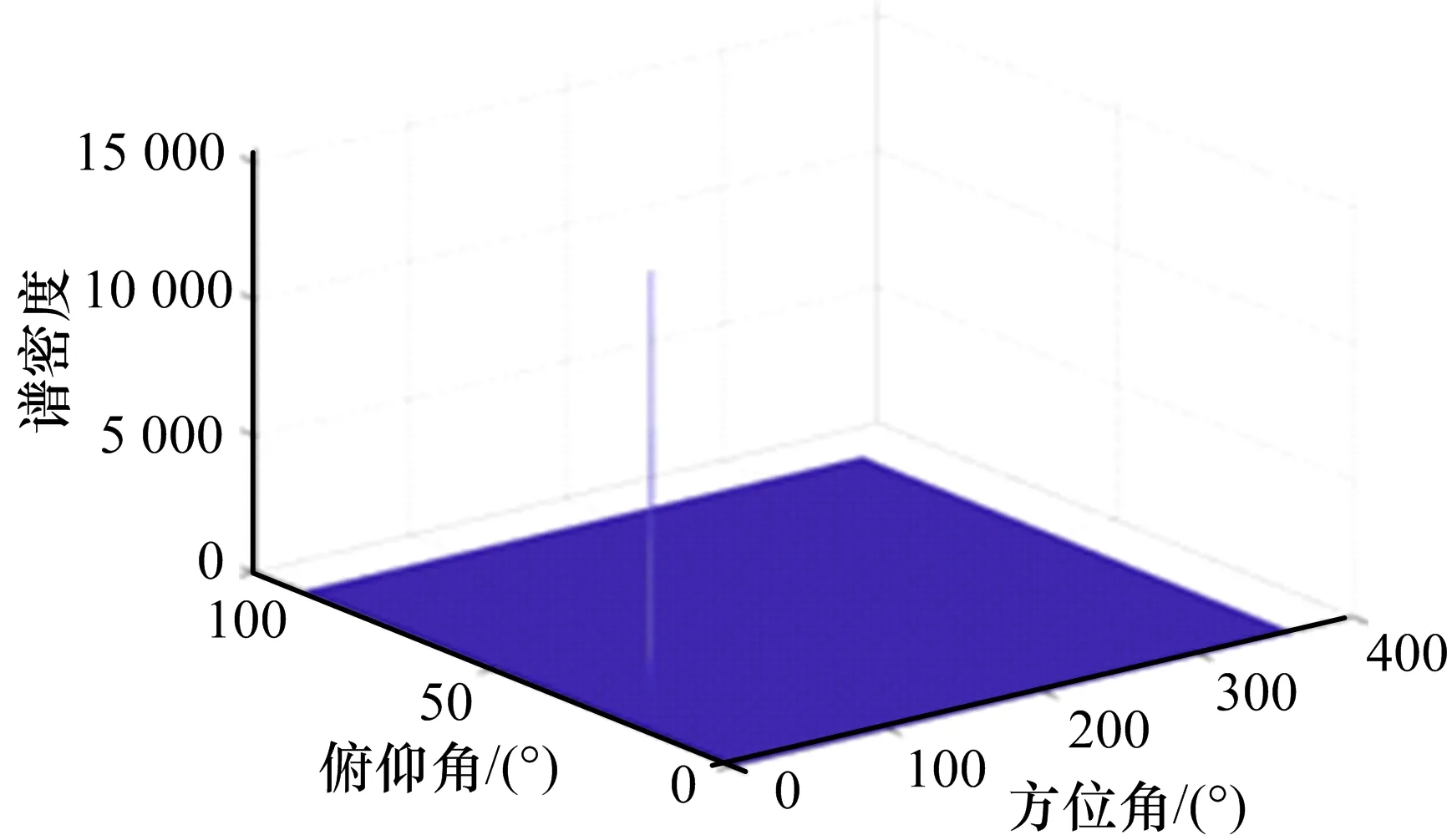
图5 校正后DOA 估计结果

图6 校正前极化参数估计结果

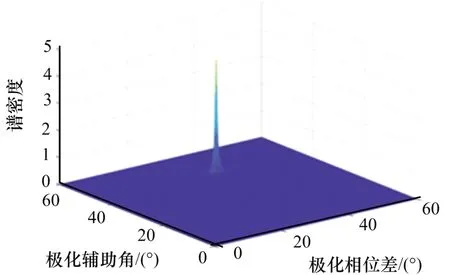
图7 校正后极化参数估计结果

式中，N 为Monte-Carlo 实验中测向结果正确的次数，θ和φ 的估计值与真实值的差值均在2°以内视为测向正确。分别为俯仰角和方位角的估计值，θ 和φ 为俯仰角和方位角的真实值。

图8 幅相误差校正前后均方根误差

由图4—7 可以看出，幅相误差校正后谱峰明显尖锐许多，DOA 估计结果更加准确，证明了通道幅相误差校正方法的正确性。且由图8 可以看出，经过通道幅相误差校正后的测角精度得到明显提高。

3.2 测角性能比较

假设单信源入射到该阵列，信源到达角参数在±60°内随机给出，极化参数为(γ,η)=(45°,20°)，入射信号信噪比分别为0 dB、4 dB、8 dB、12 dB、16 dB、20 dB 时，快拍数为100，搜索步进为0.2°。使用极化MUSIC 算法以及传统MUSIC 算法各做100 次Monte-Carlo 实验，得到不同信噪比下的单信源均方根误差如图9 所示。

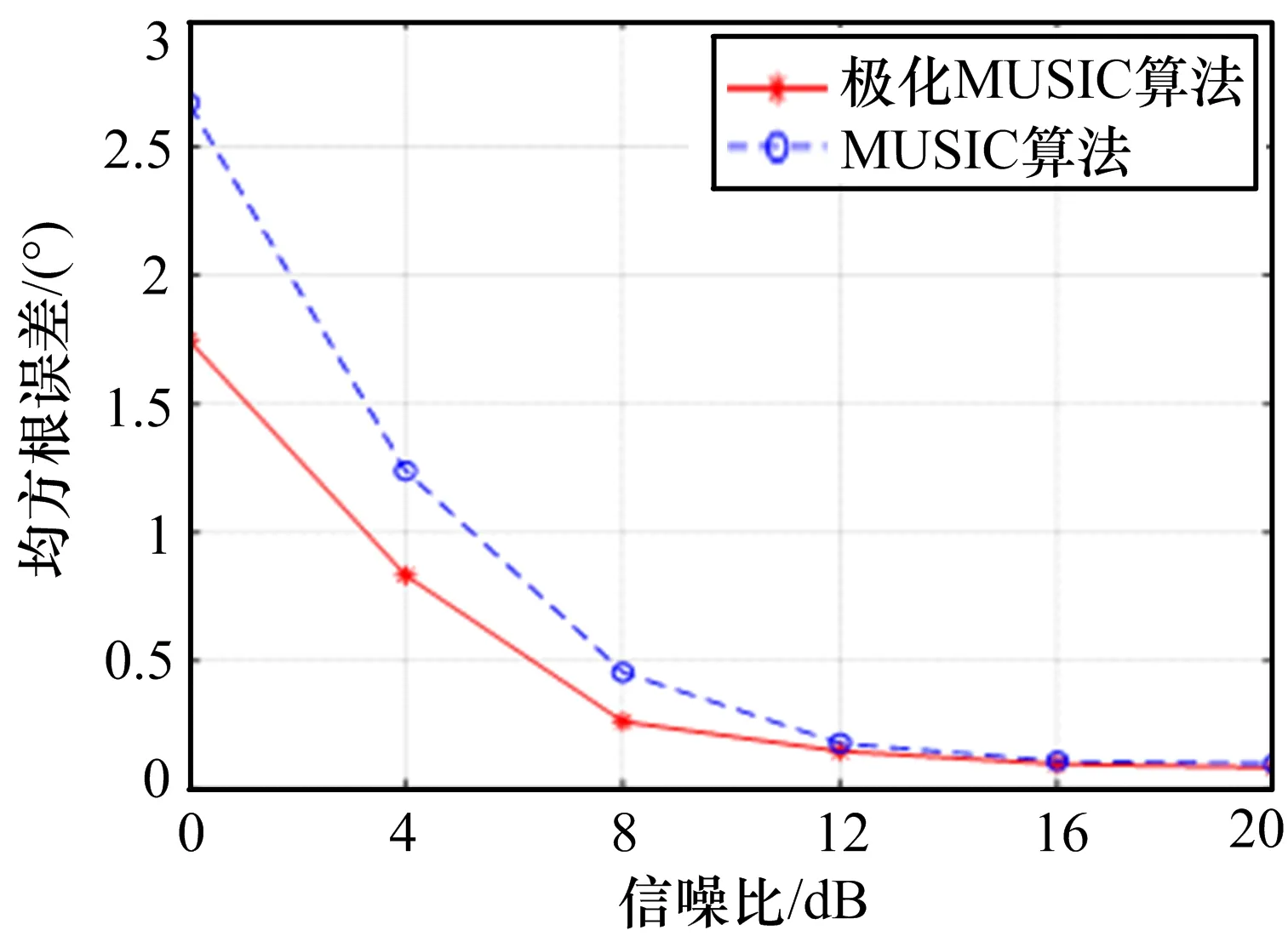
图9 均方根误差随信噪比变化情况

由图9 可以看出，极化MUSIC 算法的测角性能要优于普通标量阵列下的MUSIC 算法，尤其在低信噪比的情况下，且随着信噪比增大，均方根误差逐渐减小，DOA 的估计性能也越好。

3.3 分辨力比较

假设有2 个信源同时入射到该阵列，信源a 的到达角和极化参数为(θ,φ,γ,η)=(θ1,φ1,45°,20°)，信源b 的 参 数 为(θ,φ,γ,η)=(θ1+Δ,φ1+Δ,20°,30°)，(θ1,φ1) 在 ±60° 内 随 机 给 出 ，Δ 分 别 取±1°、±1.5°、±2°即比较对极化参数不同但到达角只相差Δ 情况下的2 信号分辨情况。入射信号信噪比为5～20 dB，频率为4 GHz，快拍数为100。θ 和φ 的估计值与真实值的差值均在2°以内视为测角成功。使用极化MUSIC 算法和传统MUSIC 算法各进行1 000次Monte-Carlo 实验，得到不同信噪比下测角成功率如图10 所示。

图10 不同信噪比下2 信源测角成功率

由图10 可以看出，极化MUSIC 算法可以在2 信源角度间隔1°及信噪比15 dB 以上时达到99%测角成功率，分辨力远优于普通标量阵列下的MUSIC算法。

4 结束语

本文提出了一种分布式极化敏感立体阵列。首先给出了该阵列的几何结构并建立了接收信号的数学模型，之后将适用于极化敏感平面阵列的秩亏极化MUSIC 算法移植到立体阵列中，并采用静态校正的方法对通道幅相误差进行校正，即先消除固有影响后补偿通道幅相不一致，实现了到达角和极化参数的联合估计。相较于平面阵列和锥面、球面、柱面立体阵列，本文提出的阵列模型摆放形式更加灵活，可以更方便地应用于共形阵列。■