基于证据可信度的多传感器多目标融合识别方法

贾正望，张 亚

（中国电子科技集团公司第二十八研究所，江苏南京210007）

0 引言

多传感器多目标的融合识别是将系统中多套传感器独立提供的识别结果进行决策级融合，产生比单一传感器更有效、更精确的身份估计和判断[1]。对于导弹防御系统中的多传感器融合识别系统而言，由于每部雷达或红外探测系统所处环境往往复杂多变，且不同目标的传感器特性差异较大，指控系统在融合多部雷达的识别结果时，如何确定传感器的可信度非常困难。不同波段的雷达或红外探测系统，在识别弹头、诱饵或假目标时的可信度差别很大，比如P 波段雷达信号带宽低，只具备初步识别能力；X 波段雷达因为信号带宽大、波形多样，所以识别结果相对更为准确。而指控系统在缺乏目标特性原始信息的情况下，如何仅依赖单装识别结果，进行传感器可信度的评估，以提升融合识别有效性就显得非常重要。影响单一传感器识别可信度大小的因素有：传感器观测信息在目标特征空间里的可分离性；本地分类识别方法的正确率；传感器识别结果序列的一致性；各传感器观测信息之间存在的相关性。

D-S 证据理论作为一种有效的手段，对决策级多传感器融合识别有较好的优势，能够很好地处理识别结果未知和不确定，近年来在融合目标识别方面，证据理论逐渐得到了应用[2-7]。但常规D-S 组合规则融合识别证据时，通常认为各传感器识别证据的信任程度是相同的，这并不符合实际。引入传感器可信度作为融合的权值，定量地反映被融合信息的质量，可信度高的识别结果赋予较高的权值，反之赋予较低的权值，这样增加了可靠传感器（比如X 波段雷达）的优势，削弱了弱势传感系统（比如P 波段雷达）对最终结果的影响，有效地减少了系统的不确定性。

1 D-S 证据理论

D-S 证据理论[8]是由Dempster 和Shafer 提出并发展起来的一种不确定性推理方法。它最大的特点是对不确定信息的描述采用了“区间估计”而不是“点估计”的方法，在区分不知道与不确定方面以及精确反映证据收集方面显示出很大的灵活性。

设Θ 为识别框架，如果集函数m:2Θ→[0,1]（2Θ为Θ 的幂集）满足则称m 为识别框架Θ 上的基本信度分配；∀A ⊂Θ,m(A)称为A的基本概率赋值函数(BPAF)。m(A)反映了对A 本身的信任度的大小。

关于证据合成与推理，D-S 证据理论给出了如下规则：

设m1、m2分别对应同一识别框架Θ 上的信度函数分 配，焦 元 分 别 为A1,A2,…,Ak和B1,B2,…,Bk，设则由下式定义的函数m:2 →(0,1)是联合后的信度函数分配：

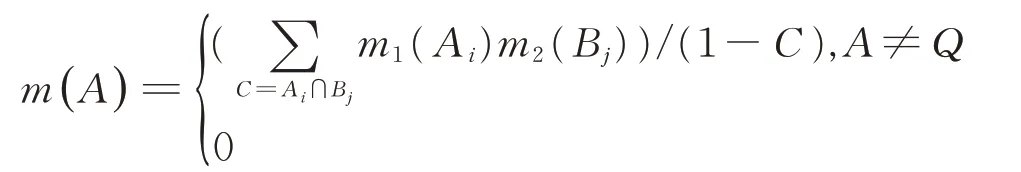
BPAF 的赋值是融合识别中非常重要的一个环节，直接影响到融合结果的准确性和可靠性。一般来说，基本概率赋值没有明确的规则，大多依靠专家经验或者领域知识进行基本概率赋值。针对融合多传感器目标识别的具体情况，从距离和相关性度量角度出发，基本概率分配函数定义如下：

1）距离和相关性度量

设证据体(传感器)I 的特征向量为Xi，目标(监测类型)Aj的标准样本特征向量为Yj.则两者的Manhattan 距离为：

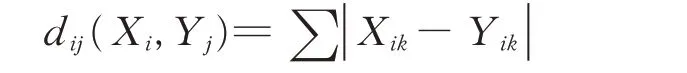
距离dij(Xi,Yj)越大，则证据体i 与目标Aj的相关程度越低；反之，距离dij(Xi,Yj)越小，则证据体i与目标Aj的相关程度越高，因此，定义有：

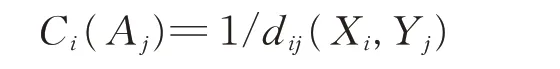
证据体与目标的最大相关性为：ai=max {Ci(Aj)}=1/min {dij(Xi,Yj)}

证据体i 与各目标相关系数的分布系数为：

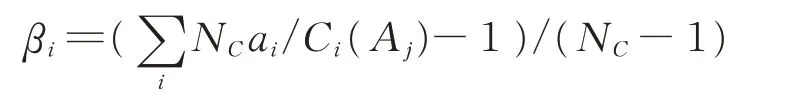
式中，N 为待测目标类型数。

证据体（传感器）i 的可靠系数为：

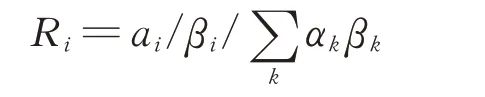
2）基本概率分配函数BPAF 的构造

综合上面公式得到证据体i 赋予目标Aj的基本概率分配以及赋予识别框架Θ 的基本概率分配，即传感器的不确定性概率值的算法如下：

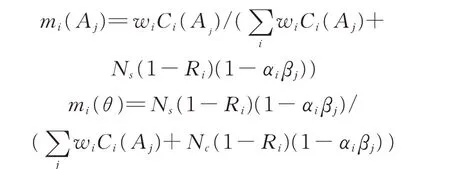
式中，Ns为传感器数目；wi为加权系数，根据相关系数Ci(Aj)的大小取值，且0＜wi＜l。

上面2 式，建立了证据体(传感器)与目标(监测类型)之间距离与相关性的对应关系和相关性的分布，以及传感器可信度系数，又根据证据体与目标的相关性引入了加权系数。

2 基于证据可信度的融合识别

实际防空反导系统中，各类雷达、红外传感系统由于受到各种环境因素的影响和传感器测量范围以及精度等自身条件的限制，各种量测在一定程度上存在不准确和不完善，其信任等级程度是不同的。假定某单一传感器对动态目标的识别过程是动态变化的，但识别报告也应具有高度的一致性。可以认为，一致性高具有较高的可信度，反之可信度较低。为了解决多传感器综合目标识别中不同等级信息源数据的融合问题，在研究D-S 证据理论的基础上，本文提出基于一致性假设的多传感器融合识别证据可信度计算方法，来修正常规的基本概率赋值函数，并构造基于可信度的D-S 证据合成方法。

假设某传感器单元在不同时刻点得到某个目标的一组识别报告gi，在估计该传感器对该目标识别权值系数过程中，识别结果一致性越好，数值越接近中心，认为其可信度越高。换句话说，中心点的估计是gi的加权平均值。为了近似gi中心值，用不同的gi之间的相对冲突来确定。每个gi之间的冲突用相对冲突矩阵D=[dij]n×n来计算和表示，其中dij=|gi-gj|，dii=0，dij=dji。对于每个gj，相对冲突的平均值由计算。用平均冲突来测量gi对数据中心的近似程度的值越小，gi的值越接近中心在估计时的加权越大。

设mi和mj是同一传感器不同时间段识别结果处理得到的基本概率分配函数，mi和mj相对冲突距离定义为：

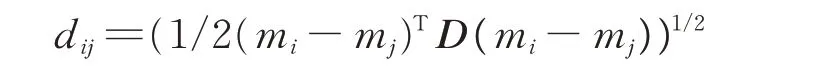
式 中，D 是 一 个2N×2N矩 阵，其 元 素 为D(A，B)=|A ∩B |/| A ∪B |，A，B ∈2Θ，|·|表示该属性所包含的元素个数。

若选取的时间点序列个数为n，计算其中各个证据体间的距离，获得距离矩阵：

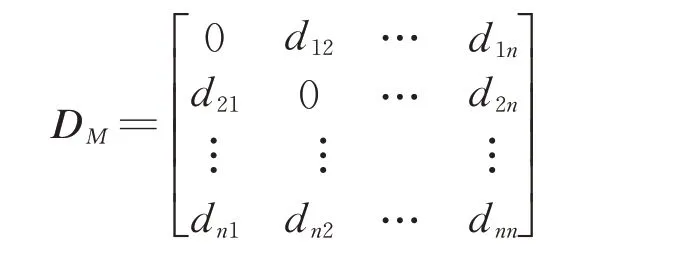
则第i 个证据到证据集中其他证据的均方根距离为：

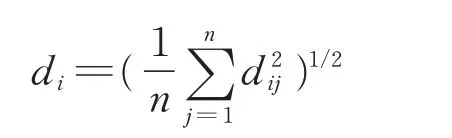
式中，di反映了此识别证据与证据集中其他证据的差异程度。

定义第i 个识别证据的可信度因子为：

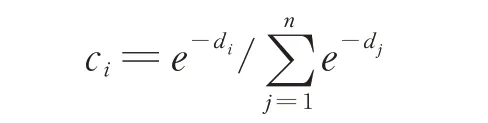
式 中，di、dj分 别反映 了第i、j 个 证据与其他证据的差异程度。对可信度因子进行归一化：

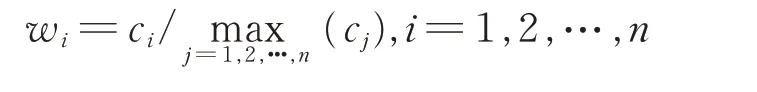
若某一证据归一化后的可信度为1，表示其受支持程度最高。

wi作为第i 个证据的归一化可信度因子，对原始证据集的基本概率分配函数进行修正，若原始第i 个证据的基本概率分配函数为mi=[mi(A1),mi(A2),…,mi(As),…,mi(Θ)]，则修正后的基本概率分配函数为：

3 融合识别流程

多传感器融合目标识别是将由系统中多个传感器提供的关于目标身份的信息进行综合，产生比系统中单一传感器更有效、更精确的身份估计和判决。由于传感器对不同目标的识别率和传感器工作时所受干扰的不同，所提供证据的可信度存在差别，为了充分体现不同传感器对证据合成的贡献，同时在融合之前过滤掉明显错误的数据。决策级融合识别框中传感器可信度估计和融合识别方法如图1 所示。

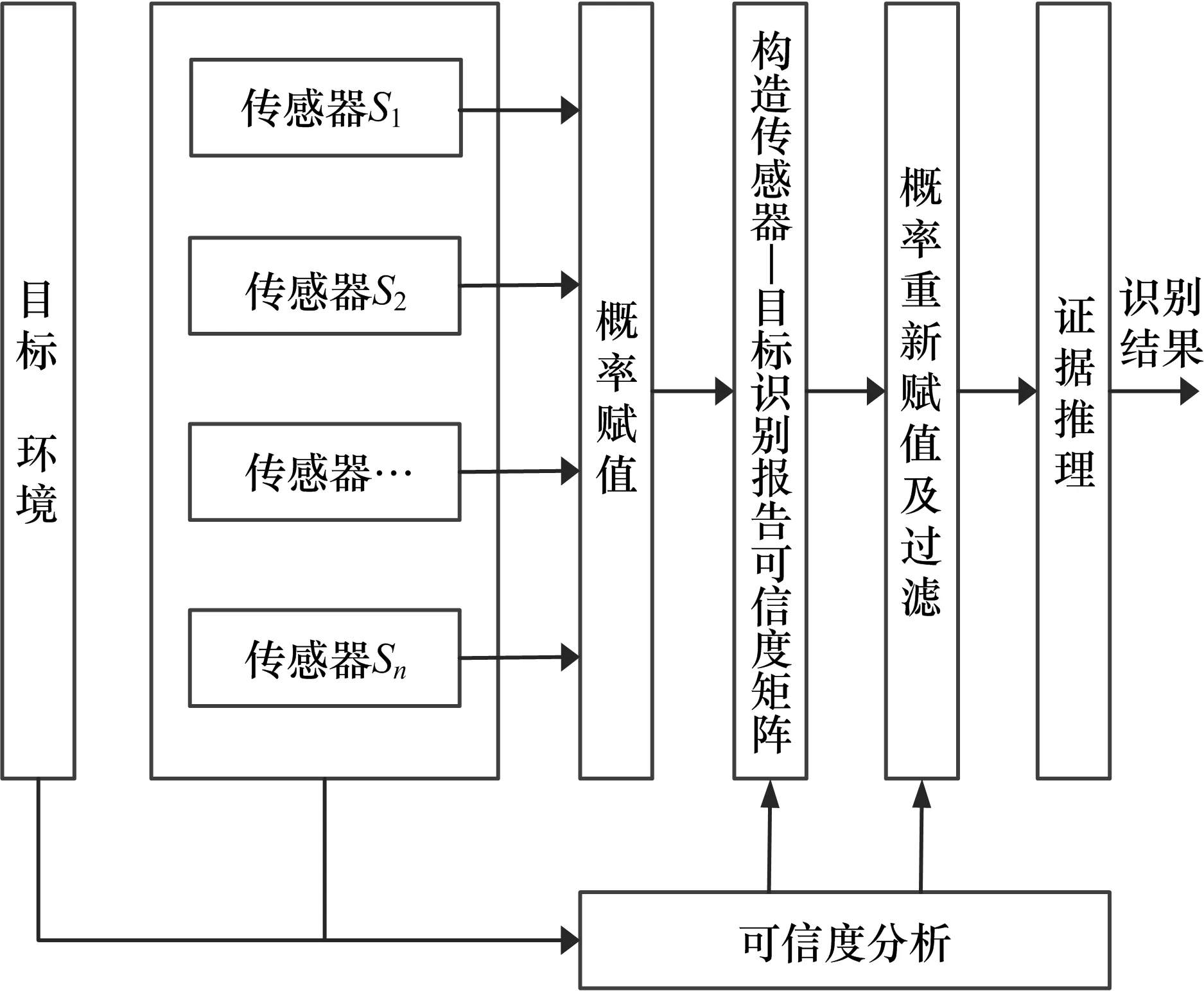
图1 基于传感器可信度的融合识别框架

目标因素和环境因素导致的各传感器之间识别报告存在的不一致性，可用识别报告的冲突系数来度量。识别证据之间的相对冲突可以部分反映证据之间的关联程度，通过求解特征向量可以得到证据的相对权重和各个证据的折扣系数，利用折扣系数方法可以有效解决冲突证据融合。

基于可信度的多传感器融合识别流程如下：

1）根据待识别系统特点构造辨识框架。

2）根据传感器提取的特征选择证据体。

3）构造证据体基本概率分配函数mn。

4）基于传感器的数据进行可信度分析，得到第j个传感器对第i 个传感器的归一化可信度因子wi。

5）对3）中得到的基本概率分配函数mn与4）中得到的每个证据体权系数wi，计算得到加权后基本概率分配函数Wmi(Ak)=wimi(Ak)。

6）由5）中得到的Wmi，根据可信度的D-S 证据理论的合成规则对数据进行融合：

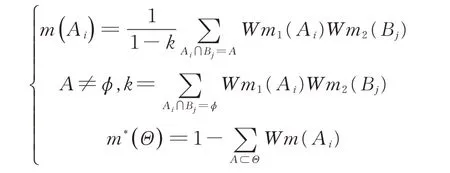
7） 对 6） 中得到的 m(Ai)，令 m(A1)=max {m(Ai),Ai⊂Θ }，m(A2)=max {m(Ai),Ai≠A1}，进行模式识别决策，若有：

则A1即为最终判定结果。

4 实验和分析

识别系统中设定3 类传感器：雷达（Radar）、红外（IR）和电子战（ESM），目标识别框为θ(h1,h2,h3,h4)，h1表示弹头，h2表示诱饵，h3表示假目标，h4表示干扰源，模拟各传感器识别结果。输入到识别系统的还有其他信息：天气的好坏、目标的远近、外部的干扰等。

利用专家经验对基本概率赋值，如表1 所示，其中IR 对干扰源判断出现虚高。估计IR 本地识别信息的λ=0.46，ESM本地识别信息的λ=0.78，Radar 的λ=1。

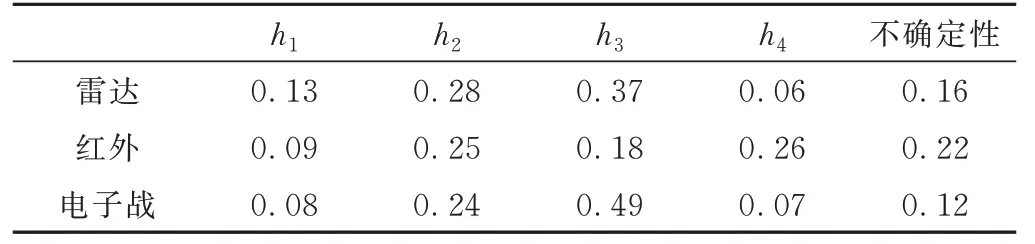
表1 基本概率赋值

仿真过程对数据进行了非可信度加权融合和可信度加权融合，实验1 为非可信度加权融合，实验2 为可信度加权融合。结果如表2 所示。

表2 可信度融合估计结果

对实验结果进行分析发现：实验1 对传感器未进行可信度加权情况下，诱饵和假目标数据较为接近，接近率达56.2 %，对识别结果判断的准确性可能会带来影响。实验2 对传感器进行一致性可信度加权后，诱饵和假目标数据进一步拉大，接近率只有36.5 %，能帮助提高识别结果的正确性。

5 结束语

在实用的多传感器融合识别系统中，为尽量减少对人工经验的依赖，如何有效融合多部雷达的识别结果，并提升在指控系统中目标综合识别的自动化程度，意义重大。本文在常规D-S 证据理论融合多传感器目标识别的框架基础上，定义了一种基于一致性假设的可信度定义和度量方法，以引入传感器可信度来改善基本概率赋值函数，并修正D-S 证据组合方法。仿真了多传感器多目标的识别场景，并将2 种方式的融合算法进行了对比，实验证明引入可信度度量可以有效地提升识别的可区分度和正确率。■