相似三角形的基本模型分类解析
2020-02-03王晓兰
王晓兰


相似三角形是初中数学的重要知识点,也是各地中考命题的重要考点.解决相似三角形的有关问题,关键是要寻找或构造出相似三角形的基本模型,再运用相似三角形的有关性质来处理.下面以中考试题为例,对常见的相似三角形基本模型进行分类解析,供大家学习时参考.
基本模型l:“A”型
例1 (2019.贺州)如图1,在△ABC中,D,E分别是AB.AC边上的点,DE //BC.若AD=2,AB=3,DE =4,则BC等于(
).
A. 5
B. 6
C. 7
D. 8
点评:由平行线可以得到“A”型的相似三角形基本模型,利用相似三角形的对应边成比例列式即可解决问题.
解析:8由平行四边形可以得到平行线,进而可以发现△AEF和△CBF是“X”型的相似三角形,根据相似三角形的性质列式计算即可,注意到点E将AD分为2:3的两部分,因此有A E:ED=2:3和AE:ED=3:2两种情况,如图2,所以要分类讨论求解,
点评:由平行线可以得到“X”型的相似三角形基本模型,利用相似三角形的面积比等于相似比的平方即可解决问题.由于点E将AD分为2:3的两部分有两种情况,所以要注意分类讨论,谨防漏解,
点评:本题△ECD与△FCE具有旋转缩放的对应关系,其一般形式是:如圖6,若∠BAC=∠DAE.∠B=∠D.则△ABC∽△ADE.实际上,△ADE是由△ABC绕点A旋转一定的角度后放大得到的,其中∠BAD是旋转角.
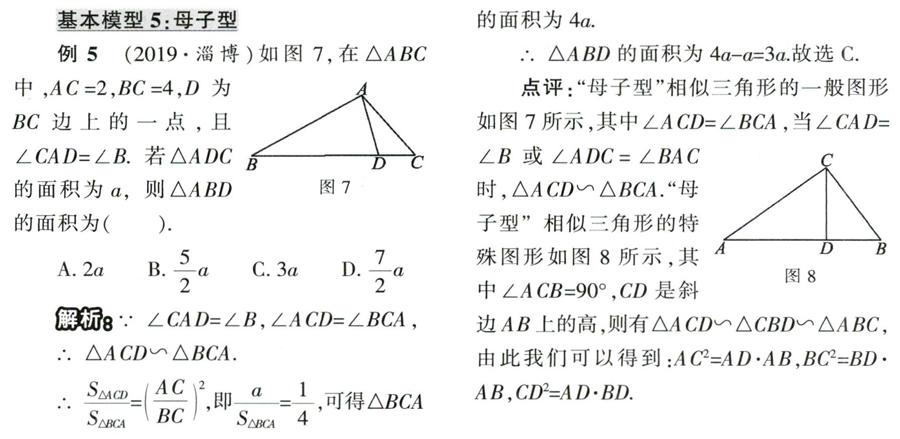
点评:“母子型”相似三角形的一般图形如图7所示,其中∠ACD= ∠BCA,当∠CAD=∠B或∠ADC=∠BAC时,△ACD∽△BCA.“母子型”相似三角形的特殊图形如图8所示,其中∠ACB=90°.CD是斜边AB上的高,则有△ACD∽△CBD∽△ABC,由此我们可以得到:AC2=AD.AB,BC2=BD.AB, CD2=AD.BD.
