大规模海上风电场内部电气汇集系统设计方案经济性优化
2020-02-03张明耀李雨佳尹忠东
张明耀, 廉 伟, 李雨佳, 尹忠东*
(1.国网山东省电力公司烟台供电公司, 烟台 264000; 2.华北电力大学电气与电子工程学院, 北京 102206)
随着经济的发展,用电量的增加,煤炭等非可再生能源的消耗量越来越大,因为其不可再生且对环境有污染,所以新能源发电技术越来越受到重视。风能作为世界上的清洁能源之一,它分布广又是可再生能源,因此风力发电技术是现在的研究热点。截至2016年,全球累计装机容量已经达到48 349 MW;欧洲的海上风电场技术领先,海上风电技术发展迅速,海上风电场的规模日益增大,到2025年,欧洲海上风电总装机量达到40 GW;中国海上风电是未来风电行业的重点发展方向,根据中国海上风电规划发展趋势,到2030年,海上风电交实现超过 3 000×104kW装机[1-2]。如何将日益增大的机组容量汇集送出以及如何实现海上风电的并网也成了当下研究的热点。海上风电场一般建设在离岸10~70 km,通常离岸较近时适合采用交流输电的方式并网,离岸较远则适合采用高压直流的方式输送。随着海上风电的规模增大,海上风电汇集送出系统需要花费更多的成本,包括投资成本、维护成本以及损耗成本,一般比陆上风电场要高出2~3倍[2-3]。针对海上风电场经济性等问题,文献[3]对海上风电现如今典型的输送方案进行了投资经济性对比分析,比较结果表明随着距离的增加,高压直流(HVDC)的经济性明显优于高压交流(HVAC)输电方式。结论仅适用于一般参考,没有进行具体拓扑分析。文献[4]将海底电缆采用现金流折现模型,进行成本分析作为判断交流输电方式和直流输电方式经济性的依据,但没对成本问题进行优化。文献[5]分析了江苏如东海上风电并网方式及其对应拓扑的投资、维护、损耗成本,比较了交流输电系统、直流输电系统、交直流混合输电系统的总成本,但没对相应的拓扑进行成本优化。文献[6]利用无功-电压Q-V曲线法,分析了不同拓扑风电汇集系统下的电压稳定性,计算出了电压稳定裕度,但是该文献没有对海上风电汇集系统的设计经济性进行分析。文献[7]从风电场尾流效应的角度对风电场的规划进行了优化,但是没考虑风电场内风机的电缆排布造成的不同拓扑对风电场规划经济性的影响。
通过对海上风电场汇集系统的组成和特征以及汇集系统的经济性组成因素进行分析,以投资成本最低为目标,建立汇集系统经济性数学模型。在此模型基础上,提出了一种经济性优化组合算法。首先,对汇集系统中的风机排布采用放射型模糊聚类算法(radial fuzzyC-means,RFCM)进行模糊聚类分片,然后将聚类片区得出的海上风电机群的海底电缆线路分布路径采用图论的Prim最小生成树算法进行优化找出电缆连接最小路径,得出最经济性的分布拓扑,通过此算法可以解决利用穷举法优化海底电缆拓扑时遇到的多维数问题,为大型海上风电场的汇集系统经济性优化提供了一个简便快速的方法。最后对山东半岛北风电场实例进行该组合优化算法的算例分析,证明该组合优化算法的有效性。
1 风电场经济性影响因素量化建模
海上风电场汇集系统主要由机组部分、开关部分、海底电缆线路部分以及换流站组成[8]。相较于地理位置决定的机组开关以及换流站部分,每台风机之间的电缆连接线路更为灵活,不同的连接拓扑将对全局成本造成较大的影响,因此具有较大的优化空间。同时,经济性分析需要考虑不同因素的影响,其中投资成本与各个不同的因素有着直接或间接的约束与联系。以海上风电场电气接线汇集系统全局总投资最小为目标函数,建立经济性数学模型。
首先,建立总投资成本目标函数:
minC1,Seach≤SB
(1)
式(1)中:C1为海上风电电气汇集系统总投资最小成本;Seach为功率约束条件每条线路实际传输的功率;SB为每条线路传输的额定功率。
海上风电内部集电系统的经济性主要由投资成本、维护成本以及损耗费用几项成本组成相互影响。
投资成本主要组成为
E=E1+E2+E3
(2)
式(2)中:E1=f1N,为风机以及风机侧变压器的投资成本,f1为单价,由风电场汇集系统的电压等级决定,N为风机数量;E2=Bi+Si,为海上变电站投资成本,包括换流器成本Bi以及其他费用Si;E3=Ce1+Ce2,Ce1为海底电缆总成本,是单位长度、总段数以及电缆总长度的乘积,Ce2为海底电缆敷设成本。
维护成本可根据统计规律,按照直流输电系统的维护成本占总投资成本的0.5%计算[9]。
损耗费用主要包括换流站损耗和线路损耗。换流站损耗通常由换流站损耗率给出,对于换流站损耗率,有文献对其进行过研究,根据相关文献,取换流站损耗率为1.75%,线路损耗为

(3)
式(3)中:P为线路输送总功率;UDC为直流电压输送等级;R为单位直流电阻,取0.036 6 Ω/km;L为线路长度[10]。
在经济性模型中,海上风电汇集系统的经济性由各成本因素组成,每个因素直接相互影响制衡,接下来从经济性优化更灵活的海底电缆线路排布角度出发,以投资成本最优为目标对海上风电汇集系统进行优化分析。
2 经济性优化算法
2.1 经济性优化思想设计
从第1节的分析可以看出,海上风电汇集系统的经济性各项因素相互关联、相互制约,优化经济性的可实现组合空间很多。根据海上风电场的特点和约束条件,设计了一种算法,可以较好地解决经济性优化的问题。该算法的主要流程如下。
(1)选择一个大型分区的海上风电场的典型海上风电场,采用RFCM算法对该典型风电场进行变电区域内的风机分片,考虑的条件包括海上换流站的位置、换流站容量以及风机之间的距离等。
(2)对每个分区分串后的风机找寻最优电缆拓扑链接路径,这一步可以用图论法和最小生成树Prim算法完成,假设风机为一个点,各电缆连接就是点点之间的线段相连的方法,即图生成树。此步考虑的条件包括风机间的距离、电缆额定容量等。
(3)根据所分片区和风机串的种类计算所有分法下的最优汇集拓扑总成本,寻求最优成本,算法结束。
2.2 单个汇集区域内风机群分组(片)算法
2.2.1 模糊C聚类算法
模糊C聚类算法(fuzzyC-means,FCM)算法是一种基于模糊的划分方法,不同于硬聚类严格的把对象划分为不同的簇,FCM算法抛开非此即彼的一种柔性划分方式,柔性划分的优化目标能使得同一簇对象相似程度最高,不同簇对象相似程度低。对样本采用与不同类别之间建立了非1与0的不确定描述,对事物的分类更加的客观[11]。
FCM算法不同于硬性聚类,而是定义了一个μA(x)的隶属度函数矩阵,隶属度自变量的范围为某集合空间内的所有点,对于一个对象x在某集合中的隶属度大小的值即为其属于某集合程度的函数,取值为0~1。通过判断隶属度函数的值可以判断某对象属于该集合的程度,例如某对象x的μA(x)的值为1时,相当于硬性聚类集合中的x完全隶属于某集合,一个定义在空间X={x}上的隶属度函数即为定义在论域X={x}上的模糊子集。对于空间内有限个对象x1,x2,…,xn模糊集合A可以表示为
A={(μA(x),Xi)|Xi∈X}
(4)
有了模糊集合概念的定义,就将样本空间内所有元素属于某个集合柔性划分了,通过一个隶属度函数矩阵来判断它们的从属关系,用一个模糊集合来定义每类聚类的集合簇,此时,每个样本空间内的样本点隶属于某个簇的隶属度的值一定会在区间[0,1]。
对于分类数目是由聚类中心参数C决定的,另外参数m也是FCM算法的重要参数。聚类中心的数目不能是空集即C>1,同时应该保证远小于样本的总对象数目。参数m控制算法的柔性程度,不宜过大或者过小,一般取值为2。
最终输出的隶属度矩阵为一个C×N的模糊划分矩阵,表示空间内的每个样本对象与空间内每一类聚类中心C的隶属度大小。聚类中心可表示出每个类别代表点的平均特征,因此通过该矩阵的值,按照模糊集合中的最大隶属度原则就可以判断出样本归于哪一类,确定其模糊分类。
FCM算法把n个向量xi(i=1,2,…,n)分为C个模糊组,计算出每个模糊组的聚类中心,使得相似程度高的价值函数达到最大,与模糊划分的规则相结合,隶属矩阵μA(x)允许隶属度取值在[0,1],总和不能超过1,需遵循归一化原则,即
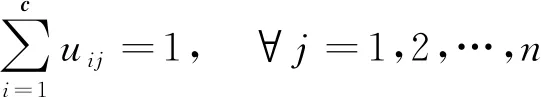
(5)
FCM的目标函数为
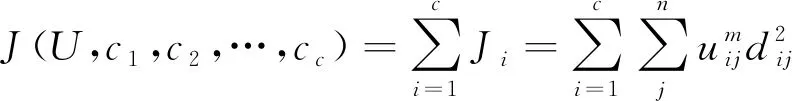
(6)
式(6)中:隶属度矩阵uij介于0~1;模糊N簇的聚类中心为ci;dij为第N簇聚类中心与空间中第j个对象间的欧几里得距离,即为‖ci-xj‖。
聚类中心ci的计算公式为
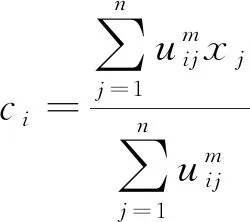
(7)
隶属度迭代公式为
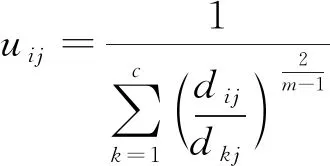
(8)
用FCM方式对风机进行分串的步骤如下:
步骤1定义各参数数值,包括聚类簇数C,模糊系数m,迭代次数限制N,误差范围ε;读入每台风机坐标f(x,y),初始化隶属度矩阵U,满足归一化条件。
步骤2求出聚类每个中心c的值ci(i=1,2,…,c)。
步骤3计算目标函数。当其值或改变值小于所设定的阈值时算法停止。
步骤4计算新的U矩阵。返回步骤2。
每次迭代判断群心O有没有发生变化用一个矩阵范数比较c(k)与c(k+1),若范数小于设定误差,即‖c(k+1)-c(k)‖≤ε时停止迭代,输出结果,否则进行下一次迭代[12]。
2.2.2 放射型模糊聚类算法风机群分片
如用FCM对一个区域风电场内的风机进行分片,每个片区都存在一个聚类中心点,即海上换流站。但是每台风机均要与海上换流站有连接的通路,且不经过其他的片区,所以在一个风电场只布置一个换流站的情况下,采用传统的FCM分类如图1会造成电缆连接路径复杂交叉。理想的分片方式是以风机接入点换流站为中心,呈放射性分布,如图2所示。

图1 块状聚类Fig.1 Block clustering

图2 放射状聚类Fig.2 Radial clustering
所以为了得到放射状聚类分布,对传统的FCM算法进行改进得到放射型模糊聚类(radial fuzzy C-means,RFCM)算法,主要区别在于①确定了分片内风机接入点即海上换流站的地理位置坐标,输入算法时将其位置信息输入,但该坐标不参与聚类过程;②更新模糊分类矩阵时,考虑的不再是风机和聚类中心的距离而是与各聚类群心c到海上换流站连线的距离,其余过程相同。

图3 放射型模糊聚类算法RFCM 求dij解示意图Fig.3 Schematic diagram of radiative fuzzy clustering algorithm RFCM for dij solution
2.2.3 风机群拓扑寻优汇集接入算法
图的最小生成树是指一棵连接图中所有顶点,具有权重最小的树,树的权重为所有树边的权重之和。最小生成树可以应用在电路规划中,规划出既能连接各个节点又能使材料最为节省的布局。计算最小生成树有两个经典算法,分别是Kruscal算法和Prim算法。下面介绍Prim算法的原理以及实现。Prim算法是以贪心算法为基本原理,其思路是从某一顶点出发,判断与其相邻的点所连的边的距离,在生成树中加入距离最短即权重最小的边。同理,从当前生成树中的所有种子的顶点出发,选择最小权重相邻边加入其中,以此类推,从而得到最小生成树[13]。
对于海上风电场风机间的电缆通路,可用Prim算法寻求最优拓扑来使经济性达到最优。具体实现方法如图4所示,最后得出的绿色路径即为最优经济的电缆拓扑。
3 算例分析
3.1 山东海上风电场规划布局
山东省海上风电基地规划分为三个部分:渤海海上风电基地、半岛北海上风电基地、以及半岛南海上风电基地。其中,半岛北海上风电基地面积 1 082 km2,离岸距离30~68 km,离岸距离最远适合使用柔性直流汇集输送,如图5所示。
根据半岛北海上风电基地位置图可知,风电场BDB7#离岸平均距离为38 km,BDB3#、BDB5#、BDB6#离岸平均距离为45 km,BDB1#、BDB2#、BDB4#、BDB9#离岸平均距离为55 km, BDB8#离岸平均距离为64 km[14]。根据相关信息以及条件,设计3个岸上开关站。该风电场的位置信息如表1所示。
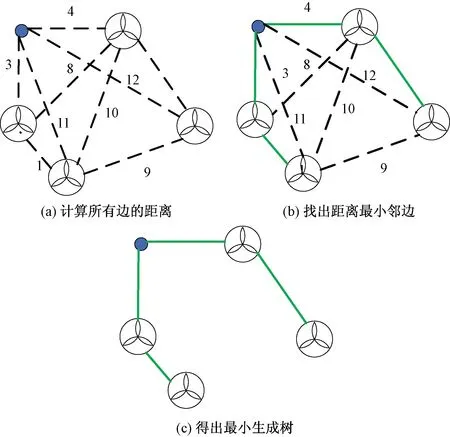
图4 Prim算法求解最小生成树图示Fig.4 Diagram of Prim algorithm solving minimum spanning tree
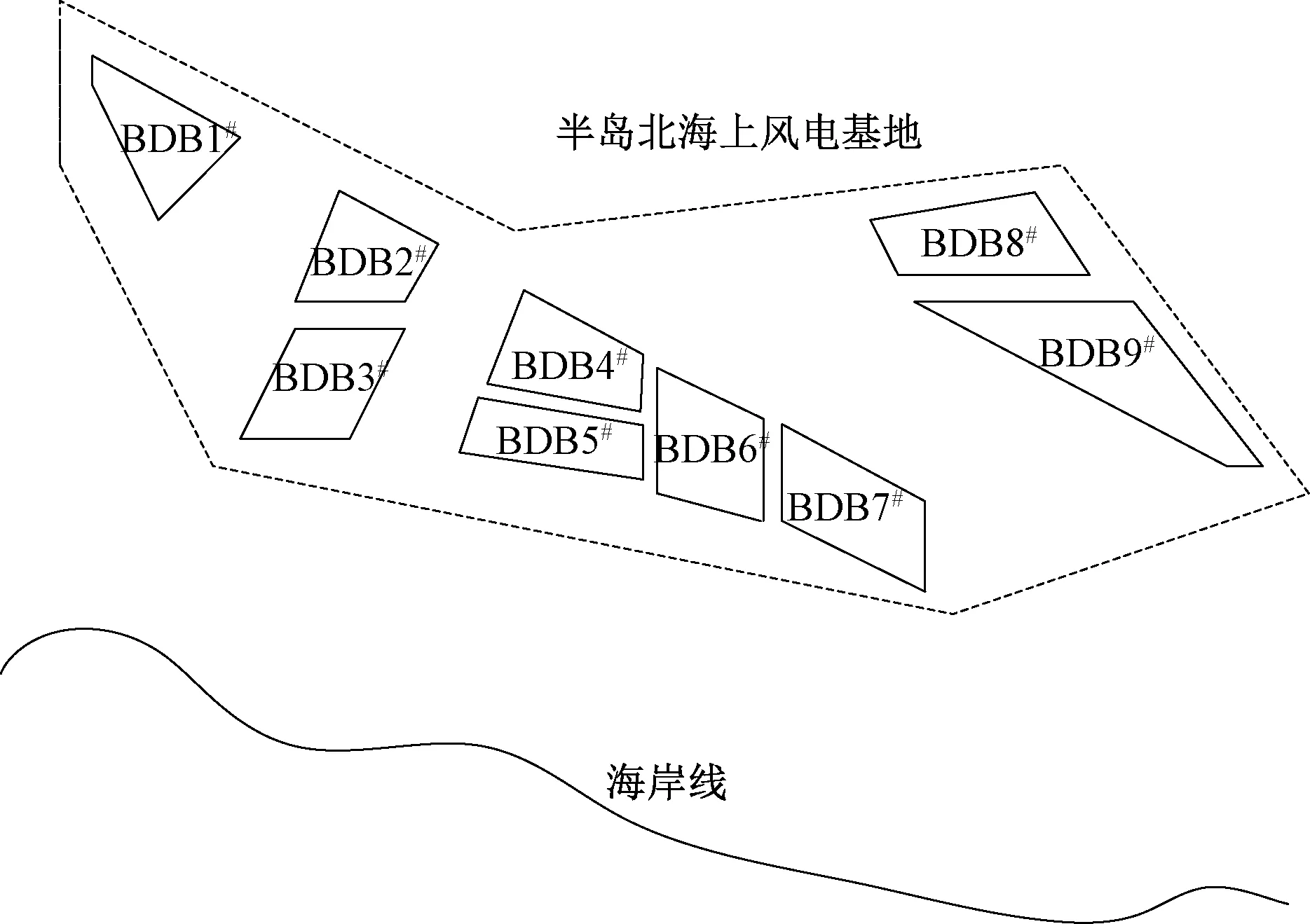
图5 半岛北海上风电基地位置图Fig.5 Location of north sea wind power base on the peninsula

表1 半岛北海上风电风电场位置信息
图6所示为设计的点对点拓扑结构,该结构为多端柔性直流汇集拓扑,根据半岛北海风电基地的各个风电场的地理位置以及传输距离,将BDB1#、BDB2#和BDB3#的功率汇聚到开关站1,将BDB4#、BDB5#、BDB6#和BDB7#的功率汇聚到开关站2,BDB8#和BDB9#的功率汇聚到开关站3。

图6 海上风电场交流汇聚柔直点对点传输拓扑Fig.6 Point to point transmission topology of VSC-HVDC system with offshore wind farms
因为山东半岛北海上风电基地离岸较远,所以适合采用高压柔性直流输送,图6拓扑是根据山东半岛北海上风电场的排布设计的九个区域风电场接入岸上的拓扑,其中,对外来看,每个片区有不等的风机群能量汇集进入海上换流站从而送到岸上换流站并网,对内即为其能量汇集系统的设计。
表2为半岛北海上风电场综合信息,根据北岛海上风电场的相关信息,选取其中一个典型风电场BDB6#来对其电气汇集系统进行所设计的经济性优化组合算法的算例分析。
3.2 优化过程
按照2.1节的优化算法对半岛北海上风电场中的典型风电场进行优化,该风电场有80台风机。优化过程所需成本参数如表3所示。
运用MATLAB进行优化算法分析得出风机位置图。下面简述优化过程。

表2 半岛北海上风电风电场综合信息

表3 海上风电集电系统所需成本
3.2.1 进行变电区域内的风机分片
采用RFCM模糊聚类方法对风电场进行分片,将BDB6#区海上风电场的风机分6片和3片,对比不同方案的优化结果。如图7所示,在MATLAB中得出的风机距离片区图,再导出数据运用Origin标出海上换流站的位置以及分片区的范围。
图7(a)所示为将图5中的BDB6#海上风电场区域内的风机进行RFCM算法的分6片区的聚类结果,可以看出以海上换流站为中心,6片区风机呈放射状分布在海上换流站的周围,为之后Prim最小生成树寻优做准备。
图7(b)所示为将图5中的BDB6#海上风电场区域内的风机进行RFCM算法的分三片区的聚类结果,可以看出以海上换流站为中心,三片区风机呈放射状分布在海上换流站的周围。

图7 RFCM算法区内风机分片结果Fig.7 Results of fans in RFCM algorithm region
3.2.2 寻找最优电缆拓扑链接路径
选取分片后的风机,采用Prim最小生成树算法对其进行电缆拓扑最优路径计算,分别得出分3串与6串时的电缆连接拓扑结构,并且列出海底电缆分6串时的每一区最小路径计算的结果。
图8所示为分六区时每个小分区的风机串的最优电缆拓扑路径,综合每个片区的最优电缆拓扑路径得到如图9(a)所示总的最优路径规划图。
图9所示为分3串与6串的整体优化结果。
3.2.3 优化结果
优化结果如表4所示。可以看出分片数3的总投资要小于分片数6的总投资。相较于穷举法,本算法更具有参考依据,并且通过本算法大大缩短了计算时间,对解决海上风电场汇集系统优化更具有针对性,且优化过程更具有可操作性。
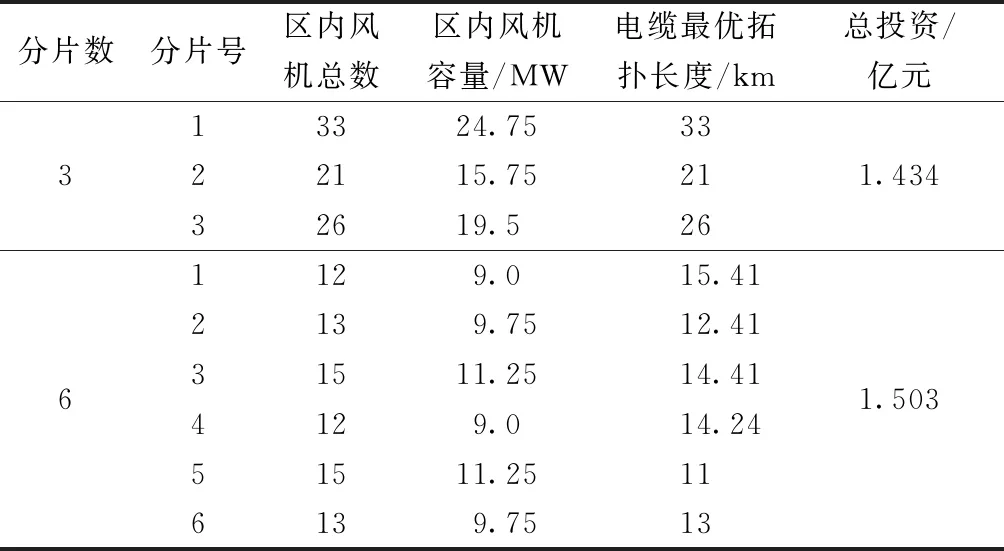
表4 BDB6#海上风电场分区优化结果
4 结论
详细介绍了大型海上风电场电气汇集系统经济性优化的解决方案,设计了一种自上而下的组合优化算法,对大规模的优化问题进行了多次降阶,一是将海上风电场的内部风机群分片,二是将分片后的风机群分串,此组合算法解决了穷举法优化拓扑结构的维数灾问题,为简洁快速地解决大型海上风电场汇集系统经济性优化问题提供了一种方法。具体解决方法如下。
(1)选择一个大型分区的海上风电场的典型海上风电场,采用RFCM算法对该典型风电场进行变电区域内的风机分串,考虑的条件包括海上换流站的位置、换流站容量以及风机之间的距离等。
(2)对每个分区分串后的风机找寻最优电缆拓扑链接路径,这一步可以用图论法和最小生成树Prim算法完成,假设风机为一个点,各电缆连接就是点点之间的线段相连的方法,即图生成树。此步考虑的条件包括风机件的距离、电缆额定容量等。
(3)根据所分区域和风机串的种类计算所有分法下的最优汇集拓扑总成本,寻求最优成本,算法结束。
通过分析山东电网的规划风电场,给出实际算例的计算优化对比,论证了大型海上风电场汇集系统经济性优化方法是快速有效的,为实际的海上风电场规划问题提供了一种科学的定量的规划思路和评估手段,对实际工程实施具有很强的指导意义。
