基于非参数估计的无功电压控制响应规则辨识

周艳平 雷昊 辛平安 杨显睿 李滢洁

（云南电网有限责任公司昆明供电局 云南省昆明市 650000）

1 非参数估计

Wolfowitz 在1942 年引入了“非参数”术语，它涵盖了一组统计技术，用于未指定所要处理的随机变量分布的函数形式的情况。在其早期形式中，这主要包括使用秩统计的方法，并且也被称为“无分布”方法。大多数情况下，这些方法都用于执行假设检验。这种类型的非参数方法的优点是可以应用于序数和秩数据。数据可以是频率或计数，而不必连续测量。

在基于非参数估计的无功电压控制响应规则辨识中，数据模型不是先验指定的，而是根据数据确定的某种形式。在这种非参数模型中，存在估计参数，甚至在大多数情况下甚至还有许多参数，因此，这种估计方法的主要示例是核估计器，样条和小波估计器。这些技术也称为“平滑方法”。通过选择最大的系数而不是预定的子集，可以很好地捕获奇点。因此，将最小系数设置为零，可消除大部分噪声，而不会过多地影响无噪声数据。使用此阈值或任何复杂的变体（总是非线性处理），总是使用小波分解的主要原因，并且总是与数据的间歇性相关联，即在其他情况下平滑行为中存在孤立的奇异点。阈值的使用取决于小波表示的稀疏性。另一方面，多尺度属性通常用于其他跨尺度处理，例如，在阈值化后消除误差，或通过跨尺度查看以纠正误差。

2 电压无功综合控制

电压无功综合控制策略在一定程度上减少了无功功率在电网中的远距离传输，优化了变电站负荷端的电压。在实际运行中，与变电站相邻的节点电压似乎有所提高。电场应配备无功功率控制系统，以参与系统无功功率调节和电压控制。电场会自动调节其无功功率，以控制公共耦合点（PCC）处的电压。调节率和控制精度也应满足电力系统电压调节的要求。当电网电压在正常范围内时，电场应能够将PCC 的电压控制在额定电压的97-107%的范围内。同时，该要求规定了不同的无功功率控制类型，即电压控制模式，无功功率控制模式和功率因数控制模式，将简要说明如下：电压控制模式；管理电场中的无功功率，从而可以实现系统操作员给定的连接点处的电压目标。无功功率控制模式；无功功率控制系统根据系统操作员给出的无功功率控制目标进行操作。功率因数控制模式；无功功率控制系统根据系统操作员给出的功率因数控制目标进行操作。

为了避免电力系统建模带来的误差，提出了一种基于多场景电压无功相关分析方法。该方法利用历史数据训练获得具有代表性的负荷情景，明确工作调节措施与节点电压的相关性表达式，根据得到的函数关系进行电压估计，根据估计效果确定对节点电压影响较大的因素。最后，得到了电压与无功功率相关的有效信息和结论。

3 基于非参数估计的无功电压控制响应

从系统安全和能量损耗的角度来看，最优无功功率分配（ORPD）对于电力公司来说是一个重要问题。ORPD 是最优潮流（OPF）问题的一种特殊形式，其中，通过调节发电机电压设定点，弱母线中的无功功率补偿以及变压器的最优设置，可以优化各种目标函数，例如传输损耗或电压稳定性增强指标分接比。

3.1 样本预处理

考虑到电力系统中负载需求的随机性，需要对电力系统的运行和规划中的负载不确定性进行建模。通常，可以使用正态或高斯PDF 对负载不确定性进行建模。据推测，所述负载PDF 的平均值和标准偏差，μd和σd是已知的。第d 个负载方案的概率由（需求方案的概率d）表示。

3.2 计算函数分析

电力系统的电压稳定性与无功功率管理密切相关。因此，将电压稳定性的提高与总有功功率损耗和电压偏差一起视为另一个目标函数。ORPD 问题变量的子集可以描述如下。

ORPD 问题的第二个目标是在负载总线上维持适当的电压水平。电气设备的构造可优化额定电压。违反此额定电压会导致电气设备的效率降低和寿命缩短。因此，可以通过最小化负载总线上与相应额定值的总电压偏差（VD）来优化系统的电压曲线。该目标函数表示如下。

可以使用一些方法来关联ORPD 问题中的静态电压稳定性增强。例如，将电源电压曲线用作静态电压稳定性建模的指标。使用基于模态分析的静态电压稳定指数来确定电压稳定裕度。雅可宾矩阵的最小奇异值和最小L-指数是用于确定系统电压稳定裕度的其他指数。选择指数以量化电压稳定性，该指数说明了电力系统当前状态到电压稳定极限点的距离，可以使用潮流解决方案对其进行评估。应当指出，L-index 的值在0 到1 之间变化。L-index 值小于1（电压崩溃点）并接近0（空载点）对应于更大的电压稳定性裕量。网络总线的电压幅度和相角是系统负载和发电量的函数。通过增大发射功率并在最大功率传输位置附近，负载总线的电压稳定性指标值变得更接近1，这表明系统更接近电压崩溃。

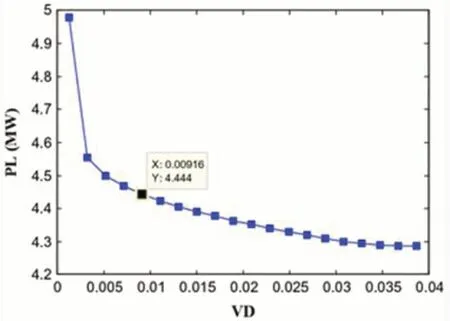
图1：无WF 的DMO-ORPD 的帕累托最优阵线

3.3 基于Group-Lasso的非参数估计

Tibshirani 于1996 年提出的Lasso(Least Absolute Shrinkageand Selection Operator)算法是一种基于L1 范数的多元线性回归方法，它能够很好地解决电力数据样本中存在的多重共线性问题，同时能够防止模型对于训练集的过拟合，使其对测试具有较好的泛化能力。

选择合适的阈值一直是研究的主要领域，包括通用阈值（Donoho 和Johnstone1994）或虚假发现率阈值（Benjamini 和Hochbery1995）。另一类阈值集中在结果的预期，综合平方损失（即险）上。斯坦因的无偏险估计器和修改（例如交叉验证）提供了寻找最小险阈值的实用方法。第三，和广泛类的阈值评估方法是基于贝叶斯-大多是经验贝叶斯-模型。先前的无噪声系数模型反映了稀疏性的思想，主要是通过零膨胀或其他带有重尾的混合模型。

4 算法分析与仿真

在IEEE30 总线测试系统上进行仿真。为了证明所提出方法的有效性，研究了以下几种情况。

（1）在没有电场的情况下进行确定性优化（通过忽略负荷和电场的不确定性）。

（2）通过电场发电量的预期值和负荷平均值的确定性优化（忽略不确定性）。

（3）带有负荷和电场发电不确定性的随机优化（使用基于方案的方法表示不确定性）。

IEEE30 总线系统包括30 条总线和6 条发电机总线。总线1 是松弛总线，总线2、5、8、11 和13 是PV 总线，而其余24 总线是PQ 总线。该网络由41 个分支机构，4 个变压器和9 个电容器组组成。负载分接变换变压器下有四个分支6-9、6-10、4-12 和28-27。抽头比率在区间[0.9，1.1]之内。另外，选择总线10、12、15、17、20、21、23、24 和29 作为并联VAR 补偿总线。

IEEE30 总线测试系统可达到帕累托前沿，而无需考虑任何不确定性，并且无需集成能。为了与先前文献中发表的作品进行比较，VAR 补偿设备由连续变量建模。通过使用最小-最大模糊满足标准，最佳折中解决方案是Solution#16，最大弱隶属度函数为0.7734。相应的PL 和VD 分别等于4.4438MW 和0.0092。还值得注意的是解决方案#1 对应于解决方案#1 中的损耗最小化情况，仅PL 被最小化，而PL 的最小值为4.2875MW。

为了通过ε 约束方法解决多目标ORPD 问题，有功损耗的最大值和最小值（F1）和电压偏差（F2）考虑分别等于3.8771MW，3.1651MW，0.0428pu 和0.0012pu。通过分别最大化和最小化MOORPD 的目标函数来达到这些极值。这意味着在解决方案#1 和#20中，目标分别是使PL 和VD 最小化。在这些最佳解决方案中，解决方案#16 最大限度地降低了两个目标，即PL 等于3.2983MW，VD 为0.0099。

总结了案例I 和案例II 的有或没有WF 和SMO-ORPD 的DMO-ORPD 的结果。根很明显，通过在系统上安装电场，可以显着减少实际功率损耗（确定性模型中的PL 和随机模型中的EPL）。还可以看出，在SMO-ORPD 的情况下，预期的EPL 高于DMO-ORPD 的情况。此外，描绘了获得的VD 和EVD 值在案例一和案例二中。从该图可以明显看出，电场的安装会导致电压偏差的恶化，特别是在SMO-OPRD 的情况下。这主要是由于在不同情况下电场输出功率的波动。由于位置上与基函数相对应的系数很大，因为它们承担构成奇点的作用。因此，通过选择最大的系数而不是预定的子集，可以很好地捕获奇点。因此，将最小系数设置为零，可消除大部分噪声，而不会过多地影响无噪声数据。使用此阈值或任何复杂的变体（总是非线性处理），总是使用小波分解的主要原因，并且总是与数据的间歇性相关联，即在其他情况下平滑行为中存在孤立的奇异点。阈值的使用取决于小波表示的稀疏性。另一方面，多尺度属性通常用于其他跨尺度处理，例如，在阈值化后消除误报（用于奇点之间的更平滑间隔），或通过跨尺度查看以纠正误报（用于更清晰地重构奇点）。

考虑了系统负荷和力发电的不确定性，研究了力发电系统中的随机多目标最优无功功率分配（SMO-ORPD）问题。为了在上述不确定性条件下进行决策，采用了两阶段随机优化模型。在多目标优化框架中，同时优化了实际功率损耗，电压偏差和电压稳定性改善指标（L-index）。利用ε 约束方法解决了多目标优化问题。将确定性情况下的结果与最近应用的基于智能搜索的算法进行比较，发现在这种情况下，所提出的方法可以为两个目标函数找到更好的解决方案。在随机情况下，将获得一组全面的决策变量，包括此处，现在和观望控制变量。所提供的SMO-ORPD 模型已使用IEEE30 总线测试系统进行了验证。数值结果证实，与确定性情况相比，在存在力发电的情况下，有功功率损耗的期望值和L 指数降低了。这证实了力发电对减少系统损耗的积极影响。