基于概率矩阵分解的组推荐系统研究

宋玉龙 马文明 刘彤彤

（烟台大学 山东省烟台市 264005）

1 引言

近些年，互联网技术的不断发展，让人们可以很容易地获取大量的各种信息。随之造成的是信息爆炸与过载，这让我们很难从海量的信息里面获取自己真正想得到的部分。为了缓解这些窘况，推荐系统通过对海量数据的分析，为用户选择合适的推荐物品，提供个性化的推荐结果，此类方法通常可以满足许多用户的推荐需求。又由于实际生活中存在大量由多个用户组成的群组参与的活动（如健身房给锻炼的用户进行的音乐广播或给一个家庭推荐一部电影），这些活动往往更偏向一个权威的人或者算法对群组进行指导，这就需要面向群组的个性化推荐，组推荐系统于是应运而生。

2 相关工作

组推荐系统的面向受众是由多个用户组成的一个个群组，与传统推荐相比会考虑到更多的影响因素，其中一个关键部分是对群组中的成员融合策略。融合策略通常可以分为用户偏好融合和推荐结果融合。用户偏好融合是指将组内用户的偏好模型融合成为一个群组模型，根据结果模型获得群组对物品的评分或者推荐列表。推荐结果融合是指给组内所有成员分别进行推荐，将他们的推荐评分或者列表进行合并，获得该组对物品的推荐结果。

2.1 偏好融合策略

表1 列举了组推荐系统中常见的5 种评分融合策略。其中较为常用的是平均值策略和最小痛苦策略。

2.2 概率矩阵分解

Salakhutdinov R 在零八年提出概率矩阵分解算法（Probabilistic Matrix Factorization），是近些年比较流行的推荐算法。假设有N个用户和M 个物品，对应的评分可以形成一个M×N 矩阵R，Rij表示用户i 对物品j 的评分。通常R 非常稀疏，只有很少的元素是已知的，而我们要估计出缺失元素的值。

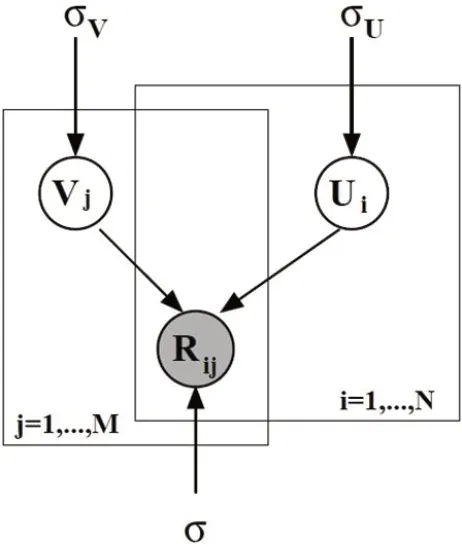
图1：PMF 的概率模型图

传统矩阵分解将矩阵RM×N分解为两个维度更低的矩阵的乘积其中K 表示潜在向量的维度。通过不断学习迭代来使逼近评分矩阵RM×N，同时也将得到未评分项目的预测评分。

概率矩阵分解假设由用户偏好向量和物品潜在向量的内积来决定评分矩阵R，且评分服从高斯分布，即：

其中N 表示高斯分布。概率模型图如图1 所示。

则观察到的评分矩阵的条件概率为：

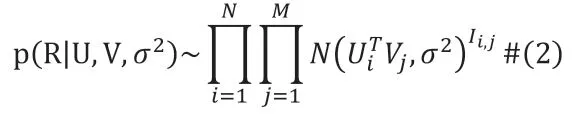
表1：组推荐系统常见融合策略

图2：基于概率矩阵分解的群组推荐方法框架

Ii,j为指示函数，如果用户i 已对物品j 进行了评分，则为1，否则为0。

再假设用户潜在特征向量和物品的潜在特征向量都服从均值为0 的高斯先验分布，即：

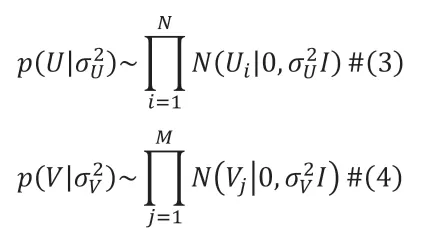
其中的I 不是指示函数，表示一个对角阵。

然后计算U 和V 的后验概率为：

两边取对数得到：

其中K 是潜在变量的维度，C 是无关常数。

于是我们可以通过最小化以下目标函数来最大化后验概率：

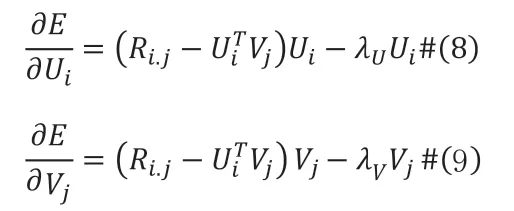
然后用随机梯度下降法（SGD）更新Ui和Vj：

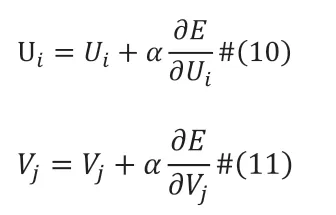
直到收敛或到达最大迭代次数。

3 群组推荐系统设计

本文提出的方法框架如图2 所示。

根据图2 可以看出，本文所用框架主要包括以下步骤：

获取用户-项目评分矩阵，进行概率矩阵分解，得到用户对未评分项目的预测评分。

（2）将用户的预测评分用恰当的融合策略进行融合，获得该群组的评分。根据评分生成给该群组的推荐列表。

以上，基于概率矩阵分解的组推荐系统，输入数据为每个用户的评分，输出每个群组的推荐列表。

4 结束语

随着以多个用户组成的群体为单位的活动不断增多，传统推荐方兴未艾，渐渐渗入到千家万户，成为日常生活中不可缺少的一部分。群组推荐也开始逐渐得到越来越多的关注，给我们带来了更多的机遇和挑战。

传统的协同过滤方法能够共用大众经验过滤机器难以识别的信息，但在面对体积过大的数据量与评分太稀疏的矩阵时都显得有心无力。而概率矩阵分解算法在大型、稀疏、不平衡的数据集上都有很不错的表现，能够提高个性化推荐的效率。我们未来可以尝试在概率矩阵分解中融入用户间的社交信息，期望进一步提高系统性能。