一种新的增广路径最大流算法

李江龙 马诗贵

（遵义医科大学计算机网络管理中心 贵州省遵义市 563000）

1 引言

“网络流理论”是在20 世纪50 年代由Ford-Fulkerson 两人建立的，是网络应用的重要组成部分，1955 年，最大流问题在铁路运输行业被首次提出，在1956 年，Ford-Fulkerson 又创建了最大流理论，首次提出了“最大流，最小割”的重要学说，给出了解决最大流问题的算法。

目前，最大流算法分成两大类，第一类是增广路径算法，包含Ford-Fulkerson 算法[1]，Edmond-Karp[2]算法以及Dinic[3]算法等；第二类是预流推进算法，典型的有FIFO 预流推进算法和HLLP 算法等。

本文主要研究增广路径算法的改进方法。在增广路径算法中，由于算法本身的缺陷，导致对于路径的选择存在随机性，加上我们采用了贪婪算法求解最大流，所以在开始寻找增广路径时并没有考虑到全局最优选择，即便采用了最优选择，在某些特定的情况下，仍然会造成在找到正确的最大流之前，网络图提前失去连通性，这是一个影响算法正确性的致命问题。为了解决问题，我们必须牺牲算法的效率，寻找通用性较高的方法，保障算法的正确性。以往的最大流算法利用反向边思路提供一个反悔机制[4]，通过将错误占用的边以及流量退还，给算法一个重新选择路径的机会，选出不会导致网络图提前失去连通性的增广路径，这种方法能很好的解决上述问题，但是另一方面，算法的复杂度也由于反悔带来的多余步骤而上升。本文提出一种新的增广路径最大流算法，关键顶点可行分量算法（KPFC），引入关键顶点机制，将其去除，从而求出网络图的可行分量，再在可行分量中寻找增广路，从而简化路径寻找的难度，替代反向边机制，有效降低算法复杂度。

2 基本概念

2.1 （容量）网络[5]

在有向连通图D=(V,E)中，记（容量）网络为G=(V,E,c)，需满足：

（1）在D 中存在特定的两个顶点，分别为源点与汇点；对于D 中的中间节点必须是同时具有入弧和出弧的节点。

2.2 流量、容量和可行流[5]

流量是指链路上正在流过的数据量，通常用f(u,v)来表示，u,v是两个顶点的编号，流量可以是管道中的水量，也可以是道路中的车流量等；容量是指链路的最大承载量，通常用c(u,v)来表示；可行流是指满足条件的流量。

2.3 增广路径[5]

增广路径是指连通源点和汇点的一条路径，这条路径上的所有正向边都满足反向边满足这样的路径叫做增广路径。

2.4 残存网络[5]

图1：KPFC 算法流程图

2.5 距离标号和允许弧[5]

2.6 最大流问题的数学模型[5]

那么fst成为容量网络G 的全部可行流的其中之一，若此流的值为全部可行流中的最大值，则此流叫做最大流，记为fmax。在上式中符合条件的弧叫做饱和弧，符合条件的弧叫做非饱和弧。可行流符合流守恒定律，表现在源点S 流出的全部流量都能够通向汇点T 并且被全部接收；除了源点S 与汇点T，全部的中间节点都只起到流通流量的作用。

3 算法描述

3.1 算法步骤

（1）根据原网络图创建结构体数组。

（2）找出并记录关键顶点，构建可行分量。

（3）利用DFS 算法在可行分量中寻找增广路径。

（4）若可行分量仍然连通，返回步骤（3），若可行分量不连通，删除无用顶点（若存在），判断是否存在关键顶点，若存在，加入关键顶点，返回步骤（2）；若不存在，则算法结束。

KPFC 算法的流程图如图1 所示。

3.2 算法分析

关键顶点可行分量算法，又称KPFC 算法，该算法的改进在于取消了反向边机制，属于增广路径算法，利用一维结构体数组来存储网络图，引入关键顶点来构建网络图的可行分量，解决路径选择不合理等相关问题。所谓关键顶点，即去除之后在保障图的连通性的前提下，能够最大限度的将原图简化的顶点，关键顶点的确定满足以下几个条件之一：第一，入弧和出弧数量之和大于2；第二，入弧或出弧数量小于1；第三，邻接点数量小于2。 在判定一个满足上述条件的顶点为关键顶点之前，需对去除此顶点后，是否会使网络图失去连通性做出判断，若不影响图的连通性，才将顶点判定为关键顶点，在网络图中，若存在多条增广路径，那么这些路必定会经过关键顶点一次或多次，关键顶点不止一个，在将所有关键顶点都去掉之后，我们能够得到一张最简化的连通图，这个图便称为原网络图的一个可行分量。 在寻找增广路径时，如果发现图不再连通，判断可行分量中的顶点是否还有剩余容量不为零的入弧和出弧，若一个顶点的所有入弧或出弧的剩余容量为零，便将此顶点判定为无用顶点，可将其删除，后续计算无需再考虑此顶点。再加入拥有最多邻接点的关键顶点，优先消耗此类（邻接点最多）顶点的弧的剩余容量，可以快速的减小原网络图的复杂程度，加入关键顶点后，继续寻找新的关键顶点，可以形成新的可行分量，进而寻找增广路径，这样重复执行，直到所有关键顶点都被加入，就能找出最大流。

3.3 算法实例分析

有图如图2 所示，求其最大流：

将图2 用一维结构体数组方式表示为：

本算法采用邻接矩阵来表示图，在具体代码里，用一个结构体一维数组来体现，假设图包含n 个顶点，数组的元素数量即为n 个，每一个元素都是一个结构体，表示一个顶点，其中包含四个参数，分别表示顶点的父顶点，子顶点，入弧容量和出弧容量，每一个参数都是一个一维数组，因为一个顶点可能存在多个父顶点或子顶点。如上所示，从上到下分别为S、A、B、C、D、T 顶点的满足条件的邻接点和弧的容量，由于S 顶点没有父顶点，所以其参数用-1 来表示，T 顶点的参数同理，图中有两个关键顶点，分别为A 和C，关键顶点用一个一维数组kpoint 来表示，此时，kpoint={A,C}，在去掉这两个关键顶点之后，原图变成如下所示：

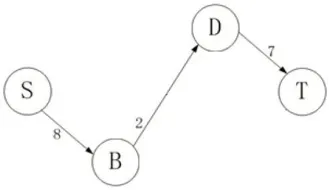
这是一个可行分量，只能找到一条增广路径，就是S-B-D-T，当前流量为路径上的最小容量，即为2，设最大流为SUM，当前最大流SUM=2。

此时找不到增广路径，我们在图中加入拥有最多邻接点的关键顶点A（顶点A 和C 的邻接点数量一样，按照顺序添加），此时kpoint={C}，图变为如下所示：

此时可以找到新的关键顶点B，加入到kpoint 数组，kpoint= {C,B}，构建新的可行分量，如下所示：

找到一条增广路径，即为S-A-D-T，当前路径流量为4，所以SUM=2+4=6。

此时A 点所有入弧容量为零，判定为无用顶点，直接删除，找不到新的增广路径，加入关键顶点C，图变成如下所示：

图不连通，查看是否还有关键顶点，存在关键顶点B，将其加入图变成如下所示：

此时可以找出一个关键顶点D，去除后，图变成如下所示：

找到一条增广路径为：S-B-C-T，当前路径可行流为2，最大流SUM=6+2=8。

图失去连通性，加入最后一个关键顶点D，图变为如下所示：

到此，网络图不再连通，并且不存在关键顶点，算法结束，最大流为8。

3.4 实验

对比传统算法与KPFC 算法求解图3 的最大流的区别：

算法代码采用C++语言开发，在Visual studio 2019 环境下进行编译运行，下列运行结果均为Visual studio 2019 真实运行结果截图。

图2：KPFC 算法例图

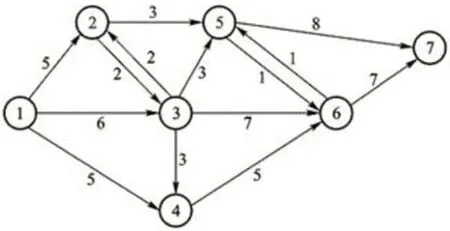
图3：KPFC 算法例图

图4

Isap 算法求解片步骤如下：

首先初始化距离标号和进行GAP 优化的num 数组。

此图一共7 个顶点，从顶点1 到7 的距离标号分别为：3,2,2,2,1,1,0，可以看出，距离标号1 的数量是2，2 的数量是3，3的数量是1，然后结合距离标号寻找第一条增广路径。

第一条增广路径为1-4-6-7，更新距离标号及num 数组。

从源点到汇点的距离标号分别更新为：3,2,2,4,1,1,0，可以看出，距离标号1 的数量是2，2 的数量是2，3 的数量是1，4 的数量是1.更新距离标号以及num 的步骤（除了初始化距离标号）重复了5 次，找到的增广路径分别为：1-3-6-7，1-3-5-7，1-2-5-7，1-3-6-5-7，最终找出正确的最大流，如图4 所示。

KPFC 算法求解步骤如下：

首先寻找关键顶点。

找到三个关键顶点分别为2，3 和5，kp={2,3,5}开始寻找增广路径。

第一条增广路径为1-4-6-7，发现顶点4 变为无用顶点并且图失去连通性，加入拥有最多邻接点的关键顶点3，此时kp={2,5}继续寻找增广路径。

找到的第二条增广路径为1-3-6-7，发现图失去连通性，加入关键顶点5，在此基础上继续找到新的关键顶点6，此时kp={2,6}继续寻找增广路径。

寻找到第三条增广路径为1-3-5-7，图失去连通性，加入关键顶点6，此时kp={2}，继续寻找增广路径。

找到的第四条增广路径为1-3-6-5-7，发现顶点6 变为无用顶点并且图失去连通性，加入关键顶点2，在此基础上找到新的关键顶点3，此时kp={3}，继续寻找增广路径。

加入顶点2 之后，寻找到第五条增广路径为1-2-5-7，图失去连通性，加入关键顶点3，继续寻找增广路径，发现图失去连通性，并且不存在关键顶点，算法结束。

得到正确的最大流为14，与ISAP 算法相比，KPFC 算法去掉了距离标号的初始化，减少了每找到一条增广路径后，对距离标号的计算步骤，KPFC 算法增加了每次找到增广路径后对关键顶点的寻找，而并不是每一次寻路之后都有新的关键顶点，所以总的来说，KPFC 算法优于Isap 算法[6]。

4 结束语

未来对于最大流问题的研究还需考虑遍历算法的改进，让算法具有更聪明的预判能力，尽量减少寻找增广路径的随机性。本文主要对反向边机制做出了改进，没有对增广路径的寻找进行深度优化，在以后的研究中，多条增广路径，可结合最大可行流的概念，做出最优的选择，进一步提高算法效率，总体原则为，用最少的计算步骤，达到问题的最大简化效果。在公共资源越发紧缺的情况下，算法与实际情况的结合，算法在实际问题中的部署与应用，是我们今后应该努力的方向，毕竟能够解决实际问题，才是研究算法真正的意义所在。