基于微分方程的广告费模型探究

燕芊宇

摘要：在商业活动中，产品的生产与销售是两个最主要的环节，直接影响到企业的利益盈亏，是企业能否发展壮大的关键命脉。越来越多的企业意识到产品宣传的重要性，而如何在产品的宣传与销售中科学投入广告费用，实现利益最大化，是本文研究的主要内容。用数学建模方法去解决实际商业活动中的问题，是提升我们将理论运用于实际的有效途径。本文在一定条件下，综合考虑产品生产和宣传成本，售价与销量的一定关系和广告对商业利益的影响，运用曲线拟合和微分方程模型建立选择最优方案，使产品所得利润最大化，让资源充分利用。

Abstract： In business activities， the production and sales of products are the two most important links， which directly affect the profit and loss of enterprises and are the key lifeblood of the enterprise development. More and more companies are aware of the importance of product promotion， and how to scientifically invest advertising costs in product promotion and sales to maximize benefits is the main content of this article. Using mathematical modeling methods to solve problems in actual business activities is an effective way to enhance our application of theory to practice. Under certain conditions， this article comprehensively considers the cost of product production and promotion， the certain relationship between sales price and sales volume， and the impact of advertising on business interests. It uses curve fitting and differential equation models to establish and select the optimal solution in order to maximize the product's profit and make the most of resources.

關键词：微分方程模型;曲线拟合;利润最大化

Key words： differential equation model;curve fitting;profit maximization

中图分类号：O175                                          文献标识码：A                                  文章编号：1006-4311（2020）03-0274-03

1  微分方程模型的基本原理

微分方程模型是研究事物变化的有力工具，在科技、工程、管理、环境和人口问题等解决中发挥着巨大的作用。在许多实际问题中，直接导出变量之间的函数关系较为困难，但导出包含未知数的导数或微分的关系式较为容易时，可用建立微分方程模型的方法来研究该问题[4]。微分方程模型本质是一个动态模型，揭示了实际对象的某一特性随时间或空间的变化而演变的过程。通常我们可以用微元分析法、模拟近似法和根据规律列方程的方法来建立微分方程模型[2]。

2  实际问题

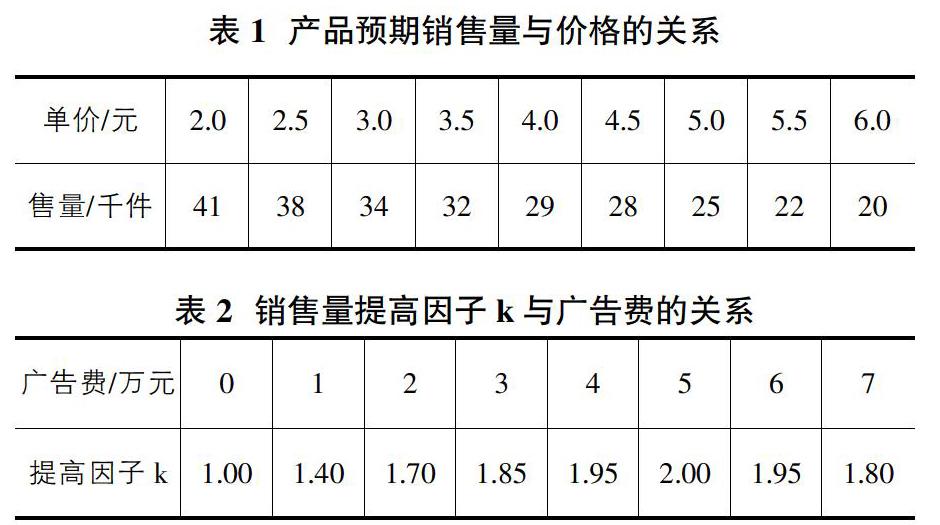
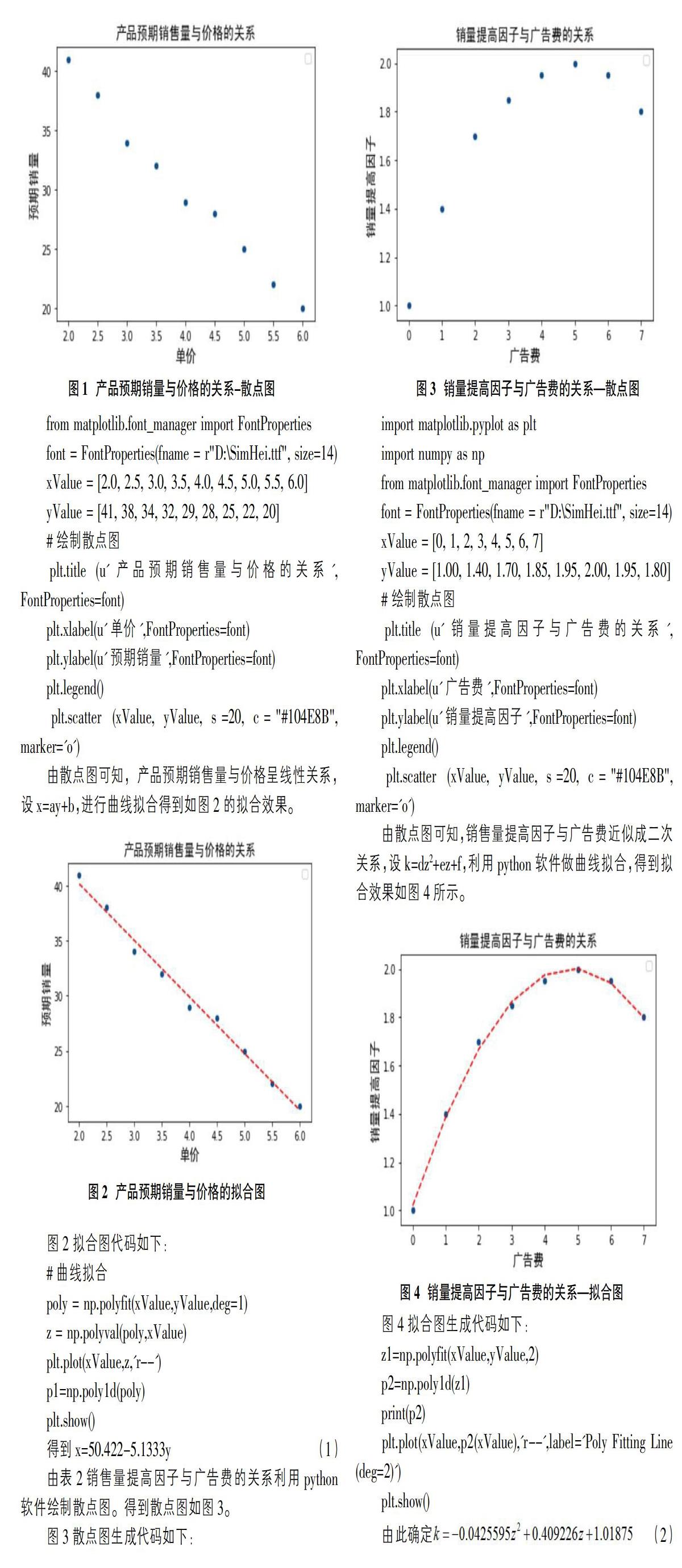
某公司生产的一批产品需要出售，根据统计资料，零售价提高则销售量减少，数据见表1，如果做广告可以使销售量增加，具体增加量用销售量提高因子k表示，k与广告费关系见表2。

已知产品的进价是每件2元，问如何确定产品的价格和花多少广告费，可以使公司获利最大？

3  问题分析

要确定产品的价格与花多少广告费可以使公司获利最大，是本文研究的主要内容，由于已知产品实际销售量与价格的关系表和销售量提高因子和广告费的关系表，所以我们可以从这两种数据出发，分别对每组数据进行曲线拟合，找到线性或者非线性关系，为微分方程模型的建立做准备。微分方程模型建立以后，根据极大值原理，求解即可。

4  模型建立

4.1 符号约定

4.2 曲线拟合

5  总结

商业活动是推动我国经济发展的主要动力，在广告费投入研究中，运用科学的曲线拟合与微分方程建模方法，对问题进行科学分析，得到理想的建模结果，有利于企业最大化盈利，对企业的科学决策具有重大的积极影响。这种模型也将一定会被用于商业活动的其他重要环节，比如如何根据市场需求制定合理的生产计划等，这也是未来的主要拓展方向。总之，基于微分方程模型科学指导商业经营活动是未来有意义的研究课题，值得我们持续研究。

参考文献：

[1]张亮忠.数字测图技术[M].南京：建筑出版社，1991.

[2]王高雄，等.常微分方程[M].北京：高等教育出版社，2001，1.

[3]李大潜.将数学建模思想融入数学类主干课程[J].大学数学，2006，1.

[4]赵静，但琦.数学建模与数学实验[M].二版.武汉大学出版社，2005.

[5]云舟工作室.数学建模基础教程[M].人民邮电出版社，2001，7.

[6]杨桂元，李天胜，徐军.数学模型应用实例[M].合肥工业大学出版社，2007.

[7]沈娟.高职微分方程教学中融入数学建模思想[J].价值工程，2013，32（24）：222-223.