隐含语义模型在推荐系统中的应用研究
2020-02-02陈功平
王 红,陈功平
(六安职业技术学院 信息与电子工程学院,安徽 六安 237158)
0 引言
推荐系统[1]将用户(User)可能感兴趣但无关的项目(Item)生成列表提供给用户.推荐系统已普遍应用于电子商务、新闻、视频等各种应用系统中,在计算机和各种移动终端设备的应用中起到良好的推荐效果.推荐结果的准确度是评价推荐算法[2]优劣的主要依据,此外还要考虑时间和空间复杂度.
推荐算法在研究用户和项目的历史行为后,才可以更好地为用户完成推荐,将项目更准确地推荐给客户.推荐系统多采用预测模式,认为用户的兴趣不会在短时间内剧烈变动、改变原有喜好.比如,通过历史行为得出某人喜欢武侠小说,那么系统会将和该用户喜好高度一致的用户已阅读的武侠类图书推荐给该用户.
1 LFM模型
1.1 简介
隐含语义模型[3](Latent Factor Model,LFM)是通过隐含特征(Latent factor)将用户和项目联系起来.基于用户和基于项目的推荐算法都是通过训练集聚类用户和项目,有明确的目的,而隐含语义模型使用用户历史行为统计自动聚类,可以很好地自动分类物品所属的种类,而不需要人为的分类.
公式(1)是LFM模型中计算用户u对项目i感兴趣程度的计算公式.

其中pu, k 和qi, k 是模型的参数,pu, k 代表用户u和第k个隐类之间的兴趣关系,qi, k 代表项目i和第k个隐类之间的兴趣关系,这两个参数,连接了用户u和项目i,可以计算出用户u对项目i的感兴趣程度.
1.2 计算过程
1.2.1 LFM建模
图1中的矩阵R表示用户u和物品i的行为数据集(这里以3个用户和4个物品为例),矩阵值Rij表示用户i对项目j的兴趣度,使用LFM对其建模,得到矩阵P和Q.
LFM算法的计算思路[4]为:从用户项目行为数据集中设置若干主题即隐类的数量,作为用户和项目之间的联系,即把原有的用户项目矩阵R分解为P矩阵和Q矩阵积.其中P矩阵表示“用户-类”,矩阵值Pij表示的是用户i对类j的兴趣度,值越高表示用户i对j类的兴趣度越高;Q矩阵表示“类-项目”,矩阵值qij表示的是项目j在类i中的权重,权重越高越能作为该类的代表.

图1 LFM建模
1.2.2 LFM模型的优点
从图1的LFM模型建模可以看出,该模型有以下几个优点.
(1)分类粒度可设置[5],图1将项目item分了c1、c2和c3三个类,类的数量可以通过设置LFM模型的分类数就可控制分类粒度,分类数越大,粒度越细,类别就越多.
(2)无需手动设置类别[6],矩阵P、Q中类别C的数量可设置,类中最具代表性的项目item是基于用户行为数据集R自动聚类产生的,因此不需要用户手动分类项目,既可以免去手动分类劳动还可以减少手动分类的错误.
(3)项目item并不是明确地被划分到某个类,而是计算item属于某类的概率,即qij值越高代表项目j在属于类i的概率越高.
(4)可以得到每个用户user对所有类的兴趣度,即使该用户没有实际产生某类的行为数据,也可以通过模型计算出用户对该类的隐含兴趣度[7].
1.2.3 参数值的计算
使用最优化损失函数[8]求解矩阵P和Q中的puk和qik参数值.将所有用户user和他们有过行为(即表示喜欢)的item构成item全集.对于每个user,把有过关联的item称为正样本,将兴趣度Rui定义为非负数,这里规定为Rui=1,此外还要定义负样本,负样本的数量要和正样本数量相当,且应从item全集中随机选择,将其兴趣度Rui定义为0,即Rui=0.即user对item的兴趣取值范围为[0,1].
采样后得到一个新的user-item集K={(U,I)},如果(U,I)是正样本,则RUI=1,否则RUI=0.损失函数如公式(2)所示.
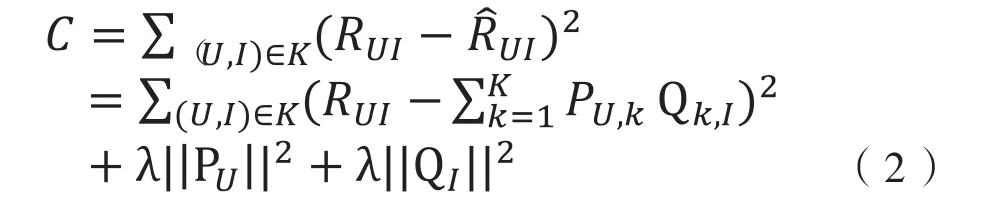

其中,α是学习速率[10],α越大,迭代下降的越快.α和λ一样,也要根据实际应用场景反复实验得到.
2 基本LFM模型推荐实验
2.1 数据集介绍
使用100k的MovieLens[11]数据集验证基本LFM模型推荐算法,数据集中存储了10万条用户对电影的评分,每行由用户编号(uid)、电影编号(mid)和评分值(score)组合而成,评分值为1到5的整数,数据集情况如表1所示.

表1 数据集简介
根据LFM算法,生成的P矩阵有943行f(f为类别的数量),实验中要验证f类别取值对评分正确的影响;Q矩阵应有f行1682列.
实验数据按照8:2的比例随机分成训练集train和测试集test,训练集用于训练推荐算法的各项参数,测试集用于测试推荐算法的有效性.
2.2 LFM模型的学习
2.2.1 初始化矩阵P和Q
使用随机数和F(种类)的平方根成正比的方式初始化,初始化方法与训练集无关,即将每个p[u, f]和q[f, i]都填充为0到1的随机数.算法伪码如下.

2.2.2 LFM模型的学习迭代
迭代是为了训练输出矩阵p和q,算法输入训练集train,F类别个数,n是迭代次数,alpha为学习参数,lambda是正则化参数,注意每次迭代后,学习参数alpha应有衰减.算法伪码如下.


在上述迭代过程中用到的Predict(x,y,p,q)方法是使用p和q矩阵预测用户x对y的评分,并依此来一次次修正p和q矩阵的取值.
2.2.3 LFM模型的测试
使用test数据集预测用户u对物品i的评分,预测算法的伪码如下.

2.2.4 实验结果与分析
使用均方根误差RMSE[12-13]作为算法的评价指标,RMSE反映的是预测分值与用户实际分值间的差异,值越小说明预测越准确.RMSE的计算公式如(7)所示.

表2是LFM基本模型的推荐结果,其中F表示类别数,n是迭代次数,alpha和lambda是参数,RMSE是评价指标.
从结果可见,当alpha和lambda的值都取0.02时,结果较好.迭代次数为20和100时效果较好.隐类F的取值对实验结果影响较小,当值在50-200之间效果较好,因此在第3节改进算法中F值取100.
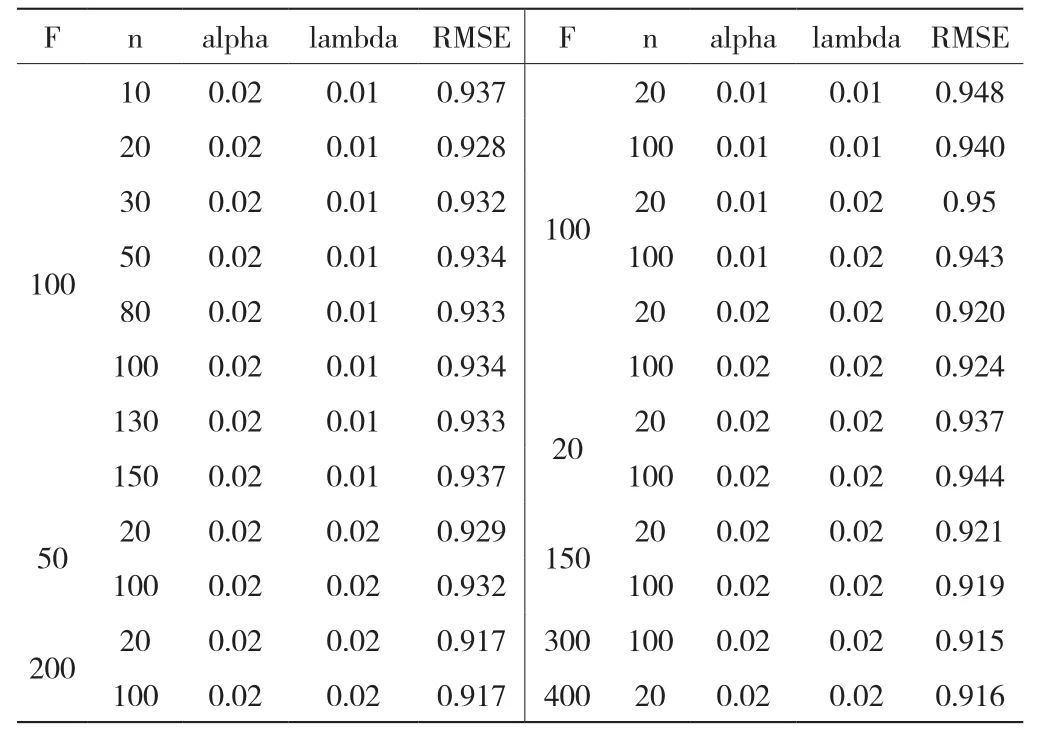
表2 基本LFM模型实验结果
图2是当F=100,alpha=0.02,lambda=0.01时,RMSE值随n值的变化.可以看出,当n=20和n=130时,RMSE值最低,即实验效果最好.由于迭代次数越多训练时间越长,因此在改进算法中只验证n=20和n=100时的实验效果.
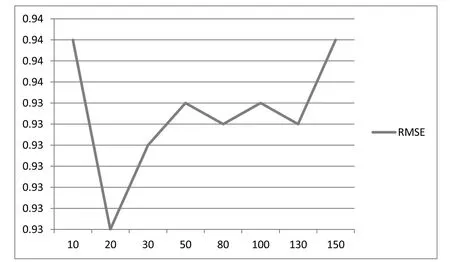
图2 RMSE随n值变化的效果
3 改进的LFM模型实验
3.1 改进策略
LFM模型的分数预测通过隐类将用户和物品联系起来[14],但实际情况下,评分系统有些固有属性和用户、商品是无关的,比如某些用户偏好评价高分,有些商品的质量确实好,所有用户都会给高分,基于此原理,对基本LFM模型加以改进,增加3个偏置项,加入后,评分预测公式如公式(8)所示.

其中,μ是train数据集中评价的平均分,表示该评价系统中其他用户的评分规律对预测的影响;表示train数据集中用户的评分偏好,比如某些用户无论电影优劣都喜欢给差评;表示项目的本身的优劣,比如某些电影确实很好,分数很高[15].
3.2 实验结果与分析
根据基本LFM实验结果,其他参数的设置如表3所示.
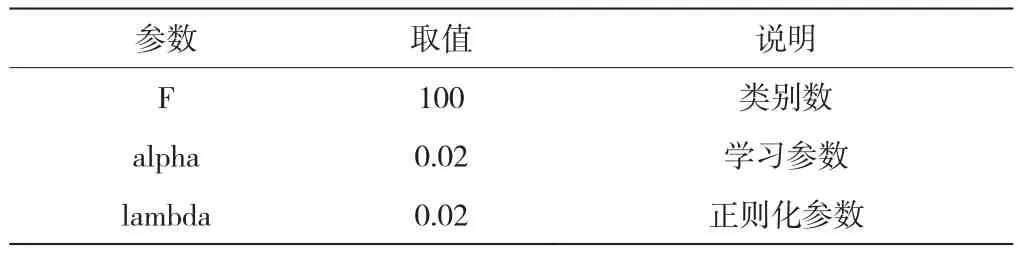
表3 改进LFM模型的参数设置
当n分别取20和100时,改进后的LFM模型和基本LFM模型推荐效果如表4所示.

表4 改进后的LFM和基本LFM模型实验结果比较
图3是两种推荐模型推荐效果的折线图,从表4和图3可以看出,改进后的推荐模型推荐效果明显优于基本模型,可以证明推荐改进效果成立.

图3 推荐效果折线图
4 结束语
增加软件评分偏好、个人评分偏好和项目评分偏好的LFM模型可以有效地提升推荐效果,对减少评分矩阵的稀疏度、填充用户评分矩阵有很好的推广价值,改进后的LFM模型推荐算法比基本LFM模型的性能更优.此外,该模型还可以很好地解决新项目和新用户(即冷启动)推荐问题.
