基于神经网络PID的丘陵山地拖拉机姿态同步控制系统

2020-02-02张锦辉李彦明齐文超刘成良杨福增李政平

农业机械学报 2020年12期

张锦辉李彦明齐文超刘成良杨福增李政平

(1.上海交通大学机械与动力工程学院，上海 200240； 2.西北农林科技大学机械与电子工程学院，陕西杨凌 712100；3.山东五征集团，日照 276800)

0 引言

我国丘陵山地地形分布广泛，其面积占陆地总面积的43%以上。由于缺乏丘陵山地的农业机械，因此给农业生产带来了诸多不便[1]。丘陵山地坡度一般为6°～15°，拖拉机作业时容易导致耕深不均匀和发生侧翻，影响了作业效率和农作物的生长[2]。拖拉机在路面崎岖的丘陵山区作业时，根据丘陵山地的作业环境特点，设计车身横向姿态调整系统能够有效提高驾驶舒适性和安全性，设计机具横向调整系统能够使机具与路面保持水平状态，有助于保证耕深均匀，提高作业效率和作业质量[3]。

目前，国内外对丘陵山地机械调整系统的研究主要集中在车身调平方面，对后桥机具[4-8]作业姿态的同步控制研究尚处于起步阶段。在车身调平方面，COLOMBO等[9]研究的自动调平系统通过一套液压气动悬架来保证拖拉机驾驶室的水平状态。PIJUAN等[10]研究的悬挂机构可以主动调节自身高度，进而进行底盘调平，但控制精度较低。文献[11-15]研究了一种适用于微型履带山地拖拉机的液压差高机构，采用PID算法实时计算机构的期望位置，实现车身调平。胡春辉等[16]设计了一种应用于农田清平机的三点调平系统，并进行了试验验证，其精度和速度均较为理想。在机具姿态调整方面，邵明玺等[2]提出了基于模糊PID控制的双液压缸横向位姿调整系统，通过液压缸活塞位移带动机具产生横向角度，以实现机具与地面的平行,但该系统简单使用车身倾角替代地面倾角，难以满足实际使用需求。刘林[17]设计的机具调平系统实现了机具的全自动调平，提高了系统的可靠性，但由于使用电磁换向阀来控制液压缸运动，其控制精度有待提高。

目前，国内外研究主要单独针对车身或者机具姿态控制展开，缺乏对车身和机具同步姿态控制的研究。同时，现有丘陵山地拖拉机姿态主动调整系统姿态调整方案功能单一、适应性和实用性有限，难以满足复杂多变的作业需求。针对车身和机具姿态实时调整需求，本文采用神经网络PID算法设计丘陵山地拖拉机车身-机具姿态同步控制系统，进行仿真和试验，并与常规的PID算法进行对比。

1 控制系统设计及运动学分析

丘陵山地拖拉机姿态控制系统示意图如图1所示。由于拖拉机整车重心、驾驶室位置均位于后驱动桥，且前驱动桥为随动系统，前、后桥由一单自由度旋转轴连接。因此，本文设计的车身横向调平装置安装在后驱动桥，不会对前轮造成影响。

车身横向姿态调整系统通过偏心摆动机构的转动，带动安装在偏心摆动机构末端的车轮中心，产生相对位移h，进而使后驱动桥产生横向角，调整车身保持横向水平。

机具横向姿态调整系统以计算得到的实时路面倾角作为目标倾角，通过旋转液压缸的伸缩运动，带动旋转架、机具绕旋转轴转动，产生横向角度，使机具横向倾角与路面保持平行。

1.1 车身横向姿态调整系统设计

车身横向姿态调整系统安装实物图如图2a所示，其核心组成部件包括车身横向倾角传感器和液压马达驱动的左、右偏心摆动机构，及对应的摆角传感器。车身横向倾角传感器安装于后驱动桥箱上方车身，左、右摆动机构分别安装于半轴套管与车轮之间，左、右摆角传感器安装于对应的摆动机构。

摆动机构示意图如图2b所示，摆动机构由2个比例阀控液压马达控制其摆动速度和摆动方向。左、右摆角传感器安装平面与水平面之间的夹角分别为左、右摆角α1和β1，半轴中心与驱动轴中心连线的长度为摆动半径l。为保证车辆正常行驶，两侧摆角应大小相同，方向相反，摆角范围为(-80°，80°)。由图2b可知，当α1和β1均为0°时，驱动轴轴心与后驱动桥轴心在同一平面上，此时，在垂直方向上的相对位移h=0。当摆动机构转动一定角度时，驱动轴与半轴中心会产生一定的高度差h，以左轮为例，此时有

h=lsinα1

(1)

图2c给出了车辆未进行姿态调整时，简化后的车身姿态调整系统示意图。图中，点A、B分别表示左、右半轴中心，两点之间的距离为后桥长度L，车身横向倾角传感器安装平面与水平面的夹角为θ1。

车身调整后，后驱动桥应与水平面平行，即点A、B连线与水平面平行。未调整时，点A、B与水平面之间的高度差H为

H=Lsinθ1

(2)

为保持后桥水平，需驱动摆动机构转动一定角度，使点A、B分别上升、下降H/2，即h=H/2，如图2d所示。控制器通过CAN总线实时接收车身横向倾角传感器和左、右摆角传感器的数据，计算比例阀的输出电流，从而控制摆动机构转过一定的摆角，实现车身横向调平控制。

1.2 机具横向姿态调整系统设计

机具倾角需要在作业过程中随地形起伏进行调节，使之与当前的地面倾角基本一致。拖拉机、机具姿态调整机构、机具的安装实物图如图3a所示。其主要组成部件包括机具横向倾角传感器、旋转液压缸和旋转架。机具姿态调整机构示意图如图3b所示，调整机构通过上拉杆和牵引架上安装的两个下拉杆与拖拉机用球销进行连接，机具通过上连接杆和两个下连接板与调整机构用球销进行连接，下连接板通过定位螺栓安装于旋转架。如图3c所示，在旋转架一侧安装机具横向倾角传感器，用于实时检测机具的实际倾角，机具横向倾角传感器实时测量机具的实际倾角，其安装平面与水平面的夹角即为机具横向倾角γ1，上转轴与旋转轴中心连线长度为S1，转轴连杆长度为S2，旋转液压缸及其连杆总长度为S3。由几何关系可得

(3)

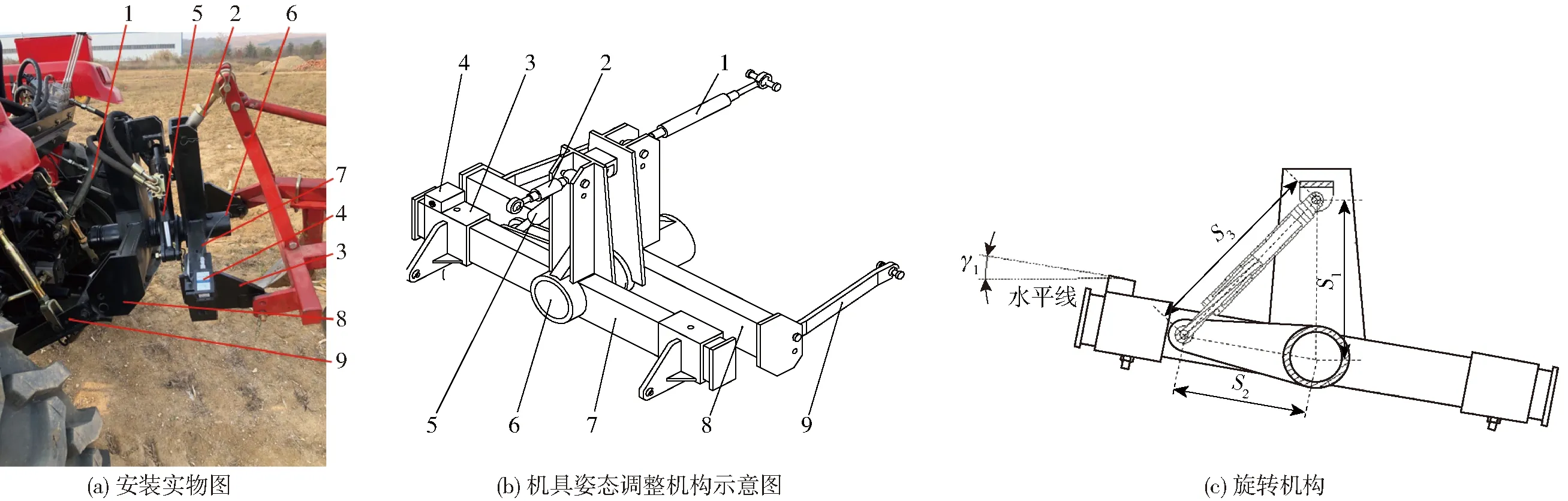
图3 机具姿态调整机构实物图与示意图Fig.3 Schematics of attitude adjustment mechanism of implement1.上拉杆 2.上连接杆 3.下连接板 4.机具横向倾角传感器 5.旋转液压缸 6.旋转轴 7.旋转架 8.牵引架 9.下拉杆 10.转轴连杆

旋转液压缸的直线伸缩通过转轴连杆和旋转轴带动旋转架旋转，进而控制悬挂的机具转动，实现机具姿态控制，机具横向倾角调整范围为(-20°， 20°)。

为保证机具与地面的横向平行关系，机具的目标倾角应等于当前的路面倾角。控制器接收机具横向倾角传感器测得的角度，结合车身横向倾角传感器和左、右摆角传感器的数据，计算比例阀的输入电流，从而控制机具转动，实现机具姿态控制。

1.3 同步控制原理

控制系统框图如图4所示，图中θ为车身目标倾角，在本系统中θ=0°，θ2为根据左、右摆动机构摆角计算出的车身与路面夹角，α0为左摆动机构目标摆角；β0为右摆动机构目标摆角；机具的目标倾角与路面实际倾角相等，Iα、Iβ、Iγ分别为左比例阀、右比例阀、机具比例阀的输入电流。

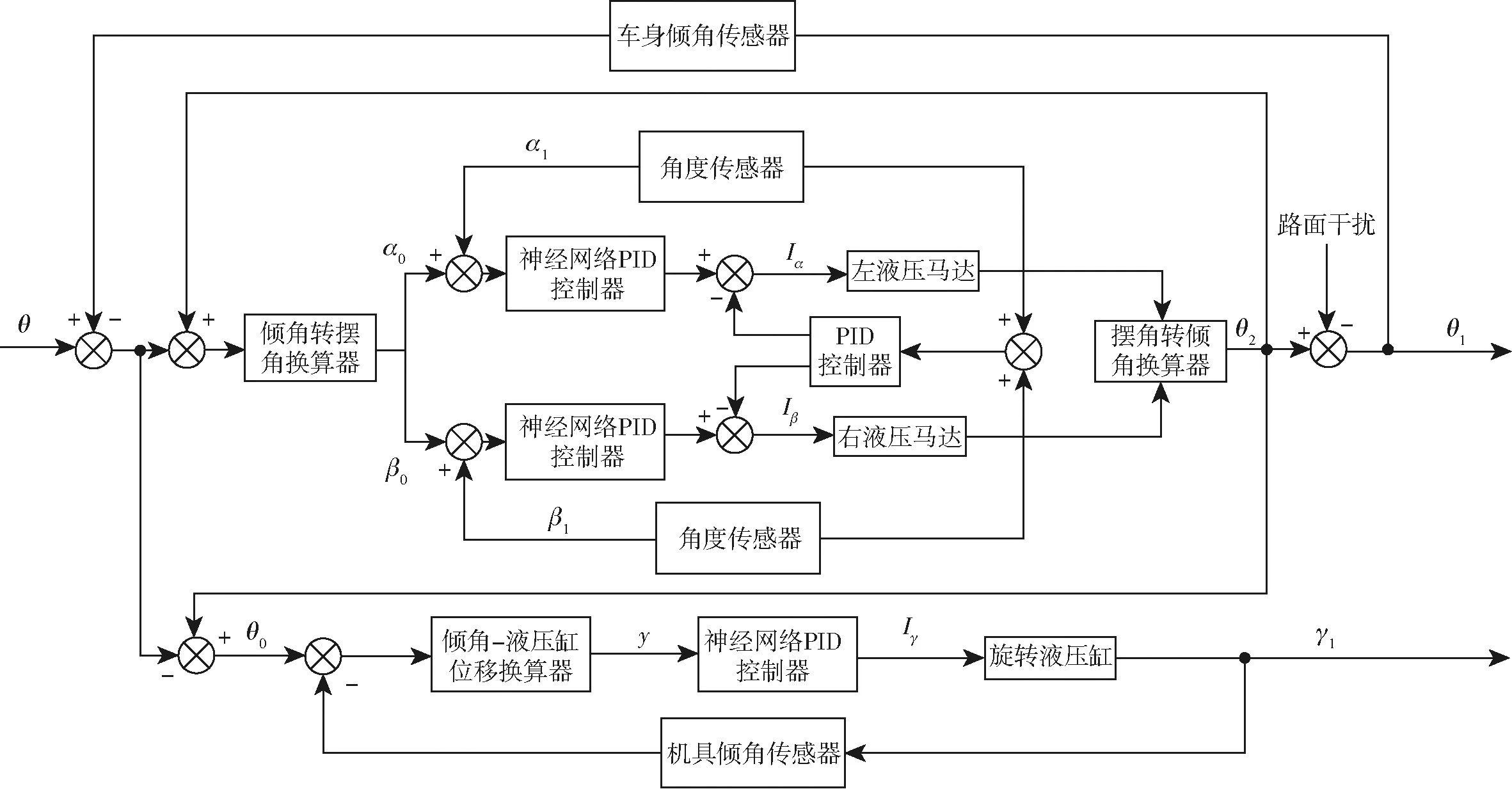
图4 姿态同步调整控制框图Fig.4 Attitude coordination adjustment control block diagram

基于神经网络PID算法的同步控制原理为：主控器接收车身横向倾角传感器和左、右摆角传感器的数据，计算两侧摆动机构应该摆动的角度；同时，据此计算出当前路面倾角，作为机具控制系统的目标倾角θ0，且有

θ0=θ1+θ2

(4)

由系统控制框图车身姿态控制系统的外环神经网络PID和机具控制系统的神经网络PID控制器使执行机构运动到目标位置，车身姿态控制系统的内环PID控制器保证了在调整过程中，两侧摆动机构摆角满足大小相等、方向相反的要求。

其中，结合式(1)、(2)可得出倾角转摆角换算器和摆角转倾角换算器计算公式为

Ltan(θ-θ1+θ2)=lsinα0-lsinβ0

(5)

lsinα1-lsinβ1=Ltanθ2

(6)

结合式(3)可得出机具倾角-液压缸位移换算器计算公式为

(7)

式中y——液压缸位移，m

2 系统建模与控制器设计

2.1 系统建模

同步控制系统通过控制比例阀控马达系统和比例阀控液压缸系统，对车身姿态和机具姿态进行调整。为便于控制器设计和仿真，需对液压马达和液压缸系统进行数学建模。

为简化讨论，建模过程中的阀系数取值均取零位系数，将固有频率较高的电液比例伺服阀近似看做比例环节。车身、机具等机械结构转动产生的负载力矩(或负载力)均计算在总负载力矩(或总负载力)上。

2.1.1阀控液压马达系统模型

对于系统中惯量较大的阀控液压马达，不考虑弹性负载的作用，其数学模型可表示为

(8)

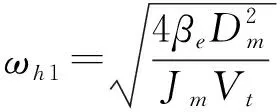
(9)

(10)

式中ωh1——液压马达液压固有频率，rad/s

ξh1——液压马达液压阻尼比

I——通入比例电磁铁电流，A

TL——液压马达和车身折算在马达轴上的总负载力矩，N·m

θm——液压马达转角，rad

Kq1——阀控马达系统中比例阀的流量增益系数

Bm——液压马达粘性阻尼系数

Ksv——比例阀比例系数

βe——油液有效体积弹性模量，Pa

Dm——液压马达理论排量，m3/rad

Jm——折算到马达轴上的总惯量，kg·m2

Vt——阀腔、马达腔与连接管道总容积，m3

Kce——阀控液压马达系统总流量压力系数，m5/(N·s)

考虑到后车身质量大，转动惯量大，因此需考虑液压马达轴上的总负载力矩TL在车身横向调平过程中，由于车身转动产生的力矩。后车身受力简图如图5所示。

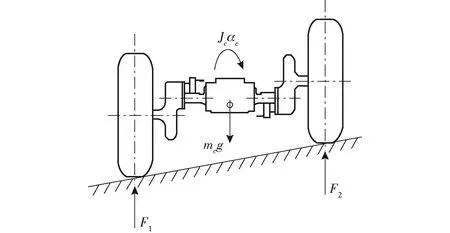
图5 后车身受力简图Fig.5 Schematic of rear body force

由力平衡方程和力矩平衡方程结合式(1)可得左、右液压马达负载力矩分别为

(11)

(12)

式中TL1——左液压马达负载力矩，N·m

TL2——右液压马达负载力矩，N·m

mc——后车身质量，kg

Jc——后车身转动惯量，kg·m2

αc——车身横向倾斜角加速度，rad/s2

2.1.2阀控液压缸系统模型

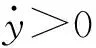
(13)

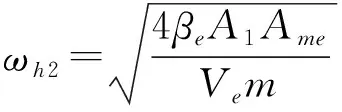
(14)

(15)

式中ωh2——液压缸液压固有频率，rad/s

ξh2——液压缸液压阻尼比

m——活塞及负载总质量，kg

f——机具及旋转架折算在活塞上的总负载，N

Kq2——阀控液压缸系统中比例阀的流量增益系数

A1——无杆腔活塞有效面积，m2

Bp——活塞及负载粘性阻尼系数

Kt——阀控液压缸系统总流量压力系数

同理，考虑到旋转架等机械结构的转动惯量，由力矩平衡方程，结合式(3)可得，作用在液压缸活塞上的总负载f为

(16)

式中Jt——机具及旋转架转动惯量，kg·m2

αt——机具横向倾斜角加速度，rad/s2

2.2 BP神经网络PID控制器设计

控制器通过调节比例系数Kp、积分系数Ki、微分系数Kd，改变3个单元的增益，提高系统的动态性能和稳态性能。

常规的PID控制器参数整定方法包括基于参数最优化的整定方法、基于对象参数辨识的整定方法等[20]，利用2.1节建立的被控对象数学模型，通过控制器参数与系统动态和稳态性能之间的定性关系，采用试验法进行参数整定[21]。具体步骤为：

(1)为减少需整定的参数，采用PI控制器，即Kd=0，为保证系统稳定，比例系数Kp的初始值不能太大。

(2)给出阶跃输入信号，如阶跃响应超调量过大或系统发生振荡，无法收敛于期望输出，则减小Kp，增大Ki，如没有超调，但响应缓慢，则按相反方向调整。在调节过程中，如消除误差的速度较慢，也可适当减小Ki。

(3)如果反复调整Kp、Ki，仍存在较大超调，则加入微分控制，Kd从0开始逐渐增大。反复试验后，取综合性能最好的参数组合[22]。

上述PID控制器参数需经多次试验调整，且一旦确定，在系统运行过程中无法改变。分析2.1节建立的电液系统数学模型可知，由于电液系统存在死区、压力-流量增益等非线性特性，对其进行数学建模时，需要进行合理的假设，将非线性特性进行局部线性化，但这种线性化处理会影响到系统的动态特性[23]。而BP神经网络可以实现任意非线性映射[24-26]，利用神经网络可以建立参数自整定的PID控制器，从而优化控制系统的静态和动态性能。基于BP神经网络的PID控制系统结构框图如图6所示。控制器由经典增量式PID控制器和BP神经网络组成。

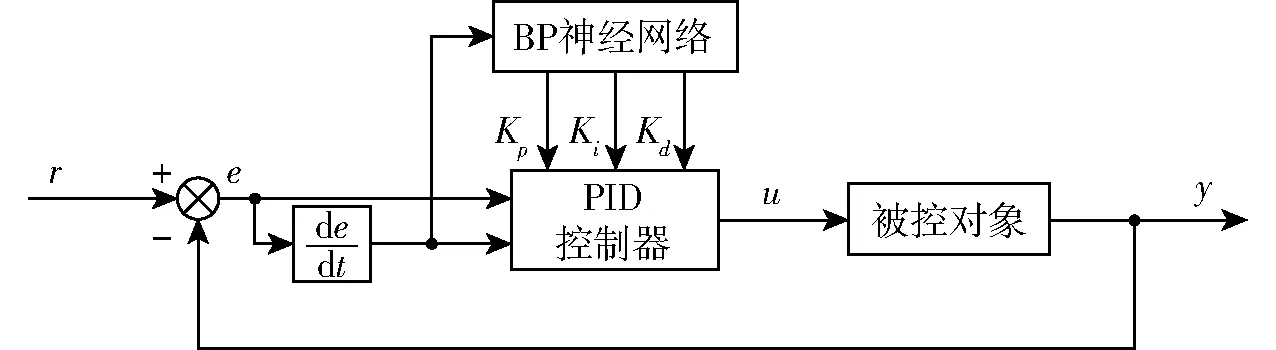
图6 基于BP神经网络的PID控制系统结构框图Fig.6 Block diagram of PID control system based on BP neural network

采用经典增量式数字PID控制，其计算公式为[27]

u(k)=u(k-1)+Kp(e(k)-e(k-1))+Kie(k)+
Kd(e(k)-2e(k-1)+e(k-2))

(17)

式中u(k)——k时刻控制器输出的电流

e(k)——k时刻的控制偏差

对于2.1节所述液压马达系统，e(k)为k时刻目标摆角与实际摆角的差值；对于液压缸系统，e(k)为k时刻路面实际倾角与机具横向倾角的差值。

本文控制算法使用的神经网络采用4-5-3结构的BP网络。其中隐含层神经元的激励函数采用正负对称的双曲正切函数，PID控制器的3个参数均为非负值，因此，输出层的激励函数采用非负的Sigmoid函数。

根据控制框图，神经网络输入层输出选定为

(18)

神经网络隐含层输入为

(19)

输出为

(20)

神经网络输出层输入为

(21)

输出为

(22)

其中

f(x)=tanh(x)

(23)

(24)

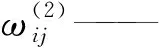
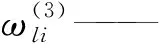
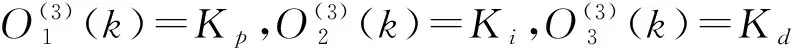
式(18)～(22)中，上标(1)、(2)、(3)分别对应输入层、隐含层和输出层。

在神经网络前向传输过程中，取性能指标J来判断当前PID参数，性能指标J计算公式为

(25)

正向传播计算完毕后，根据实际输出与期望输出的误差按连接通路进行反向计算，对各层之间的权值进行调整，以优化性能指标J，即减小误差信号。利用最速下降法推导得到输出层权值调整公式为

(26)

其中

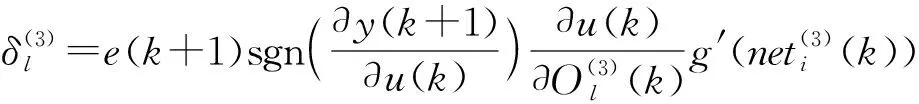
(27)

式中η——学习速率，取0.3

α——惯性系数，取0.05

隐含层权值调整公式为

(28)

其中

(29)

根据以上推导可知，在控制过程中，若实际输出与期望输出不一致，各层神经元之间的权值进行自动实时调整，进而调整输出层输出，实现PID参数的自整定。

3 仿真分析

使用Matlab中的可视化仿真工具Simulink建立丘陵山地拖拉机姿态系统控制系统动力学模型，利用S-function模块搭建神经网络PID控制器，结合2.2节中建立的数学模型，通过试验法对控制器的比例、积分、微分系数进行整定，即可对模型进行仿真。系统主要模型参数如表1所示，Simulink仿真模型如图7所示。

一般来说，丘陵山地拖拉机的作业路面倾角范围为(-15°，15°)，车身姿态控制系统中摆动机构的摆角范围为±80°，根据机构设计尺寸可知，路面倾角为15°时，摆动机构摆角为(-75°，75°)，处于安全范围。因此，车身横向倾角初始值为15°，机具横向倾角初始值为0°，给定幅值为15°路面倾角的阶跃信号。

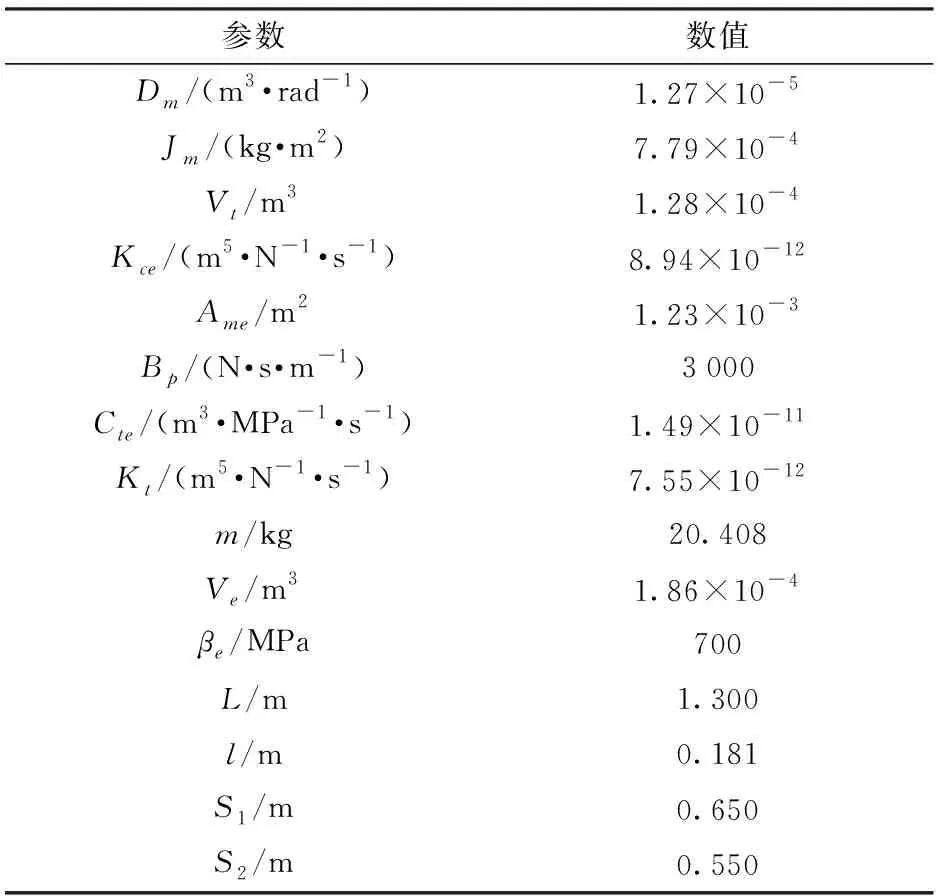
表1 系统模型参数Tab.1 Parameters of system model

仿真结果如图8所示。图8a为PID控制算法的车身调整仿真结果，上升时间为12 s，超调量为0.85°，图8b为神经网络PID控制算法的车身调整仿真结果，调整时间为10.22 s，基本无超调。图8c为PID控制算法的机具调整仿真结果，上升时间为0.71 s，超调量为0.55°，图8d为神经网络PID控制算法的机具调整仿真结果，上升时间为0.66 s，超调量为0.32°。仿真结果验证了神经网络PID控制算法的可行性。同时，神经网络PID控制算法的准确性、快速性均优于PID控制算法。

4 试验

4.1 试验设备与条件

对山东五征集团生产的四轮拖拉机进行改装，安装车身姿态调整机构和机具姿态调整机构。使用自主研发的控制系统控制器，CPU使用意法半导体生产的STM32F407ZGT6型芯片；使用TLE82453型芯片输出PWM电流，控制比例电磁阀，电流为0～1.5 A；使用4个浙江北微信息科技有限公司生产的BW-VG525型动态倾角传感器，分别安装在左右摆动机构、车身、机具姿态调整机构上，实时测量左右摆角、车身横向倾角和机具横向倾角；使用CAN总线通信，用于接收传感器数据。

试验分为2个工况。工况1：在一段坡度相对固定的路面，以约3 km/h的速度进行作业，分别启动PID同步控制程序和神经网络PID同步控制程序，验证方案的可行性，对比、分析同步控制效果；工况2：在一段起伏较大，坡度变化明显的路面，以约3 km/h的速度进行作业，对比PID和神经网络PID在较为恶劣工况下的同步控制效果。试验现场如图9所示。

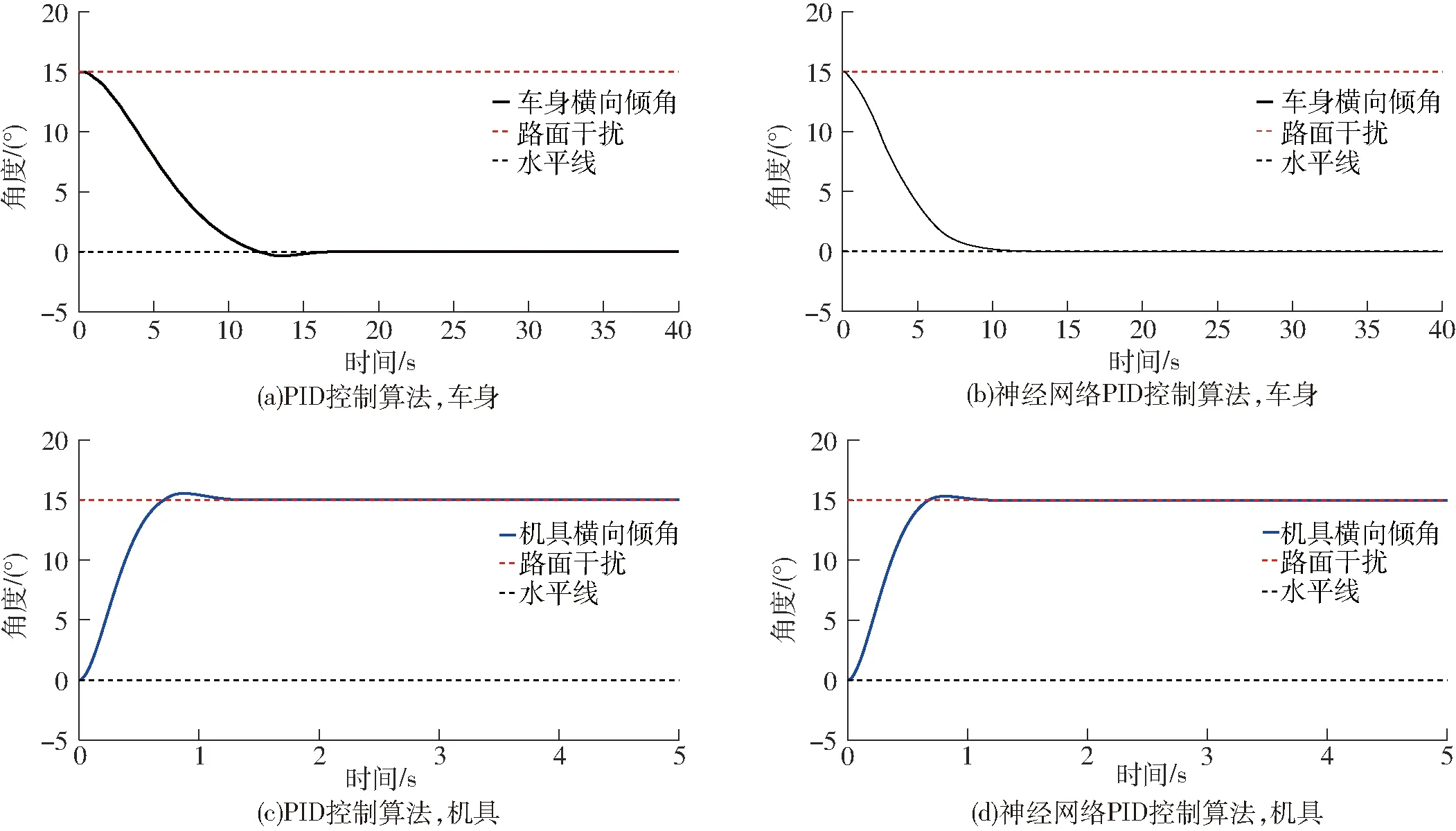
图8 阶跃响应仿真结果Fig.8 Step response simulation results

图9 试验现场Fig.9 Experimental site

4.2 试验结果及分析

4.2.1固定坡度路面试验

固定坡度路面的倾角变化如图10所示，作业路面倾角在14°上下波动，波动范围约±1°，结果表明，可以模拟丘陵山地拖拉机常见的作业工况。

图11a为基于PID算法和神经网络算法的控制方法下的车身姿态调整效果。由图可知，由于路面起伏不大，车身横向倾角变化范围较小。经计算可知，PID算法控制下，车身横向倾角最大误差为0.975 0°，平均绝对值误差为0.178 2°，均方根误差为0.231 1°；神经网络PID算法控制下，车身横向倾角最大误差为0.864 0°，平均绝对误差为0.160 4°，均方根误差为0.225 6°。

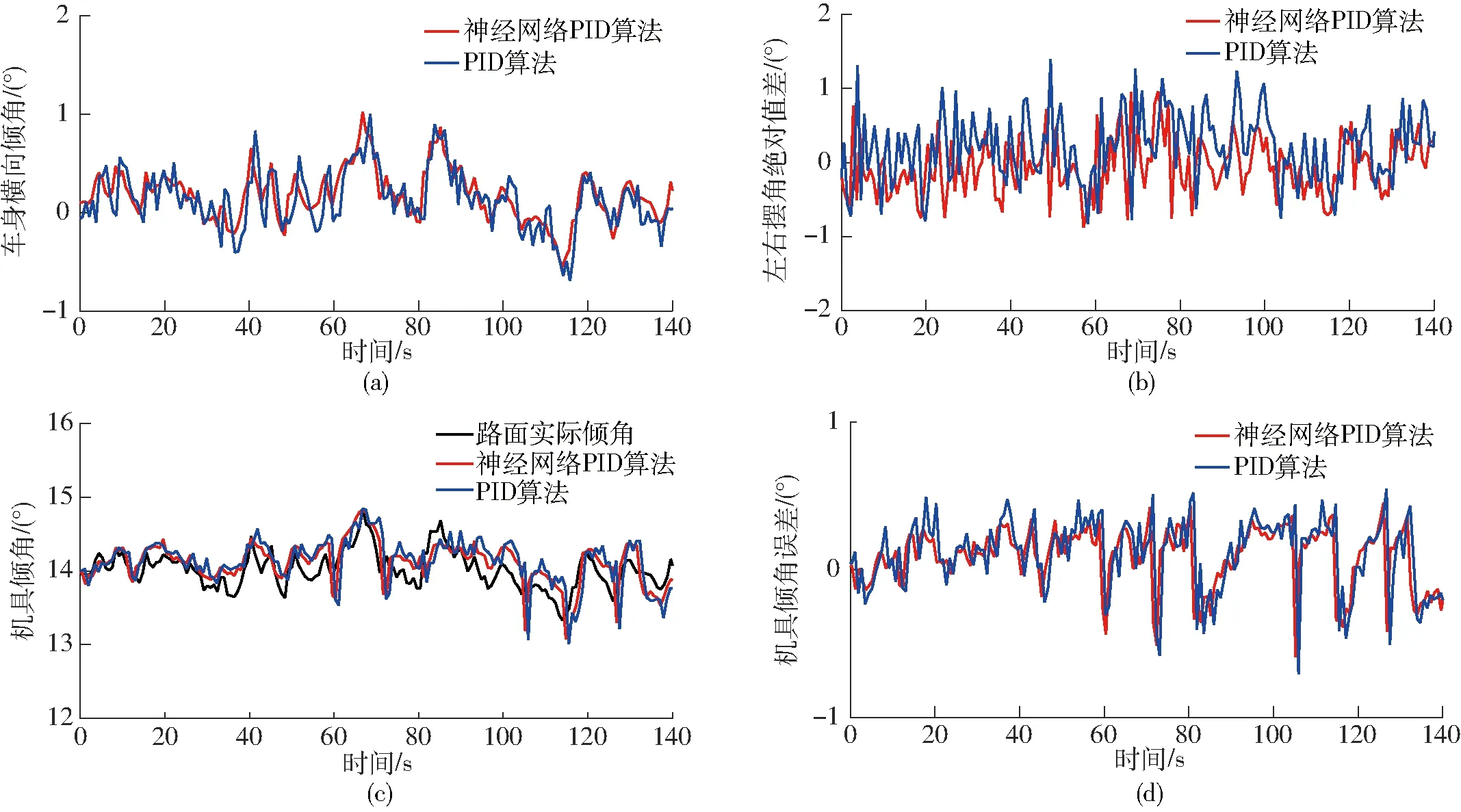
图11 固定坡度路面试验结果Fig.11 Fixed slope road test results

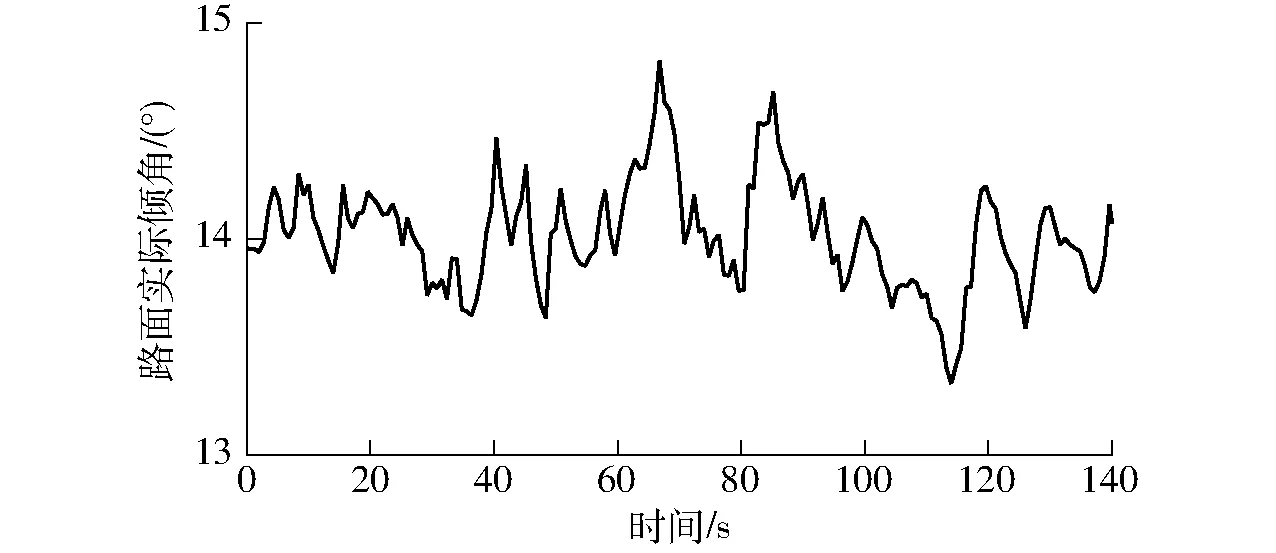
图10 固定坡度路面倾角变化曲线Fig.10 Curve of inclination of fixed slope pavement

图11b为两种算法控制下的摆动机构运动情况。计算可知，PID算法控制下，左右摆角绝对值差最大误差为1.445 0°，平均绝对误差为0.392 1°，均方根误差为0.480 7°；神经网络PID算法控制下，左右摆角绝对值差最大误差为0.960 0°，平均绝对误差为0.351 2°，均方根误差为0.419 0°。在路面坡度变化不大的情况下，所提控制方法能够保证车身横向倾角基本为0°左右，误差范围较小，能够满足丘陵山地拖拉机的常见工况。同时对比可知，神经网络PID控制算法的性能优于常规的PID控制算法。

图11c为两种控制方法下的机具倾角调整情况。由图可以看出，机具倾角随路面实际倾角的变化不断调整，跟踪效果较好。为更直观地比较不同控制方法的性能，分别绘制PID算法和神经网络PID算法控制下的机具倾角调整误差曲线，如图11d所示。计算可知，PID算法控制下，机具横向倾角最大误差为0.779 6°，平均绝对误差为0.200 5°，均方根误差为0.244 2°；神经网络PID算法控制下，机具横向倾角最大误差为0.649 7°，平均绝对误差为0.168 6°，均方根误差为0.201 9°。在角度固定，起伏不大的作业路面，2种控制算法控制误差差别不大，神经网络PID算法相对更优，验证了该方法的可行性。

4.2.2随机坡度路面试验

使用PID算法和神经网络PID算法启动同步控制程序，以1挡作业速度(约3 km/h)行驶在起伏较大的随机路面上，路面倾角变化曲线如图12所示，路面最大倾角约13.5°，倾角极差约为18°，可以较好地模拟出恶劣作业工况。

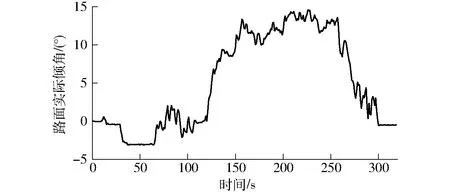
图12 随机坡度路面倾角变化曲线Fig.12 Curve of inclination of random slope pavement

图13 随机坡度路面试验结果Fig.13 Random slope road test results

图13a为基于PID算法和神经网络算法的控制方法下的车身姿态调整情况。对比图10可以看出，在路面倾角变化不大的路面，车身横向倾角基本为0°，在剧烈起伏的路面，车身横向倾角在0°附近小幅度波动。经分析可知，PID算法控制下，车身横向倾角最大误差为4.179 9°，平均绝对误差为0.811 1°，均方根误差为1.204 9°；神经网络PID算法控制下，车身横向倾角最大误差为2.874 0°，平均绝对误差为0.577 7°，均方根误差为0.862 1°。可见，基于神经网络PID算法控制的车身横向倾角基本保持水平，满足安全作业的需要，且误差和误差波动程度优于常规的PID控制算法。

图13b为2种算法控制下的摆动机构运动情况。经计算可知，PID算法控制下，左右摆角绝对值差最大误差为5.770 0°，平均绝对误差为1.241 2°，均方根误差为1.546 1°；神经网络PID算法控制下，左右摆角绝对值差最大误差为4.280 0°，平均绝对误差为0.988 5°，均方根误差为1.190 9°。

图13c为基于PID算法和神经网络算法的控制方法下的机具倾角调整效果，可以看出，在150～300 s之间起伏较大的路面行驶时，机具基本可以与路面保持平行。图13d为不同控制算法下机具倾角调整误差曲线，经计算可知，PID算法控制下，机具横向倾角最大误差为2.740 2°，平均绝对误差为0.935 3°，均方根误差为1.360 2°；神经网络PID算法控制下，机具横向倾角最大误差为1.762 0°，平均绝对误差为0.624 6°，均方根误差为0.907 4°。由此可知，相比常规PID控制算法，神经网络PID算法有效提高了机具倾角对路面实际倾角的跟踪精度，降低了误差波动程度，在作业过程中机具基本与路面保持平行，保证了耕深均匀。

由试验数据可知，在起伏较大的随机路面上(路面最大倾角小于15°)，基于神经网络PID算法的同步控制系统效果更好。其中，车身姿态控制方面，车身横向倾角控制精度在±2.874 0°以内，机具姿态控制方面，机具横向倾角与路面倾角差值的控制精度在±1.762 0°以内，在调整车身水平，满足车辆作业安全的前提下，保证了机具横向倾角与路面的平行，从而提高了作业质量和效率。