基于神经网络整定的PID控制变量施药系统设计与试验

孙文峰 刘海洋 王润涛 付天鹏 吕金庆 王福林

(1.东北农业大学工程学院， 哈尔滨 150030； 2.岭南师范学院信息工程学院， 湛江 524048)

0 引言

施用农药是防治病虫草害最为快速、经济、有效的手段。由于植保机械制造及使用水平相对低下，严重影响了植保作业的效果[1-2]。目前，大田施药仍以定量施药方式为主，车辆低速行走时易造成药害残留，车辆高速行走时易造成药液沉积少而无法有效控制病虫草害。因此，农业生产中亟需能随车速变化而相应改变喷量的高效、低污染植保喷雾设备。

变量喷雾是实现精准施药的一种重要技术方式[3]。欧美等发达国家的大田变量施药相关研究开展较早，已经取得长足的进展，相关技术已在市场上推广使用[4-7]。变量喷雾主要通过整合机具速度和管道压力等机器信息、识别田间作物病虫草害和形态等作物信息来实现变量、按需施药。按调节方法变量喷雾可分为浓度调节式、流量调节式和压力控制式[8-12]。ELAISSAOUI等[13]基于电子控制系统设计了一套小型直接注入式喷雾系统，该系统能够有效提高原液利用率，且喷雾状态稳定，但药液浓度改变延时较长。NEEDHAM等[14]研制了一种比例电磁阀控制系统，电磁阀与喷嘴耦合，利用高频(10 kHz)脉宽调制信号占空比改变阀门开度、调节通过药液的流量。PWM式流量调节技术对雾化效果和管道压力影响较小，但高频调节时需要优质高速电磁开关阀支持，低频调节时雾化状态不连续。压力控制式变量喷雾系统主要通过改变喷雾管道的控制阀开度进而实现变量喷雾。孙睿[15]设计了一种基于PID模糊控制理论的压力调控变量喷雾系统，建立了以载体农机动态速度为输入变量、控制阀驱动电压为输出变量的模糊控制规则。但在模糊控制策略下，系统上升时间较长，且稳定性较低。压力调控变量喷雾系统虽然因频繁改变管道压力而影响喷雾均匀度，但该系统具有结构简单、造价低廉、应用性强等优势，因此广泛应用于大田变量喷雾作业中。国内外学者对变量施药的工作原理及应用进行了深入研究，但对现存变量施药控制算法滞后及超调优化方面的研究较少[16-21]。

为提高作业效率和农药利用率，本文设计一种流量自适应的变量施药系统，以调控管路回流量为目的，以神经网络PID控制为实施算法，减少系统滞后时间及超调量，并进行相应田间试验，验证系统可行性和算法优越性。

1 系统组成与设计

1.1 系统结构组成

变量施药系统结构与组成如图1所示。液位传感器安装在药箱底部并与变量喷雾控制器相连，以此监控药箱液位是否在安全范围内。药液受动力输出轴所驱动的隔膜泵作用依次流经主阀、过滤器，高压药液经手动调压阀第1次分流，一部分药液由调压阀流回药液箱，另一部分形成稳定压力的药液经电控调节阀第2次分流，一部分流回药液箱，另一部分依次流经流量传感器、分配阀、压力传感器供给到喷头处，流量传感器与压力传感器分别与变量喷雾控制器相连并实时监测系统的机器信息。本文采用霍尔型速度传感器，获取装备的实时前进速度信息[22]。手动调压阀和电控调节阀开度均可调，其中电控调节阀为变量施药系统的主要执行部件，其安装在回流管路上，接收来自变量喷雾控制器的指令信号，通过改变系统药液回流量进而实现变量施药的工作目标。

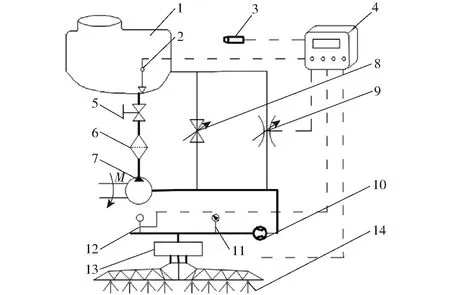
图1 变量施药系统管路结构与组成示意图Fig.1 Schematic of pipeline structure and composition of variable application system1.1000L药液箱 2.投入式液位传感器 3.速度传感器 4.变量喷雾控制器 5.主阀 6.过滤器 7.隔膜泵 8.手动调压阀 9.电控调节阀 10.流量传感器 11.压力表 12.压力传感器 13.分配阀 14.扇形喷头

1.2 电控部分设计

选用的中央控制处理器为STC12C5A60S2型单片机，主要完成对车速、流量、液位、压力信号的处理，对键盘和控制阀的驱动以及控制LCD12864的显示和控制算法运行；选用JK8002C型霍尔速度传感器；选用检测范围为7.5～150 L/min的LWGYA-20型涡轮流量传感器，主要完成对管道流量信号的采集；选用SC-PB800型压力传感器，其检测范围为0～1.6 MPa；采用CBM-2100型投入式静压液位计，其检测范围为0～200 m；设计了LM2596电源转换模块，以保证将车载蓄电池12 V电压转换为稳定的5 V直流电供系统使用；使用4个MOS管设计成H桥电路来驱动电控调节阀内部电机，从而使电控调节阀开度能够按需调控。为采集系统工作信息，基于LabVIEW开发了上位机监测软件，同时调用Excel在采样周期为1 000 ms情况下实时记录机组信息，系统框图如图2所示。

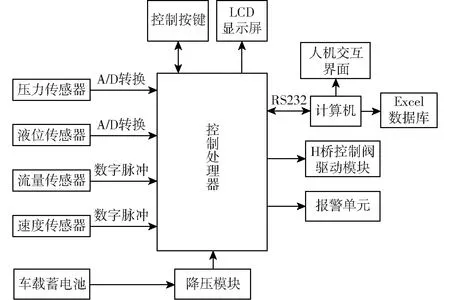
图2 喷雾系统控制原理框图Fig.2 Block diagram of spray system

2 系统控制策略

变量施药系统需实现的技术目标为系统能够根据牵引机具所行进车速而实时调控施药量。因此该系统是以单片机为控制核心，速度传感器输入数据为调控依据，调节阀为执行机构的变量施药系统。

2.1 控制原理

农田施药是一个复杂过程，需要控制的因素较多[23]，本文采用的变量施药方式实质是通过变量喷雾控制器的键盘及显示屏采用人机交互方式预先设置每公顷施药量、喷头数目及喷头间距等参数。工作过程中，控制器通过采集机具行进速度计算出当前所需流量，与流量传感器采集的实时流量数据进行对比计算偏差，将偏差等参数作为系统输入量，通过神经网络PID控制算法修正控制参数，根据计算输出后电压的变化实现阀门开度的调节，改变管路药液回流量，进而使实际施药量与目标理论流量不断接近，达到变量施药目的。目标理论流量与作业速度关系式为

(1)

式中q1——目标理论流量，L/min

C——每公顷施药量，L/hm2

v——行进车速，km/h

d——喷嘴间距，cm

m——喷头数目

由质量守恒可知

q2=Q-q1

(2)

式中q2——目标回流量，L/min

Q——主管路流量，L/min

2.2 主要参数检测

系统以多传感器的检测数据为控制依据，处理器对数据进行分析与计算，并发出相应指令。过程中，通过相应的数学模型对数据计算后推导出相应的作业参数。

2.2.1速度检测

速度传感器安装在拖拉机后轮轴内侧，每有一个金属元件接近时会产生一个脉冲，通过对车轮转动时脉冲计数的方式计算当前车速，其计算式为

(3)

式中r——车轮半径，m

N——后轮轴上金属元件个数

p1——时间间隔t1时系统接收脉冲数

2.2.2液位和压力检测

液位和压力主要为系统提供预警及监测作用且输出均为模拟量，需经A/D将检测的模拟量转换为数字量，为避免药箱内无药液进而导致隔膜泵空转，当药箱液位低于设定值后需进行报警。由于传感器量程与其所输出模拟信号范围呈线性关系，故液位检测值计算式为

(4)

式中H——液位检测值，mm

Hmax——液位测量上限，mm

Hmin——液位测量下限，mm

IWd——液位采样值，mA

IWmin——液位模拟量输出下限，mA

IWmax——液位模拟量输出上限，mA

在实际施药过程中，如果施药系统在流量传感器之后的管路连接处产生破损，由于系统流出药液流量正确，无法得知系统是否存在“漏液”现象；当某些喷头体过滤网处产生“堵塞”现象时，会造成其余喷头流量增大进而导致横向施药不均；上述两种工况发生时仅从流量传感器所传输数值无法知晓，因此系统需要通过压力传感器所传输数据判断管道压力是否在安全范围内，进而判断是否发生上述两种现象。压力检测值计算公式为

(5)

式中p——压力检测值，MPa

pmax——压力测量上限，MPa

IYd——压力采样值，mA

IYmax——压力模拟量输出上限，mA

IYmin——压力模拟量输出下限，mA

2.2.3流量检测

流量传感器输出为脉冲信号，药液流经流量传感器后全部从喷头处流出，故流量传感器所检测数值为实际施药量。所采用的流量传感器内部涡轮在药液作用下旋转，使其内部磁场产生变化，经由放大器作用后输出连续矩形脉冲信号，其计算公式为

(6)

式中q3——实际施药量，L/min

p2——时间间隔t2时系统接收脉冲数

f——流量计系数，取380脉冲/L

2.3 控制器主程序设计

变量喷雾控制采集系统各项参数作为控制依据，利用神经网络PID控制策略进行参数修正。首先系统初始化并进行按键扫描，主要包括端口配置初始化、串口和定时器初始化等，与此同时调用LCD12864液晶显示屏的显示子程序；当选择自动模式后，检测药箱液位是否高于最低值，同时控制器发出指令，电控调节阀进行调节；之后开始检测车辆速度并实现阀门开度的调节；最后将数据发送到上位机储存在Excel数据库中，具体流程如图3所示。

图3 主程序流程图Fig.3 Flow chart of main program

当车速低于4 km/h且不为零时，由于本系统所采用的喷头总成均带有防后滴装置，为保证压力足以顶开防后滴装置的弹簧机构使药液得以雾化，故管路压力应不小于0.1 MPa，需使电控调节阀保持一定开度，因此在系统刚开始启动时电控调节阀处于关闭过程中。在使用36套3号喷嘴的前提下，不同设定施药量与管路最低流量对应关系如表1所示。

表1 不同施药量下管路最低流量Tab.1 Minimum flow rate under different dosages

3 控制算法

常规PID控制存在超调大、干扰后调整时间长、稳态误差较大等问题，并不适用于变量喷雾系统调节，只有调整参数kp、ki、kd，才能取得较优的工作结果。模糊控制虽然可以很好地解决系统的非线性模型问题，但稳定性低及学习能力差的缺点制约其在实际生产中的应用。学习算法和结构简单的BP神经网络已经被广泛应用于PID参数的整定过程中，借助其函数逼近特性及自学习能力不断地修正参数减小偏差，实现控制参数再整定，最终能够取得较好的控制效果[24-29]。

3.1 经典增量式PID控制

采用经典增量式PID控制，其公式为[24]

u(k)=u(k-1)+kp(e(k)-e(k-1))+
kie(k)+kd(e(k)-2e(k-1)+e(k-2))

(7)

式中kp——PID比例控制系数

ki——PID积分控制系数

kd——PID微分控制系数

k——采样序号，k=0，1，2，…

u(k)——第k次采样实际流量，L/min

e(k)——第k次采样流量偏差，L/min

3.2 BP神经网络PID控制算法实现

采用带有动量项的BP网络，通过仿真表明隐含层有5个节点时其表现性能较好，准确度较高。设置输入神经元j=3;隐含层神经元i=5；输出神经元l=3，输入层的输入分别为第k次采样时刻流量偏差、理论流量值、实际流量值，将PID控制器的3个控制系数kp、ki、kd与输出层的3个输出节点相对应，由于3个系数均不能为负数，故输出层选用非负Log-Sigmoid作为激励函数[30]，其学习速率η=0.2，惯性系数α=0.05，权系数初始值选取[-0.5，0.5]内的随机数，控制策略如图4所示。

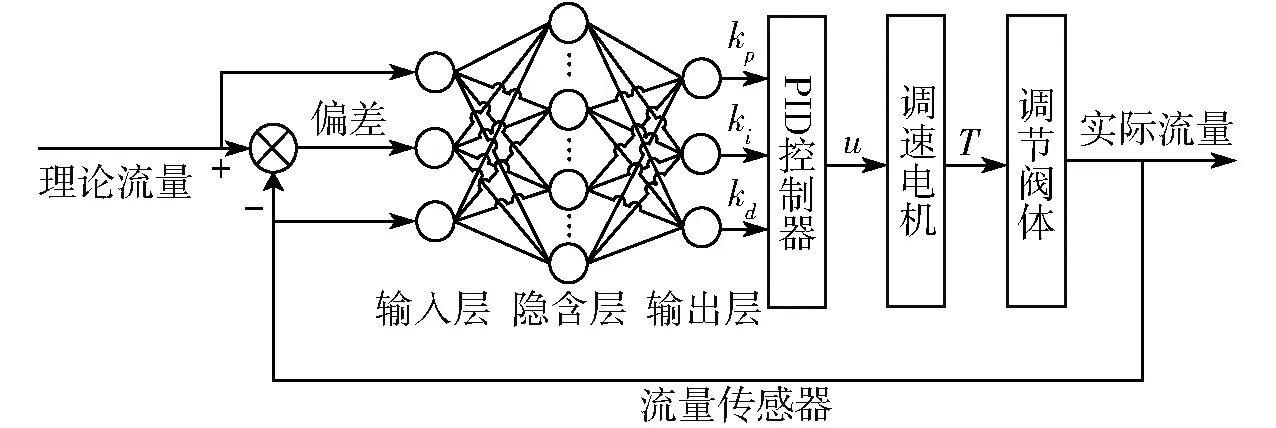
图4 神经网络PID控制策略图Fig.4 NNPID control strategy diagram

图5 BP神经网络PID/模糊PID/常规PID控制系统Fig.5 BP neural network PID/fuzzy PID/traditional PID control system

系统结构输入层的输入为

(8)

隐含层的输入和输出为

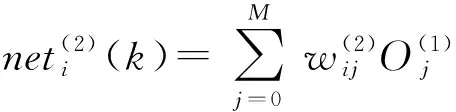
(9)

(10)

隐含层激励函数为

(11)

网络输出层输入和输出为

(12)

(13)

在BP神经网络误差反向传播阶段，为了使输出流量与输入流量之差均值极小，通过系统信号传播所产生的误差可计算网络内各连接权值的更新调整量，通过调整网络加权系数使输出流量无限接近理论流量。

4 仿真与分析

为了验证BP神经网络整定的PID参数控制对于农用喷雾控制的优越性，运用Matlab/Simulink平台引入S函数分别搭建了常规PID控制、模糊控制PID及BP神经网络PID的控制模型，如图5所示，其中对于常规PID控制采用试凑法分别确定其比例、积分和微分参数，通过调整最终确定kp=1.2，ki=0.2，kd=0.8；其中对于模糊控制，采用文献[15]所建立的模糊控制原则对控制模型进行搭建。通过阶跃仿真对3种控制方式进行对比，结果如图6所示。

由表2、图6可知，在阶跃信号作用下，BP-PID决策下系统上升时间为0.25 s，超调量为1.30%，稳态误差为±0.26%。模糊控制PID上升时间为0.64 s，超调量为18.2%，稳态误差为±0.94%。常规PID控制上升时间为0.30 s，超调量为50.9%，稳态误差为±1.21%。综上所述，BP神经网络PID控制在阶跃响应上超调量较少、上升时间较短、稳态误差较小。通过仿真可知，BP-PID控制在所搭建的控制模型下能够较好地解决常规PID存在超调量大、模糊PID存在滞后的问题，并能够取得较好的响应效果。

5 田间试验

试验于2020年7月14—18日在东北农业大学种植基地进行，试验地为马铃薯垄作地，以水为试验介质，由于本次试验需使用水敏纸(日本AS ONE)探究使用变量喷雾控制系统的液滴沉积效果，应避免田间相对湿度及叶片呼吸作用对本试验的影响。故雾滴沉积效果探究试验时间选在14:00—15:00，试验时空气相对湿度为68%，环境温度为27℃。喷雾装置为3WF-1000型悬挂式喷雾机，配有1 000 L药液箱、MB390/3.0型隔膜泵、TEEJET AIXR11003型喷嘴(36套)、液压折叠系统、幅宽18 m桁架，牵引机具为约翰迪尔904拖拉机，施药控制器为自主研制的PW-01型变量喷雾控制器，如图7所示。

图6 阶跃跟随曲线Fig.6 Step following graph

表2 阶跃响应结果对比Tab.2 Comparison of step response results

图7 田间性能试验Fig.7 Field performance experiment

试验参考GB/T 20183.3—2006《植保机械 喷雾装置 农业液力喷雾机每公顷施液量调节系统试验方法》，标准要求试验时行进车速为5.4～9 km/h。考虑到田间实际作业是在外界条件多胁迫情况下进行，并且田间实际工作时在启车及驻车阶段(车速较低时)均会进行施药作业，故本试验行进速度范围在国家标准基础上有一定延伸，最低速度设为0 km/h；同时由于本系统选择3号喷嘴，在施药量为150 L/hm2情况下，为保证喷嘴工作压力不高于0.4 MPa(喷嘴优选的工作压力)[31]，以延长其使用寿命及保证喷雾作业横向均匀性，试验最高速度设为11 km/h(喷嘴压力为0.4 MPa)，故行进速度范围为0～11 km/h。

5.1 动态流量跟随对比试验

为更好验证所设计的BP-PID变量施药系统在实际作业中的实时调控优越性，采用车速随机变化的方式来验证BP-PID变量施药系统与模糊PID变量喷雾系统的动态跟随性，模糊PID控制系统采用课题组自行研发并已在市场推广使用的变量施药系统[15]。设定需求喷雾量150 L/hm2，驾驶员操控拖拉机使车速在4～11 km/h范围内随机变化，拖拉机启动后首先打开动力输出轴进行喷雾作业，当车速到达4 km/h后开启变量喷雾控制器进行施药量调节并记录；通过控制油门缓慢增速达到11 km/h后逐渐减速至4 km/h时停止施药；变量喷雾控制器通过RS232串行通信接口与便携式计算机相连，通过上位机监测软件实时计算并记录当前车速、压力、理论流量及实际流量。通过曲线形式在上位机展示并实时记录储存在Excel数据库中，模糊PID控制下试验结果如图8所示，BP-PID控制下试验结果如图9所示。

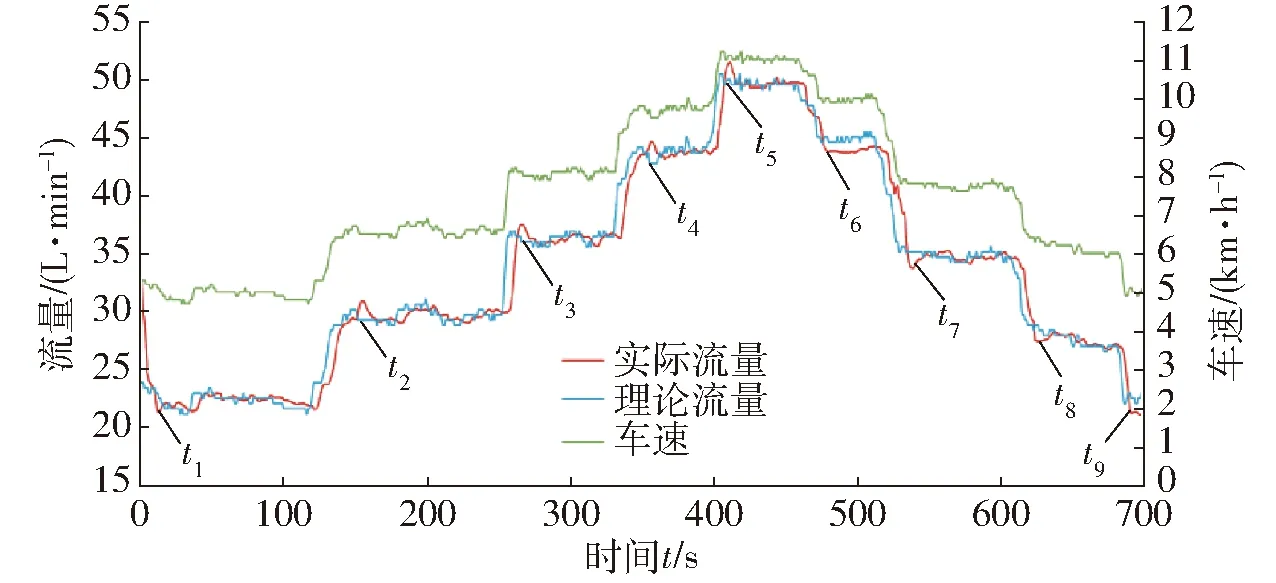
图8 模糊PID控制动态跟随流量、速度响应曲线Fig.8 Dynamic follow flow and velocity response curves of fuzzy PID control

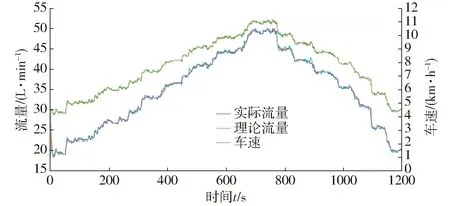
图9 BP-PID控制动态跟随流量、速度响应曲线Fig.9 BP-PID control dynamic follow flow and velocity response curves

由图8可知，变量施药系统采用模糊控制策略会产生1～4 s的滞后；在时刻t2、t3、t4、t5，由于车速增加，喷雾量跟随产生上升超调，在时间段t2～t5内平均施药量为157.3 L/hm2，在时刻t1、t6、t7、t8、t9由于系统启动或车速下降，喷雾量跟随产生下降超调，在时间段t6～t9内平均施药量为134.8 L/hm2；整个喷雾过程共喷洒394.5 L，由于增速和减速而产生的超调量为17.6%，平均调整时间为2.54 s；利用Excel软件统计试验实测施药量为142.1 L/hm2，与理论值相差5.9%。

由图9可知，变量施药系统采用BP-PID控制策略，流量跟随紧密，解决了模糊PID控制存在的超调及滞后问题；整个喷雾过程共喷洒752.3 L，平均超调量为2.1%，平均调整时间为0.72 s；统计试验实测施药量为151.9 L/hm2，与理论值相差1.3%。

5.2 流量控制精度和纵向施药均匀度试验

5.2.1流量控制精度试验

目前我国大部分地区茎叶处理施药量为100～150 L/hm2，试验前设置施药量为100、125、150 L/hm2。为验证所设计的BP-PID变量施药系统在设定施药量情况下的流量控制精度，首先切换至手动调节模式并采用给定速度试验方式屏蔽车速传感器，给定系统车速分别为6、7、8 km/h，在流量显示值稳定后记录数据；随后系统切换至自动调节模式，车辆田间试验时在车速0～11 km/h范围内随机变化，当液位低于设定下限，控制器报警后停止试验，其试验结果如表3所示。由表3可知，在进行速度给定试验时，系统实现了“高速多喷，低速少喷”的作业目标。且由于拖拉机未在田间行走,降低了施药量误差，在速度和设定施药量各水平组合试验下，试验误差均不大于2%。在进行田间行走试验时，流量随着车速的不断改变而变化，由于试验是在田间多因素胁迫下进行，所以产生误差较大，但系统总体误差仍稳定在3%以内。该系统可实现根据车速调节流量的变量喷雾作业目标，且控制精度较高，适用于大田作业。

5.2.2纵向施药均匀度试验

提升现有施药方式纵向(机组行进方向)施药均匀度是本文的主要目标。选取表3中控制器处于自动调节模式下的9组试验数据作为BP-PID控制决策施药系统的样本来源，同时采用模糊PID控制决策下的施药系统进行对比试验，每组重复3次。以机组每行进5 m所喷洒区域(90 m2)施药量作为计算数值，以此探究所设计变量施药系统的纵向施药均匀度。部分喷洒区域施药量如表4所示。

表3 喷雾试验结果Tab.3 Spray test results

表4 纵向施药均匀度试验结果Tab.4 Longitudinal application uniformity test results

由表4可知，BP-PID控制决策下的施药系统在整个施药作业过程中，施药控制误差最小为-4.5%～14%，控制精度较差，而当工作过程中车速大于等于4 km/h时，施药控制误差稳定在-5%～5%之间，控制精度较好，由于当车速低于4 km/h时，为保证管路压力足以顶开防后滴装置进行喷雾作业，从而使此区域施药量较高(0～5 m区域启车阶段、3 215～3 220 m区域驻车阶段)；当工作过程中车速大于等于4 km/h时，计算不同设定施药量各喷洒区域施药量变异系数均小于6%，且组间平均值为5.1%。对于模糊PID控制决策下的施药系统，当工作过程中车速大于等于4 km/h时，施药控制误差最小为-6.3%～7.4%；当工作过程中车速大于等于4 km/h时，计算不同设定施药量各喷洒区域施药量变异系数最小值为6.9%，且组间平均值为8.1%，相较采用BP-PID控制决策下的施药系统高3个百分点，原因是由于模糊PID控制在实际工作中产生的超调及滞后。综上所述，说明本文所设计的变量施药系统的纵向施药均匀度较好，性能稳定。

5.3 雾滴沉积性能试验

将水敏纸均固定在植株上端叶片，为避免由于采集时间过长而造成水敏纸局部甚至整张变色，同时为减少试验误差，各个车速下随机设置6个水敏纸取样区域，每个取样区域面积为1 m2，区域间隔保持5 m以上，各取样区域内采用五点取样法选取5株植株作为取样点，将水敏纸使用订书器固定在叶片上。在田间设置车速区段提示物及车速变化缓冲带，经过提示物时驾驶员操纵手动油门适时增速或减速。为了便于数据分析，取因素水平分别为5、6、7、8、9、10 km/h。喷雾机作业后取下水敏纸，带回实验室进行分析，试验取每平方厘米雾滴沉积数为试验指标，将每个取样区域内5个取样点水敏纸雾滴沉积数量统计并取平均值作为该取样区域数值进行分析。每个车速下取样区域序号为1、2、3、4、5、6[32-33]。采用样条插值法绘制车速动态变化下液滴沉积数量如图10所示。

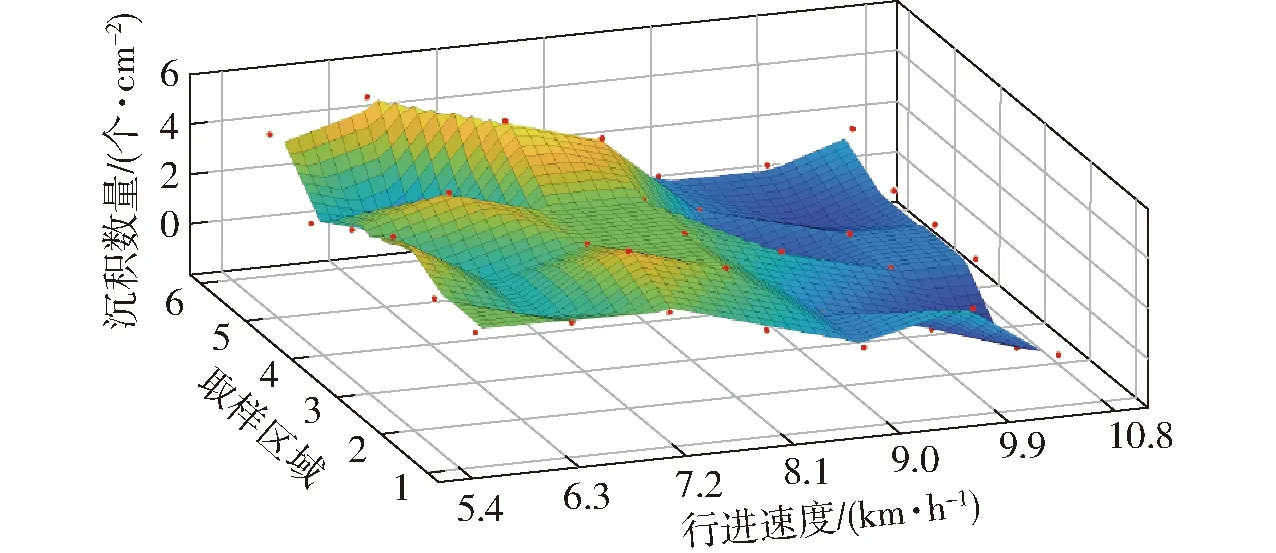
图10 车速动态变化下液滴沉积数量Fig.10 Droplet deposition under dynamic change of vehicle speed

采用文献[34]的计算方法，取各车速下液滴沉积数量平均值作为对比数据。随着车速不断增加，液滴沉积数量呈减少趋势，原因可能是由于压力增加后液滴粒径尺寸变小，并且拖拉机高速行驶时后方流场作用和相对风速增加而加剧了飘移，但极差为3.1个/cm2，表明数据变化浮动不大。变量喷雾系统在车速变化时药液沉积数量较稳定。

对每个车速下的各取样点计算雾滴沉积数量标准差。由图11可知，随着车速增加，雾滴沉积数量标准差并无明显变化趋势，均小于1.4个/cm2。说明变量喷雾系统在各个车速下雾滴沉积数量较稳定，并无明显差异。

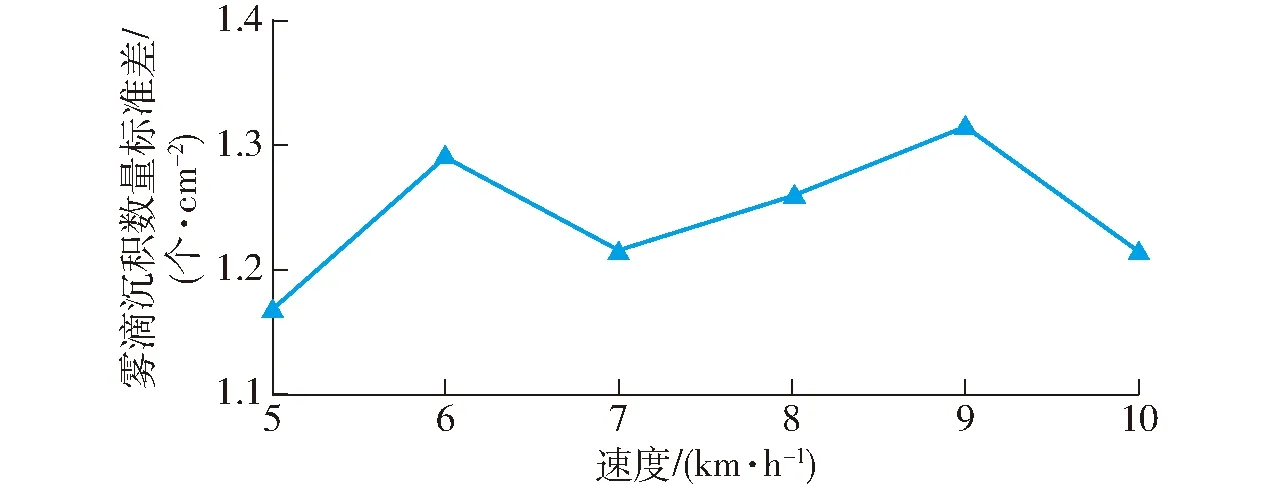
图11 各车速下雾滴沉积数量标准差Fig.11 Standard deviation curve of droplet deposition number at different speeds

图12为喷雾作业后沉积效果，国家标准要求进行防虫或防病喷雾作业时，作物上沉积液滴数量最低为30个/cm2。结合试验数据分析，本系统工作时单位面积最低沉积数量为38个，作业效果高于国家标准[31]。综上所述，采用本文设计的变量喷雾施药方式下液滴沉积密度符合国家标准，其变异系数低，适用于大田作业。

图12 喷雾作业后水敏纸液滴沉积效果Fig.12 Water-sensitive paper droplet deposition after spray operation

6 结论

(1)针对常规大田定量喷雾方式下容易产生药害残留及少喷的情况，同时为了提高现有变量喷雾控制系统的时效性，解决模糊决策的滞后性问题，设计了BP神经网络PID变量喷雾系统。

(2)运用Matlab分别对3种控制策略进行建模仿真，结果表明，基于BP-PID控制的上升时间、超调量、稳态误差分别为0.25 s、1.30%、±0.26%，明显优于其他2种常规控制方式。

(3)在马铃薯大田中分别进行了神经网络PID变量喷雾系统的动态流量跟随试验、流量控制精度试验、纵向施药均匀度试验和沉积性能试验。当车速在4～11 km/h范围内随机变化时，试验实测喷雾量为151.9 L/hm2，与理论值相差1.3%，系统平均调节时间为0.72 s，平均超调量为2.1%；在进行田间行走试验时，施药控制误差稳定在3%以内；当车速大于等于4 km/h时，施药量控制误差稳定在-5%～5%之间，且变异系数均小于6%；各速度下雾滴沉积数量标准差均小于1.4个/cm2，且雾滴沉积数量高于国家标准。说明所设计变量施药系统纵向施药均匀度较好、性能稳定。