基于矩阵分解和层次聚类的协同过滤推荐算法

东苗 王启宗

（1.上海行健职业学院 上海市 2000722 2.北京红亚华宇科技有限公司 北京市 102209）

1 引言

随着信息技术、大数据技术和人工智能的快速发展，个性化推荐技术已经渗透到社会的各个方面，如音乐、电影、短视频、图书、广告、旅游、电商等领域。在海量信息中能否快速找到最有价值的信息，最重要的环节是个性化推荐系统的核心即推荐算法。推荐算法主要有基于知识的推荐算法、基于内容的推荐算法、协同过滤算法等，目前应用范围最广且效果较好的推荐算法是协同过滤算法，协同过滤算法利用用户的相似性来推荐用户感兴趣的信息，但由于协同过滤算法存在冷启动、数据稀疏和可靠性不高的问题，导致推荐精准度不高。

针对上述问题，本文提出一种基于矩阵分解和层次聚类的协同过滤推荐算法。通过矩阵分解将原评分稀疏矩阵进行降维分解得到两个低秩矩阵，数据填充得到不含缺省值的完整评分矩阵。再对样本训练集上的用户构建层次聚类模型进行分类划分。在协同过滤阶段，对测试集中的用户首先在聚类模型中找到该用户所在的聚类，再在该聚类中进行最近邻集选取、预测评分、选取TOP-N、生成列表、产生推荐。[1]

2 协同过滤推荐算法

协同过滤算法一般可以分为三个步骤：[2]

step1.构建“用户-项目”评分矩阵。定义矩阵Rm×n表示表示m 位用户对n 个项目的评分数据。

度量用户相似度的方法主要有：余弦相似度（Cosine Similarity）、Pearson 相关系数（Pearson Correlation Coefficient）和修正余弦相似度（Adjusted Cosine Similarity）。

（1）余弦相似度：把用户对项目的评价看作一个n 维向量，两个用户间的相似度通过二者向量夹角的余弦来度量。设用户i 和用户j 的评分分别用向量Ii和向量Ij表示，可计算两者间的余弦相似度sim(i,j)：

（2）Pearson 相关系数：皮尔森相关系数对变量进行均值化处理，降低了变量个体数值差异带来的影响。设用户i 和用户j 共同评分的项目用集合Hij表示，则两者间的相似度sim(i,j)可表示为：

其中，ri,c和rj,c分别表示用户i 和用户j 对项目c 的评分，与分别表示用户i 和用户j 对各项目的平均评分。

图1：矩阵分解模型

图2：AHC 流程图

图3：算法流程

（3）修正余弦相似度：余弦相似度未考虑到用户不同的评价尺度问题，修正余弦相似度通过减去用户对项目的平均评分来改善用户评分的差异。设Hi和Hj分别表示用户i 和用户j 评分的项目集合，则两者间的相似度sim(i,j)可表示为：

分别统计N(i)中的用户对不同项目的兴趣度的加权平均值，取其中N 个排在最前面且不属于Hi（Hi表示用户i 评分的项目集合）的项作为Top - N 推荐集。

传统的协同过滤算法主要依赖于“用户-项目”评分矩阵。但在实际应用中评分矩阵往往是极其稀疏的，导致无法计算相似度或精度不高，找到的最近邻不可靠，最终的推荐效果不理想。[3]

3 基于层次聚类和矩阵分解的协同过滤推荐算法

针对传统协同过滤算法中存在的问题，本文提出基于层次聚类和矩阵分解的协同过滤推荐算法。首先通过矩阵分解模型对“用户-项目”评分矩阵进行降维处理，矩阵填充以降低矩阵的稀疏性；再通过层次聚类对用户属性划簇，以减少最近邻的搜索范围并增强其可靠性；最后进行协同过滤推荐。

3.1 矩阵分解模型

矩阵分解思想最初来源于信息检索领域的隐语义索引（Latent Semantic Indexing,LSI）方法，LSI 使用了奇异值分解（Singular Value Decomposition,SVD）算法对“文档-词”矩阵进行分解。[4]但是SVD 应用到推荐系统领域会存在对稀疏评分矩阵的预测不准确、可扩展性低的问题。矩阵分解（Matrix Factorization,MF）算法借鉴了SVD 的思想，通过对“用户-项目”评分矩阵进行分解得到隐空间来分别表示用户和物品。矩阵分解的数学表示如图1所示。

在m 个用户和n 个项目的评分矩阵Rm×n中，可将有评分的项设为1，无评分的项设为0。通常该交互矩阵是非常稀疏的。矩阵分解模型将高维的评分矩阵分解为低秩的用户隐含信息矩阵Pm×k和项目隐含信息矩阵Qk×n，两个低秩矩阵构造的预测矩阵相乘尽可能地逼近原评分矩阵Rm×n。用户对项目的喜好程度的预测值 可以表示为：

将TOP-N 推荐问题转化为最小二乘问题求解：

输出：P,Q

（5）for count in 1 to iters:

（6）for ＜user,item,rating＞ in T:

3.2 层次聚类

层次聚类(Hierarchical Clustering)属于无监督学习的一种聚类算法，通过对原始数据集在不同的层次进行划分，直到达到某种条件为止，最后得到树形的聚类结构。按照分类原理的不同，可以分为凝聚式层次聚类(AHC)和分裂式层次聚类(DHC)，其中凝聚式的应用比较广泛。[5]首先将原始数据集中的每个样本都单独作为一个簇，原始的类中心为然后分别计算两个簇之间的距离，按照相似度从高到低排序依次合并成簇，直到达到预先设定的聚类数目或者相似度阈值为止。如图2所示。

本文采用Average Linkage 聚类法计算Ci和Cj两簇间的距离式中|p-p'|表示样本p 和p'之间的距离，ni和nj分别表示簇Ci和Cj中样本数。

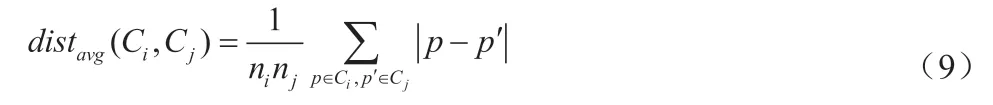
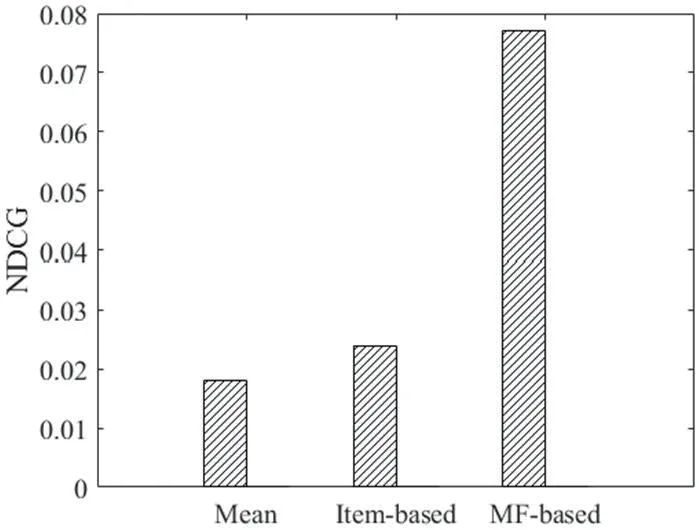
图4：不同算法下的NDCG

图5：不同算法下的RMSE

3.3 基于层次聚类和矩阵分解的协同过滤推荐算法

基于层次聚类和矩阵分解的协同过滤推荐算法将层次聚类与矩阵分解模型相结合，可以使结果更加准确。算法主要包括矩阵分解、层次聚类和协同推荐三个阶段。

（1）通过矩阵分解将原“用户-项目”评分稀疏矩阵分解成两个低秩矩阵Pm×k和Qk×n，对P 和Q 分别进行迭代，使两个低秩矩阵构造的预测矩阵相乘尽可能地逼近原评分矩阵Rm×n；通过R=PQT得到不含缺省值的完整评分矩阵；

（2）根据得到的用户矩阵，通过层次聚类对用户进行划分，最后形成k 个聚类，；

（3）协同过滤：由于已经通过层次聚类将相似的用户划分为一个簇，当测试集中的用户加入到系统中时计算该用户与各簇中心点的距离，将其划到距离最近的簇中并从该簇中选取N 个相似度较高的用户作为其最近邻居集，通过式（5）进行预测打分后选取评分位于前列的N 个项目，生成最终的列表TOP-N 返回给该用户，算法流程如图3所示。

4 算法的测试和评价

4.1 数据集

本文实验基于2 个数据集。第一个数据集是电影评分历史数据集，包含105,339 个样本。第二个数据集是电影信息数据集，由美国运输局收集整理，包含10,329 个样本。

4.2 评价指标

本文中采用两种方式对推荐算法进行评估。第一种是由推荐算法预测每个用户评分最高的前k 个电影列表，与该用户实际评分的电影做对比，计算根据排名加权的重合度。第二种是由推荐算法预测每个用户已评分的电影的评分，与真实值做对比计算误差。

（1）归一化衰减累积增益（NDCG）

归一化衰减累积增益定义为：

其中，L 是按推荐评分降序排列的电影列表，Lideal是按用户真实评分降序排列的电影列表，u 是用户，i 是排名，rui是用户u 对排在第i 位电影的评分。

（2）均方根误差（Root Mean Square Error,RMSE）

均方根误差通过计算预测评分与实际评分之间误差的均方根来衡量推荐结果的准确度，RMSE 越小，说明推荐的精度越高。假设预测的用户评分集合表示为对应的实际用户评分集合为则均方根误差RMSE 定义为：

4.3 测试流程

4.3.1 数据预处理

将数据集分为5 组训练集和测试集做5 折交叉验证。在推荐系统中分割训练集和测试集时按照用户做分割，具体方法为：

step1.将用户分割成5 组测试集用户；

step2.对于每组测试集用户，再进一步抽取这些用户20%的评分样本作为测试集；

step3.创建对应的训练集，包含该组测试集用户得其余80%的评分样本以及所有非测试集用户的评分样本。

4.3.2 候选推荐数据准备

合并所有的测试集，为后续模型性能评估做准备。在给用户做电影推荐时，需要提供一个候选推荐列表。数据集中有部分电影只有极少数的评分，因此并不稳定，这里排除所有评分少于5 条的电影。

4.4 实验结果分析

为与传统的推荐算法进行对比，本文选取基于个性化平均评分的推荐和基于电影相似度的协同过滤推荐做对照实验。绘制3 种推荐算法用于推荐列表的NDCG。可以看出，基于个性化平均评分的推荐最差，基于矩阵分解的协同过滤推荐最好。如图4所示。

绘制3 种推荐算法用于预测评分的均方根误差。可以看出，基于个性化平均评分的推荐最差，基于矩阵分解的协同过滤推荐最好。如图5所示。

5 结束语

综上所述，为了避免由于评分矩阵数据稀疏、高维度带来的计算误差及协同过滤过程中带来大量的数据冗余，提高推荐算法的效率和精度，本文提出了一种基于层次聚类和矩阵分解的协同过滤算法。首先利用矩阵分解技术对评分矩阵进行降维及数据填充，减少了由于数据稀疏性带来的推荐误差；然后使用分解得到的用户矩阵，利用层次聚类算法对用户进行聚类划分，最后进行协同过滤处理，根据项目评分预测产生TOP-N 推荐列表。对比实验结果验证了该算法的准确度和有效性明显优于传统协同过滤推荐算法。