基于FPGA的最佳精度定点加法器的设计与实现
2020-02-01黄政凯刘冰洋翟明明罗二平刘娟
黄政凯 刘冰洋 翟明明 罗二平 刘娟
(空军军医大学军事生物医学工程学系 陕西省西安市 710032)
FPGA 技术作为ASIC 专用集成电路领域中的一种半定制电路而出现,一方面解决了定制电路的不足,另一方面克服了原有可编程器件门电路数有限的缺点,是在PAL、GAL、GPLD 等技术基础上进一步发展的产物。我们知道,FPGA 技术可将DSP 的性能提升至最大化,且传统处理器的性能增长趋势放缓,因此该技术在DSP领域的应用越来越普及[1]。利用FPGA 领先的并行机制可实现DSP的架构功能,这种并行机制可以完成类似“滤波”这样重复性的DSP 任务。因此,对于执行高度并行的DSP 任务来说,FPGA 技术的处理速度要远高于DSP 处理器的处理速度,而且其性能也远远超过通用DSP 处理器的串行执行架构[2-3]。
加法器是数字计算系统中的基本逻辑器件,也是其他所有硬件运算的基础,减法器和乘法器都可由加法器来实现,大大地节省了逻辑资源。我们知道,设计宽位的加法器耗费硬件资源相对多一些,因此,在系统的具体设计与实现过程中需要重点考虑“资源的利用率”和“速度”这两方面的因素。基于此,首先选择合适的目标器件,一般会考虑FPGA、CPLD 等较为合适的组合逻辑设计的器件;其次,结合加法器逻辑结构的设计、加法器的处理速度及芯片资源的利用率等方面,来探究最佳组合[4]。本文主要介绍了16 位最佳精度定点加法器的硬件实现方法,采用VHDL 语言,在一般的FPGA 上,实现了定点加法运算功能,并总结其优缺点,进行代码优化。
1 设计思想
为了提高芯片的利用率,节省硬件资源,并扩大输入数据的范围,根据“保持最佳精度的定点数运算法则”对算法进行代码优化,设计出算法性能更好的最佳精度定点加法器。
首先,可以通过把小数点位置定标为数量级来解决输入定点数的数值范围小的问题,此时的q 值可正可负,这种标定小数点位置的方法极大地扩展了输入定点数的数值范围。
其次,具体提出“输入和输出位宽均定义为16 位”及“采用节拍(时钟)来控制移位操作”这两种解决方案,来提高芯片利用率,从而节省硬件资源。
方案具体设计如下:
令dq=aq-bq,根据dq 的值分为表1所示的三种情况。
另外,由于输出的位宽定义为16 位,如果两个16 位二进制数的最高位都为‘1’,则相加结果就为17 位,为防止计算溢出,可以尝试在算法中定义17 位的中间变量,在输入前补一个‘0’赋给中间变量,再进行加法操作。这样进行加法运算所得的和为17 位,而输出定义又为16 位,为了解决这个问题,具体可按表2所示方法处理。
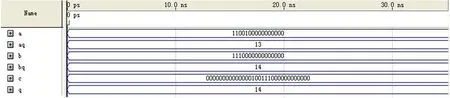
图1:仿真结果6.25+3.5=9.75

图2:仿真结果1.5+1.75=3.25
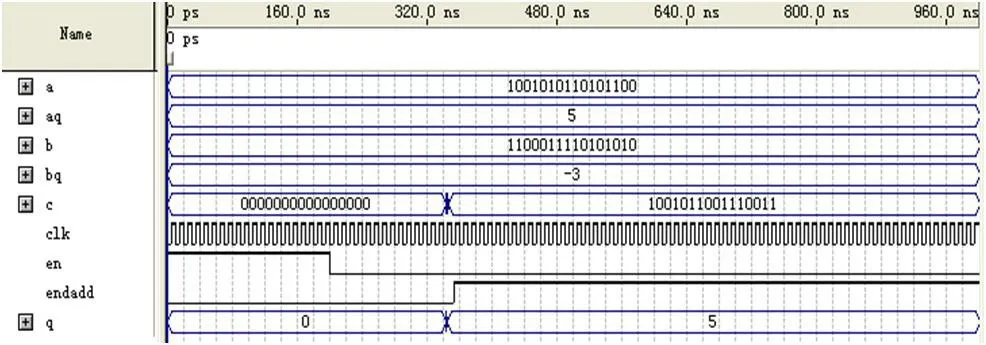
图3:仿真结果1226112+6389.25=1232480 (1232501.25)
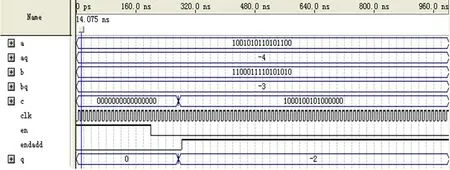
图4:仿真结果2394.75+6389.25=8784 (8784)
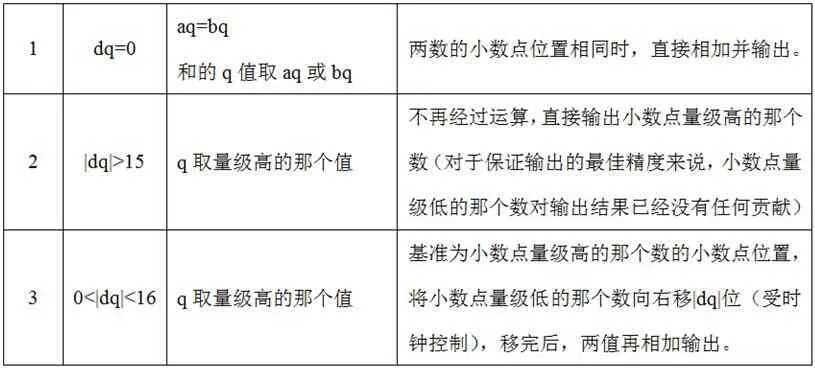
表1

表2
这种处理方法不仅可以保证硬件加法器16 位的位宽输出,达到了节约硬件资源的目的,也可以确保输出数据的最佳精度,因此我们把其称为“16 位最佳精度加法器”。
2 仿真验证
为验证所设计的加法器,选取几组数据对其进行仿真。等号后的值为在保证数值最佳精度的情况下的计算结果,括号内的值为保持全精度的计算结果。图1、图2、图3、图4 是其中的部分仿真图。
3 结论
从运算开始到运算结束的时间最长在220ns 左右,此时间是由移动的位数来决定的,相对来说速度很高,虽然输出位宽控制在16位,但是保证了输出结果的最佳精度,避免了由于数据溢出导致的运算精度的严重恶化。该算法由于采用数量级来标定小数点的位置扩大了定点数的输入范围,采用时钟控制移位并限制了输入和输出的位宽,大大节省了硬件资源,共使用182 个逻辑门,比上一种方法减少了419 个的使用量,提高了芯片的利用率。
4 讨论
该算法采用VHDL 语言中的状态机实现了两个定点数的相加运算,并给出最终输出的小数点位置,代码结构简单、思路清晰,且该算法可以扩展到任意位数,可以说是在加法器逻辑结构的设计上,在加法器的处理速度、运算精度及芯片资源的利用率等方面权衡得失的一种最佳算法。
