微电网中主电源逆变器控制算法

刘国联

（湖南铁路科技职业技术学院 湖南省株洲市 412000）

近年来，我国微电网发展迅速，在多个地区铺设，成为人们日常生活和工作不可缺少的一部分[1]。为了保证微电网得以长期稳定运行，构建储能系统是当前重点开展工作。主电源是储能系统的核心，电源逆变器在很大程度上决定了供电质量[2-3]。以往提出的主电源逆变器控制算法不满足独立控制要求，电压控制偏差较大。为了弥补传统控制算法存在的不足，本文引入电流内环双闭环、电压外环控制方法，提出新的算法研究。

1 微电网中主电源逆变器拓扑结构

离网型三相逆变器在微电网供电中应用较多，本文选择该设备作为研究对象，依据拓扑结构及工作原理，提出控制算法。逆变器电感、电阻等零件采用星形连接方式组建而成。其中，L 代表逆变器的交流侧电感，L0代表逆变器的负载侧电感，两者对应的寄生电阻依次为R、R0。假设此类型逆变器在作业过程中三相负载皆处于平衡状态，将输出电流数值作为逆变器的扰动输入参数数值，能够生成关于交流侧电压的传递函数，利用此函数可以得出逆变器作业期间的谐振状态信息。

2 主电源逆变器控制算法

2.1 双闭环控制结构框架设计

本文针对离网型逆变器控制需求，将电流内环双闭环、电压外环控制方法植入逆变器控制体系中，形成双闭环控制结构，其框架设计方案如图1所示。

图1 中，逆变器双闭环控制结构由外环控制器、内环控制器、控制对象3 部分组成，本系统的双闭环体现在外环控制结构和内环控制结构两个方面。

2.2 电感电流反馈内环控制

本文提出的双闭环控制结构中，利用电压外环控制逆变器的输出电压，该控制体系不支持电流直接控制。为了实现电流直接控制，本控制体系增加了电感电流反馈内环控制结构，成为了双闭环控制结构。离网型逆变器作业期间滤波器谐振现象较为频繁，通过布设内环控制体系，可以很好的抑制谐振。关于内环控制的传递函数为：

公式（1）中，s 代表拉普拉斯运算符。按照公式（1）中的内环控制关系，计算谐振频率和阻尼系数，分别为。

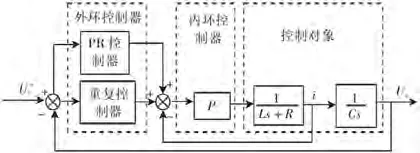
图1：双闭环控制结构框架设计

在原有逆变器控制体系结构基础上，添加内环控制模块以后，电感寄生电阻中加入了新的电阻P，使得逆变器系统阻尼系数得以增加，相比于改变前，运行稳定性更强。

2.3 复合控制电压外环函数

本文提出的电压外环控制模块是一种复合结构，支持重复控制，在闭环重复控制体系中，能够根据逆变器所处作业环境情况，做出实时调控方案，以此消除特殊情况下电压偏差，使得逆变器控制精准度更高。

“粮食银行”破解了农民储粮、卖粮难题，也减轻了运营主体的资金压力。原粮供应多了，对企业来说粮源也稳定了。

重复控制技术建立在内模控制基础上，通过扰动处理，重复多次对信号进行修正，使得输出信号得以更加准确的还原。在本文研究的主电源逆变器控制算法中，重复控制技术用于消除控制体系中生成的非线性负载扰动信号，使得输出电压波形与实际波形更加贴合。

本文提出的重复控制器分为前馈和反馈两部分，借助低通滤波器减弱高频积分，通过合理设置比例阐述，以此有效限定系统积分，提高系统运行稳定性，使其更加有效地控制逆变器，实现主电源灵活控制。以下为重复控制技术下的电压外环函数：

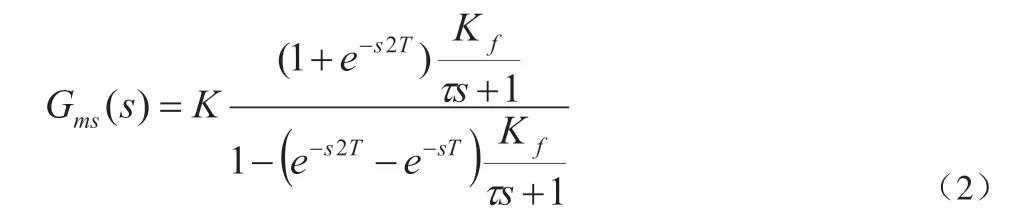
公式（2）中，τ 代表低通滤波器作业时间；K 代表控制结构的比例常数；T 代表主电网基波周期；Kf代表控制结构反馈和前馈系统。

为了实现零误差信号跟踪，提高谐振点增益，本文在公式（2）函数基础上，采取“无静差”处理方法，以提高信号跟踪精准度。目前，“无静差”处理方法较为成熟，此处不做过多介绍，得到重复控制传递函数：

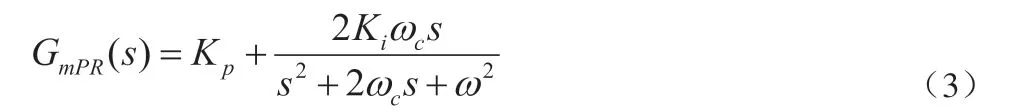
公式（3）中，Kp代表控制结构比例常数；ω 代表基波角频率；Ki代表积分常数；ωc代表截止频率。

与未改变前，PR 控制器对系统增加带宽帮助较大。当微电网作业频率发生小幅度变化时，本文提出的逆变器控制系统不会发生较大变化。

3 主电源逆变器控制函数详细设计

3.1 内环控制与复合控制函数

依据前文提出的内环控制函数和复合控制函数，设计开环传递函数：

对应的闭环函数为：

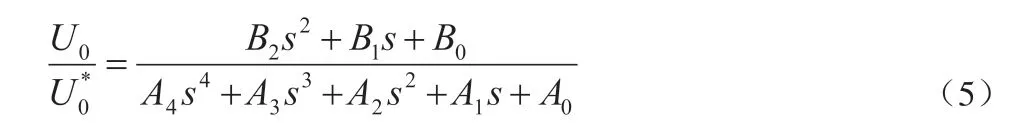
通过求取特征方程，按照劳斯判据，得到各个参数之间的关系。按照此关系确定主电源逆变器参数。本文以P、Ki、ωc、Kp依次为2.49、10、15、0.039 这组数据为例，分析闭环传递函数零极点分布情况。根据函数点分布情况可知，所有点均分布在圆内部。因此，本文提出控制函数运行得到的数据较为稳定，符合逆变器控制需求。

3.2 重复控制传递函数及控制条件

另外，本文提出的改进算法还增加了重复控制模块，包括反馈环节和前馈环节。关于控制函数功能的实现，以Kf、τ、K3 个参数为主要设计参数，根据控制需求拟定设置方案。

（1）τ 参数的设置。该参数值的设定与低通滤波器作业效果密切相关，通过限定此数值，削弱高频积分。考虑到低通滤波器截止频率参数值不得高于电路高频谐振点数值，本文研究的三相逆变器中低通滤波器中此参数的最小值为500Hz，依据各项参数之间的关系，取时间数值τ 数值为3.18×10-4。

（2）Kf参数的设置。该参数的设置与系统谐振波动性能密切相关，依据反馈和前馈两个环节控制器连接方式，分析谐振频率及峰值变化情况。当系统加入内环控制模块后，产生的谐振波形将随之发生变化。当Kf数值减小时，系统频率波动适应性逐渐增强。所以，根据系统抗谐振波动需求，即谐振带宽和增益参数数值控制范围需求，合理设置Kf数值。

（3）K 参数的设置。该项参数的设置与控制器累加处理功能密切相关，当系统稳定性提高时，系统静差就会随之增加，如何控制二者之间的关系成为了算法研究的关键。通常情况下，K 参数取值不得高于1，在满足系统运行稳定条件下，调整K 数值，要求该数值为基波频率的整数倍。对于本文研究的逆变器重复控制体系，此参数的设置等效于系统谐振，为了保证系统运行稳定性，综合考虑内环控制要求和外环控制要求，设计开环控制函数：

依据小增益定理，分析公式（6）不等关系，得出一个关于K参数值的不等式：

综合考虑公式（6）和公式（7）关系，得出系统得以稳定运行的充分条件：

4 测试分析

4.1 测试内容

本文选取PR 控制器应用下的闭环控制算法作为对照组，本文提出的改进控制算法为实验组，通过对比两种算法在模拟应用中的电压偏差、电压谐波抑制情况得出相应结论。

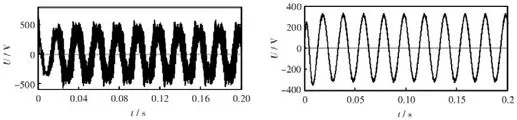
图2：电流内环控制应用前后电压波形对比结果

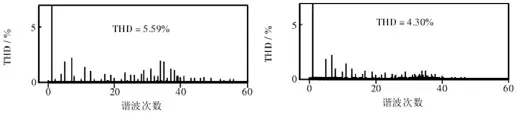
图3：重复控制下的外环控制电压谐波失真对比结果

4.2 测试结果分析

按照测试内容要求，本研究对PR 控制器闭环控制算法和本文提出改进算法应用下的逆变器输出电压偏差进行测试。

测量时间为0.3s ～0.45s 范围时，对照组和实验组的电压偏差较大，其他时间产生的电压偏差较小，实验组应用的控制算法优势显著。因此，本文提出的改进控制算法得到的输出电压偏差更小，达到了改善传统控制算法的目的。

另外，本文分别对改进控制算法的两个闭环控制体系作用进行测试，结果如图2 和图3所示。

图2 中，左侧图为未使用电流内环控制的电压波形，右侧图为使用电流内环控制的电压波形。对比左侧图和右侧图可知，改进算法中的电流内环控制体系的应用，能够有效控控制电压，使其按照微电网供电需求，对逆变器进行有效操控。

图3 中，左侧图为未使用外环控制的电压谐波测试结果，右侧图为使用外环控制的电压谐波测试结果。对比左侧图和右侧图可知，改进算法中的外环重复控制能够起到抑制谐波失真的作用，较未使用时降低了2.29%干扰率。

5 总结

本文围绕微电网中主电源逆变器控制问题展开研究，通过分析传统控制算法应用中存在的问题，引入双闭环控制思路，提出改进算法。此算法主要由电感电流反馈内环控制函数、复合控制电压外环函数两部分组成，分别起到降低电压偏差和抑制谐波作用。测试结果表明，本文提出的改进算法不仅可以有效降低电压偏差幅度，而且还能够抑制电压谐波，避免电压谐波失真，影响逆变器控制效果。