一种基于PCA降维的SIFT算法

肖璞，殷一鸣

（三江学院计算机科学与工程学院，南京210012）

0 引言

人脸识别是生物特征识别技术中重要的研究领域。由于脸部图像采集过程中情绪和环境的变化，如多姿态的表情、光照强度的变化、噪声强度的变化、旋转、缩放尺度、人脸上的遮挡物（眼镜、太阳镜、帽子、伤口敷料等）、年龄变化等，准确而强大的人脸识别系统面临着巨大的挑战。SIFT算法基于尺度空间上图像潜在的对尺度和选择不变的兴趣点，与图像的大小、尺度缩放、旋转都无关。该算法对于光照强度的变化、噪声强度的变化以及微视角变化的容忍度相当高，保持了一定程度的稳定性。然而，SIFT算法的缺点也不容忽视。该算法具有高维度，每个特征点包含128维特征描述符，计算量很大。计算复杂度高，计算过程繁琐，严重影响了人脸识别的实时性。经典的SIFT算法的计算量很大，每一个特征点都包含有4×4×8=128个特征描述向量，在细节复杂的区域提取过多的特征点容易产生误匹配，针对目标跟踪的实时性，SIFT算法的效率极低。

本文提出了一种改进的基于PCA降维的SIFT算法，在SIFT算法的原有基础上利用降维方法来降低维度，简化计算复杂性和计算繁琐的过程，提高人脸识别的效率。改进的SIFT算法相比原有的SIFT算法有着明显的优越性，在保持原算法的光照不变性，旋转不变性，尺度缩放不变性和遮挡不变性的同时，可以加快海量数据的处理速度。

1 改进的PCA-SIFT算法

1.1 SIFT算法

人脸识别系统大致分为以下四个阶段：人脸图像采集及检测、人脸图像预处理、人脸图像特征提取、人脸图像匹配与识别[1]。其中，人脸图像特征提取是人脸识别过程中至关重要的一步。特征提取不仅提取输入图像中最有用的特征，而且还大大降低了图案样本的维度。输入的人脸图像的特征点数量很多，所构建的尺度空间维数也很高，通过对人脸图像的提取以获得最有用的人脸特征，也达到了将尺度空间从高维降到了低维[2]。而人脸图像特征提取的方法有尺度不变特征变换算法（SIFT）[3]等。人脸图像匹配与识别是人脸识别流程的最后一步，最常用的相似度匹配算法是欧氏距离（Euclidean Distance），因为它具有明确的物理意义，良好的聚类效果，容易实现的特点[4]。

尺度空间理论[5]的提出最早可追溯到1962年。SIFT算法是一些基于尺度空间上图像潜在的对尺度和选择不变的兴趣点，与图像的大小、尺度缩放、旋转都无关。同时，SIFT算法对于光照强度的变化、噪声强度的变化以及微视角变化的容忍度相当高，保持了一定程度的稳定性。使用SIFT特征算法对于遮挡的人脸的侦测率也相当得高，仅仅是需要3个以上的SIFT人脸特征就能够识别检测出人脸。此外，SIFT算法独特且信息丰富，可以在海量特征库中快速准确地匹配。

国内外的研究学者针对SIFT算法提出了许多改进算法。林晓帆等人提出了基于SURF描述子的遥感图像配准[6]，经过改进的SURF发算法极大地提高了效率，但该算法只是侧重于遥感图像的配准。芮挺等人提出了基于SIFT描述的Harris角点多源图像配准[7]，也提高了匹配效率，提升了精度；张少敏等人提出了融合SIFT特征的熵图估计医学图像非刚性匹配[8]，将医学图像配准改进的具有良好的鲁棒性，该算法也只是侧重于医学图像配准[9]。有许多学者提出了不同的改进方法，都有取得一定的成果，但也有一定的局限性。

1.2 PCA降维技术

在处理图像时，为了提高准确率，一般会提取较多的特征点或是一些较为复杂的特征点，每个特征点又会生成128维的特征描述子。为了改进SIFT算法这种特性，需要对其引入降维技术处理，将120维的特征向量降维64维，甚至是32维的特征向量。

PCA作为一种线性降维技术，它将许多相关输入特征的样本作为输入，并输出作为输入特征的线性组合的正交特征。也就是说将高维的原始图像通过投影的方法映射到低维的空间中，并希望尽可能多地保留原始图像的像素点，去除带有比较少量信息的像素点。映射后数据的方差越大，保留的原始图像的特征点越多。

PCA算法的核心是找到最大方差。设W是投影矩阵，则图像x在新坐标里的投影是WTx，方差为WTxxTW，目标函数为：

再使用拉格朗日公式对公式（13）求解，得：

其中-λ是XXT的特征值，要想把图像从n维降到k维，需要k个特征值对应的特征向量，由k个特征向量组成的矩阵W[10]。

研究证明，PCA是丢失原始图像的像素点最少的一种线性降维技术。LDA算法也是一种比较经典的线性降维方法，但它有一个基本前提自变量是正态分布的。本文利用PCA降维技术对SIFT算法进行降维处理。

1.3 改进的PCA-SIFT算法

虽然，SIFT算法应用于人脸识别中解决了图像的旋转、尺度缩放、光照变化、噪声干扰等问题，但由于存在高维（128维）的特征向量，使得计算复杂度较高，识别过程所需要的时间较长，实时性不高。为解决这一问题，本文提出了一种基于PCA降维的SIFT算法，利用对特征点具有筛选功能的PCA算法，将SIFT算法事先提取出来的特征点进行筛选过滤，把高维数据投影到低维空间中，去除冗余的特征点，从而改变了生成特征描述子的方式，达到降维的效果。生成PCA-SIFT描述子的流程图如图1所示。

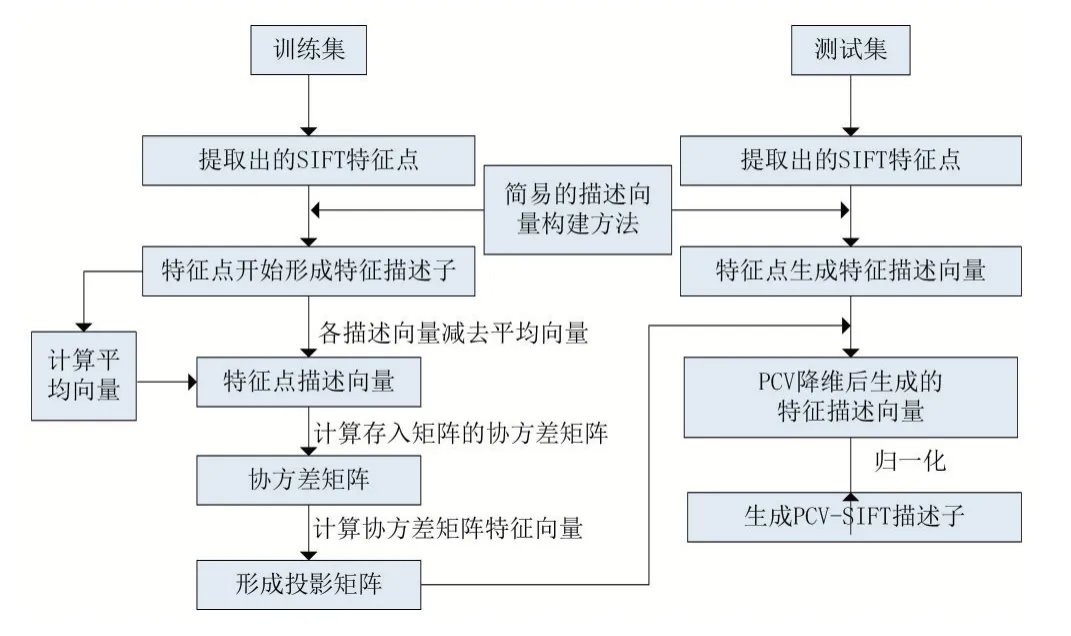
图1 生成PCA-SIFT描述子的流程图

计算PCA-SIFT投影矩阵的算法描述如下：

（1）利用SIFT算法将训练集中的特征点提取出，个数记为n。

（2）对每一个特征点在开始生成特征描述子的时候，划分一个41×41的邻域窗口，并将坐标轴旋转至特征点主方向。去除四个角的边缘像素，计算剩余每个像素在水平和竖直方向上的梯度，得到39×39×2=3042的描述向量。

（3）计算n个特征点的3042维描述向量的平均向量，并且用n个特征点的3042维向量减去平均向量，将得到的差值放入n×3042的矩阵W中。

（4）计算矩阵W的协方差矩阵CovW，并计算协方差矩阵CovW的特征值和特征向量。

（5）将获得的特征值从大到小进行排序，选择前k个特征值对应的特征向量作为主成分方向，从而组成k×3042的投影矩阵。其中k为PCA-SIFT特征描述子的维数。

生成PCA-SIFT特征描述子的算法步骤如下：

（1）将坐标轴旋转至特征点的主方向，划分一个41×41的邻域窗口，并计算去除边缘角点像素后的每个像素在水平和竖直方向上的梯度，即得到一个39×39×2=3042维的描述向量。

（2）利用上一节求得的投影矩阵乘以该向量，得到一个k维的特征向量。

2 PCA-SIFT算法实现

2.1 ORL人脸数据库

ORL人脸数据库是由英国剑桥大学AT&T实验室创建的，里面包含有40个人，每人10张不同表情、姿态或含有不同程度遮挡物的灰度图像。图片的尺寸均为92×112。这是目前研究人脸识别使用最多的人脸数据库之一。

2.2 算法实现

（1）SIFT算法的实现步骤如下：

Step1：构建DOG差分尺度空间。

Step2：构造高斯金字塔。

Step3：使用DOG来代替LOG，用差分代替微分。

Step4：构建DOG金字塔。

Step5：寻找关键点。

Step6：关键点精确定位。

Step7：删除边缘效应。

Step8：方向赋值：根据检测到的关键点的局部图像结构为特征点方向赋值。

（2）PCA算法不同维度的比较。

①首先定义PCA算法。

Step1：对列求平均值。

Step2：将所有样例减去对应均值得到A。

Step3：获取协方差矩阵。

Step4：求协方差矩阵的特征值和特征向量。

Step5：按列取前r个特征向量。

Step6：小矩阵特征向量向大矩阵特征向量过渡。

Step7：循环对特征向量归一化。

②训练PCA算法。

分别降维到40、30、20和10时的准确率如图2所示。

图2 不同维数的识别准确率的综合图

本文中我们选择k=20，也就是说会把SIFT的128维特征描述子降到20维的PCA-SIFT特征描述子[11]。

3 实验对比与分析

针对不同表情、姿态的变化、遮挡物，比例缩放等因素的影响，以下四组实验展现了效果，如表1所示。

表1 实验效果比较表

根据实验结果对SIFT算法和PCA-SIFT两种算法进行比较，如表2所示。

表2 SIFT算法和改进的PCA-SIFT算法的优缺点比较表

SIFT算法和PCA-SIFT两种算法运算时间的比较如表3所示。

表3 SIFT算法和改进的PCA-SIFT算法运算时间比较表

综上所述，改进的PCA-SIFT算法在效率上明显优于SIFT算法，提高了算法的计算速度。

4 结语

本文基于PCA降维技术对SIFT算法进行了改进，完成了以下工作：

（1）阐述了改进的PCA-SIFT算法的原理，改变了生成描述子的方式。

（2）通过实验实现了PCA-SIFT算法，并通过ORL人脸数据库的人脸数据验证了PCA-SIFT算法的优越性。在研究过程中，本文选择了将维度降为20进行对比研究。比较了SIFT算法和PCA-SIFT算法下不同维度的运行情况。从而可以发现不同的维度对应的准确率不同。维度越低，准确率就越低。

本文在多姿态人脸识别中对SIFT算法进行了研究，通过对其优化和改进取得了一定的进展，但在研究过程中也遇到了一些瓶颈和问题。如实验数据样本的选取，维度的选取如何界定等。特别是如何提高降维之后的准确率，这在后期的工作中仍需进一步的探讨和研究。