水星表层构造及其成因研究进展

2020-01-18谢景椿黄乘利

天文学进展 2019年4期

谢景椿，黄乘利，张冕

(1.上海科技大学物质科学与技术学院，上海201210；2.中国科学院行星科学重点实验室，上海200030；3.中国科学院大学天文与空间科学学院，北京100049)

1 引言

人类对水星的研究主要通过地基探测和空间探测两种方式。早在水星探测器升空之前，人们就已经通过地基雷达探测并确定了水星的自转周期及其处于3 : 2 轨道共振状态等一系列特性[1,2]。由于水星距离太阳很近，其周围的空间环境复杂且恶劣，来自太阳的巨大引力使得探测器进入水星轨道时，人们需对其进行复杂的变轨操作。也是因为上述原因，任何想要飞临水星的探测器不得不面对上百度的高温，并需防范潜在的空间环境效应，因此，从水星探测器的设计，到它的发射和入轨都困难重重。正因如此，水星是人类造访次数最少的太阳系内行星之一，目前只有水手10 号(Mariner 10)和信使号(MESSENGER)成功地对水星进行过探测[3]。由欧空局(European Space Agency, ESA)与日本宇宙航空研究开发机构(Japan Aerospace Exploration Agency, JAXA)联合研制的贝皮·科伦布号(BepiColombo)已于2018 年10 月20 日被成功发射，预计将在2025 年进入水星轨道，成为第三颗造访水星的人造卫星。

水手10 号于1973 年被发射。由于技术原因，该探测器仅在1974 年和1975 年在水星表面进行了三次飞越式探测。水手10 号上搭载了近红外辐射测量仪、大气-掩星紫外光谱仪、磁力计、成像仪，以及带电粒子和等离子体探测仪[3]。水手10 号在飞越水星期间，共拍摄约2.3×103张照片。人们通过该探测器取得了多项科学成果，如首次发现水星具有与地球类似的偶极磁场[4]。

信使号于2004 年被发射，并于2011 年3 月进入绕水星的轨道。2015 年信使号以受控撞击的方式撞向水星表面而结束其探测任务。信使号搭载了激光高度计、γ 射线-中子探测仪、X 射线光谱仪、磁力计、水星大气和表层成分光谱仪、双成像系统，以及高能粒子和等离子体光谱仪[3]。信使号在轨10 a，飞行距离达1.2×1010km，共向地球传回了超过2.5×105张图片，约10 TB 的科学数据。人们通过信使号取得了令人瞩目的成果，如成功绘制了水星全球地形图[5,6]，测定了水星表面主要化学元素的丰度[7,8]。

贝皮·科伦布号是一种复合式探测器，由水星轨道环绕器(Mercury Planetary Orbiter,MPO)和水星磁层环绕器(Mercury Magnetospheric Orbiter, MMO)组成。MPO 携带了激光高度计、综合成像设备、γ 射线-中子探测仪、辐射计与热成像光谱仪、磁力计、弹簧加速度计、成像X 射线光谱仪、无线电科学试验设备、中性-带电粒子分析仪、(太阳)X 射线-粒子光谱仪以及水星外大气层探测仪。MMO 则携带了等离子体探测仪、等离子体波探测仪、水星大气钠光谱成像仪和水星尘埃检测仪[9]。

尽管水手10 号和信使号的成功极大地促进了人类对水星的了解，但这只是揭开了水星神秘面纱的一角。这个怪异的星球依旧困扰着研究者们，水星畸高的密度之谜、偶极磁场形成之谜等一系列问题仍都悬而未决[10−12]。如今，全球水星研究者们的目光都聚焦于贝皮·科伦布号，希望能够通过它进一步撩开水星神秘的面纱。研究水星不仅可以为我们了解太阳系类地行星的形成和演化提供帮助，也将极大地促进深空探测技术的发展。另外，水星还是研究系外类地行星的一个很合适的样本。

本文介绍了与水星表层构造相关的热点问题及研究进展，包括发育于水星表层的主要地质构造与水星径向收缩的关系，水星表面主要地质构造的走向、分布和成因，以及对水星的壳层热结构和水星地壳厚度的研究现状。

2 水星的主要地质构造和径向收缩

水星的径向收缩是其热历史的重要反映。从水星径向收缩的程度，能够直接或间接地反演水星的演化过程，从而为研究水星地幔对流和水星磁场产生机制等一系列问题提供重要帮助[13−17]。

水手10 号和信使号的探测结果表明，水星表面遍布着多种多样的地质构造，它们大致可以分为皱纹脊(wrinkle ridge)、叶状悬崖(lobate scarp)及高凸浮脊(high-relief ridge)三类(见图1)。它们被认为是由于水星收缩所导致的岩石圈形变而产生的[13,14,17]。

皱纹脊(如图1a)所示)是典型的宽、低起伏的拱形构造，由褶皱和冲断层组合而成，其长度多在100 km 以内，且地形起伏较小，最高处大多不超过1 km[14,15]。叶状悬崖(如图1b)所示)是一种线状或弧状构造，其长度可从几十千米延伸至上百千米。从平面上看，叶状悬崖地势起伏多变，最高处可达几千米，其地形剖面展现出正面坡陡，背面舒缓的特征。目前已知最长的叶状悬崖名为企业悬崖(Enterprise Rupes)，它的长度接近1 000 km，最高处可达3 km[14,15]。高凸浮脊(如图1c)所示)一般可以延伸至几百千米长，但是由于其宽度较大，所以在影像上不容易被识别。与皱纹脊和叶状悬崖不同，高凸浮脊典型的地形剖面图呈中间高，两边对称下降的趋势，被它们穿过的撞击坑呈现破裂或变形构造，这一构造被解释为是由逆断层形成的[14,15]。目前，在水星表面的部分区域已经发现高凸浮脊向叶状悬崖转变的证据，它们共同组成了水星上最长的地质构造[15]。

图1 水星表面三种主要的地质构造[14]

叶状悬崖是水星表面最常见的地质构造，一直以来被用于分析和研究水星内部结构、地质活动史及其热演化历史[13,15,18]。由于叶状悬崖被解释为水星收缩形成的冲断层所导致的地表破坏，因此，Watters 等人[19]提出了弹性位错模型，认为可以将断层产生的水平收缩距离作为断层倾角和断层滑动位移的函数(见图2)。他们据此模型研究了水星的径向收缩，并给出了相关定义：

其中，S表示水平收缩距离，h表示起伏，D表示断层最大滑动位移，θ表示断层倾角，µ表示摩擦系数。

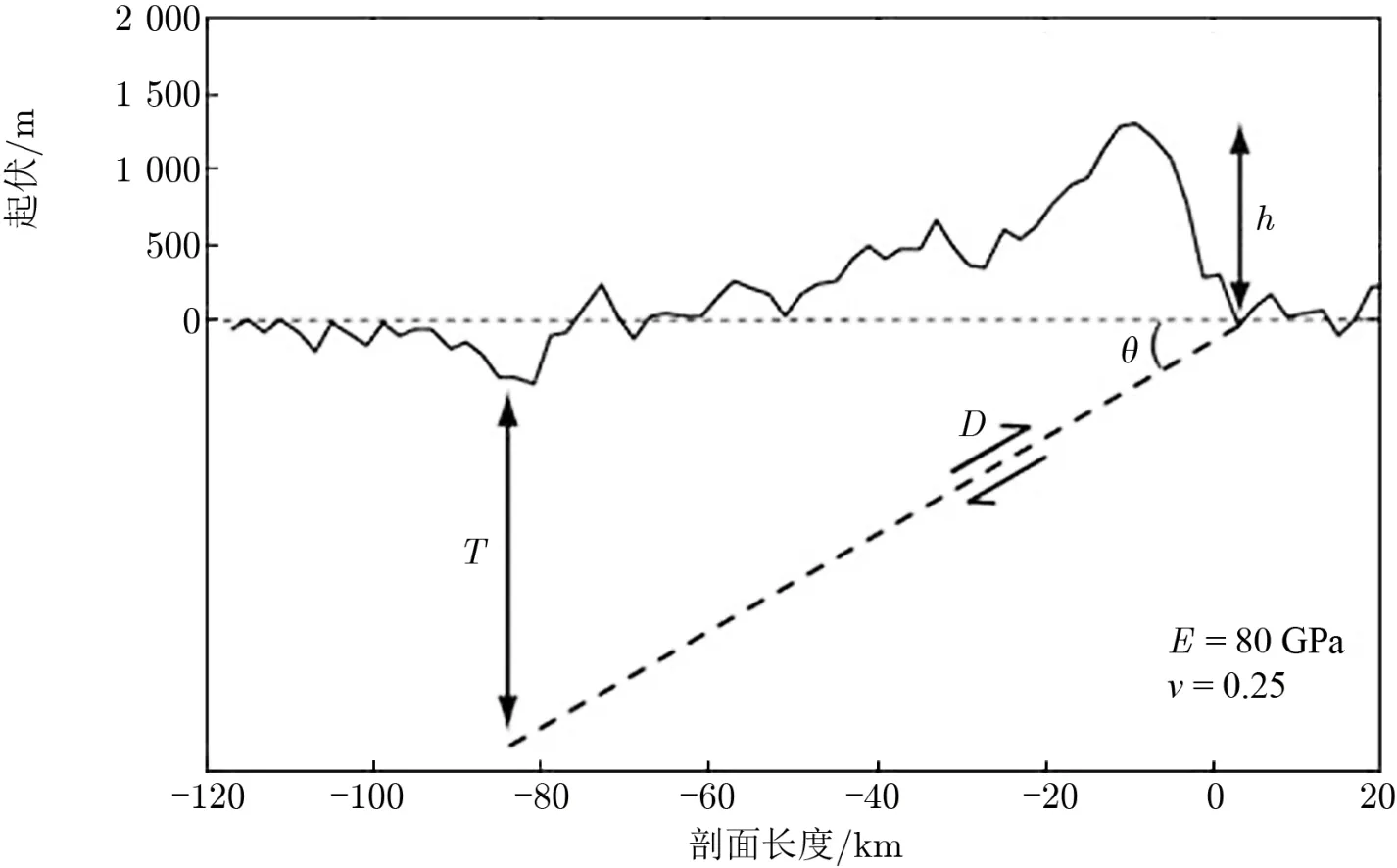
图2 弹性位错模型示意图[19]

该模型使用叶状悬崖的起伏h来估算断层的最大滑动位移。用同样的方法还可以计算出水平收缩距离。从以上公式不难看出，要研究径向收缩，需要较精确地确定断层倾角θ的值。式(3)阐述了断层倾角与摩擦系数的关系。由实验室测定的典型摩擦系数为0.6∼0.8，一般认为最佳取值为0.65[20−22]。Sato[23]开发了一种基于应力张量反演技术的计算机算法来计算摩擦系数。在应用了一系列天然断层的数据后，他计算出的摩擦系数约为0.7。而根据弹性位错模型，以及由实验室测定的典型摩擦系数，他计算出所对应的断层倾角约为25◦∼30◦。考虑到Brewer 等人[24]对地球上类似断层的研究结果，Watters 等人[19]将断层倾角拓展至20◦∼35◦。

对断层的研究发现，断层最大滑动位移Dmax与断层的位移长度标尺(displacementlength scaling, DLS)L有关。如果岩石类型较为单一，那么一般有Dmax/L=γ。该比值γ与岩石类型和构造背景有关[25,26]，对于地球而言，经典γ值的量级为10−3∼1[27−29]。Schultz 等人[30]研究了表面重力加速度对于DLS 的影响，认为太阳系类地行星的γ值最多只有地球的1/5。Kling 和Klimczak[31]计算了火星上29 个冲断层的DLS，得出γ值为0.037，为10−2量级，与Hauber 等人[32]和Polit 等人[33]的结果类似。Li 等人[34]计算了月球上近百个皱纹脊所对应的γ值，其范围是1.73×10−2∼2.13×10−2，与Roggon 等人[35]的0.023接近。

对于水星而言，水星断层的DLS 可以直接用叶状悬崖的长度代替。Watters 等人[19]选择水星表面典型的叶状悬崖，计算出γ值为6×10−3∼8×10−3，其所对应的断层倾角为25◦∼35◦。Byrne 等人[15]用水星上216 条收缩构造，计算出γ值为7.1×10−3∼9.6×10−3。因此，根据上述结论，一般可以认为典型的叶状悬崖所对应断层倾角为20◦∼35◦。事实上，不少研究工作中已经采纳了该范围[15,36−39]。由于弹性位错模型一般选择某些独立的叶状悬崖作为研究对象，适用的范围是局域性的，所以一般将局域的水平收缩量转换为由于收缩导致的局域表面积减少量。这样做的好处就是可以将计算的局域收缩量外推至水星全球，以计算全球的收缩程度。目前，这已经成为一种较为通行的做法[19,36,40]。但是这种方法也存在明显的缺陷，即将局域结果外推实际上隐含着岩石圈受力均匀的假设，因此，想要获得更加有说服力的结论，就需要对水星表面全球分布的构造进行识别。Byrne 等人[15]分析了信使号在轨3 a 所探测的地表数据，并结合长波段地形数据，在水星全球范围内识别出了超过5×103条叶状悬崖和皱纹脊，最终得出了水星径向收缩最多达7 km 的结论。

尽管通过上述方法研究水星径向收缩程度存在一定缺陷，但这是一种直接且操作性很强的方法，因此被广泛采用。另外，人们常常利用水星径向收缩量为构建水星热演化模型提供约束。这类模型的经典切入点就是研究热能从水星由内向外运输的过程。一般方法是将水星划分为不同的层状结构，比如地壳、地幔、液核以及固态内核，并分别给出热能在不同结构中的传输方程，即一系列微分方程，然后通过求解微分方程[16,41−43]，得到水星内部各层的温度/热流随时间或深度的变化。此外，还可以通过将诸如材料的热膨胀系数等参数与由于温度变化所导致的体积变化相联系，进而预测径向收缩量，并与通过地质构造的研究所得出的结论进行比较，然后反向修订热演化中的模型参数，从而得到更符合真实情况的温度/热流变化，并在此基础上研究水星地幔对流、地壳增生等问题。如果再结合重力测量、天平动幅度等数据，还可为构建水星内部结构模型提供约束，得到内核半径大小等信息，并在一定程度上还原水星形成早期核幔分异等过程，从而帮助人们理解水星早期的演化历史[16,42,43]。

3 叶状悬崖的走向和分布

通过研究水手10 号传回的数据，Melosh 和Mckinnon[44]发现叶状悬崖大多表现为南北走向(N-S orientation)。Watters 等人[45]通过分析信使号所获得的全球分布的构造数据(如图3a)所示)，得出了叶状悬崖不光表现出特定走向，还呈现出不均匀分布的结论，具体表现为：在低纬度到中纬度之间，叶状悬崖大多为南北走向；而在高纬度地区，则大多为东西走向(E-W orientation)，并在经度为110◦,−30◦,−90◦附近呈条带状聚集(如图3b)所示)。

不仅如此，叶状悬崖的数量和长度在南北半球也存在明显差异：大多数长的叶状悬崖都集中在南半球，其累积长度是北半球的3 倍(如图3c)所示)。如果这只是受到水星收缩的影响，那么产生的收缩应力应使叶状悬崖的走向和分布表现出随机性[14]。因此，Melosh 和Mckinnon[44]提出，潮汐可能会影响水星断层的发育，进而影响叶状陡崖的走向。在此基础上，Dombard 和Hauck[46]构建出了一个拥有薄的弹性壳层的岩石星球潮汐应力模型：

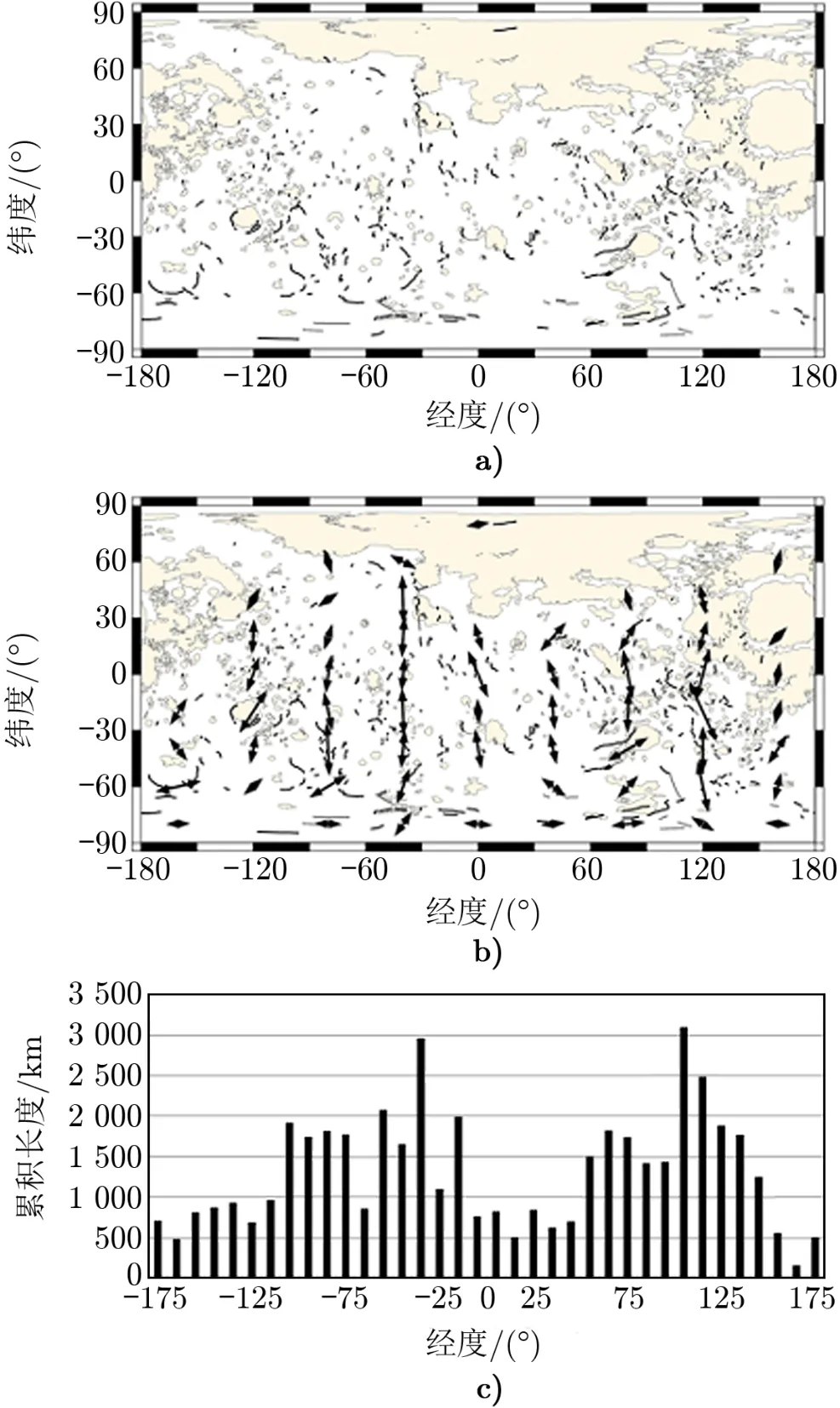
图3 叶状悬崖的走向和分布[45]

其中，σlongitude表示经度方向上的应力，σlatitude表示纬度方向上的应力，φ表示纬度，Ω1表示形成初期的初角速度，Ω2表示当下的末角速度，∆表示赤道上初、末向心加速度与重力加速度的比值，G表示万有引力常数，M表示星球质量。

通过该模型可以计算出，两极地区应力大小相同，但东西向的应力大于南北向的应力。这会导致在极区高纬度地区产生东西走向的正断层，而在中纬度和低纬度地区，如果再施加一个全球性的均匀的应力(如收缩应力)，那么其合力将会使得纵向应力大于横向应力，从而产生南北走向的冲断层[45,46]。尽管由该模型得出的低-中纬度的南北走向冲断层与实际观测结果相符，但是Dombard 和Hauck[46]的结论却与观测到的高纬度东西走向的冲断层相矛盾。由于水星具有非常小的轨道倾角，以及非常高的轨道偏心率，同时它处于3 : 2 轨道共振状态，即每自转3 周完成2 周公转[1,2,47,48]，因此，当水星处于近日点时，太阳直射点(即热极)在经度0◦和180◦，而在远日点时，太阳直射点(即暖极)在经度90◦和270◦。水星在近日点和远日点所接收的太阳辐射量的差异可达40%，最终使得热极和暖极的平均温度差为100∼130 K[49,50]。Williams 等人[49]认为，该较大的温差会导致岩石圈结构和强度发生变化，并在全球收缩应力和潮汐的共同作用下，影响冲断层的发育。尽管用水星全球收缩观点，并结合潮汐以及日照模式，可以对南北走向和东西走向冲断层的发育给出较为合理的解释，但是却不能解释叶状悬崖在经度−30◦和110◦(如图3b)所示)呈条带状聚集这一现象[45]。James 等人[6]用地形和重力数据进行双重反演，分析了水星北半球大型的叶状悬崖的位置与地壳厚度的关系，发现这些大型的叶状悬崖多数聚集在地壳较厚的地区。基于Neil和Houseman[51]关于地球上板块内部的地幔下沉是导致地壳增厚和岩石圈压缩应力局部化的一种机制的研究结果，Selvans 等人[52]提出，地幔下沉可能是导致叶状悬崖在特定区域聚集的原因。尽管目前人们已提出多种多样的理论，但是仍没有找到一种或多种机制能同时解释叶状悬崖的走向和分布之谜[45]。不难发现，对叶状悬崖的走向和分布的研究，有助于揭示水星岩石圈的受力状态，并为研究与之相关的岩石圈物质组成和流变特征等提供新的契机。

4 水星壳层热结构

叶状悬崖和皱纹脊被认为都是由水星逐渐冷却过程中形成的冲断层所导致的地质构造，因此，我们可以利用它们来研究水星壳层热结构。这不仅有助于了解水星早期的地幔分异历史，也能为研究水星地幔对流等热动力学过程提供帮助[13−16]。

一般来说，由于类地行星表层温度相对较低，在非流体静平衡压的作用下，浅层岩石被破坏的模式主要是脆性破裂。随着深度的增加，温度逐渐升高，岩石圈的变形模式逐渐过渡到韧性变形。这个由脆性破裂向韧性变形过渡的区域被称为脆-韧转化带(brittle-ductile transition, BDT)。在韧性变形的模式下，岩石很难积累应变能量，因此弹性应变能集中在温度较低的浅层区域。当积累的能量达到一定程度时，就可能诱发地震或造成岩石圈破裂，从而形成断层[23,53−55]。因此，可以认为断层发育的最大深度就是岩石圈发生脆性破裂时的最大深度，即脆- 韧转化带的最大深度[53]。Watts[56]和Scholz[21]给出了岩石脆性应力和韧性应力的表达式：

其中，σbrittle表示脆性应力，σductile表示韧性应力，ρ表示密度，g表示重力加速度，z表示深度，表示应变率(即应变随时间的变化率)，A和n表示与介质有关的常数，Q表示活化能，R表示气体常数，T(z)表示温度。

第2 章中已经提到，摩擦系数µ可由实验室测定，一般情况下可选择0.65 作为最佳值。另外，人们发现类地行星板块内部典型的应变率量级为10−19∼10−16s−1[22,57,58]。Zuber 等人[40]认为，10−17s−1是适用于水星的应变率上限值。Egea-Gonzlez 等人[38]在研究中采用10−16s−1和10−19s−1作为应变率的上下限。另外，需要强调的是，这里的活化能Q是指使岩石发生蠕变的活化能，该值与岩石类型和粒度大小有关[59]，比如Egea-Gonzlez 等人[38]在计算水星上名为柯伊伯地区(Kuiper region)的脆-韧转化带深度时，就选择了干的辉绿岩作为组成壳层的岩石类型，其粒度大小为10−3m，对应的活化能为4.85×105J·mol−1。

令式(7)等于式(8)，即可得到断层发育的最大深度，即脆-韧转化带的最大深度z的表达式。从式(8)不难发现，脆-韧转化带的深度受温度T(z)的影响。Nimmo 和Watters[53]给出了一个在放射性产热元素均匀分布前提下的地壳-地幔结构的温度方程：

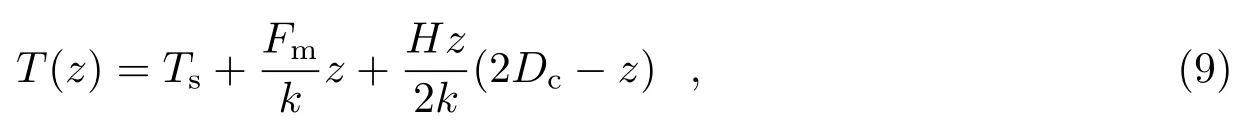
其中，Ts表示地表温度，Fm表示流入地壳底部的热流量，k表示热传导系数，H表示放射性元素产热率，Dc表示地壳厚度。

在选择了合适的参数后，Nimmo 和Watters[53]通过计算得出，水星表层脆-韧转化带的深度为30∼40 km，温度在800 K 左右。同样，Ritzer 等人[60]也通过计算得出，赤道地区2 条叶状悬崖下覆断层的深度为35 km。Egea-Gonzlez 等人[38]也通过计算得出，水星柯伊伯地区的脆-韧转化带深度为30∼39 km。他们重新定义了地壳-地幔结构的温度方程：

他们最终计算得出，水星柯伊伯地区脆-韧转化带温度为735∼819 K。通过计算脆-韧转化带的温度来研究水星壳层热结构，所得到的实际上是这些断层在形成时的环境温度。

另一种较为常见的方法是通过计算有效弹性厚度(effective elastic thickness)的方法来计算表面热流，从而构建壳层热结构。该方法已经被成功地应用在构建火星[61]、水星[62]、木卫三[63]等星球壳层的热结构。与脆-韧转化带不同，有效弹性厚度并非地层中真实的物理厚度，而只是反映岩石圈整体的脆性、韧性以及弹性强度的参数[64]。McNutt[65]最早提出通过等效强度包络法将有效弹性厚度与表面热流相联系的方法。因为韧性强度是与温度直接相关的，所以该方法的前提是实际应力对机械岩石圈(mechanical lithosphere)所产生的弯矩(bending moment)与有效弹性层弯矩相等，即：

其中，Melastic和Mmechanical分别为有效弹性层弯矩和岩石圈弯矩，K表示地形曲率，Teff和Tmech分别表示有效弹性厚度和机械岩石圈厚度，zn表示中性应力面深度，σ(z)表示在深度z处由于岩石圈弯曲而产生的脆性应力、韧性应力和纤维应力中的最小值。

脆性应力与韧性应力可分别由式(7)和式(8)计算得出。Turcotte 与Schubert[66]给出的纤维应力的定义为：

并且σ(z)需满足：

机械岩石圈厚度的基本定义为，岩石圈强度达到某一最低值时的深度，低于该深度时，强度不再有明显的变化[65]。对于类地行星而言，该最低值一般为10∼50 MPa[62,67]。对于有效弹性厚度的求解，现在较为常见的方法是对所获得的地形和重力数据进行分析[68,69]，如Audet[70]通过球面小波变换获得金星的有效弹性厚度，Gong 等人[71]通过地形与重力数据的相干性分析计算了月海玄武岩的厚度。一旦获得有效弹性厚度，就可以使用与式(9)和式(10)类似的温度方程求解表面热流，从而构建壳层热结构。Ruiz 等人[62]用此方法构建了水星北部平原地区的壳层热结构。

从式(9)和式(10)可以看出，要构建地壳-地幔结构的温度方程，需要对地壳-地幔中产热元素(heat producing elements, HPE)的丰度和分布进行详细的测定，尤其是分布在地幔中的HPE，其含量的高低将会直接影响从壳层底部流入的热流量。一般人们认为，水星的产热元素主要由K, Th 和U 等元素的放射性同位素组成[62,72−74]。从目前的情况来看，虽然信使号已经绘制出了水星表面包括放射性产热元素在内的主要化学元素的丰度，但是通过对信使号X 射线光谱仪和γ 射线光谱仪探测结果的交叉验证表明，水星表层只在几十厘米的深度范围内可以被认为是均质的[7,8]，即信使号所测量的仅仅是水星表层一定深度范围内的平均值。研究人员认为，内太阳系星球在太阳系早期曾经历过大规模的小天体轰击事件(被称为晚期重轰击[75])，水星表面星罗密布的撞击坑似乎也印证了这一点[76,77]。因此在实际研究中，大多数人认为，频繁而猛烈的撞击会使HPE 在水星地壳中得到充分的混合，即HPE 的分布在水星地壳中是均匀的。也就是说，用从水星表层测得的HPE 含量可以近似代表整个水星地壳中HPE 的平均含量[78,79]。HPE 作为亲石元素，在地幔分异过程中会随着分异的进行而逐渐在地壳中富集[74,78]，因此为了研究的方便，大多数研究者会直接假定HPE 在地幔中含量与地壳中含量的比值为定值ξ，典型的ξ值有0.2, 0.4, 0.5[62,72,74]。虽然对HPE 在地壳中均匀分布的假设，以及在壳幔中含量比值为定值的假设存在一定合理性，但是信使号γ 射线光谱仪的探测结果表明，水星北部大面积的火山平原和卡路里盆地(Caloris Basin)内部平原的主要化学组成与水星其他较老地区的差别明显，这表明它们可能是由化学演化程度更高的岩浆形成，并且与较老地区有着不同的地幔源[80]。这预示着随着今后更精细探测的进行，对于HPE 在地壳中的均匀分布以及在壳幔中含量比值为定值的假设需要修正，并且其结果将直接影响对水星壳层热结构的研究。另外，由于热能在水星壳层的运输以热传导为主，因此热传导系数k的取值至关重要。为了计算的方便，一般会假定地壳的热传导系数为定值[62,72,81]。但对地球地壳热传导系数的研究发现，热传导系数本身与物质的分子组成有关，且满足维德曼-弗兰兹-洛伦茨定理，受到温度的影响[82,83]。因此更真实的情况应当是，水星地壳的热传导系数是动态变化的，可能与深度有关。但由于问题的复杂性，在多数涉及到可变热传导系数的研究中，人们只是假设水星地壳热传导系数呈简单的线性变化[43,84]。在对月壳的研究中发现，由于大规模的撞击事件，月壳中形成了被称为月球浮土(lunar regolith)的层状结构[85,86]。因此，人们认为水星可能也存在类似的结构，并称之为巨风化壳(megaregolith)。Egea-Gonzlez 和Ruiz[72]研究了巨风化壳对于水星壳层热结构的影响，认为该结构像盖子一样覆盖在水星表面，从而增加了次表面的温度，降低了流出水星表面的热流。值得注意的是，在目前无法直接获得巨风化壳样本的情况下，将巨风化壳纳入这类热力学演化研究中时，考虑到水星与月球都经历过大规模的小天体撞击事件，一般直接认为水星的巨风化壳与月球浮土性质近似，在研究中所选用的参数也与研究月球浮土所选用的参数类似[16,72]。这样做的好处在于可以更好地关注这样的结构在热力学模型中所扮演的角色。但是由于水星的组成物质与月球的不同，它们的地质活动历史等也不同，因此，这样做会显著影响对水星巨风化壳的结构和孔隙度等的研究，进而影响对热传导系数等参数的测量。另外，考虑到巨风化壳是小天体撞击事件的产物，因此背后可能还涉及到更为复杂的动力学过程。综合来看，深入研究水星巨风化壳对于水星壳层热演化的影响也很有必要。

不管是通过研究脆-韧转化带的深度和温度来构建水星壳层热结构，还是通过有效弹性厚度来计算表面热流，都是操作性比较强的方式。但是作为一个热系统，水星本身存在高度复杂性，想要相对全面地构建水星壳层热结构，其难度巨大。壳层的热演化还受到来自深内部演化的影响，特别是水星还拥有与地球类似的偶极磁场[87,88]。尽管这为研究水星深内部的热演化提供了契机，但同时由于水星磁场强度过低[89]，因此，利用地磁发电机等理论来研究水星深内部热演化也面临巨大挑战[90,91]。通过对水星表面主要化学元素的研究发现，水星在形成早期，金属核与硅酸盐壳分异时处于高度还原的化学状态[7,8]。在这样的化学状态下，Si 元素会随着核-幔分异进入到液核中，并与Fe 形成Fe-Si 合金液核或Fe-Si-S 合金液核。随着演化的进行，它们可能会在液核顶部结晶，并形成FeS 固体层，而这个过程会显著影响因为内核冷凝所释放的重力势能和潜热能，进而影响进入地幔底部的能量[92]。除此之外，在地质时间尺度上，岩石星球的地幔表现出流体性质，因此对类地行星的研究还需十分关注是否存在地幔对流。现在的水星是否存在地幔对流的问题，或者说曾经的地幔对流等对于水星壳层热结构的影响等问题，都是不可忽略且值得深入探讨的[93−95]，也是今后研究的重点方向。因此，本研究团队将在Sori[96]以及Srivastava[97]对于水星表层物质组成和可变热传导率研究的基础上，探讨巨风化层对水星壳层热演化的影响。同时，我们也将在Hauck等人[92]以及Knibbe 和Van Westrenen[84]的研究基础上分析FeS 固体层在水星热演化中所扮演的角色。

5 水星地壳厚度

水星的地壳厚度是人们了解其演化历史的关键参数之一。通过研究水星的地壳厚度，人们能够了解水星内部结构、地质活动(史)以及热动力学演化的信息[78,96]。研究地壳厚度及其结构，是地球物理学科的重要课题，常用的方法包括地震波速法[98]、卫星重力测量反演[99]、重力/地形导纳法[100,101]等，其中又以地震波速法最为可靠。目前人们只在地球[98]和月球[102]获得过可靠的地震观测数据。但据悉，洞察号(InSight)火星探测器已于近期登陆火星。利用其携带的地震仪等科学设备[103]，人们有望获得火星的地震探测数据。目前，由于缺乏水星的地震数据，人们主要采用卫星轨道数据反演得到水星重力场，然后再反演[99,104]，或者用粘度松弛模型[53]或重力/地形导纳法[78,96]等方法研究水星地壳厚度。

对于类地行星(如地球)，用重力场反演其壳、幔密度和结构，需要进行地形补偿改正。通常人们先对其进行自由空气校正和布格校正，然后再采用普拉特或艾里均衡补偿模型对其进行改正。Anderson 等人[104]假设水星地壳适用艾里均衡补偿模型，并通过比较地基雷达测得的水星赤道扁率与水手10 号轨道数据得到的二阶球谐重力系数C22，得出水星地壳厚度为100∼300 km 的结论。Nimmo[13]建立了水星地形粘度松弛模型，即水平的地形变化会产生水平的压力梯度，并在一定温度下会导致下地壳发生流动而使得地形松弛。现有的证据表明，经过漫长的地质时期，长波段地形依旧存在，这说明长波段地形没有随着地形粘度松弛而消失。为了满足长波段地形在粘度松弛模型中的长期存在，Nimmo 将地壳厚度约束到100∼200 km 的范围。随后这一数值又被修订到小于140 km，以使其与在断层深度方面的研究结果一致[53]。信使号在进入水星轨道之前，对水星进行了三次飞越式探测[99,105]。Smith 等人[99]利用信使号对水星飞越式探测期间获得的有限精度(分辨率)的地形和重力数据，在水星表面地质构造模型的约束下，得出水星平均地壳厚度约为50 km 的结论。James等人[6]利用信使号入轨后获得的水星地形数据和重力场数据进行双重反演，绘制出了水星平均地壳厚度图，并得出水星地壳厚度的下限为38 km。使用卫星轨道数据反演主要是利用激光或多普勒技术跟踪卫星，从而获得相关的轨道数据，进而构建重力场模型，来达到反演地壳厚度的目的[6,99]。但是在缺少陆地数据以及测高数据的前提下，通过这种方法建立的模型只能反映重力场长波部分的信息，因此，该方法天生存在缺陷。而粘度松弛模型是基于下地壳发生流动的假设，因此需要知道地壳中的放射性元素生热率(见第4 章关于HPE 的论述)和下地壳主要物质组成等信息，尤其是主要物质组成的不同会导致流变性质的巨大差异。由于粘度松弛模型中引入了过多不确定量，因此，通过该模型只能得出地壳厚度的大致上限[13]。所以，本节将重点回顾使用重力/地形导纳法研究水星地壳厚度的进展。

Wieczorek 和Phillips[106]提出，可以使用重力/地形导纳(geoid-topography ratios,GTR)来估算岩石星球的地壳厚度。其所依据的理论认为，若重力与地形在空间频率域内线性相关，则可以使用重力与地形在空间频率域内的比值(即导纳)来计算包括地壳厚度在内的地球物理参数。该方法已经被成功地用于计算月球高地、火星南部高地和金星的地壳厚度，以及月海玄武岩厚度[71,100,101,106,107]。Wieczorek 和Phillips[106]将地形导纳定义为：

其中，Zl表示联系地形与大地水准面的导纳函数(与阶数l有关)；Wl表示与地形功率谱有关的权重函数，代表球面上指定点在给定l阶的地形对总地形的贡献程度，它被定义为：

其中，S(l)表示l阶地形功率谱。

Padovan 等人[78]利用重力/地形导纳方法建立的地形与大地水准面的线性关系来估算水星地壳厚度，即

其中，N表示大地水准面高；b表示常数，它可以对重力产生影响，但与地形无关。

水星的大地水准面可以通过分析信使号飞行轨道数据得到[99]，地形则由信使号所携带的水星激光高度计(mercury laser altimeter, MLA)绘制[5]。但是由于信使号轨道的原因(轨道偏心率高，近地点在北半球，远地点在南半球，且轨道高度高)[108]，只能获得高精度的北半球地形数据[5,6,109]，因此，目前用该方法只能估算水星北半球的地壳厚度。使用重力/地形导纳方法估算岩石星球的地壳厚度，需要考虑具体的地形补偿模式。因为重力场球函数中阶数与波长存在明显的对应关系，总体来说，低阶重力场对应着长波长地形，并且需要考虑地形补偿，因此，可以认为导纳函数是与地形补偿模式相关的。目前较为流行的地形补偿模式有艾里均衡补偿模型和普拉特均衡补偿模型[101,106]。Padovan 等人[78]假设水星地壳适合采用艾里均衡补偿模型，即假设球壳中艾里均衡补偿模型中的每个等宽度柱体的质量相等，定义出l阶导纳函数(简称等质量导纳函数)：

其中，ρc表示水星地壳密度，Rm表示水星平均半径，Rp表示水星平均密度。由式(17)可知，在已知地壳密度以及GTR值的前提下，可以反算出地壳厚度。在采用了地形以及大地水准面数据之后，Padovan 等人[78]认为，l范围取9∼15 是符合艾里均衡补偿模型的，因为在艾里均衡补偿模式下，GTR值应该趋于定值，并取GTR=9 m·km−1为最佳值。他们最终得出的水星地壳厚度为35±18 km。不难发现，影响用重力/地形导纳方法估算地壳厚度精度的最主要因素是地壳密度的数值。传统上，人们使用高分辨率的重力场数据来反演地壳密度，比如Wieczorek 等人[110]就采用了大于150 阶的重力数据计算了月壳的密度。但是采用信使号的轨道数据所获得的水星重力场数据的阶数偏低，因此，早在信使号还在对水星进行飞越式探测期间，Smith 等人[111]就已经对信使号进行轨道追踪，并发布了4 阶重力场数据。在信使号入轨之后，他们又将重力场数据扩展到20 阶[99]。Verma 和Margotv[112]以及Mazarico 等人[113]分别分析了信使号长达3 a 的雷达追踪数据，最终分别得到了40 阶和50 阶的重力场数据。Sori[96]认为，目前已发布的重力场数据的分辨率不足以较精确地反演水星地壳密度，因此，他提出通过计算颗粒密度(grain density)的方式间接计算体密度：

其中，ρg表示颗粒密度，ρb表示体密度，ψ表示孔隙度。

信使号携带的X 射线光谱仪和γ 射线-中子探测仪已经探测出水星表面主要化学元素的丰度[7,8]。出于对鲁棒性的考虑，Sori[96]认为水星表面各主要化学元素可以以氧化物形式存在(如SiO2, Al2O3, MnO, MgO)，也可以以硫化物的形式存在(如MgS, FeS)。他最终依据规范矿物学[114]分别计算出上述两种情况下，平均颗粒密度均为2 900∼3 000 kg·m−3[96]。Wieczorek 等人[110]认为，水星表面与月球高地存在相似性，因此，Sori[96]选择将水星表面的孔隙度定为0∼12%，并最终得到地壳密度为2 700∼3 100 kg·m−3。严格来讲，根据颗粒密度计算出的地壳密度也是有明显缺陷的，因为这种方法也是建立在地壳充分混合的假设之上，并且孔隙度的选择也给最终结果带来较大误差。但是在当前情况下，这似乎是一种退而求其次的方法。

Hemingway 和Matsuyama[115]发现，在艾里均衡补偿模型中，每个等宽度柱体的质量相等的假设，会导致导纳函数偏小，从而使得计算出的地壳厚度偏大，因此他们重新定义了每个柱体在等深度处等压力情况下的导纳函数(简称等压导纳函数)：

其中，Mm表示水星总质量。

Sori[96]采纳等压导纳函数，同时，为了与Padovan 的结果相比较，同样选择GTR=9 m·km−1为最佳取值，重新计算了水星地壳的厚度，其结果为(26±11) km。James 等人[6]发现水星的长波段地形确实是被补偿的，所以有理由认为(26±11) km 的地壳厚度是可信的。不管是Padovan 等人[78]的研究结果，还是Sori[96]的研究结果，都将水星地壳厚度大幅修订到了30 km 左右。但是总体来看，由于没有获得高分辨率的重力场数据，因此，以上方法还是存在明显缺陷的。贝皮·科伦布号作为一种复合式的探测器，有望像Grace 重力卫星[116]那样，通过测量探测器之间的相对距离和速率变化来得到高分辨率的重力场数据，这很可能会带来一些突破性的成果。

对水星天平动的研究证实，水星地壳-地幔厚度应该在400 km 左右[117,118]，因此地壳厚度占整个硅酸盐壳层厚度的比值约为7%。这一结果使得水星拥有太阳系类地行星中最高的地壳产生率，且与月壳产生率接近[110]。这是否预示着水星的地壳产生过程与月壳的类似？另外，如此薄的地壳厚度，又是否可能是由于水星早期经历过剧烈的撞击，导致大量地幔物质被剥蚀而最后形成的呢[78,113,119]？一系列的问题有待被解决。