基于TerraSAR-X 卫星数据的内孤立波参数和海表流速信息提取的探索研究

2020-01-18曾智李晓明任永政陈学恩

海洋学报 2020年1期

曾智，李晓明，任永政，陈学恩*

( 1. 中国海洋大学海洋与大气学院，山东青岛 266100；2. 海南省地球观测重点实验室，海南三亚 572029；3. 中国科学院空天信息研究院数字地球重点实验室，北京 100094)

1 引言

海洋内波是发生在稳定层化的海洋内部的一种波动。南海北部是全球内波最为活跃的海域之一，也是内波研究的热点区域[1-3]。利用合成孔径雷达（Synthetic Aperture Radar，SAR）可以反演内波的多种动力学要素，比如内波传播方向[4-7]、内波传播相速度[6-8]、混合层深度[7,9]、内波振幅[6,8,10-14]等。而其中内孤立波振幅的反演是最具挑战性的研究内容。最早利用SAR 图像开展内孤立波振幅反演工作的是Apel 和Gonzales[10]。他们提出反演振幅的波长变化法，即通过SAR 图像测量出一个波包内逐个波的波长，然后用模式函数来确定每个波的振幅。但该方法仅适用于较规则且波长渐进变小的波动。Zheng 等[6]推导出利用内孤立波SAR 图像计算内孤立波半波宽度的曲线拟合法，并基于KdV 方程[15]建立了一种两层海洋的模型用以内孤立波SAR 遥感仿真研究。之后诸多学者对此模型进行了优化，例如甘锡林等[8]通过希尔伯特-黄变换法代替曲线拟合法来确定内孤立波波长，并认为该方法更适用于波列形式的内孤立波；Xue等[13]针对大振幅内孤立波，提出利用更高阶数值方程反演振幅的方法。然而，两层海洋模型在刻画实际海洋时具有较大的局限性，因为KdV 方程仅适用于浅海内波[15]，而在反演深海大振幅内孤立波有关参数时会造成较大的误差[13]。与两层模型法不同，王晶等[14]建立了一种三层海洋的分层模式并求得该模式下的非线性薛定谔方程，然后借助傅里叶方法反演内孤立波有关参数，其振幅结果符合甘锡林等[12]对南海内孤立波振幅的统计结果。三层海洋模式相较于两层模型更接近于真实的海洋，但其计算复杂程度远大于两层模型，并且事实上也未能完全模拟出真实的海洋状况。考虑到真实海洋中海水的连续层化，曾侃[11]提出了一个参数化振幅反演方法并应用于ERS-2 获取的东沙岛以北海域内孤立波SAR 图像，其反演得到的振幅为4.8 m，而通过两层模型法得到的振幅结果仅为1.3 m。对比亚洲海国际声学实验的CTD 数据，参数化法结果更接近于现场的观测值（振幅≥5 m）。

对于海表流场的反演，近年来随着空间科学技术的发展，利用卫星高度计数据计算流场已经成为海表流场估算的有效方法[16]。卫星高度计资料虽然可以全球覆盖，但空间分辨率低，仅适用于研究大范围的海洋变化[17]，比如地转流、海表面高度等。在近岸海域，高度计在发射和接受信号时会受到陆地污染、大气误差等方面的影响，使得沿岸至少50 km 范围内海表流场的观测结果存在较大误差[18]。相比于高度计卫星，SAR 卫星具有全天时、全天候、高分辨率和宽刈幅成像的优势[19]，使其成为一种更有效的测量海表流场的技术手段。Goldstein 等[20-21]首次提出利用顺轨干涉（Along-track Interferometry，ATI）技术测量海表流场，并利用机载SAR 获取的2 幅图像间的相位差成功估计了美国加利福尼亚使命湾、旧金山湾和圣地亚哥湾的海表流场。之后，Romeiser 和Thompson[22]对海表流场的ATI-SAR 成像机制进行了数值模拟研究，证明了机载和星载ATI 技术测量海表流场的可行性。目前国内外对于ATI-SAR 数据的处理大多基于M4S 模型[22-28]。M4S 模型软件是一个较为成熟的模拟流场调制下合成孔径雷达后向散射系数以及成像的软件。利用M4S 模型软件可以对海浪运动的影响进行校正[22]，从而反演得到海表流场。例如，任永政[24]利用SRTM（Shuttle Radar Topography Mission）数据反演丹麦小贝尔特海峡的海表流场，其流速结果与声学多普勒流速剖面仪（Acoustic Doppler Current Profilers，ADCP）实测数据相差0.16 m/s 左右，反演误差在20%以内；范开国等[25]以南海海区3 景海洋内波SAR 图像为例，借助Alpers-Hening[29]理论、二分法等方法进行内波SAR 的仿真研究。结果显示仿真的海面后向散射强度剖面与SAR 实际观测较为吻合，相关系数达90%以上。2007 年，德国发射TerraSAR-X（TSX）卫星，提供了迄今为止唯一的星载顺轨干涉SAR 数据。Romeiser 等[26-27]通过TSX 在双接收天线（Dual Receiver Antenna，DRA）模式下获取的顺轨干涉数据[30]反演德国易北河河口、苏格兰北部海域等地的海洋表层流场。易北河河口流速反演结果与Un-TRIM 模式结果相比误差在-0.11～0.08 m/s 之间，整体相关系数为0.88。此外，他们还对流速反演的影响因子进行了探讨。最近，Romeiser 和Graber[28]基于M4S 模型设计了反演内孤立波参数的仿真模型并应用于TSX 获取的南海东沙岛附近的ATI-SAR 图像，结果显示内孤立波导致的海面后向散射强度剖面与实际SAR 图像上的信号剖面基本吻合。对于ATI-SAR数据的处理，除了利用M4S 模型，还可以从理论上直接去除多普勒速度[31]组成项中的非海表流速项（本文称之为直接分离法），余项即为海表流速项。非海表流速项主要包括净布拉格波相速度[31]和大尺度波轨道速度[31]。Shemer 等[32]在Monterey Bay 的ATI-SAR飞行试验中考虑了沿不同方向传播的布拉格波的贡献，但是其场景设置不具有普遍性。Graber 等[33]提出了根据先验风场和波浪信息并结合微波散射模型的方法计算净布拉格波。其反演的流场结果与岸基HF 雷达测量结果一致。之后，Kim 等[34]提出了利用L，C 双波段ATI-SAR 数据进行净布拉格波相速度消除的方法。该方法最大的优势是不需要风向信息，但是迄今为止能同时接收L 和C 两个波段数据的ATISAR 平台较少。对于大尺度波轨道速度的消除，目前通常是利用轨道速度沿海浪传播方向具有周期性的特点[31]，通过空间平均的方法来处理。

基于上述研究现状，本文的研究重点可归纳为：基于TSX 的ATI-SAR 数据，利用其后向散射强度信息反演内孤立波的振幅和相速度，对比不同方法得到的结果；利用其干涉数据反演海表流场，也对比不同方法得到的结果；最后通过内孤立波对海表流动的调制作用计算波致表面流对反演得到的实际流场的贡献。

2 数据介绍

TSX 卫星是德国2007 年6 月15 日发射的工作于X 波段（9.8 GHz）的星载SAR 卫星[35]，以近极地轨道飞行。其天线长4.8 m，入射角20°～40°。TSX 可以通过DRA 模式，即它的天线可以分成两个独立部分来接收信号[36]，从而获得短基线长度的顺轨干涉数据。图1 为TSX 工作于DRA 模式下的示意图。工作于该模式时，顺轨干涉基线长度为1.15 m。主部分Fore 向目标物发射信号，之后主部分Fore 和次部分Aft 均接收来自目标物的后向散射信号。由于顺轨基线的存在，两部分天线接收到的信号会存在时间差。通过该时间差可推算出目标物沿雷达视向上的移动速度。相对于搭载两个独立的信号发射器，DRA 模式既节省了成本，又提高了数据处理效率。

本文采用的两幅SAR 图像为TSX 卫星于2010年4 月22 日22:13 UTC 在东沙岛（20.55°N，116.87°E）及其附近海域获取的条带模式（Stripmap）的DRA 数据。数据存放形式为单视斜距复数据（Single Look Slant Range Complex Data，SSC），相关信息如表1所示。

SSC 级别的数据产品由复数表示，在斜距向和方位向上有相等的像素尺寸，同时具有幅度和相位信息。对于天线上两个不同接收部分对同一场景获取的两幅图像，设图像1 上的任一点对应于图像2 上的，有

图 1 TSX 卫星的DRA 工作模式示意图Fig. 1 Demonstration of DRA mode of TerraSAR-X satellite

表 1 TSX 获取的SAR 图像的基本信息Table 1 Technical specification of the TerraSAR-X ATI data

图 2 TSX 卫星在东沙岛附近获取的快视图（2010 年4 月22 日22:13 UTC）（a），对应该快视图的雷达后向散射强度（b），降噪处理后对应快视图的相位差（c）Fig. 2 Quicklook of the TSX scene acquired over Dongsha Island at 22:13 UTC on April 22, 2010 (a); the corresponding radar backscatter intensity of the TSX scene (b); the derived phase difference from the ATI data of the TSX scene (c)

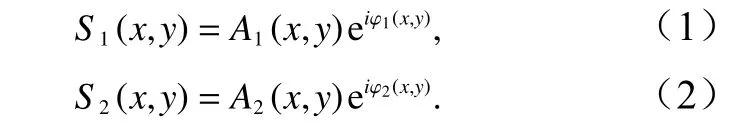
φi(i=1,2)

式中，Ai和分别表示振幅和相位。将它们共轭相乘即得到复数据

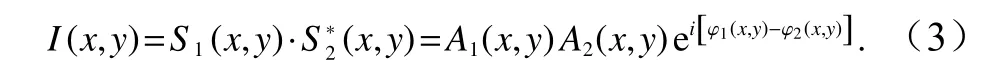
其中后向散射强度为

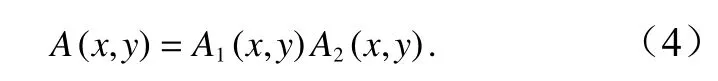
干涉相位差为

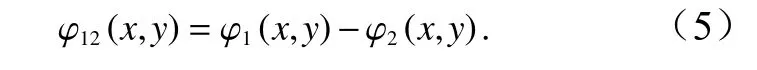
图2a 所示为本研究中使用的TSX 获取的快视图。图2b 为利用公式（4）并经过辐射校正得到的后向散射强度分布，用于之后内孤立波参数的提取研究。图2c 为利用公式（5）并进行降噪处理得到的干涉相位差分布，用于之后海表流场的反演研究。

SAR 图像（图2a）中内孤立波向西北向传播，亮暗条纹分布状况为亮条纹在前，因此内孤立波类型为下降型内波[37]。内孤立波分布在东沙岛的南北两侧，这是因为内孤立波西传时遇到东沙岛发生了绕射现象[2]。Jia 等[38]基于ENVISAT/ASAR 图像对东沙岛绕岛的内孤立波进行了统计并设计了数值模型探究绕岛后内孤立波的变化特征。本文TSX 图像中的内孤立波，其北支波峰线的长度在图中就超过了70 km。南支内波条纹的明暗程度大于北支，说明其振幅大于北支[37]。这是因为东沙岛南侧水深大于北侧，因此北支内波能量耗散程度更大[39]。以下将详细阐述利用该景TSX 后向散射强度数据定量反演内波的振幅和相速度，再利用干涉数据反演海表流场的研究工作。

3 内孤立波参数的提取

3.1 利用经验模态分解法提取特征半宽度

图2b 中5 处断面，分别平均成沿波动传播方向的一维数据，然后使用经验模态分解法处理得到若干层不同频率的信号。每一层称为一个本征模态，其中必有一个模态包含内孤立波的主要信息[40]。将分解得到的每一个模态求方差并归一化，

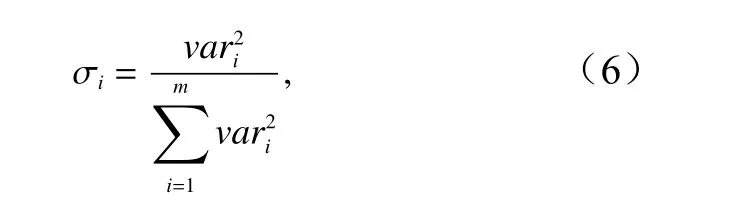
式中，m代表分解的模态个数；vari代表第i个模态的方差。归一化方差σi体现了每个模态相对能量的大小。甘锡林等[8]认为，由于内孤立波的能量非常大，故归一化方差σi最大的那个模态代表内波信号并且其曲线形状应与后向散射强度的形状相似。

以断面1 为例，其平均雷达后向散射强度分布及分解得到的8 个模态如图3 所示。计算这8 个模态的归一化方差，结果如表2 所示。第4 个模态的归一化方差最大，且其曲线形状与后向散射强度曲线相似，因此可认为第4 个模态代表内孤立波信号。

进而通过该模态中极大、极小值对应的x轴坐标的间距计算明暗条纹间距的平均值D。之后利用经验公式[41]计算内孤立波的特征半宽度l，

按照上述处理流程，分别得到其他5 个断面内孤立波特征半宽度，如表3 所示。

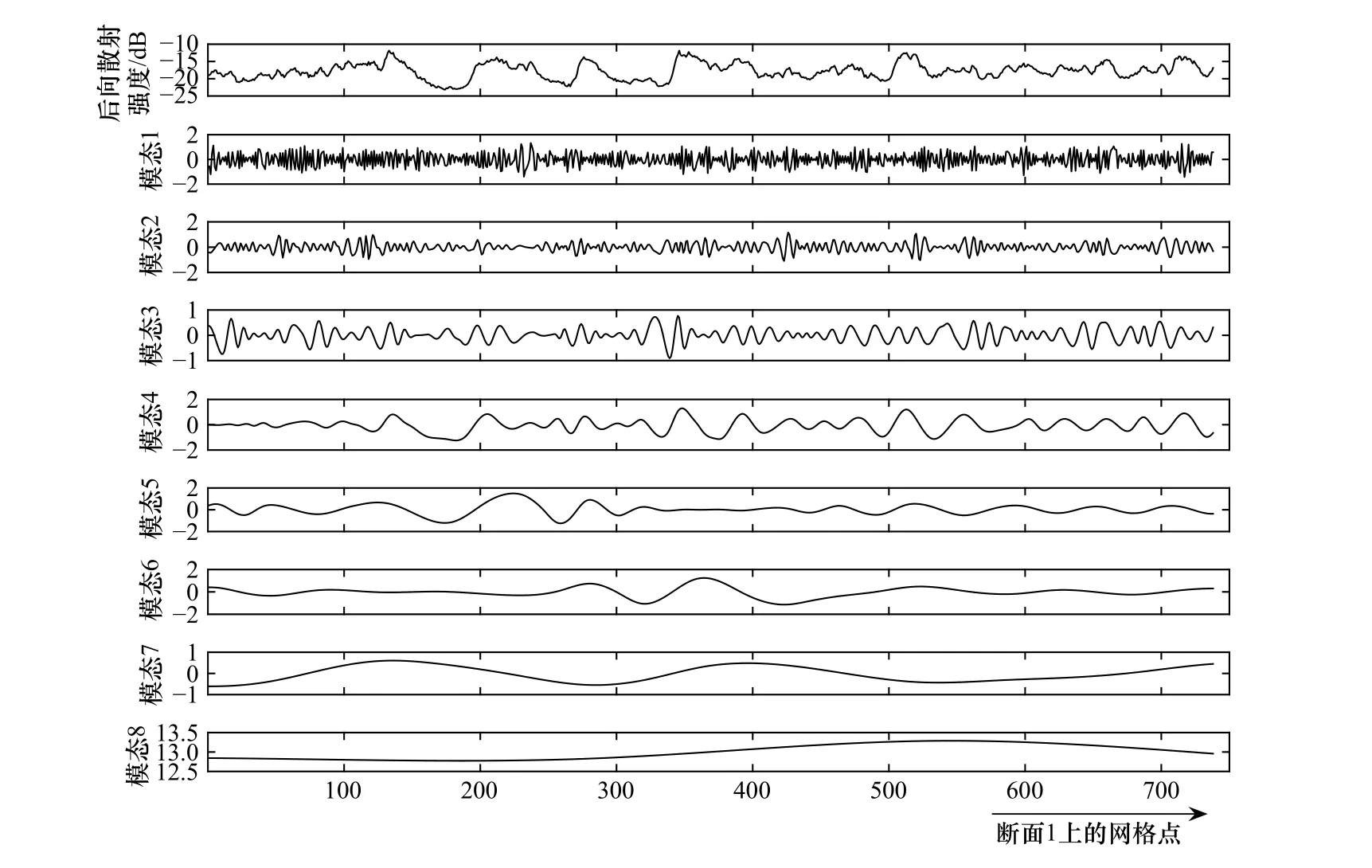
图 3 沿内孤立波传播方向的断面1 平均后的后向散射强度数据（a）；b-i 为经验模态分解法得到的8 个本征模态Fig. 3 Distribution of the averaged backscatter intensity of Transect 1 along the propagation direction of the internal wave (a); b-i are 8 intrinsic modes

表 2 不同模态的归一化方差Table 2 Normalized variance of the 8 intrinsic modes

表 3 图2b 中各断面内孤立波特征半宽度Table 3 Characteristic half width of internal solitary wave in each transect in Fig.2b

3.2 振幅与相速度的反演

通过TSX 后向散射强度数据获取了内孤立波的二维信息—特征半宽度。以下，分别利用两层模型法和参数化法进一步反演内孤立波振幅和相速度参数。

3.2.1 利用两层模型法反演振幅与相速度

在一个由上下两层不同密度海水组成的海洋系统中，设上层深度为h1，下层深度为h2，则非线性自由长波在水平方向x上传播的KdV 方程可简化[42]为

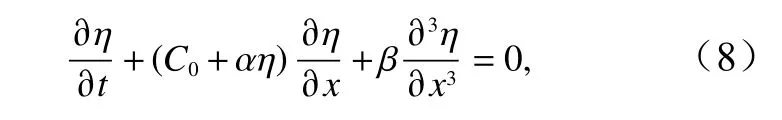
式中，η为内孤立波的垂向位移；参数C0、α、β分别为线性波速、一阶非线性项系数、弥散项系数。在垂向z上内波的垂向模态方程[9]为

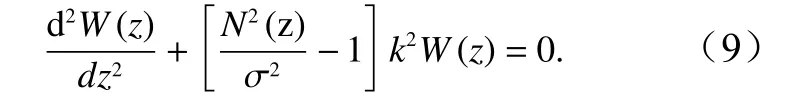
式中，其中W(z)表示内波的本征函数；N2(z)为浮性频率；σ为内波角频率；k为水平波数。根据式（8）和式（9）可分别得到内波振幅（η0）表达式和频散关系式为

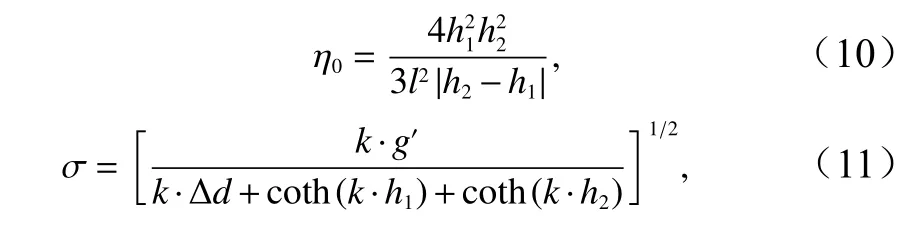
式中，l为内波的特征半宽度为约化重力加速度，其中为重力加速度，为两层海水之间的密度差，ρ为海水平均密度。

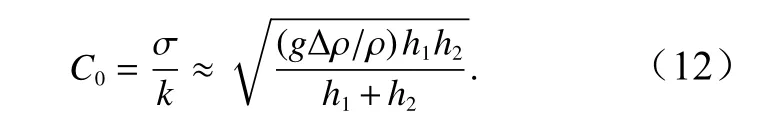
内波的相速度为

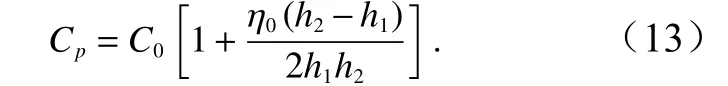
在相速度表达式（13）中，方括号中第二项远小于1，在该海域中的内波相速度约等于线性波速。

基于GBECO_2014 地形数据得到研究海域内的水深分布如图4a，再利用WOA2013 温盐数据计算5 个断面的浮性频率剖面。由于5 个断面相距较近，WOA2013 数据不足以精确匹配各个断面，因此断面1 单独使用一组温盐数据，断面2 和3 使用相同的温盐数据，断面4 和5 使用相同的温盐数据。

以断面1 为例，计算得到的浮性频率剖面如图4b所示。在水深72.50 m 处有最大值，可认为是跃层深度h1。断面1 水深h=525.00 m，故h2=452.50 m。利用加权平均法可得上下两层海水密度分别为1 022.88 kg/m3和1 025.01 kg/m3。代入式（10）、式（12）和式（13）可得内孤立波的振幅为6.72 m，相速度为1.07 m/s。按照上述流程操作可得其他4 个断面内孤立波振幅与相速度，如表4 所示。

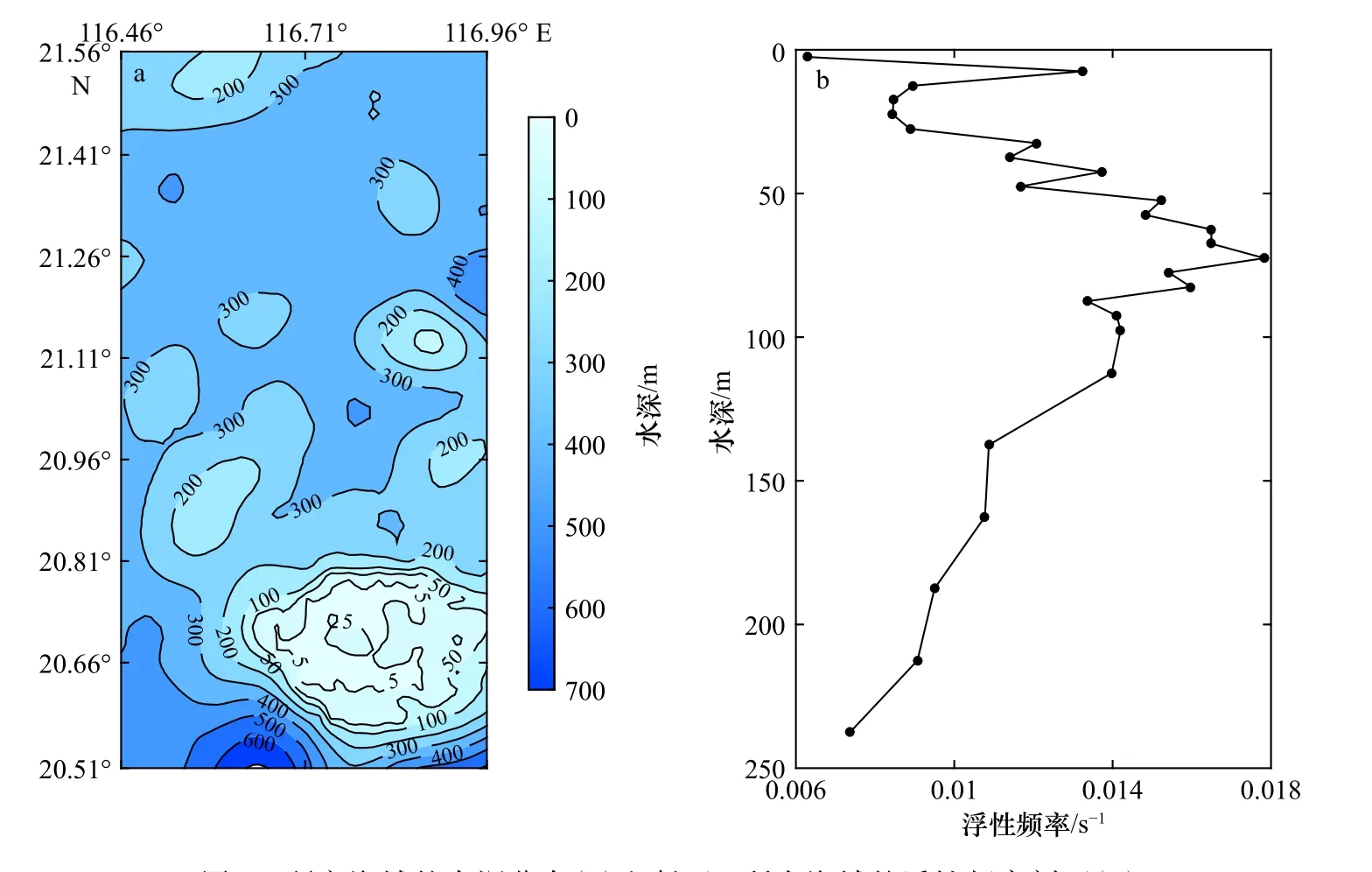
图 4 研究海域的水深分布（a）和断面1 所在海域的浮性频率剖面（b）Fig. 4 Bathymetry of the research area (a) and profile of buoyancy frequency of Transect 1 (b)

表 4 利用两层模型法和参数化方法提取得到的图2b 中5 个断面内孤立波的振幅和相速度Table 4 Amplitude and phase speed of internal solitary waves in the 5 transects marked in Fig. 2b, obtained using the two-layer-model and the parameterization method

3.2.2 参数化法提取振幅

两层模型法是把跃层看作分界面，由上下两层密度均匀的海水组成。但在实际海洋中，海水密度的垂向变化是连续的。基于此，曾侃[11]提出了参数化法，刻画了海水密度的连续分层特征。该方法使用一个三参数的曲线族来模拟垂向z上海水的浮性频率，

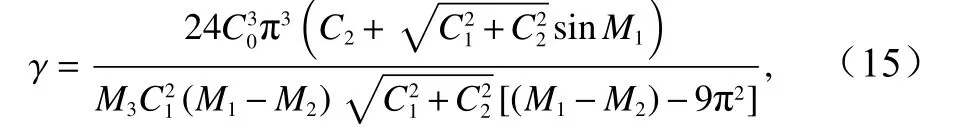
之后内波的振幅η0可由下式求得，

利用该方法反演得到的5 个断面的内波振幅如表4 所示。由于参数化法只给出了水深、波长与振幅相关的参数，因此无法提取内波的相速度信息。

3.2.3 结果对比与分析

Ramp 等[43]在东沙岛附近进行了1 个月左右的锚链观测，观测时间为2001 年4 月21 日至5 月19 日，对到达S7 站位（21.61°N，117.28°E，水深350 m）的内孤立波的振幅和相速度进行了统计，结果显示振幅约为35～70 m，相速度约为1.16 m/s。

针对振幅反演，两层模型法得到的结果与历史实测数据相比差距非常大。因此，针对该例，两层模型法得到的振幅结果是不恰当的。相比于两层模型法，参数化法得到的结果就更加合理一些。其可能的原因包括3 点：一是东沙岛附近属于浅水海域，由于参数化法相当于减小了恢复力[11]，因此其反演浅水内孤立波振幅时情况会更加理想；二是内孤立波振幅与波长的关系对层化条件的依赖性很强。当跃层的相对厚度很大的时，两层模型不再适用[44]；三是两层模型对于水深和跃层深度数据的准确度要求很高，由于WOA 2013 数据与本文选取的内孤立波区域的地理位置不能精确匹配，故存在一定的误差。

然而参数化法得到的结果与实测值相比也偏小。一方面，参数化法在反演过程中采用了一些假设和近似，如跃层厚度的定义[11]和计算等，因此反演得到的结果会存在一定的误差。另一方面，本文选取的5 个断面均在S7 站位的西南方约0.7°左右。东沙岛附近的海底地形，其局地水深深度变化剧烈。内孤立波在这种地形上西传过程中会与底地形摩擦发生能量耗散，其振幅和相速度均会减小[39]，因此理论上在5 个断面上整体的内孤立波振幅会小于内孤立波传至S7 站位时的振幅。针对本例，利用参数化方法得到的内孤立波振幅约在21～39 m，在误差允许的范围内，可认为振幅反演结果与历史同期数据基本符合。

对于相速度反演，利用两层模型法得到的相速度的平均值约为1.09 m/s，与实测值相差较小，反演结果合理。因此，我们认为在东沙岛浅水海域，参数化法较两层模型法能更好地反演内孤立波振幅，但两层模型法能很好地反演内孤立波相速度。

4 海表流速信息提取

4.1 ATI-SAR 海表流场提取基本原理

由于多普勒频移效果[31]的存在，沿卫星轨道方向配置的两个天线接收的两幅SAR 复图像的相位差正比于SAR 后向散射信号的多普勒频移。两个顺轨SAR 天线以相同几何方式获取同一海面的两幅SAR图像，当两幅图像获取时间间隔足够短，这两幅SAR图像可以产生干涉，从干涉相位可提取沿雷达视线方向的海表流场分量（图5）。由于两天线间基线距离导致到同一运动目标存在路程差，导致回波信号到达两个天线存在时间差Δt，则两幅SAR 图像的相位分别为

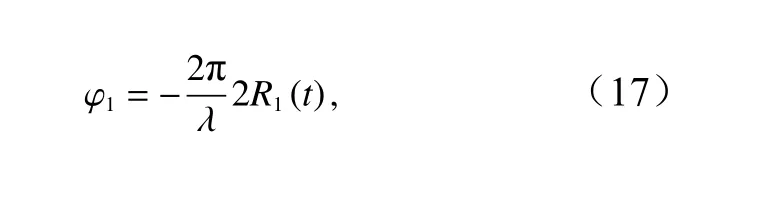
图 5 顺轨干涉SAR 海表运动速度提取示意图Fig. 5 Diagram of derivation of sea surface velocity using ATI-SAR

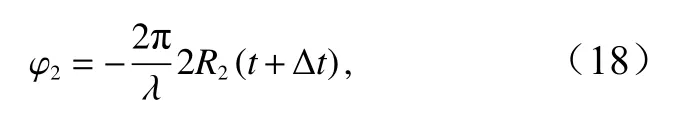
式中，λ为雷达波长；t为天线测量时刻；Δt为滞后时间分别为两天线到目标的斜视距离。相位差可表示为

其中多普勒速度Vr为目标在雷达视线方向上的分量。上式变换后多普勒速度可由相位差表示

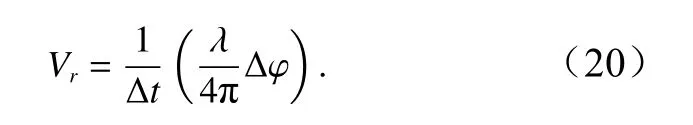
4.2 多普勒速度的计算

图2c 为基于公式（19）得到的相位差分布。负值表示海表远离雷达运动。由于TSX 图像已进行过图像配准，因此可直接利用相位差数据计算沿雷达视向的多普勒速度。根据公式（20），其中可用表示，平台移动速度Vs=7 098.23 m/s，干涉基线长度b=1.15 m，得到的多普勒速度分布及其统计直方图如图6所示。

由图6 可以看到，内孤立波波峰线附近的多普勒速度值较大。全场的多普勒速度主要分布在-0.50～-2.20 m/s 之间，平均值为-1.39 m/s，在-1.40 m/s 附近分布较集中。由于这是TSX 获取的一幅降轨数据，雷达视向为右视，海表运动速度整体为负值，表明该时刻海表运动速度存在一个远离雷达视线方向的运动分量。而此例中内孤立波传播方向为西北方向，通过正交分解，可以得到一个远离雷达视线方向的运动分量，因此，图6a 反映的海表运动速度场，与实际海洋状态吻合。

4.3 利用M4S 模型计算海表流速

图 6 利用TSX 的ATI 数据得到的多普勒速度的空间分布（a）和对应的多普勒速度值统计直方图（b）Fig. 6 Spatial distribution of the derived Doppler velocity from the TSX ATI data (a) and statistic histogram of the corresponding Doppler velocity (b)

M4S 模型[22]是针对海表流场和风场微波成像的数值模拟软件，包含两个主要模块。一个模块是浪-风-流模块，用于计算给定的海表流场和风场下的海浪波谱的变化；另一个模块是雷达模块，用于将海浪谱转化为标准化的后向散射截面、干涉相位等信息。

利用M4S 模型软件可以对多普勒速度场进行校正[22]，以反演出实际的海表流场。校正时，输入的数据文件包括3 个部分。一是网格化的多普勒速度场和风场；二是卫星雷达的参数如轨道高度、移动速度等；三是水深等调节参数（该部分为缺省设置）。网格化的多普勒速度场一般设置为正方形网格，以加快计算速度。在校正的过程中，M4S 模型考虑了多种海浪谱、风场校正和作用量方程的多源函数等因素。校正结束后，输出的内容包括一个新的海表流场。将此流场与初始输入流场比对，若相差较大，则根据这两个流场设计一个新的流场并再次作为输入，继续利用M4S 模型进行校正。经过反复迭代运算，若输出与输入流场差值小于所设阈值，则反演结束。

将4.2 节得到的多普勒速度进行降噪处理后作为第一猜测流场输入M4S 模型。由于没有对应时刻的风场数据，因此采用最近时刻的数据，为ASCAT 卫星于2010 年4 月23 日01:26 UTC 获取的该海域的风场数据。输入的风场设置成全场均一，风速大小为10.63 m/s，风向为南偏西57.96°（去向）。卫星参数如轨道高度、基线长度、极化方式、入射角等均按照TSX参数设置。每进行一次计算，将输出流场与输入流场比较，阈值设置为0.01 m/s。迭代计算后，最终得到的海表流场如图7a 所示。

全场流速平均值大小由初始的1.39 m/s 降低为1.10 m/s，降幅为20.81%。在内孤立波的波峰波谷线区，流速值改变较大。由于内孤立波对表面短波的调制作用大于表面长波对表面短波的调制，因此在SAR图像会形成明暗程度较大的条纹[37]。M4S 模型的物理基础之一是波数谱平衡方程，故在M4S 模型处理数据过程中会对这种调制作用进行严密的校正。内孤立波区域本身的多普勒速度较大，M4S 模型对其运动进行的校正也较大，所以才导致这种波峰波谷区流速值改变较大的现象。

4.4 直接分离法计算海表流速

除了利用M4S 模型软件对多普勒速度进行处理之外，还可以从多普勒速度的组成成分上分析，进而从理论上提取出海表实际流速。海面多普勒速度主要由实际流速us、大尺度波轨道速度uo、净布拉格波相速度ub等组成[31]，

式中，uc为表面流场，包括潮汐流、洋流等；uwd为海表风引起的漂流。实际流速us为前两项之和，即us=uc+uwd。直接分离法就是将非实际流场项从多普勒速度中线性地去除，即除去净布拉格波相速度和大尺度波轨道速度。

4.4.1 净布拉格波相速度的去除

通常情况下，存在两个传播方向相反的布拉格波，一个与雷达视向相同，另一个则相反[34]。每一个布拉格波相速度值可以表示为

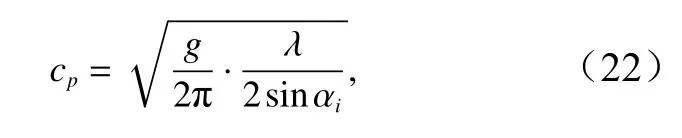
式中，g为重力加速度；λ为雷达波波长；αi为不同点的入射角。净布拉格波相速度为它们的加权矢量和，

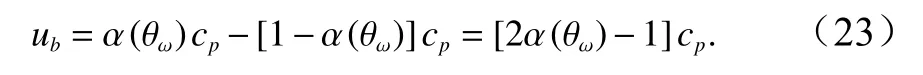
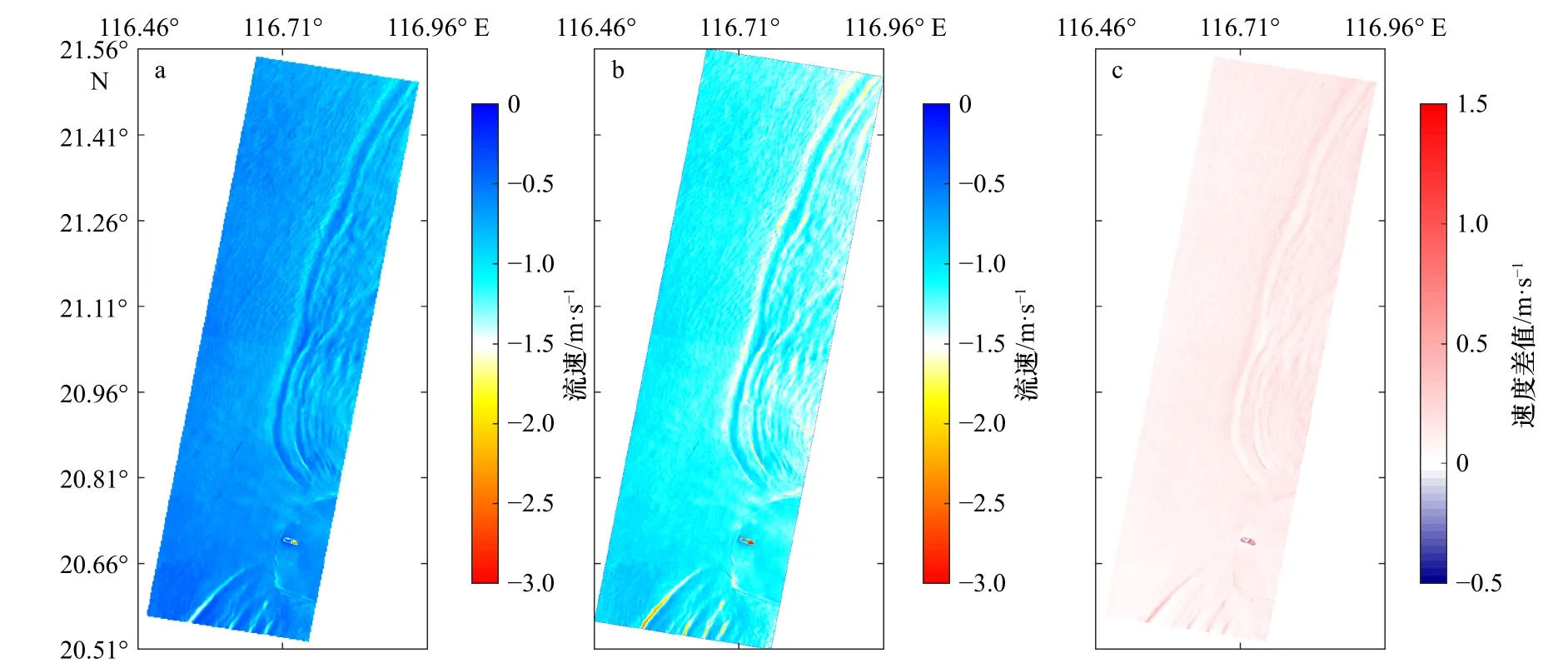
图 7 M4S 模型法得到的海表流速结果（雷达视向）（a），直接分离法得到的海表流速结果（雷达视向）（b），两者的差值（c）Fig. 7 Sea surface current speed (component in the line of sight) retrieved using the M4S model (a), sea surface current speed (component in the line of sight) derived using the separation method (b); differences between the two retrievals (c)

顺风情况下，θω=0°，α=1；逆风情况下，θω=180°，α=0。而在侧风情况下，权重因子与风向的关系目前还没有一个精确的理论模型。参照Graber 等[33]在计算波浪运动的贡献的过程中对于先验风场的处理，由于本文研究海域内的风向和流向的夹角小于90°，故近似为顺风情况，选取权重因子α=1。

根据式（22）和式（23）可得全场净布拉格波相速度的值ub分布于0.30～0.32 m/s 之间。将各点的多普勒速度减去对应的净布拉格波相速度，得到的速度场进而进行大尺度波轨道速度的去除。

4.4.2 大尺度波轨道速度的去除

利用轨道速度沿海浪传播方向具有周期性的特点，可通过空间平均的方法对其进行消除[30]。对TSX获取的快视图（图2a）进行图像谱分析，得到图像内的海浪波长约为百米级尺度。因此，采用500 m×500 m的窗口对4.4.1 节得到的速度场进行空间平均，得到的海表流速如图7b 所示。

4.5 结果对比

表5 列出了上述两种方法得到的结果与原多普勒速度的相关统计量。可以看到，两种方法得到的速度最大值、最小值、平均值均较原多普勒速度小。两者平均值大小很接近，均在1.10 m/s 左右。M4S 模型法对最大值的改变较大而直接分离法对最小值的改变较大。将M4S 模型法结果与直接分离法结果直接作差，差值图如图7c 所示。M4S 模型法得到的流速绝对值普遍略小于直接分离法得到的流速绝对值。两者差值较大的地方为内孤立波波峰波谷线区域。由于直接分离法是对整个流场进行统一处理的，所以这种局部较大的差值说明了M4S 模型法在处理流速的过程中对于内孤立波区域多普勒速度的调整较大，进一步说明了其对内孤立波调制海表流动的过程有着较大的校正。那么，波致表面流在海表流动中能占多大的比例？下一小节将予以介绍和计算。

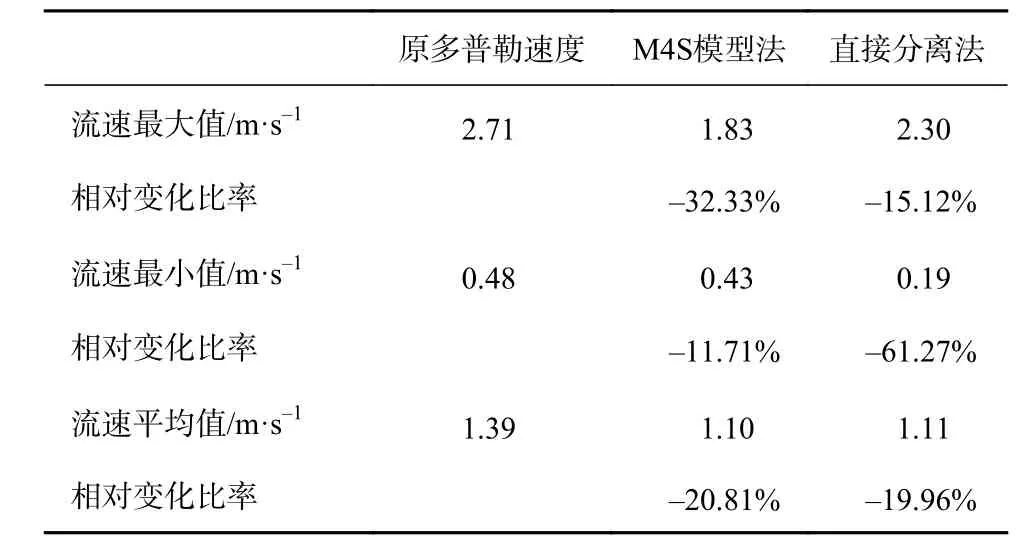
表 5 利用M4S 模型法和直接分离法得到的速度及原多普勒速度对比Table 5 Comparison of the velocities obtained by the M4S model method and direct-separation method and the Doppler velocity

4.6 波致表面流对于海表流速的贡献

利用上述两种方法得到断面1 内平均流速值大小均在1.10 m/s 左右，这是在雷达视向方向上的速度。接下来计算波致表面流动在该方向上对于总流动的贡献。

对于式（8）描述的KdV 方程，在内波传播方向x上，当弥散项和非线性项达到平衡时具有稳定态孤立波解[42]，

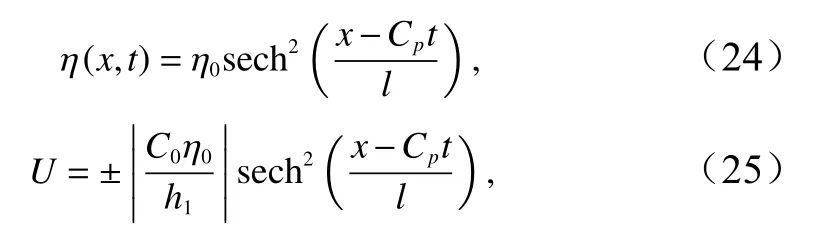
式中，η0为内波的振幅；C0和Cp分别为内波的线性波速和相速度；l为内波的特征半宽度；h1为上层海水的厚度；U为内孤立波传播引起的表面流在内波传播方向上的流速。对于下降型内波，式（25）取正号，上升型内波则相反。本文研究的内孤立波为下降型内波。在小振幅假定下，式（25）可近似为：

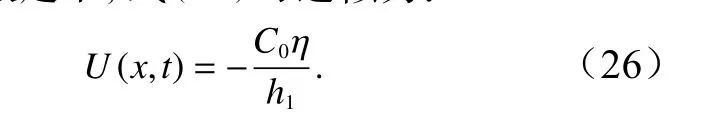
根据3.2 节的结果，将断面1 参数化法得到的振幅（38.69 m）和两层模型法得到的相速度（1.07 m/s）代入式（26）中，得到波致表面流U≈0.57 m/s。

将波致表面流投影到雷达视向方向上（雷达入射角29.54°，雷达的水平视向为北偏西79.46°），约为0.28 m/s，其与通过卫星反演得到的流速比值为0.23。这个比值可能存在一定的误差，其主要来源，一是在内孤立波参数反演过程中即使采用参数化法也不能完全模拟海洋实际情况，反演出的振幅与实际振幅有差别，而通过两层模型法得到的相速度也存在一定的误差；二是不管是M4S 模型法还是直接分离法，在反演海表流场的过程中采用了多种近似或者假设，这些都会带来一定的误差。