太阳能电池片无人自动化生产车间物流调度方法研究
2020-01-18李顺江何玉东
李 凡,李顺江,何玉东
(成都四威高科技产业园有限公司,四川 成都 610000)
1 引言
光伏业是未来最清洁、安全和可靠的能源,行业发展前景良好,智能物流可有效降低电池片在运送过程中的损耗并大幅减少现场用工需求,有效降低企业生产环节的成本,因此很多光伏企业在构建符合自身特点的智能工厂时,都将物流作为主要改造方向。智能物流系统的任务调度方法对车间生产效率和AGV 有效利用率有重要影响。目前国内外对AGV 调度策略方面主要研究方向主在路径规划优化、作业系统的效率优化方向,大多文献均是关于实现以上优化目标的算法及其效率。如:文献[1]提出最小化岸桥操作的延迟时间和自动导引车的总行驶时间,来提高码头的装卸效率[1];文献[2]提出了一种改进的遗传算法进行AGV 任务的分配和路径的优化,通过改进遗传算法的变异算子,提高种群的收敛速度和收敛性[2];文献[3]针对汽车流水线的布局特征,以AGV 小车利用效率最高、数量配置最少为目标建立数学模型,提出了一种改进的两阶段启发式算法[3];文献[4]提出采用改进遗传算法来求解AGV 路径,改进遗传算法具有更快的收敛速度,并且得到最优解的概率更高[4];文献[5]提出以AGV运行时间最短为目标,将多种群遗传算法引入到两阶段路径规划策略[5];文献[6]提出以平均队长和逗留时间作为性能指标,由泊松过程和排队论的基本理论建立M/M/1 排队模型[6];文献[7]以岸桥前小车作业延迟时间和岸桥后小车与AGV 间的等待时间之和最小为目标函数,建立了带有时间窗约束的AGV调度混合整数规划模型[7];文献[8]主要研究AGV 最优调度方案和最佳AGV 数量匹配关系[8],文献[9]提出了以卸船完工时间最小化为目标,提出考虑任务顺序约束的岸桥与集卡联合调度的混合整数规划(MixedInteger Programming,MIP)模型和约束规划模型约束的岸桥与集卡联合调度的混合整数规划(MixedInteger Programming,MIP)模型和约束规划模型[9]。
文献[5]、文献[9]有提到任务排序但未给出明确的排序模型,其他文献均未提到任务排序,然而在太阳能电池片生产现场,由于工序之间严格的先后关系、生产线产量要求、工序产出物料严格的存放时间要求等因素均对AGV 调度策略有决定性的影响,不能简单的以整体物流搬运效率最高为优化目标,因此针对太阳能电池生产线物流任务调度方法研究有重要意义。
本文主要创新点是针对太阳能电池生产线的特点,建立了物流任务排序模型,提出了将任务优化的目标集合从当前所有任务,缩小为不大于该区域AGV 数量的任务,并针对该缩小后的任务集合进行优化,提出了优化目标函数及任务执行时间计算方法,并采用匈牙利算法进行求解,提高了求解效率且降低了优化问题的复杂度。该调度策略相比本项目初期的调度方法提高了生产线产量、保障了工序产出物料不超时、提高了AGV有效利用率。
2 太阳能电池片生产线特点
如图1产线流程图所示,太阳能电池片车间中每条自动化生产线中有15台设备,分别负责10道不同工序,工序与工序之间设有物料缓存区;设备与设备,设备与缓存之间通过AGV 搬运花篮传递物料,花篮中装满了硅片,部分工序花篮中硅片消耗完后需通过AGV将空花篮返回上工序。每个设备有至少一个送料口和出料口与AGV 进行对接传递花篮;当送料口空或出料口满的情况下,每个设备均有少量缓存,如果没有AGV及时将物料运送到该设备或将物料从该设备取出,则该设备不能继续生产,同时每个工序的产出物其可存放时间有明确要求,产线产量以最后一道工序的产出为准。
物流路线有3类:设备到设备、设备到缓存、缓存到设备,所有的物流运送均采用AGV,每台AGV一次只能执行1个物流任务。

图1 产线流程图
3 问题建模
3.1 任务排队模型
由于产线跨度达250m,为提高运输效率,首先对产线进行分区,不同分区的AGV单独调度。
I表示第i个区域,Ri表示第i区域任务排序后的集合;Qin表示是i区域第n个任务的优先级,Qin越大任务排序越靠前;N表示产线工序数量; Tin表示第n个任务的等待时间,γin为第n 个任务超时报警阈值,是一个常量;k 表示任务所在工序段编号;h 表示任务类型。以不因等待产生报废品、生产线产量最高为目标,任务排队应满足以下约束条件:
(a)后工序段物流需求大于前工序段物流需求。
(b)同优先级的任务,按其任务产生时间排序。
(c)超过设置的等待时间最大值的任务优先级高于其他区域内未超时的任务。
(d)连接任务不参与排序:指本任务的终点是某物流任务的起点,在AGV执行完当前分配的任务后,必须立即执行连接任务。
以上规则可用以下公式表示:
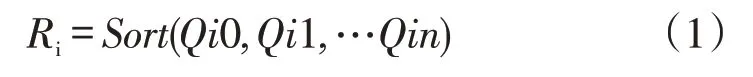
其中
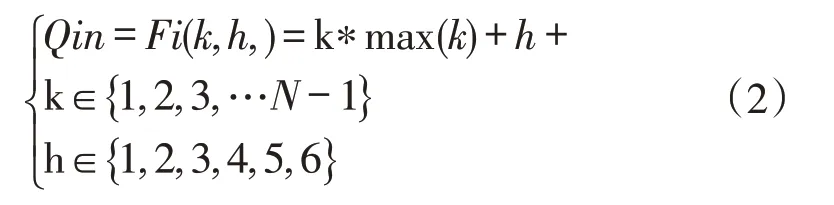
其中
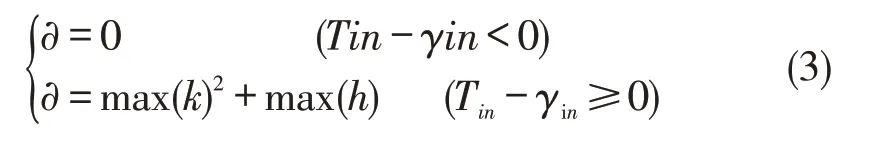
K 表示物流任务属于那两个工序间。如1 表示工序1与工序2之间。
任务类型h值含义:h=1表示上工序机台到缓存;h=2 表示缓存到上工序机台;h=3 表示下工序机台到上工序机台;h=4表示到下工序机台到缓存;h=5表示缓存到下工序机台;h=6表示上工序机台下工序机台。
3.2 分组优化策略及目标函数
由于产线生产过程中异常较多,物流需求有一定随机性,物流任务的排序顺序会随新物流需求的产生在不断变化,因此针对区域内当前所有任务进行最优解求解,不仅需要的时间长,而且也不能保证整体上是最优解,因此在本太阳能电池片生产车间中采用以下策略进行任务调度。
(a)开始执行的任务不再参与任务的分配。
(b)对某区域内物流任务排序,排序后按区域内agv 数量将排名前n 个任务组成一组,要求组内任务执行时间最短.
(c)有新物流任务产生且影响到前n个任务排序时,重新进行任务分配。
Taskk表示排序后某区域内的第k个物流任务,i为该区域内agv 小车数量,该区域内任务分配的对象可用以下集合表示:

为保障物流任务执行效率,以i个agv执行k个物流任务时其所用时间最短为目标,优化目标函数可用以下公式表示:

Tik表示:第i个AGV执行第k个任务所时间。
3.3Tik计算
设某区域有i台AGV,k个物流任务(如果k>i则按先产生先服务和分组策略选前i个产生的物流任务),每个agv执行第k个物流任务所需时间:
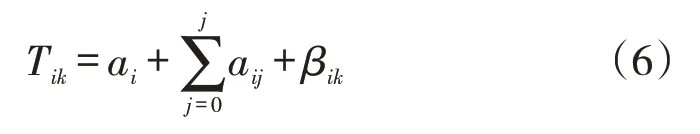
其中ai表示第i个agv执行完当前任务所需时间,如果agv当前没有任务则∂i=0,否则:

其中Δi1表示agv由当前所在位置到上货点并取到货所需时间;Δi2表示由上货点到下货点并送完货所需时间;如果agv已取到货,则Δi1=0,Δi2表示当前所在位置到下货点并送完货需时间,Δi1、Δi2的计算是方法是根据“迪杰斯特拉”算法获取从P1点到Pn所需经过的所有点,那么可依据点的坐标得到agv小车实际需要行驶的距离,用函数Dis(P1,P2,...,Pn)表示。因此第i辆agv到达目的地Pn所需时间如下,γ表示花篮传输时间,是一个常量:
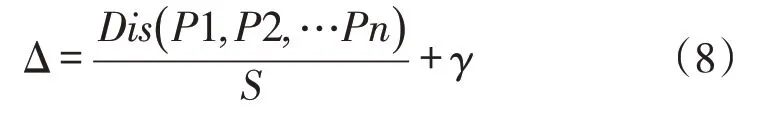
βik表示第i个agv执行第k个任务所需时间:

其中Δi3表示agv由执行完上一次任务后所在位置到上货点并取到货所需时间;Δi4表示由上货点到下货点并送完货所需时间,其计算方式与Δi1、Δi2的计算方式一致。
4 匈牙利算法介绍
1955年,库恩提出了指派问题解法,该方法以匈牙利数学家康尼格提出的关于矩阵中0元素的定理为基础,因此得名匈牙利法。该解法中指出,指派问题最优方案就是要在n阶系数矩阵中找出n个分布于不用行不同列的元素使得他们的和最小。
匈牙利算法的本质是通过对n阶系数矩阵进行变换使得矩阵中的独立0元素与矩阵的阶数一致,然后将系数矩阵中的所有独立0元素都变成元素1,而其他元素均变成0元素,得到的新矩阵便为原指派问题的解矩阵,根据解矩阵中0元素所在的行、列数,就可确定最优的任务分配组合。
独立0 元素指该0 元素所在的行和列中不能再有其他的独立0元素。
5 算法验证
假设i=3,k=2,AGV1当前坐标点是P0,AGV2当前坐标点是P4,AGV3当前坐标点是P11,有2个待执行任务,从P2至P3,P8至P9,所有agv当前均没有执行任务,因此由于i<k,因此不用对任务排序,直接进入分组优化。
根据“迪杰斯特拉”算法计算,AGV1(编号78)、AGV2(编号76)、AGV3(编号75)执行物流任务时的路径如图2、3、4 所示,路径中点的坐标见表2,agv 速度S=0.5m/s,每次对接时间γ=30s,由公式(6),(7),(8),(9)可计算出AGV1和AGV2按执行任务时各自需要的时间见表1:
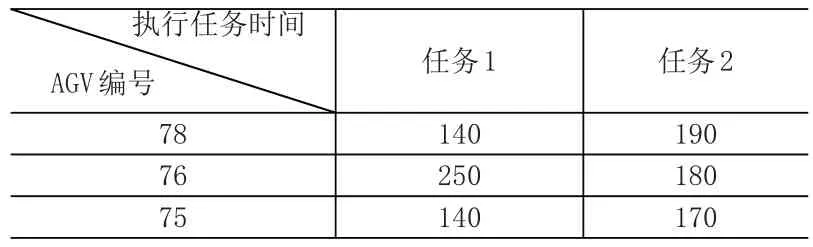
表1 AGV执行任务时间
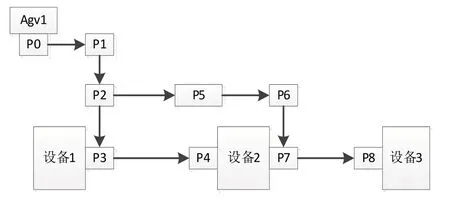
图2 AGV1路径
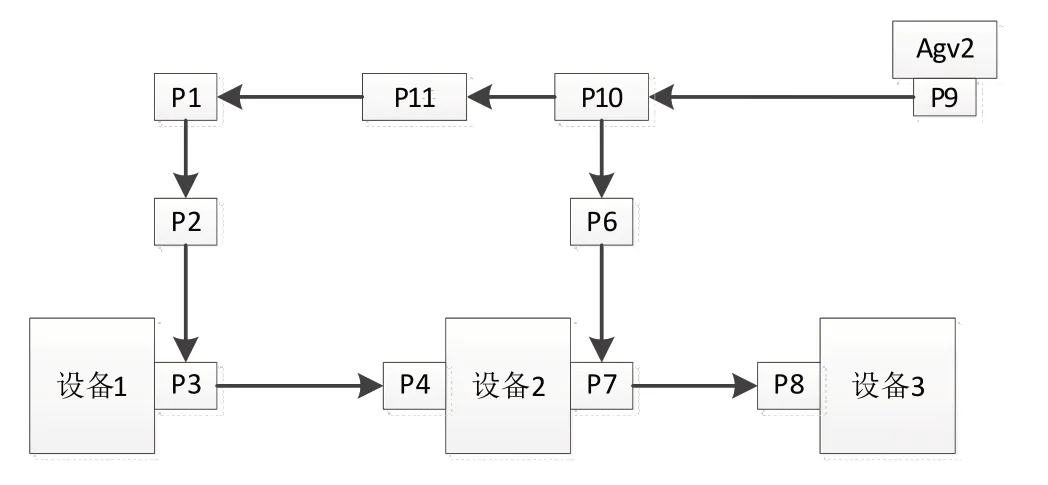
图3 AGV2路径

图4 AGV3路径
以每个agv 执行每一个任务所需时间作为矩阵的1行,构建如下所示待求解矩阵。
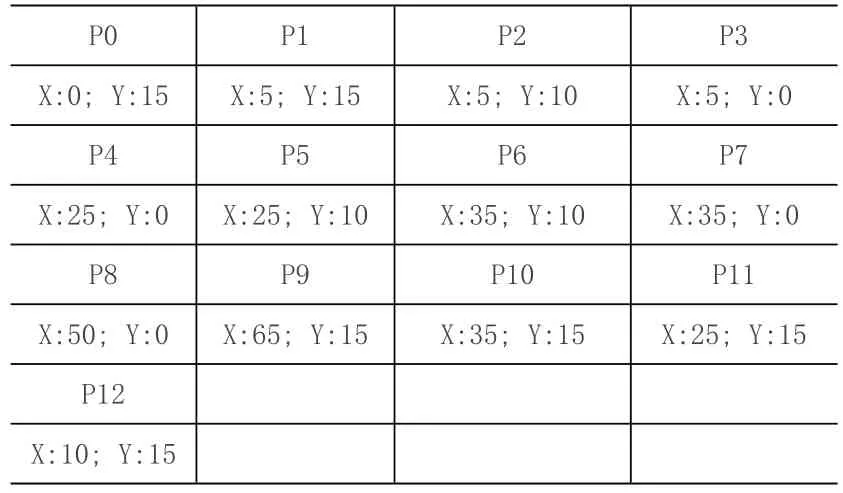
表2 各路径点坐标
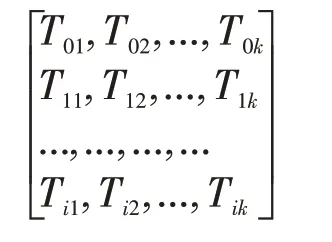
由于匈牙利算法只支持对n阶该矩阵(行数与列数相等)进行变换,因此需采用补充i-k 个虚拟物流任务且每个agv 执行时间均为0 的方式,从而得到该问题的待求解矩阵如下
采用匈牙利算法对其进行求解,其过程及结果如下,如图5所示:
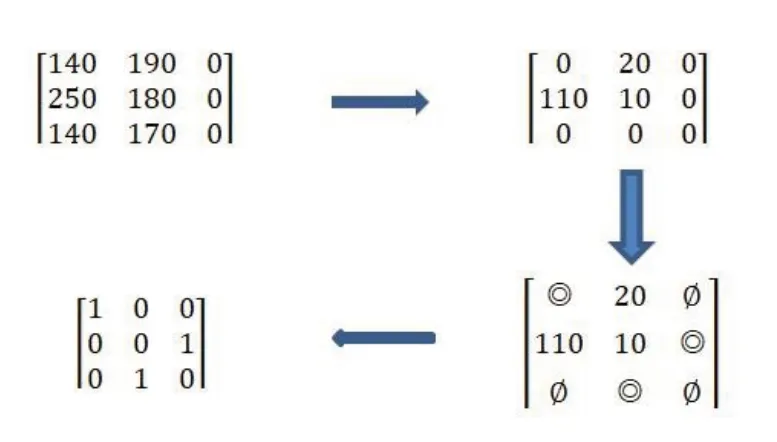
图5 矩阵变换过程
为独立0元素,第三个矩阵的独立0元素的个数等于矩阵阶数,因此将独立0元素改为1,独立0元素以外的其他元素全部改为0,即可得到最优解矩阵,并通过该矩阵可知最优分配方案为:由AGV1执行第1 个物流任务,AGV2 执行第3 个虚拟物流任务,AGV3执行第2个物流任务。最优分配方案下执行完所有任务所需最少时间为:

由于i,k 均较小,可直观看出该算法的结论是正确的。
6 效果对比
本项目最初分配算法是:任务按任务产生时间排序,定时循环未分配任务列表,然后循环计算每个AGV执行该任务的时间,将时间最小的agv分配给任务,当不同AGV执行统一任务时间相同时,采用随机分配法,选择AGV编号最小的。
如图2所示,针对本文“算法验证”一节的案例,按原算法,取时间最少的AGV,若时间一致则按AGV编号排序,取编号最小的AGV,因此其分配的方案为:
75 号车执行任务1,76 号车执行任务2。该方案任务执行的总时间为:
140+180=320>310 采用匈牙利算法得到的任务总执行时间)
因此原有任务分配算法效果不及匈牙利算法;其次任务按时间排序不能满足产线产量最高、工件不超时的原则,因此本文提出的任务调度策略以及优化方法比原始的策略和算法更优。
7 程序实现逻辑及应用案例
图6是系统实现该调度策略和算法的程序逻辑流程图,图7所示是应用了该任务分配方法的调度系统软件。该调度系统是成都四威高科技产业园有限公司针对光伏行业研发的智能物流调度系统。
8 结论
本文所述的AGV调度策略在保证生产车间产量的条件下,有效提高了该太阳能电池片生产车间的物流效率。本文排序模型考虑的约束条件只有工序顺序,连接任务,是否超时,复杂应用中约束将更多且不能与后端的执行优化分割开来看,下一步将着重研究多约束条件下为使得产线产能最高,如何进行任务排序和选择优化策略。
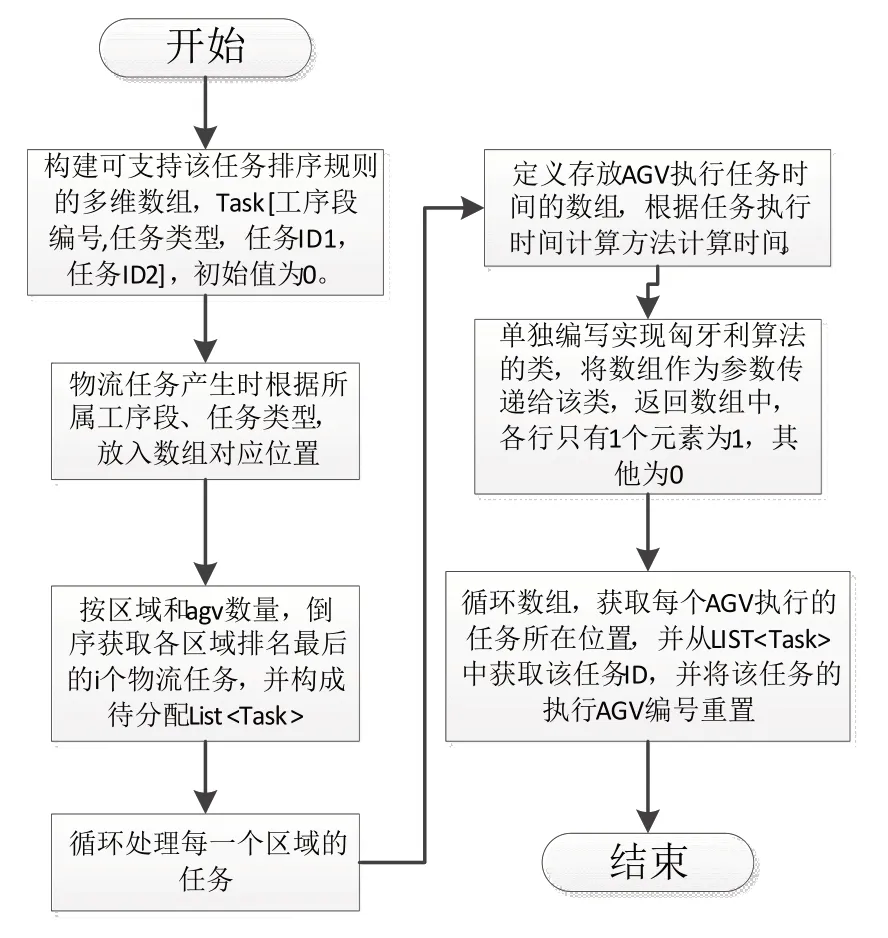
图6 程序逻辑流程图
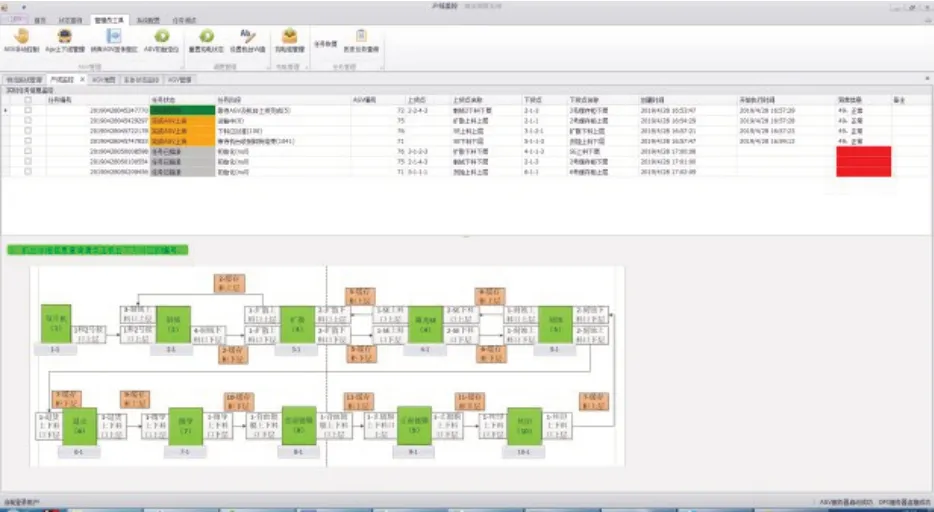
图7 AGV调度系统界面
