基于全息干涉图的物体三维面形重建算法

文/刘温彦

1 引言

三维面形测量在目标检测、产品检验、材料分析、生产制造、文物修复等领域具有广泛应用。目前的形貌测量分为两大类：接触式测量和非接触式测量，非接触式测量方法即在不接触被测物表面的条件下，可以得到被测物体参数的测量方法，具有测量速度快、精度高、实时、非接触等优点。目前主要分为电磁学、声学、光学三大类。基于光学原理的测量方法具有抗电磁干扰、可以微区隐蔽测量等优点，被广泛应用于各行各业。其中常用的主要有数字全息法、时间飞行法、相位测量法、莫尔条纹法、结构光法、散斑干涉法、双目及多目立体视觉法等。不同方法针对不同的测量场合，各有优缺点。本文采用高精度、非接触式迈克尔逊干涉法对物体表面进行三维测量。

2 理论建模

本文所采用的迈克尔逊干涉装置如图1所示，激光管LD发出的激光束经扩束系统扩束后，由半反镜BS分为两束-反射和透射光束，反射光束经反射镜M反射形成参考光束，透射光束入射到待测物体表面，由物体反射后即为物光束，两束光干涉后光强由CCD摄像头接收，送入计算机进行图像处理和面形重构。

假定LD发出的是一束平行光（平面波），则参考光束和物光束的复振幅分别表示为：

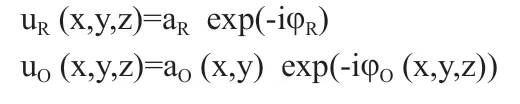
图1：干涉装置，LD：激光管；BS：半反镜；M：反射镜；M1：M相对于BS的对称位置；CCD：摄像机；PC：计算机

其中aR和φR分别为参考光束的振幅和位相，aO(x,y)和φO分别为物光束的振幅和位相。如果物体表面起伏用z(x,y)表示，那么CCD所接受到的干涉光强为：

3 不同物体表面的二维干涉图

根据上述理论模型，我们针对不同形状的物体表面（包括平面、凹球面及凸球面）进行理论计算，可以得到不同的二维干涉条纹图。

如果物体表面为平面，并且与系统光轴（z轴）垂直，则z(x,y)为常数，无干涉图案。如果物面是与M1（镜面M关于BS的对称面）夹角为θ的平面，则物光、参考光位相差表示为假定aR=aO(x,y)=1,λ=0.405μm，θ=18°，并将它们代入方程（1），我们可以得到平面物体二维干涉条纹分布如图2a所示。从图中可以看到，干涉图是一系列平行直条纹，条纹的间距跟倾角θ有关。

当待测面为凸面时，物、参考光的位相差为φO-φR=2k[z(x,y) ]=2k[L-(x2+y2)/2R]，将此式及aR=aO(x,y)=1,L=3μm,R=10μm,λ=0.405μm代入方程（1）可得干涉图如图2b所示，从图中可以明显看出，干涉图是同心圆环，中心为暗纹，而且环间距从中心到边缘逐渐减小。

当待测面为凹球面时，物光与参考光位相的不同表示为φO-φR=2k[Lz(x,y) ]=2k[L-(x2+y2)/2R]，将此式及aR=aO(x,y)=1,L=0,R=10μm,λ=0.405μm代入方程（1）可得干涉图如图2c所示，从图中可以明显看出，干涉图同样是同心圆环，而且环间距也是从中心到边缘逐渐减小。与凸面所得干涉图不同的是中心为亮干涉场，这是因为中心位置条纹的光强与物体表面开口和M1的间距L有关。

4 面形重建

如果图1中CCD所采集到的干涉图的光强分布为I(x,y)，对此光强进行信息处理和解调重建物体的三维表面形貌。步骤如下：首先我们对光强I(x,y)进行菲涅尔近似或者菲涅尔变换，得到如下方程：

其中d是重构表面和CCD摄像头之间的距离，uR*(x,y)为参考光束的复共轭光束，λ为LD激光的波长。由此式子计算出Γ(ξ,η)后，我们可以得到物体表面的光强（振幅）分布及位相，表示为：

角度函数的分子和分母分别表示函数Γ[ξ,η]的虚部和实部。

图3a是一个任意表面物体的二维干涉条纹图，从图中可以看出，该图是关于y轴基本对称的图形。图3b是利用上述方法，将参数d设为与L同量级的常数，将参考光复共轭光束uR*(x,y)设为常数（因为参考光是平面波），代入公式经过计算解调后，重新构建的物体的三维表面形貌图，从图中可以明显的看出该物体表面是关于y轴对称的曲面。

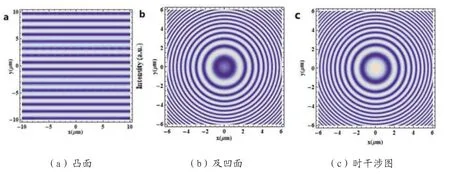
图2：物体为平面

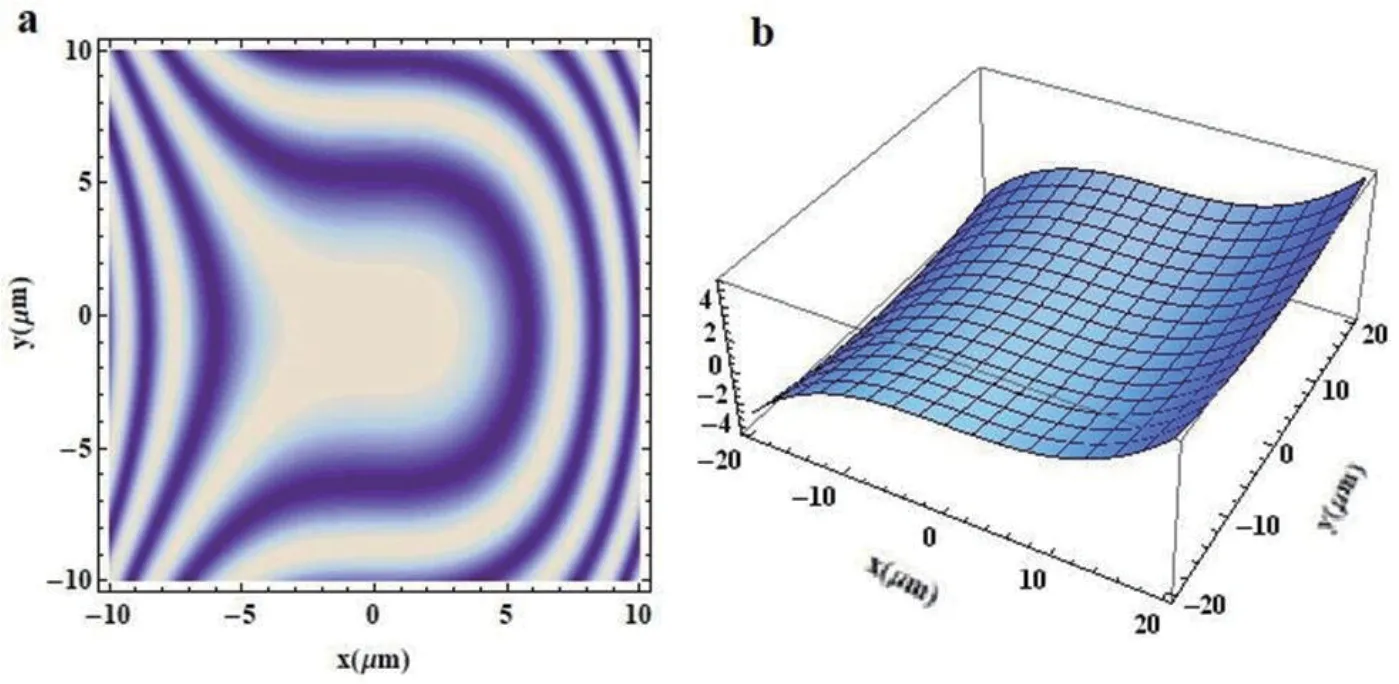
图3：任意曲面干涉条纹图（a）及重建的三维表面形貌（b）

5 结论

本文利用迈克尔逊干涉装置及双光束干涉法建立物体表面形貌测量的二维干涉模型，并以平面、凹球面和凸球面为例，给出相应的干涉光强分布图，他们分别为平行直条纹图、同心圆环图，而且条纹间距与平面和光轴夹角有定量关系，圆环间距与球面半径的大小有关。最后给出三维形貌重构的理论模型，并以任意曲面干涉强度分布为基础，采用菲涅尔近似或者菲涅尔变换的方法给出物体表面的振幅和位相，从而重建出物体表面三维形貌。文中涉及方法简单、实时性好，对于面形的非接触、高精度测量具有重要的应用前景。