单晶锌电极在应变电荷耦合下的溶解机制-跨尺度计算与机器学习
2020-01-17蒋红星孙俣哲张统一
蒋红星 孙俣哲 孙 升 张统一
(上海大学材料基因组工程研究院,上海 200444)
20世纪以来,金属材料的使用量急剧增长,其开采冶炼加工过程消耗了大量的能源,每年因为电化学腐蚀造成了大量金属材料的浪费,所以金属的腐蚀溶解问题得到了广泛的关注。金属电极的腐蚀受应力应变和电化学环境的影响,因此有必要研究应变-电荷耦合场下金属电极的腐蚀特性。Gutman等[1]研究发现,外加力场会导致金属材料电化学势的改变,在金属电极发生弹性变形时,随着拉伸/压缩应力的增加,金属的开路电压呈线性降低的趋势。这是由于力学化学作用使应变能转变为电化学能,即金属的表面活性增大,腐蚀倾向也增大。国内关于应变腐蚀的研究报道[2-3]也很多,如 Zhang等[3]研究了拉应力作用下X80钢在酸性溶液中的电化学行为,发现随着拉应力的增加,电极的开路电位降低,反应活性增加。Mavrikakis等[4]通过密度泛函理论(density functional theory,DFT)研究了应变对金属电极表面反应活性的影响,计算中对Ru(0001)晶面施加面内应变,发现表面应变与O原子/CO分子的吸附能和活化能垒之间存在关联性,相对于无应变表面,拉伸应变表面降低了对O原子/CO分子的吸附能以及CO分解过程的能垒,并将这种效应归因于金属d能带中心随应变的变化。
锌具有蕴藏量丰富、低毒、无污染、高能量密度以及低成本等特点,而被广泛用作电池负极材料。其中可充电锌离子电池(zinc-ion battery,ZIB)由于其良好的环境兼容性、极高容量密度、低廉的价格和很高的安全性,被认为是今后大规模能量储存的方向之一[5-6]。镀锌是一种牺牲阳极保护阴极的电化学防腐蚀方法,其工艺成熟、成本较低,被广泛应用于制造业[7]。
但目前的试验方法无法从微观层面研究腐蚀过程中原子的溶解和电荷的转移过程,而跨尺度计算则可以通过原子计算结合宏观溶液计算较好地模拟锌的电化学溶解。Schwarz等[8]通过使用耦合密度泛函理论/连续介质溶液方法,在宽电压范围内的密集计算,揭示了吸附在金属晶体台阶边缘上水的部分氧化机制。本文选择密度泛函/连续介质溶液方法,对锌电极的溶解腐蚀过程进行了详细研究,并结合符号回归算法预测了锌电极发生溶解腐蚀的临界电极表面应变-电荷组合。
1 数学建模与方法
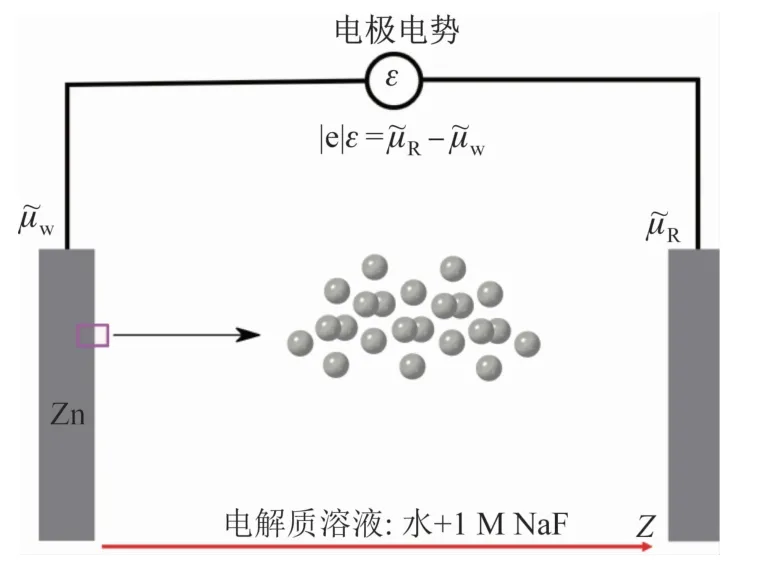
图1 电极/溶液模型和锌电极/溶质锌原子结构示意图Fig.1 Schematic of the electrode/solution model and zinc electrode/solute zinc atoms
计算系统在整个电化学回路中的位置如图1所示,电极为Zn,并浸入含NaF的电解质溶液中。电极使用DFT计算,电解质溶液采用连续介质模型计算[9],计算采用超胞方法。电极模型采用了22个Zn原子,其中20个原子形成一个含有5层原子的平板电极(每层有2×2个Zn原子),另2个锌溶质原子分布在平板的两侧,形成对称结构,如图1中的插图所示。Zn电极与电解质溶液接触的表面方向为密排六方晶格的<0001>方向,[0001]方向被定义为 z轴,Zn电极最外层的原子面则位于z=0。电极两侧填充电解质溶液,超胞沿z向的长度被设定为44.8Å,电极厚度为10.28Å。
本文使用开源软件 JDFTx[10-13]进行密度泛函/连续介质溶液耦合计算,电解质溶液模型采用SaLSA模型,该模型具有非局域介电响应特性[9],对电解质溶液中强极化和带电溶质的计算的准确度较高。使用浓度为1 M的隐性Na+和F-离子为锌电极提供徳拜屏蔽效应。DFT计算采用平面波展开,平面波矢空间的K点网格划分为12×12×2,截断能量设定为707 eV,并采用周期性边界条件,交换关联函数使用广义梯度近似(general gradient approximation,GGA)[14],锌 原 子 使 用Ultrasoft赝势方法[15]。电极的电子态密度计算使用线性四面体插值方法[16]。
计算前先进行结构优化,计算步骤如下:(1)将建好的Zn电极模型去除2个溶质原子后放入溶液中进行晶格参数优化(即整个结构处于能量最小化),得到Zn电极HCP结构的平均晶格参数为:;(2)将两个溶质Zn原子放入第1步的结构两侧进行能量最小化(第1步中的结构保持固定,仅松弛2个溶质原子的位置),溶质原子会吸附在锌电极表面3个相邻Zn原子的几何中心上方。在之后一系列计算中电极的晶格参数和溶质原子在平行于电极表面内的位置都保持不变,改变溶质Zn原子与电极表面的距离(从 z=1.55Å至 z=14.65Å)进行一系列能量计算。在密度泛函计算中,金属表面的应变通常是通过改变表面方向的晶格参数来实现的[4,17-19],本文也采用该方法,即通过同时改变晶格a和b方向的参数来施加面内应变。

DFT计算时将净电荷施加在锌电极上,因此净电荷位于电极和2个孤立Zn原子中。表面电荷由电极最外表面原子的电荷密度相对于电极内部原子的电荷密度的变化来定义,通常使用吉布斯突变表面模型,定义为表面每单位表面积的净电荷。为了区分这两类净电荷,将整个计算系统的净电荷简称为净电荷,而表面的净电荷称为表面电荷。净电荷是由施加的电位引起的,而表面电荷是由自由表面引起的。表面电荷随净电荷的变化而变化。
密度泛函/连续介质溶液计算中分别使用自洽场(SCF)和Polak-Ribière共轭梯度法进行电子和电解质的弛豫。在两次连续的SCF自洽循环中,能量收敛的相对准确度被设定为10-7Hartree(1 Hartree≈27.211 4 eV)。采用 Löwdin电荷布居分析[21-22]计算电极和溶质Zn原子的电荷分布。
由于计算Zn溶解/吸附的临界(净电荷、电极面内应变)组合需花费较多时间和成本,因此基于机器学习中的符号回归算法(symbolic regression)[23-24],找出拟合训练数据的函数关系式,然后利用函数关系式,求得具有给定性质的参数组合,进而加速寻找临界净电荷-电极表面应变组合。
2 结果和讨论
为了计算方便,采用22个锌原子的净电荷总值表征系统的净电荷。图2(a)和图2(b)分别是在净电荷为3.5|e|和4.0|e|时,不同电极面内应变下能量随电极-溶质原子距离的变化(图中实线表示使锌溶质原子自动溶解的应变)。能量Ead的定义为:
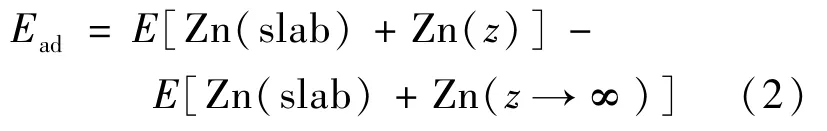
式中:E[Zn(slab)+Zn(z→∞)]表示计算系统的能量,此时溶质锌原子远离电极表面,Zn(z→∞)]由 Zn(z=14.7Å)近似,在 z≥7Å时溶质锌原子和Zn电极之间的相互作用可忽略不计。
如图2(a)所示,在净电荷为 3.5|e|、未施加应变的条件下,在2.46Å<z<4.5Å范围内,系统能量处于1 eV的平台,即在此范围内溶质原子的溶解/吸附近似处于平衡状态。在电极面内施加5%拉伸应变时,在1.6Å<z<4.5Å范围内出现了一段能量峰值,即从2.46Å处的能量低点(电极表面的吸附位置)到4.5Å处的能量高点,约0.17 eV的能量势垒,该势垒会阻碍溶质原子溶解进入电解质溶液。在电极面内施加 -5% 应变(压缩应变)时,吸附能单调递减,说明表面溶质原子产生了自发溶解。z>4.5Å时,不同应变下系统能量均不断降低,当z>6.9Å时基本稳定,表明溶质原子在远离电极表面时与电极间的相互作用微弱,而在4.5Å<z<6.9Å时能量明显降低,说明溶液中的溶质原子将难以跨越能垒而传递到电极上。如上所述,(3.5|e|,0)为一组临界组合(电荷,应变)。
如图2(b)所示,在净电荷为 4|e|、未施加应变的条件下,系统能量随溶质原子-电极表面间距增加而单调减小,说明表面溶质原子产生了自发溶解,且这一过程不可逆。在电极面内施加5%和15%拉伸应变时,在2.46Å<z<4.5Å范围内,能量下降坡度随着拉伸应变的增加逐渐减缓,此处能量坡度定义为溶质原子从z=4.5Å进入到吸附位置z=2.46Å时的能量势垒,该值在0%、5%和15%应变下分别为1.02、0.63和0.11 eV。在施加20%拉伸应变时,能量坡度为负值,在z=2.46Å时最低为0.61 eV,在z=4.5Å时最高为0.82 eV,能量势垒为0.21 eV,阻碍溶质原子进入电解质溶液。在z>4.5Å范围内,能量变化趋势与图2(a)的相似,4.5Å<z<6.9Å范围内的能量坡度阻止了溶质原子吸附到电极表面。
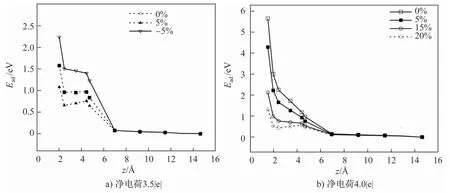
图2 不同净电荷下能量随电极面内应变的变化Fig.2 Energy profiles of zinc atoms on a zinc electrode under different surface strains at different net charges
图3(a、b)和图 3(c、d)分别是在净电荷为3.5|e|和 4.0|e|时,不同电极面内应变下溶质 Zn原子和电极最外表面锌原子所带电荷随电极-溶质原子距离的变化。图3(a)中,溶质原子的最大电荷均出现在z=4.4Å时,在0%、5%、-5%应变下该数值分别为 1.65|e|、1.53|e|和1.76|e|。在[1.6,4.4]Å范围内,不同应变下每个溶质Zn原子所带电荷均随着电极-溶质原子间距的增加而增加,如在5%拉伸应变下,溶质原子所带电荷从1.11|e|增加到1.53|e|。图3(b)中,在[1.6,4.4]Å距离范围内,不同应变下电极最外表面每个锌原子所带电荷均随着电极-溶质原子间距的增加单调减少,在0%应变下,锌原子所带电荷从0.32|e|减小到 0.07|e|,5%应变下从0.19|e|减小到 0.08|e|,在 -5%应变下从 0.16|e|减小到0.03|e|。当z>6.9Å时,在压缩应变和无应变条件下,电极最外表面锌原子所带电荷接近,约0.09|e|,在拉伸应变下,约 0.11|e|。
图3(c)中,随着拉伸应变的增加,溶质锌原子所带电荷降低,如在z=6.9Å,电极面内拉伸应变为0%、5%、15%和20%时,溶质锌原子所带电荷分别为 1.89|e|、1.81|e|、1.63|e|和 1.53|e|。图3(d)中,在[1.6,3.4]Å范围内,0%应变下,电极最外表面锌原子所带电荷最高,如在z=2.56 Å时为0.23|e|,5%、15%、20%应变下分别对应为0.17|e|、0.18|e|、0.19|e|,该结果与图 3(b)中相似,即应变导致在[1.6,3.4]Å范围内电极最外表面原子所带电荷下降,但拉伸应变的增加导致电荷升高,压缩应变的增加导致电荷下降。在z>4.4Å时,随着拉伸应变的增加,最外表面原子所带电荷升高且随着溶质锌原子与电极表面距离的增加基本不变,如在 z=6.9Å时,0%、5%、15% 和 20%下分别为 0.07|e|、0.10|e|、0.12|e|、0.13|e|。结合图2与图3(a)和3(c)中的实线部分,可见在3.5|e|净电荷和-5%应变、4.0|e|净电荷和 0%应变、4.0|e|净电荷和 5%应变、4.0|e|净电荷和15%应变条件下,溶质锌原子溶解进入电解质溶液所带电荷分别为1.45|e|、1.89|e|、1.81|e|、1.63|e|,比较能量曲线发现,溶质原子所带电荷越接近经典理论的+2价态,溶质Zn原子越易溶解。
为了寻找净电荷4|e|下溶质锌原子溶解的临界应变值,使用SR进行符号回归训练,图4显示了在净电荷为4|e|时,不同溶质原子-电极表面距离和拉伸应变条件下系统能量的符号回归数值模型。将训练过程中的4组数据(共40个,图4中黑色数据点)均作为训练集,每个数据包含了溶质原子-电极表面间距与电极面内应变2个特征量和1个系统能量输出量。使用 gplearn(https://gplearn.readthedocs.io)中的符号回归模块对归一化后的数据集进行训练,符号回归模型使用的参数有:population_size=5000,迭代次数(generations)为 113,计算精度(stopping_criteria)设置为0.008,交叉概率(p_crossover)为0.7,子树变异概率p_subtree_mutation=0.1,hoist变异概率p_hoist_mutation=0.05,点变异概率p_point_mutation=0.1,最大样本抽取 max_samples=0.9,过程打印 verbose=1,稀疏系数 parsimony_coefficient=0.000 12。根据图4中符号回归训练模型,在[0%,20%]应变范围内等间距取100个应变值并代入图4的符号回归模型,比较发现在应变为16.75%时,溶质原子在电极表面的溶解/吸附最接近于临界状态。

图3 在净电荷为3.5|e|和4.0|e|时,不同电极面内应变下溶质Zn原子和电极最外表面锌原子所带电荷随电极-溶质原子距离的变化Fig.3 Charge curves of solute zinc atoms and zinc atoms on the outermost surface of electrode as a function of distance from electrode to solute atoms under different electrode surface strains when the net charges are 3.5|e|and 4.0|e|

图4 净电荷为4|e|时的符号回归训练模型Fig.4 Symbolic regression trainingmodel under net charge of 4|e|
为了验证SR预测的临界组合(电荷,应变)的准确性,进行了净电荷为4|e|、电极面内应变为16.75%条件下的计算。如图5所示,实线为符号回归模型预测值,方块为采用JDFTx计算的电极表面应变为16.75%时的数值,可见计算值与符号回归模型预测值基本吻合,说明了符号回归模型的预测精度较高。在2.46Å<z<4.5Å范围内,模型预测值和计算值都为0.61 eV左右,没有出现能量势垒,即溶质原子在吸附位置处于临界状态。在z>6.9Å时,两者均逐渐稳定,说明符号回归模型可以预测溶质原子进入电解质液后与电极表面微弱的相互作用。结合JDFTx计算和符号回归的预测值,得到了两组溶质原子溶解/吸附临界组合(电荷,应变),分别为(3.5|e|,0%)和(4|e|,16.75%)。从图中还能看出,当电荷小于6.9Å时,另外两组以电极表面应变为自变量的曲线的应变值存在差异,而在z>6.9Å后逐渐与电极表面应变16.75%时的曲线重合,并趋于稳定,与上述解释相符。

图5 符号回归算法预测曲线和JDFTx计算值Fig.5 Curves predicted by using symbol regression algorithm and values calculated by JDFTx
3 结束语
本文使用密度泛函/连续介质溶液模型耦合计算研究了应变-电荷耦合场下Zn电极的溶解机制。在净电荷3.5|e|下分别在电极表面内施加了5%(拉伸)和-5%(压缩)应变,锌电极表面溶质原子的近似溶解/吸附平衡状态被打破,施加5%应变抑制了溶质Zn原子的溶解,而施加-5%应变则促进了溶质Zn原子的溶解。此外,在系统净电荷为4.0|e|以及施加不同拉伸应变的条件下,拉伸应变越大抑制作用越明显,直至出现能量势垒阻止了溶质Zn原子的溶解,且拉伸应变的增加导致溶质Zn原子进入电解质溶液所带电荷也下降。结合JDFTx计算值和符号回归模型,可以预测固定净电荷下Zn电极表面溶质原子溶解/吸附平衡状态的临界应变。但是本文计算得出的拉伸应变抑制溶解的结果与通常认知不符,可能的原因是通常试验采用的是宏观多晶材料,而本文计算的是一种完美单晶金属材料。
