一种新的三孔探针试验数据处理方法
2020-01-17吴晓东王迎国刘志刚吴舒娴
吴晓东,王迎国,刘志刚,吴舒娴
(中国航发四川燃气涡轮研究院,四川绵阳 621000)
1 引言
作为一种有效的测量气流特性的装置,多孔探针具有经济性好、使用方便、可靠性高及便于维修等优点,常用于航空发动机内部流场测试领域[1-3]。三孔探针适用于二维流场或仅需测量二维特性的三维流场,如平面叶栅和涡轮导向器出口流场等,且测试中常采用非对向法,即测试中探针不转动,根据三孔压力和标定风洞中获取的标定系数进行数据处理,以得到被测流场参数。
国内外学者对三孔探针数据处理方法进行了大量的研究。Treaster等[4]使用样条插值法进行数据处理,验证了样条插值法的有效性;金捷等[5]采用最小二乘法对标定和实测数据进行处理,角度和速度偏差均满足工程上三维流场测量的要求,具有较高的工程实用价值;钟兢军等[6]成功应用最小二乘法生成标定系数与流场参数之间的显式关系进行风洞流场自动化测量;廖安文等[7]在最小二乘法处理中引入表征马赫数变化的系数,提高了数据处理精度;Rediniotis 等[8]将BP 神经网络法应用于多孔探针的数据处理中,王洪伟等[9]采用理论模型初步验证了神经网络法的精度与效率。
目前的流场试验中,对数据处理方法的精度和效率要求均较高。工程中常采用的样条插值法和最小二乘法,其处理精度均能满足工程使用要求,但由于二者需要不断地进行速度迭代,总体处理效率较低,无法满足实时处理的要求。而神经网络法需要依靠专用数值计算软件,利用软件内置神经网络函数生成并训练神经网络,仅能用于后处理。为此,在三孔探针数据处理常用方法的基础上,本文提出一种新的数据处理方法——相交曲线法,该方法在保证样条插值法和最小二乘法处理精度的前提下可更高效地处理流场数据。
2 三孔探针标定
按头部结构,三孔探针可分为圆柱型、楔型和锥型探针,如图1所示(图中数字为测压孔编号)。
三孔探针的标定在常温风洞中进行。一般流程为:将探针安装在风洞出口的角度位移机构上,测取不同马赫数Ma和角度α下的三孔压力数据p1~p3、风洞进口总压pt、风洞喷口壁面静压ps。4 个标定系数——角度系数Kα、速度系数KMa、总压系数Kt和静压系数Ks的计算式见式(1)。
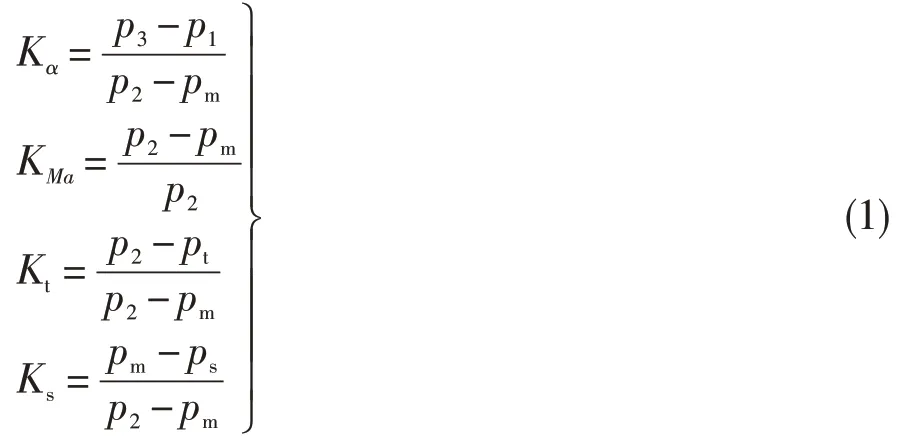
式中:pm=(p1+p2)/2。
3 样条插值法和最小二乘法处理流程
获取标定系数后,根据三孔压力即可进行数据处理。数据处理过程中,样条插值法和最小二乘法的核心思路一致:①根据试验中某测点三孔压力p1c~p3c,采用式(1)计算出该测点的角度系数Kαc,继而算出各马赫数下的角度;②根据样条插值或最小二乘拟合的方式建立马赫数与角度的单值函数关系;③在标定马赫数范围内选取一个马赫数Ma0作为处理初值,然后根据该初值计算出新的马赫数Ma1;④对比二者差值与罚值,判定是否完成迭代,若未完成迭代,则采用二者平均值更新Ma0,继续迭代计算直至完成迭代;⑥输出各流场参数。其具体流程见图2。处理流程中,马赫数初值取值对计算效率影响很大,若真实马赫数远离初值,则迭代次数会增加,致使计算效率下降。
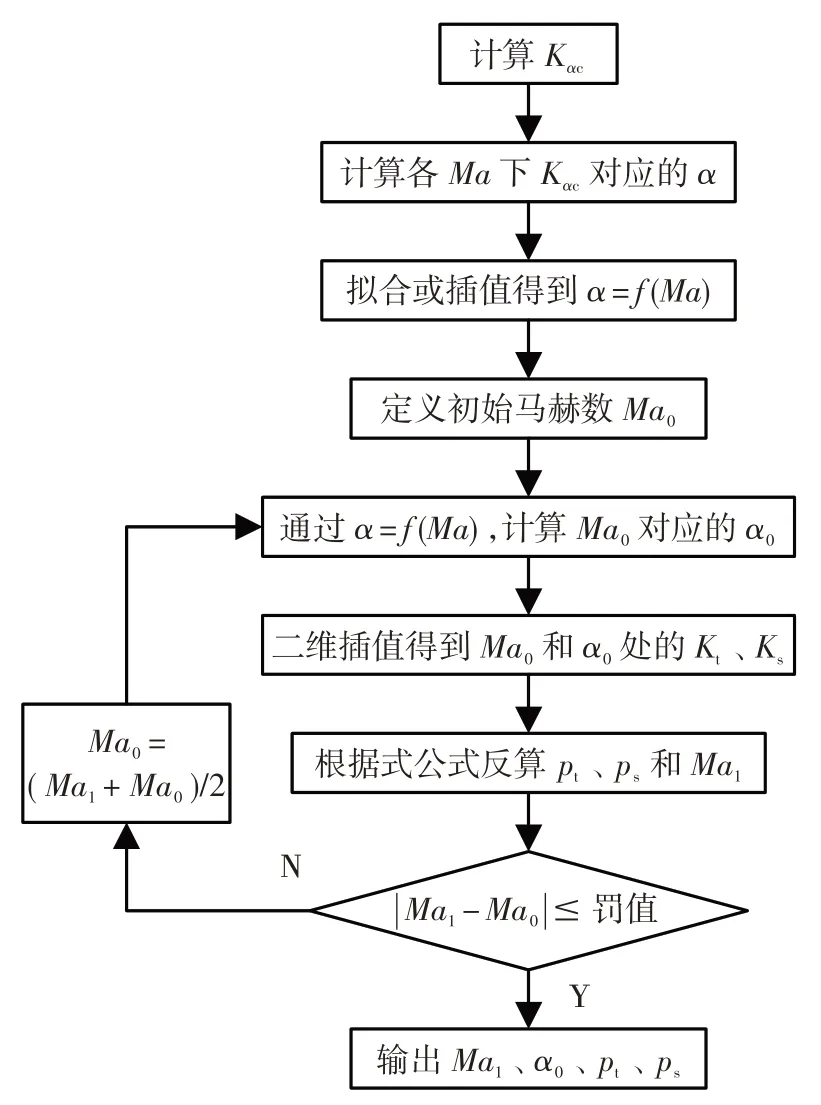
图2 数据处理流程Fig.2 Flowchat for data processing
4 相交曲线法原理
数据处理过程中,样条插值法和最小二乘法仅使用了角度系数、总压系数和静压系数,未使用速度系数。由速度系数计算公式可知,其近似代表动压头与总压的关系,与马赫数存在相关性,类似于角度系数与角度的相关性。图3、图4分别为某锥形三孔探针的速度系数和角度系数在标定范围内的分布。由图可知,各角度下速度系数与马赫数呈单调递增关系,而各马赫数下角度系数与角度呈近似线性递增关系。样条插值法和最小二乘法仅使用了其中一种关系,本文所提出的相交曲线法则将利用两种关系进行数据处理。
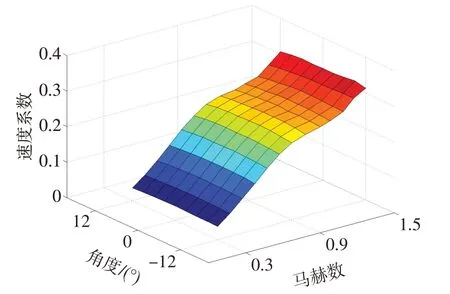
图3 不同马赫数和角度下的速度系数分布Fig.3 Velocity coefficient distribution for different Mach number and angle
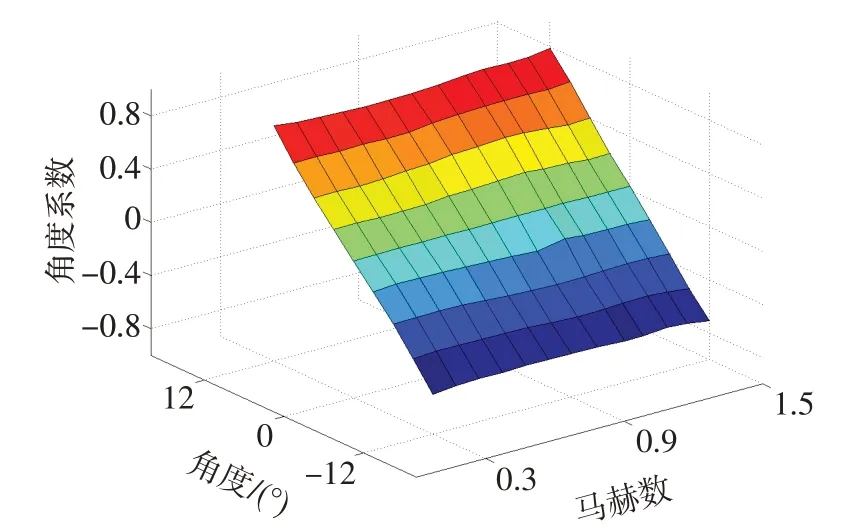
图4 不同马赫数和角度下的角度系数分布Fig.4 Angle coefficient distribution for different Mach number and angle
相交曲线法的数据处理过程如下:根据待处理的三孔压力得到的Kαc,可算出标定马赫数范围内不同马赫数下的Kα0代表的角度,由此计算出的角度和马赫数组成一个点集;该点集可在标定马赫数和角度为坐标的二维平面(以下简称标定平面)上连成一条横跨整个标定马赫数范围的曲线,曲线上所有点处的角度系数均为Kαc,将该曲线命名为角度特性曲线。同理,根据三孔压力得到的KMac,可算出标定角度范围内不同角度下的KMac代表的马赫数,由此计算出的角度和马赫数组成一个点集,该点集可在标定马赫数和角度为坐标的二维平面上连成一条横跨整个标定角度范围的曲线,曲线上所有点处的速度系数均为KMac,将该曲线命名为速度特性曲线。
图5为某测点计算出的角度特性曲线和速度特性曲线,其中红色虚线为标定边界。由图可知,角度特性曲线和速度特性曲线必定在标定平面上产生交点,该交点的坐标即为Kαc和KMac对应的马赫数和角度。根据求出的马赫数和角度,使用二维插值方法计算出总压系数和静压系数,继而计算出总压ptc和静压psc。本文将这种利用两条相交曲线交点处理得到流场参数的方法命名为相交曲线法。通过对某探针所有标定点和非标定点计算得到的相交曲线进行作图发现,所有相交曲线只有一个交点,因此根据相交曲线法原理计算的马赫数和角度具有唯一性。根据该原理,要找这个唯一交点,理论上可通过数值计算或图形图像处理等方式提取交点坐标。数值计算涉及数组的循环计算,图像处理涉及图像保存、像素识别与计算,这两种思路效率均较低。为提高处理速度,本文采用反复迭代的方式寻找曲线交点,具体流程见图6。
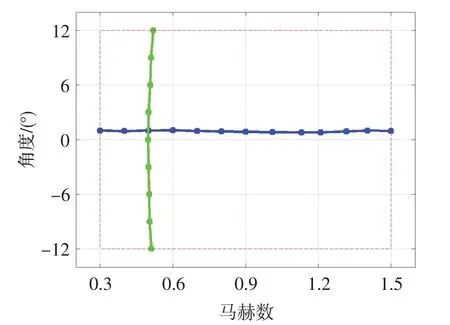
图5 某测点的角度特性曲线和速度特性曲线Fig.5 Angle characteristic curve and velocity characteristic curve of one test point
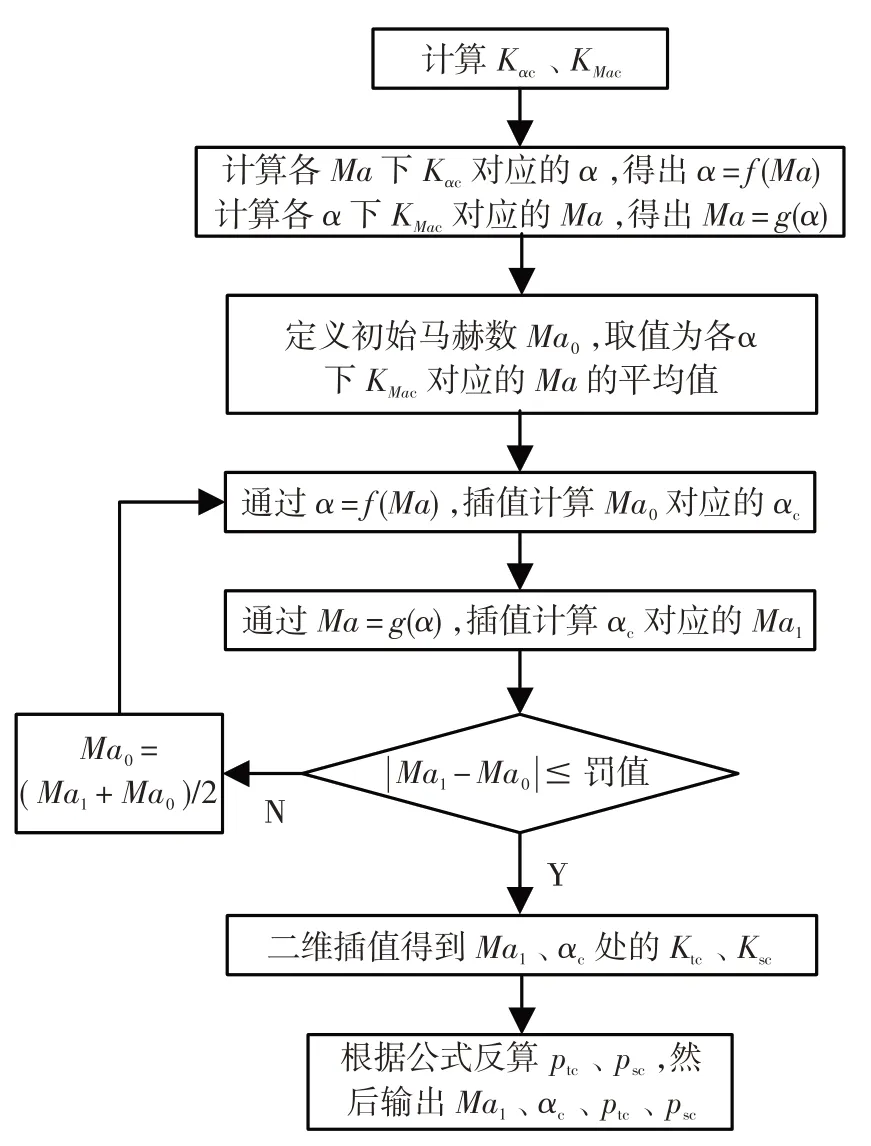
图6 相交曲线法流程Fig.6 Flowchart for intersect curves method
5 方法精度与效率评测
5.1 评测方法
评测相交曲线法、样条插值法、最小二乘法的数据处理精度和效率时,为保证评测结果客观真实,避免编程平台、标定数据和校验数据不同引入的误差,必须使用同一编程平台进行程序编制,必须使用同一标定数据、同一校验数据进行处理。本文采用Matlab 软件编制了三个数据处理程序,分别对应样条插值法、最小二乘法和相交曲线法(以下分别简称插值、二乘和相交),三种方法的马赫数迭代罚值均设为0.001。
工程中,一般采用标定数据作为校验数据进行处理,以验证处理方法的精度。由于样条插值法的核心为插值,插值曲线或曲面总是经过标定数据点。最小二乘法的核心为拟合,拟合曲线或曲面不一定经过标定数据点。而工程中需要处理的试验数据绝大部分不经过标定数据点,故仅采用标定数据作为校验数据进行处理以验证处理方法精度的思路不够全面。可以采用标定数据用于初步验证方法的可行性及精度,而对非标定数据进行处理以校验非标定点精度,这样可更为客观地评测方法的精度。本文选择一组为标定数据,一组为非标定数据,将校验数据的处理结果与校验数据进行对比,综合评测三种方法的数据处理精度。此外,数据处理时还记录了单个测点数据处理耗时,用以评测三种方法的数据处理效率。
5.2 评测结果
将某锥形三孔探针安装在标定风洞出口,调整出口马赫数和角度,测取一组标定数据和一组标定范围内的非标定数据。标定数据包含117 个标定点,马赫数共13个(0.300,0.400,0.500,0.600,0.700,0.800,0.900,1.012,1.131,1.21,1.317,1.403,1.500),角度共9 个(范围为-12°~12°,间隔3°);非标定数据包含78 个非标定点,马赫数范围为0.300~1.500,角度范围为-10°~10°。
图7、图8分别为三种方法每个标定点和非标定点的处理耗时。图9、图10 分别为三种方法得到的标定点处偏差和非标定点处偏差,其中角度偏差为绝对偏差,其他偏差为相对偏差。由图7、图8可知,对于标定数据和非标定数据,各参数下相交曲线法的数据处理效率优于样条插值法和最小二乘法。由图9 可知,对于标定数据,各方法处理得到的马赫数、角度、总压和静压的偏差分别低于0.40%、0.4°、0.06%、0.60%,且相交曲线法的数据处理精度优于样条插值法和最小二乘法。由图10可知,对于非标定数据,各方法处理得到的马赫数、角度、总压和静压的偏差分别低于1.50%、0.2°、0.15%、1.50%,且相交曲线法的数据处理精度与样条插值法和最小二乘法的基本一致。
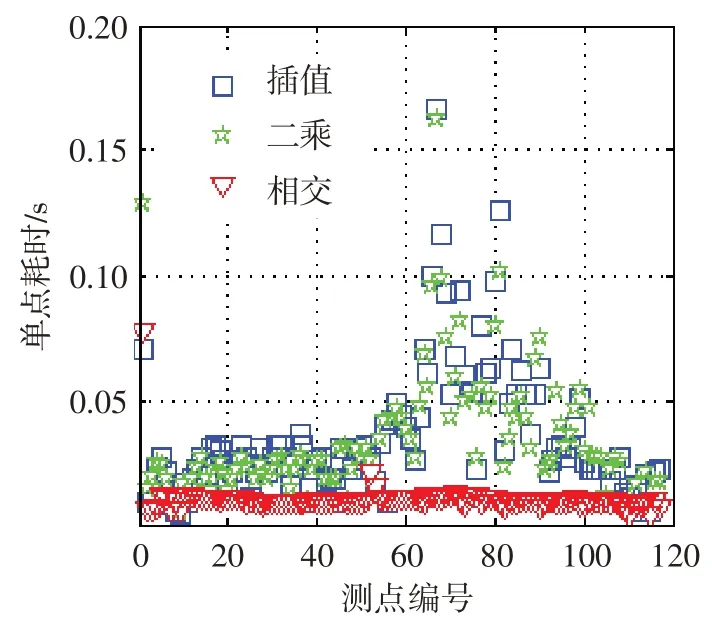
图7 标定点耗时Fig.7 The time of calibratded points
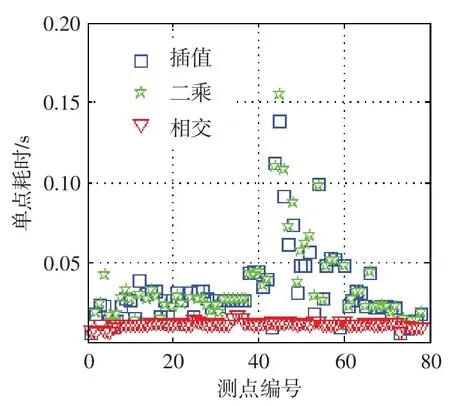
图8 非标定点耗时Fig.8 The time of un-calibrated points
对标定点和非标定点的数据处理精度和效率进行平均处理,获取各方法平均偏差、平均耗时和平均迭代次数,结果见表1。由表可知,各方法均满足工程使用要求;相交曲线法的数据处理精度与样条插值法和最小二乘法的相当,但其迭代次数大幅下降,数据处理效率提高了一倍以上。
6 应用
为进一步评测相交曲线法、样条插值法和最小二乘法在实际应用中的数据处理性能,选择VKI 叶栅[10]进口等熵马赫数为0.900 时的出口流场数据进行处理。图11~图13 为三种方法数据处理结果和效率的对比。相比于样条插值法和最小二乘法,利用相交曲线法进行数据处理时,各测点单点迭代次数均下降至1,单点耗时大幅下降,处理效率提高了一倍以上;三种方法处理得到的出口流场参数分布一致性好,相交曲线法的有效性得到验证。
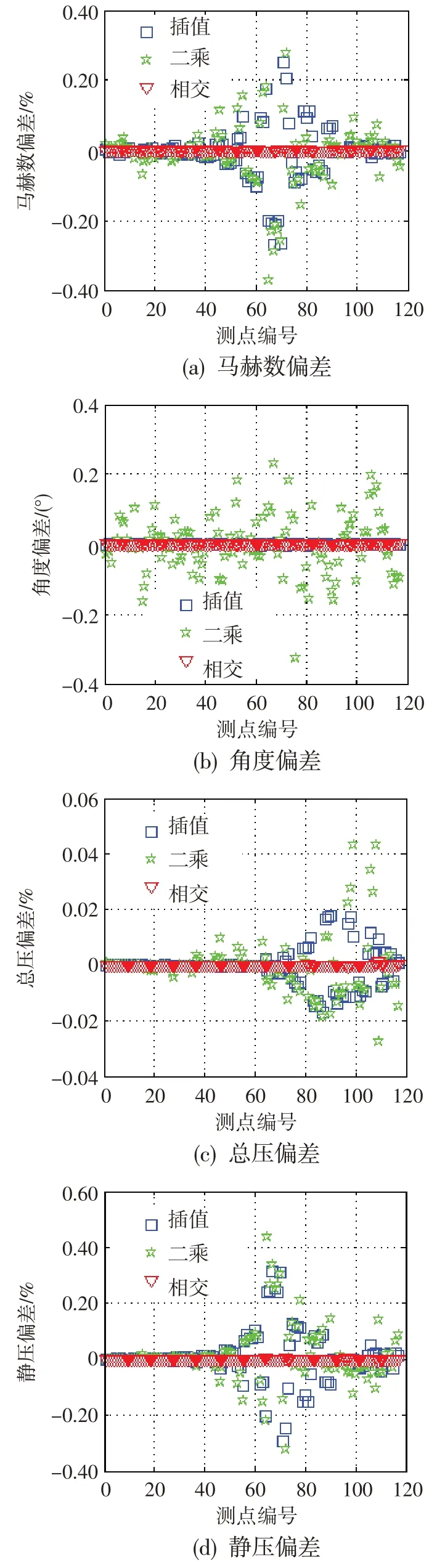
图9 标定点偏差Fig.9 The error of calibratded points
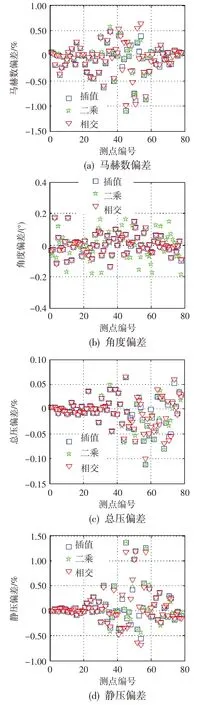
图10 非标定点偏差Fig.10 The time of un-calibrated points
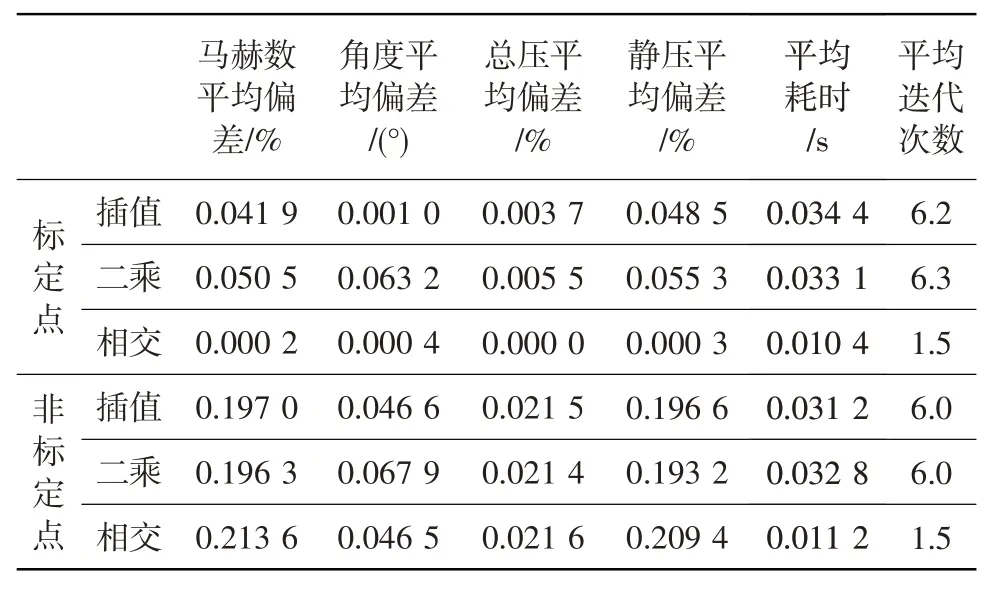
表1 平均精度与效率Table 1 Mean accuracy and efficiency
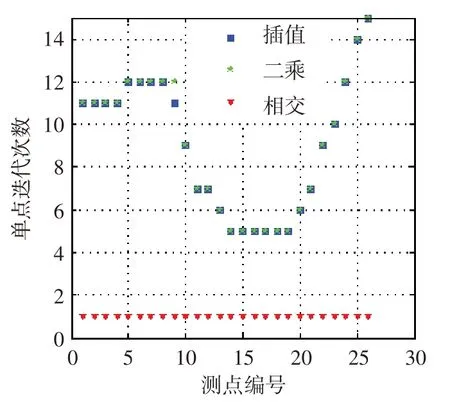
图11 迭代次数Fig.11 Number of iteration
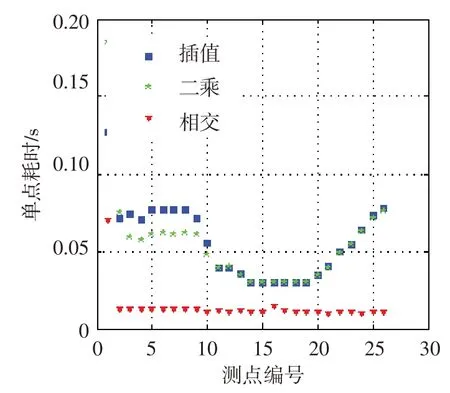
图12 单点耗时Fig.12 The time of a point
7 结论
对三孔压力探针的数据处理方法进行了深入研究,提出一种新的三孔探针数据处理方法——相交曲线法,并与样条插值法和最小二乘法进行了对比,得出以下结论:
(1)相交曲线法实现简单,方法可行;
(2)相对于样条插值法和最小二乘法,相交曲线法的数据处理精度相当,但数据处理效率提高了一倍以上,具有较高的实用价值;
(3)相交曲线法可推广至其他类似结构多孔探针(如五孔探针、七孔探针等)数据处理应用。
