通过调控激光波形获得波长可调的单阶谐波
2020-01-16冯立强
冯立强
(辽宁工业大学 理学院,锦州 121001)
引 言
当强激光场与原子、分子相互作用时会发生许多非线性光学现象。其中,高次谐波作为探测原子、分子中电子超快动力学现象的工具及获得单个阿秒光源的方法被广泛研究近30年[1-3]。
目前,原子、分子辐射高次谐波的过程可由1993年CORKUM提出的半经典“电离-加速-回碰”模型[4]以及1994年 LEWENSTEIN等人[5]改进的量子理论模型来解释。具体来说:电子首先在激光驱动下由隧道电离进入连续态;其次,自由电子在后续激光驱动下加速并获得能量;随后,在激光反向驱动下,电子有几率与原母核发生碰撞,进而辐射出光子能量为基频场整数倍的高阶谐波。基于三步模型[4],人们提出了许多方案来获得持续时间在阿秒量级的单个脉冲。例如:少周期场方案[6];双色或三组合场方案[7-8];啁啾调制方案[9-10];极化门方案[11-12];中红外场方案[13-14];共振增强电离机制[15-16]以及非均匀场调控方案[17-18]。
高次谐波光谱除了可以获得单个阿秒脉冲之外,其另一个非常重要的应用是可以获得能量固定的单阶谐波光源。这一特点对于获得自由电子激光器的种子光源是非常有帮助的。鉴于这一原因,研究人员通过调控激光波形来实现谐波相位匹配,进而获得单阶谐波的选择增强[19-21]。但是,在激光波形的调控中,多数研究都是采用多色场实现的。实验上调控多色场是非常复杂的。而且单阶谐波的增强只在8倍以下。因此,本文中的理论提出一种双色场啁啾场调控方案,并且获得了一种特殊的W波形结构。在该W波形结构下,谐波辐射会呈现折叠区域。当折叠区域仅为单阶谐波时,该阶谐波会比其它谐波强度有明显增强,进而实现单阶谐波的选择增强。在该方案下,单阶谐波增强在20倍左右。本文中单位a.u.表示原子单位,arb.units表示任意单位。
1 计算方法
外场下He原子的薛定谔方程可描述为[22-24]:
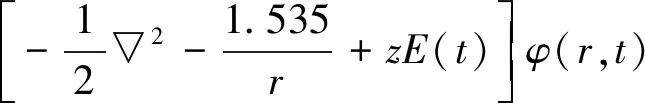
(1)
式中,H(t)为体系哈密顿量,▽为拉普拉斯算符,t表示时间,r为电子坐标,z表示激光偏振方向,φ(r,t)为体系波函数,可由球谐函数来展开(具体方法见参考文献[22]、参考文献[23])。E(t)表示激光场,可描述为:

(2)
式中,Ei,ωi,τi和ci(i=1,2)分别为2束激光场振幅、频率、脉宽和啁啾参量。
高次谐波表示为:

(3)
式中,a(t)=-〈φ(r,t)|[H(t),[H(t),z]|φ(r,t)〉为偶极加速度,ω为谐波阶次。
2 结果与分析
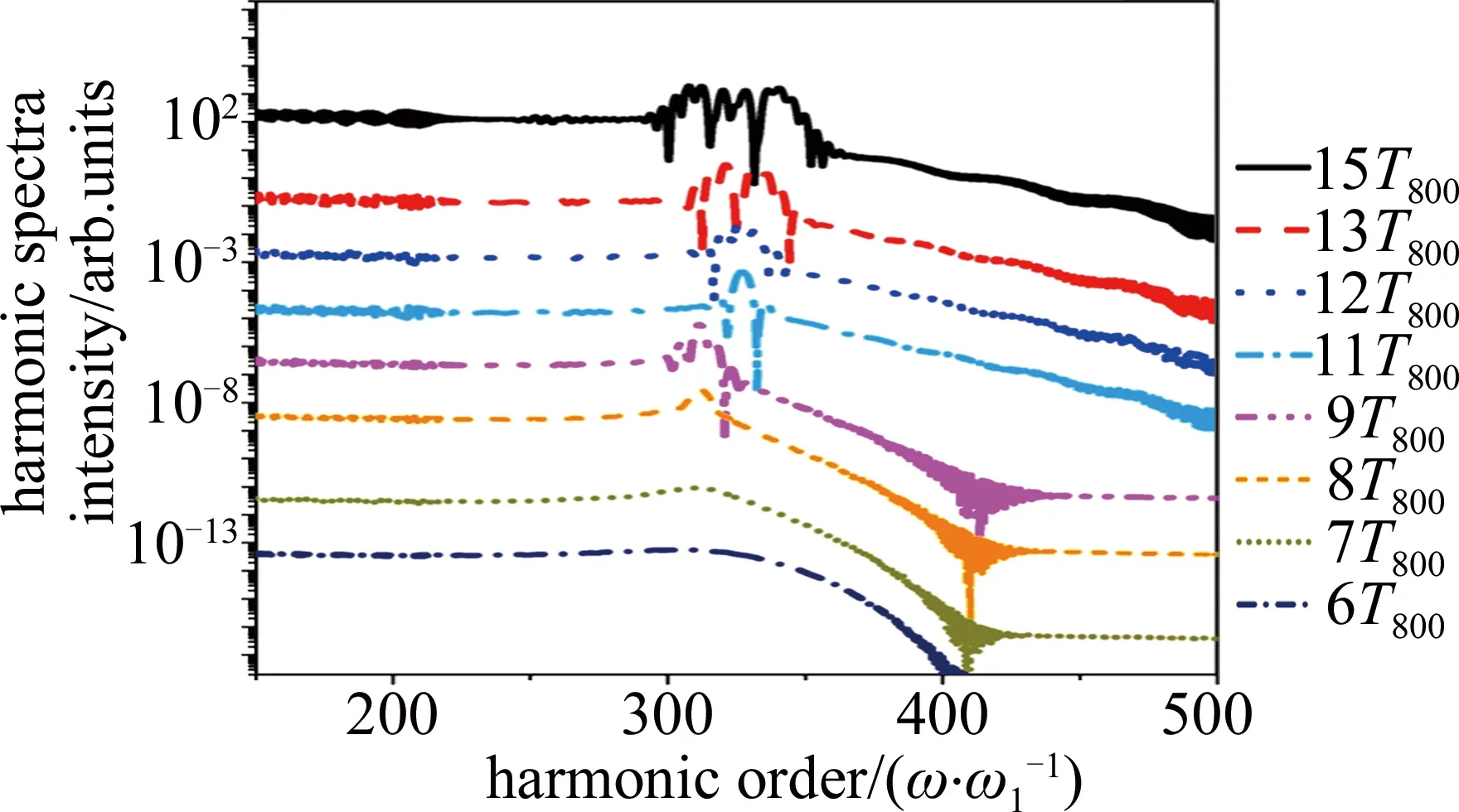
图1为He原子在双色啁啾激光场下辐射高次谐波光谱的谱图。双色场为10T1600以及10T800的组合场。T1600和T800分别表示1600nm激光场和800nm激光场光学周期。激光强度I1=I2=1.0×1014W/cm2。啁啾参量为c1=c2=0以及c1=-6×10-5,c2=0。由图可知,当c1=c2=0时,谐波连续区在55阶~65阶区间有少许增强;当c1=-6×10-5,c2=0时,谐波连续区呈现327阶谐波的单阶增强现象,并且该阶谐波强度比其临近谐波强度增强近20倍。
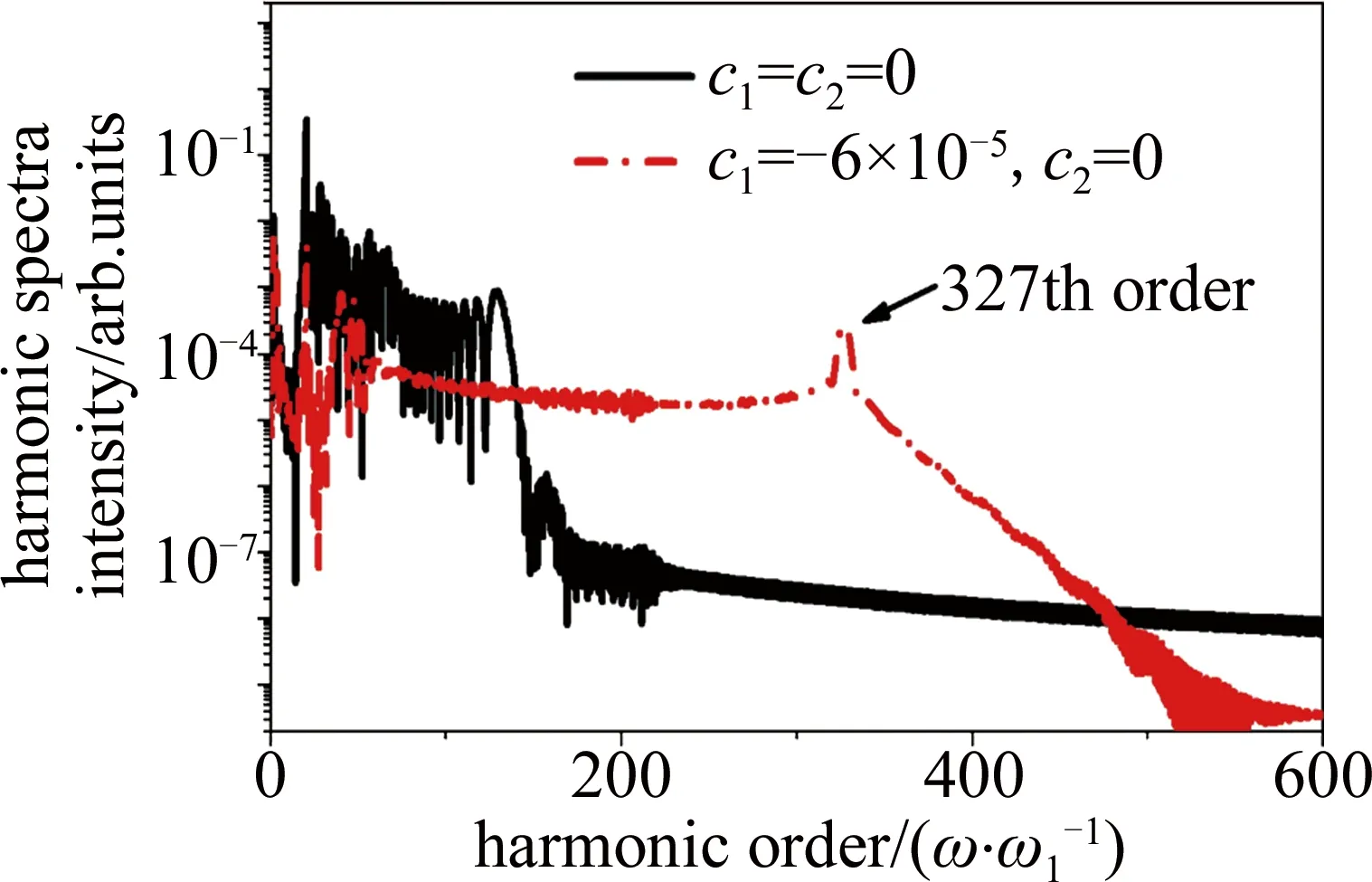
Fig.1 Harmonic spectra from He driven by two-color chirped pulse
图2为He原子在上述双色激光驱动下谐波辐射的时频分析图[25]。为了更好地分析谐波辐射过程,图2中同时给出了He原子在单色10T1600激光下的谐波辐射过程。根据三步模型理论可知,在单色场情况下(见图2a和图2b),电子首先在A点附近发生电离;随后,电子在激光驱动下进行加速;最后在激光反向时,后电离的电子首先在B点与母核发生回碰,进而呈现出谐波辐射能量峰P的短量子路径(左路径);先电离的电子在C点与母核发生回碰,进而形成谐波辐射能量峰P的长量子路径(右路径)。在双色场c1=c2=0情况下(见图2a和2c),电子在A′点电离后,分别在B′和C′点与母核发生回碰,进而辐射出能量P的短、长量子路径。但是在t=0.25T1600~t=0.75T1600之间,激光波形呈现出一个反向的波包,进而形成一个W结构的波形。电子在这一特殊结构下会首先减速然后在加速,这导致谐波辐射能量峰P的短量子路径中呈现了一个折叠区域(如图2c中白色圆圈所示)。这一折叠区域的范围在55阶谐波~65阶谐波,因此这一波段的谐波强度要大于其它波段的谐波强度,这是谐波光谱中这一波段谐波增强的原因。在双色场c1=-6×10-5,c2=0情况下(见图2a和图2d),电子在A″点电离后,其在B″点与母核发生回碰,进而辐射出能量P的短量子路径。观测激光波形可知,W波形依然可以观测到,但是在t=0.25T1600~t=1.25T1600之间,激光波形呈现出两个反向的波包。因此,谐波辐射能量峰P的短量子路径中呈现了两个折叠区域。其中第2个折叠区域仅在327阶谐波附近(如图2d中白色圆圈所示)。这是导致谐波光谱中单独的327阶谐波被选择增强的原因。
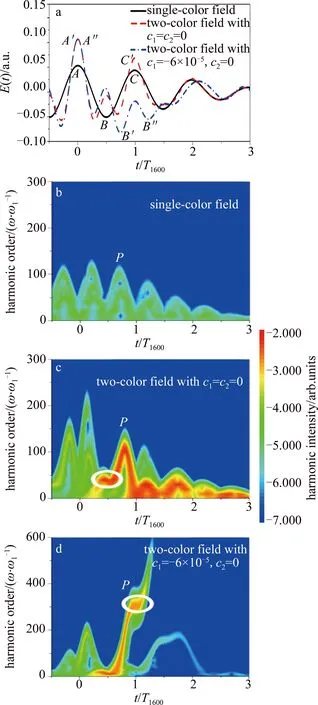
Fig.2 Laser profiles and time-frequency analyses of the harmonics
a—laser profiles b—single-color field c—two-color field withc1=c2=0
d—two-color field withc1=-6×10-5,c2=0
图3中给出了不同啁啾组合下谐波选择增强的效果。其中1600nm激光的啁啾参量固定为c1=-6×10-5。由图3可知,当c2从0变换到8×10-5时,谐波光谱呈现波长可调的单阶谐波增强。具体来说,单阶谐波增强范围在182阶谐波~328阶谐波,如图3a所示。当c2>8×10-5时(例如9×10-5≤c2≤15×10-5),谐波光谱呈现双谐波增强效果,如图3b所示。
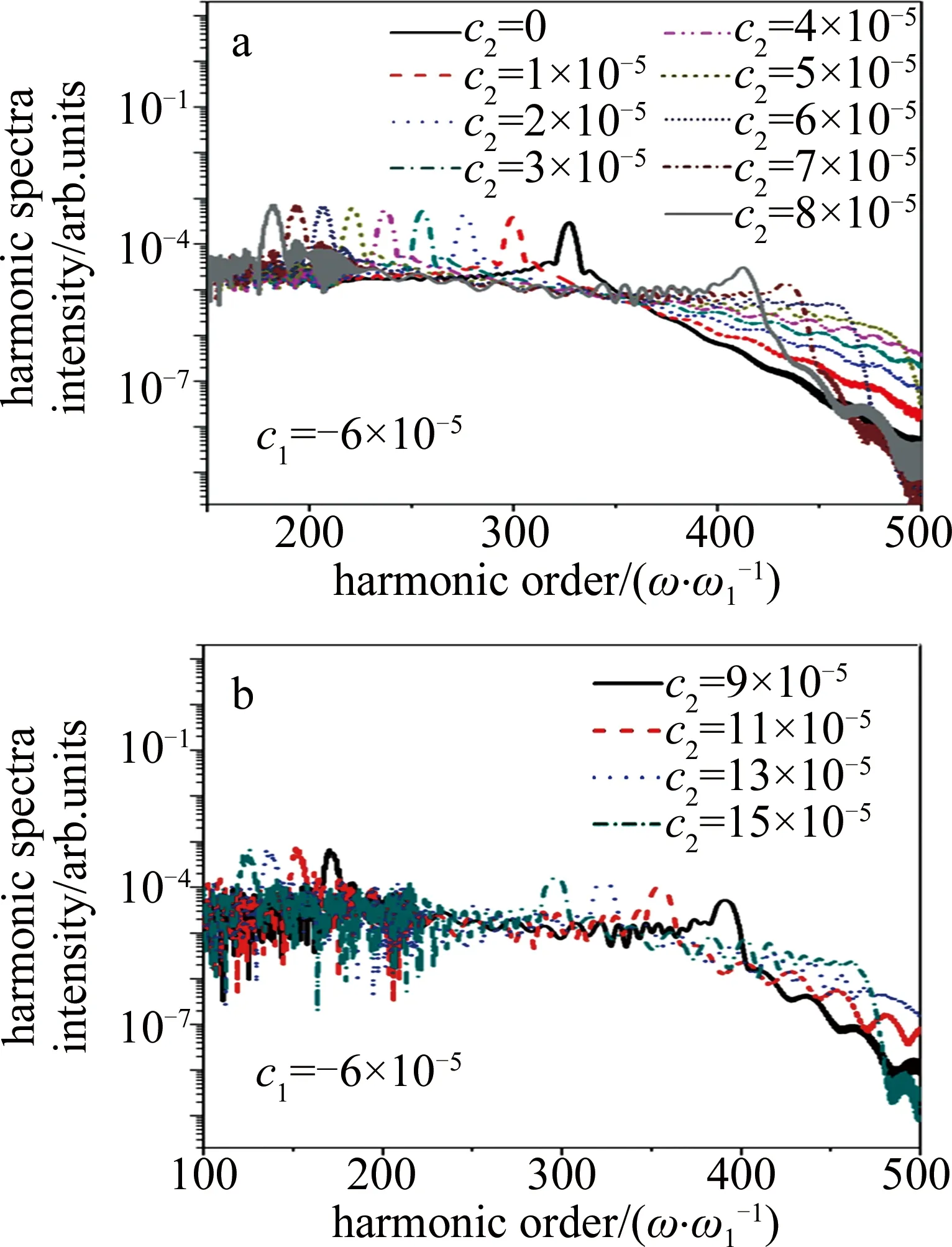
Fig.3 Harmonic spectra driven by two-color chirped pulse
图4是双色啁啾激光驱动下谐波辐射的时频分析图。这里只给出2种条件来说明谐波选择增强的原因,即单阶谐波(c1=-6×10-5,c2=6×10-5)以及双谐波(c1=-6×10-5,c2=11×10-5)增强。对于c1=-6×10-5,c2=6×10-5的情况(见图4a),在t=0.25T1600~t=1.0T1600区间,激光波形呈现2个反向波包。因此,当自由电子在B点与母核回碰时,谐波辐射能量峰P会呈现2个折叠区域。对于第2个折叠区域,其折叠能量仅在207阶谐波附近(见图4a中白色圆圈区域),因此导致谐波辐射光谱上呈现单阶谐波增强。对于c1=-6×10-5,c2=11×10-5的情况(见图4b),在电子电离以及回碰区间内(0.25T1600 Fig.4 Laser profiles and time-frequency analyses of the harmonics 图5中给出了800nm激光脉宽变化对于谐波选择增强的影响。从图中可见,当800nm激光脉宽大于11T800时,虽然部分谐波依然可以被增强,但是很难实现单阶谐波的选择增强;当800nm激光脉宽在8T800~11T800之间时,谐波光谱可以呈现单阶谐波的选择增强;但是当800nm激光脉宽在8T800以下时,单阶谐波的选择增强效果又消失了。 Fig.5 Effect of 800nm pulse duration on the selective enhancement of single-order harmonic order Fig.6 Laser profiles and time-frequency analyses of the harmonics 图6是不同800nm激光脉宽下谐波辐射的时频分析图。根据之前分析可知,谐波的选择增强来自于谐波辐射过程中的折叠区域,而折叠区域又是激光波形中反向波包所导致的。分析图6中的激光波形可知,对于多周期脉宽情况(13T800),由于t=1.25T1600附近的激光振幅很明显,这导致激光波形在t=0.75T1600~t=1.25T1600之间呈现了明显的反向波包。因此,自由电子在该区域的减速和加速会非常明显,进而在谐波辐射能量峰P中形成能量范围较大的折叠区域,如图6a所示。对于激光脉宽为11T800和9T800的情况,t=1.25T1600附近的激光振幅与多周期脉宽相比又明显减小,因此导致谐波辐射过程中的折叠区域范围减小。具体来说,对于11T800和9T800的情况,谐波辐射能量峰折叠范围分别在328阶谐波和312阶谐波附近,如图6b和6c所示,这是导致谐波光谱上单阶谐波选择增强的原因。对于少周期脉宽情况(例如:7T800),t=1.25T1600附近的激光振幅非常弱,这导致t=0.25T1600~t=1.25T1600之间的第2个反向波包几乎消失不见。因此,在谐波辐射能量峰中观察不到折叠区域,如图6d所示。这是导致谐波光谱上单阶谐波增强消失的原因。 本文中提出一种利用双色啁啾场调控激光波形获得单阶谐波增强的理论方案。结果表明,在啁啾激光调节下可以获得了一种特殊的W波形结构。在该W波形结构下,谐波辐射会呈现折叠区域。当折叠区域的覆盖范围仅为单阶谐波时,该阶谐波强度会比其它谐波强度有近20倍的增强。随后通过优化激光波形可以获得单阶谐波增强的范围在182阶谐波~328阶谐波。 本文中提出了一种新的获得单阶谐波甚至双谐波的方法,虽然还未进行实验验证,但是本文中采用的理论方法已经被实验证明其正确性和准确性[21-22]。因此,该研究对激光光源的发展有一定帮助。 非常感谢中国科学院大连化学物理研究所韩克利研究员所提供的计算资源。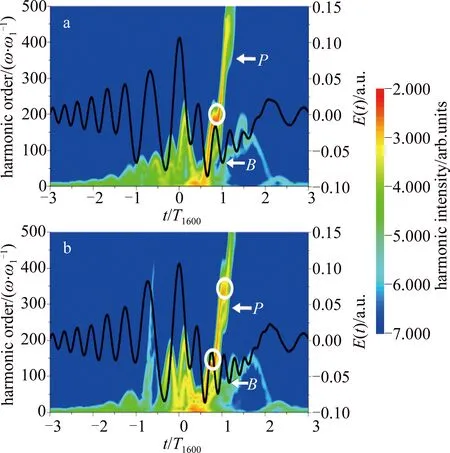

3 结 论
