基于模糊聚类的模糊软集群决策逆判问题

李 雪, 陈 岩

(1.沈阳工业大学 理学院, 辽宁 沈阳 110870； 2.沈阳工业大学 管理学院， 辽宁 沈阳 110870)

传统数学工具如概率论、区间数学可以解决含有不确定性的问题,但Zadhe[1]于1965年提出的模糊集理论迅速成为解决不确定性问题的重要工具,在运用模糊集理论解决实际问题时,由于问题的性质更依赖于隶属函数的设定,所以隶属函数的确定变得尤其重要.为了处理不确定性问题,Molodtsov[2]于1999年提出了软集合理论的概念,它作为一种解决不确定性问题的数学工具,借助二元信息对目标进行分类,可以不受目标属性集的限制,且没有产生隶属函数.Maji[3]等研究了关于软集合理论的运算,如交、并、补、与和或运算等,并将软集合理论应用于多个方向,此后软集合理论的性质及应用得到国内外研究者的重视.Feng等研究了基于软集合理论的群决策应用问题[4-5].Maji等通过嵌入模糊集理论的思想,将模糊集与软集相结合,得到了模糊软集合理论,并扩展了模糊软集合在群决策中的应用[6-7].Majumdar等进一步扩展了模糊软集合理论，提出了广义模糊软集[8]，Wang等提出了犹豫模糊软集及其在多属性群决策问题中的应用[9].

在实际的群决策问题中,专家的判断会受到个人背景、偏好以及主观倾向等因素的影响,给出的决策矩阵或判断矩阵中的元素往往具有不确定性,导致群决策难以有效地进行.只有专家群体判断达成共识,群决策的结果才有意义,因此如何快速地寻找出大规模群体中的非合作专家成为一致性群决策的研究热点.Palomare[10]等提出了一种适用于大规模决策的决策模型,运用模糊聚类方法来检测和管理个体和群体的非合作行为.随后,Quesada[11]等认为通过减少重要性来管理非合作行为的专家意见稍有欠缺,从而提出了一种基于模糊集合和语言计算的新方法用以识别和管理并改进非合作专家的行为和意见.将专家权重与一致性动态过程相结合并研究了其在非合作群决策过程中的应用[12].Xu等对具有非合作行为的多属性大规模群决策问题给出了决策的共识模型[13].所谓逆判问题,就是在大规模群决策中,为进一步提高群决策质量,对参与决策的专家评判水平进行评判,找出非合作专家.刘万里[14]首先对基于互反判断矩阵的群决策逆判问题给出了一种统计分析方法.陈岩等[15-17]针对基于语言信息判断矩阵的群决策问题提出了基于方差的假设检验方法，针对互补判断矩阵通过等转换为互反判断矩阵，提出一种改进的统计分析方法，并将区间数信息转化为互反判断矩阵，提出了基于区间数信息的群决策逆判方法.陈侠等[18]利用相对偏差改进了基于互补判断矩阵的逆判问题分析方法.巩在武等[19]借助相关度给出了直觉模糊判断矩阵的群决策逆判问题分析方法.夏梅梅等[20]针对区间直觉模糊判断矩阵的群决策逆判问题给出了基于相似度的分析方法.

本文运用模糊聚类算法来处理模糊软集群决策逆判问题,模糊聚类算法能快速将专家群体分类,提高决策质量.模糊聚类算法较传统K-means算法比较,有其独特的优势,传统K-means算法进行聚类时需要考虑初始类簇中心点的选择,还需要考虑分为几类,而本文则使用模糊聚类算法进行动态分析,从而快速聚类.首先定义模糊软集的决策矩阵,然后给出决策矩阵的规范化形式,通过计算两个矩阵之间的相似性得到一个模糊相似矩阵,进一步通过模糊聚类的方法对专家进行分类,即从每一个类别的专家群体中选择一位专家,通过构造的互反判断矩阵，对挑选出的专家进行一致性检验,从而找出非合作专家群体,完成对专家水平的评判,最后通过一个例子说明该方法的有效性.

1 基本概念

定义1[2]设U为初始论域,P(U)为U的幂集,E是所有参数集的集合且A⊆E.那么论域U上的一个软集通过一个函数的映射来定义：

fA:E→P(U),若x∉A,则fA(x)=∅.

其中：fA是软集FA的近似函数,fA的值是一个集合,称为软集的x元素集.值得注意的是,fA是任意的,可以是空的,也可以是非空的集合.因此论域U上的一个软集可用序对的集合表示为

定义2[1]设U为非空集合,U中的一个模糊集合通过它的隶属函数μx:U→[0,1]来描述,其中μX(x)为模糊集X中x元素的隶属度.则X用集合来表示为

定义3[6]设U为初始论域,E是所有参数集的集合且A⊆E,IU表示U上所有模糊子集的幂集.则(F,E)为论域U上的一个模糊软集,其中F为一个映射：F:A→IU.

定义4[6]设(F,A)和(G,B)为论域U上的两个模糊软集,若满足(i)A⊂B,(ii)∀ε∈A,F(ε)是G(ε)的模糊子集,则称(F,A)是(G,B)的模糊软子集.

定义5[6]设(F,A)补集(F,A)c,定义(F,A)c=(Fc,┑A),其中Fc:┑A→IU是一个映射且对于∀α∈┑A,Fc(α)是F(┑α)的模糊补.

定义6[21]设(F,E)为论域U上的一个模糊软集,则(F,E)的模糊关系定义为

其中隶属函数μRA记为μRA:U×E→[0,1].若U={u1,u2,…,um},E={e1,e2,…,en}，且A⊆E,则RA可用表1表示.

表1 模糊软集(F,E)的关系表示Table 1 Relational representation of fuzzy soft sets(F,E)

假设aij=χRA(ui,ej),可以定义一个矩阵

叫做模糊软集(F,E)在U上的模糊软矩阵.

根据这个定义,一个模糊软集(F,E)可以由模糊软矩阵[aij]m×n唯一表示.这意味着模糊软集(F,E)在形式上和它的模糊软矩阵[aij]m×n等价.因此,可以用模糊软矩阵确定任何模糊软集并且这两个概念可以相互交换使用.所有在论域U上的m×n阶模糊软矩阵的集合可以用FSMm×n来表示.

定义7[6]如果(F,A)和(G,B)是两个模糊软集,则两者的并集为(H,C),其中：C=A∪B,∀e∈C,有

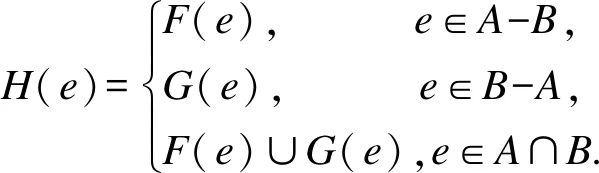
定义8[6]如果(F,A)和(G,B)是两个模糊软集,则两者的交集为(H,C),其中:C=A∩B,∀e∈C,H(e)=F(e)或G(e).

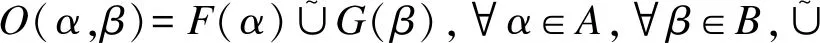
2 相似性度量

在很多文献中,已经研究了两个模糊软集之间的相似性度量,有基于距离的相似性度量,还有基于匹配函数的相似性度量,还有一些基于集合理论的相似性度量.这里主要介绍集合理论的相似性度量[22].

定义11F(ei)和F(ei)的ei近似值的相似性为

(1)

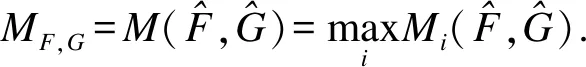
性质1 (i)M(F,G)=M(G,F); (ii) 0≤M(F,G)≤1; (iii)S(F,F)=1.

那么M1=0.68,M2=0.59,M3=0.39,M4=0.72,因此,MF,G=max{M1,M2,M3,M4}=0.72.

定义12 设有p(p≥2)位专家,则模糊相似矩阵为C=[cij]n×n,其中：

3 模糊软矩阵的互反导出矩阵与一致性分析

在决策过程中,研究判断矩阵的一致性尤其重要,只有判断矩阵具有一致性或弱一致性,决策结果才有意义,否则决策结果会产生矛盾.通过对同一个专家基于权重参数进行两两方案的比较,得到两个方案的比较值来构造互反导出矩阵.

定义13 设D=[di*j*]m×m为模糊软矩阵A=[aij]m×n的互反导出矩阵,则有

D=[di*j*]m×m=

(2)

其中：1≤i*≤m,1≤j*≤m,wj为模糊软集中参数的初始权重,由专家根据参数的重要程度给出.当di*j*=1时,表示方案i*与方案j*无差别;若di*j*>1,则表示方案i*优于方案j*;若di*j*<1,则表示方案j*优于方案i*.

性质2[16]设D=[di*j*]m×m为模糊软矩阵的互反导出矩阵,则

(1) 对所有的i*=1,2,…,m;di*i*=1.

(2) 对所有的i*,j*=1,2,…,m；di*j*×dj*i*=1.

定义14 对于互反判断矩阵D=[di*j*]m×m,若满足di*k*×dk*j*=di*j*,则称D为完全一致性矩阵.

4 基于模糊聚类算法对专家进行聚类分析

在大规模群决策过程中,运用模糊聚类的方法将专家根据专家群体之间的相似性进行分类.

定义15[23]设R∈F(X×X),如果对任意λ∈[0,1]及任意x,y,z∈X满足:R(x,y)≥λ,R(y,z)≥λ⟹R(x,z)≥λ,则称R是传递的.

定义16[23]若R是X上的自反、对称、传递的模糊关系,则称R是X上的模糊等价关系.

定义17[24]设R∈F(X×X),若R1∈F(X×X)是传递的且满足：(i)R⊆R1;(ii)若S是X上的模糊传递关系且R⊆S,必有R1⊆S,则称R1为R的传递闭包,记为t(R).

根据上述定义,模糊关系R的传递闭包是包含R的最小传递关系.

模糊聚类算法对专家进行逆判的具体步骤如下:

步骤2 运用定义12,求模糊相似矩阵C=[cij]p×p.

步骤3 求传递闭包,求C2,C4,C8,…,得到模糊相似等价矩阵t(C),选取适当的置信水平值λ∈[0,1],按λ截矩t(C)λ,进行动态聚类.

步骤4 从所期望的每个类别中挑选出一位专家,将其模糊软矩阵转换为互反判断矩阵D=[di*j*]m×m,随后进行一致性检验,挑选出非合作专家,并对专家水平进行评判.

5 算 例

步骤2 计算模糊相似性矩阵C=[cij]p×p如下:

步骤3 得到模糊相似等价矩阵t(C)如下:

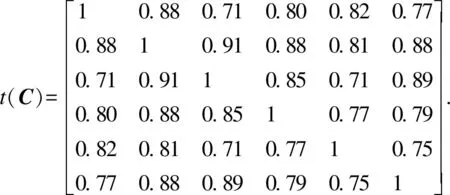
把t(C)中的元素从小到大的顺序编排如下:

0.71<0.75<0.77<0.79<0.80<0.81<0.82<0.85<0.88<0.89<0.91<1.

依次取λ等于上述值,由于算例中有6位专家,应将专家分为2类或3类较为合理,所以当λ=0.75时有

这时专家群体被分为3类:{x1,x5},{x2,x4,x6}{x3},即当置信域取区间(0.71,0.75]时,专家分类较为合理,即

L1={x1,x5},L2={x2,x4,x6},L3={x3}.

步骤4 从L1、L2、L3中分别挑选出一位专家,在L1中选择专家5,在L2中选择专家4,在L3中选择专家3进行一致性检验,结果如下:

专家5的互反导出矩阵为

专家4的互反导出矩阵为

专家3的互反导出矩阵为

计算专家5、4、3的一致性比率：CR5=0.115 8,CR4=0.032 4,CR3=0.09.由于CR5>0.1,可认为专家5具有较差的一致性,专家5所在的类别L1中的专家的一致性较差,故专家1、5的评判水平较差;由于CR4≤0.1,可认为专家4具有较好的一致性,专家4所在的类别L2中的专家的一致性较好,故专家2、4、6的评判水平较好;由于CR3≈0.1,可认为专家3的一致性较好却差于专家4,专家3所在的类别L3中的专家的一致性一般,故专家3的评判水平一般.

6 算法复杂度对比分析

在大规模群决策逆判问题中,假设有N位专家针对n个方案给出导出矩阵为Q=(qij)n×n,分别运用基于偏差度量的逆判分析和基于聚类分析的逆判分析两种方法对专家一致性水平进行排序.

6.1 基于偏差度量的逆判分析

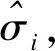
(1) 利用和积法求Q=(qij)n×n最大特征值所对应的特征向量w=(w1,w2,…,wn)T，计算每位专家权重的wi的运算次数为n2+3n+1次,则N位专家的运算次数为N·(n2+3n+1).

(2) 计算每个判断矩阵的偏差矩阵δij,其中每个判断矩阵的运算次数为n2+2次,则N位专家的运算次数为N·(n2+2).

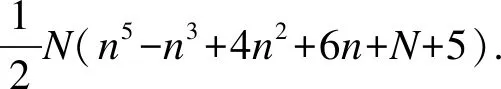
6.2 基于聚类分析的逆判分析

首先将模糊软矩阵规范化,求其模糊相似矩阵,利用模糊聚类的方法进行动态聚类,由于每个类别中的专家具有相似性,只需要在每个类别中挑选出一位专家,将其模糊软矩阵转化为互反判断矩阵,计算其一致性,最后进行排序.

(1) 将模糊软矩阵最大规范化,每位专家的运算次数为n2,N位专家的运算次数N·n2.

6.3 算法小结

两种算法的计算复杂度均与专家的个数和矩阵的阶数(即决策矩阵中方案的个数)有关,第一种算法的复杂度为o(N·n5+N2),而第二种算法的复杂度为o(N·n2+N2·n),显然在大规模群决策问题中,使用聚类算法对专家群体进行逆判问题分析具有较高的效率, 能够大幅度减少总体搜索的计算量.

7 结 论

运用模糊聚类算法解决模糊软集群决策逆判问题,提出一种基于模糊软集的群决策逆判方法.运用模糊聚类算法对专家群体进行动态聚类,可以快速找出非合作专家,从而对专家评判水平进行评判.通过对算法的复杂度分析,说明模糊聚类算法减少了计算的复杂性,有助于提高大规模群体决策的质量与效率.