基于一致性局部调整算法和DEA的语言偏好决策模型
2020-01-16金飞飞倪志伟陈华友朱旭辉武文颖
金飞飞,倪志伟,陈华友,朱旭辉,武文颖
(1.安徽大学商学院,安徽 合肥 230601;2.合肥工业大学管理学院,安徽 合肥 230009;3.过程优化与智能决策教育部重点实验室,安徽 合肥 230009;4.安徽大学数学科学学院,安徽 合肥 230601)
1 引言
决策作为现实生活中最常用的一种活动,已经广泛应用于各个领域[1]。由于实际决策问题具有模糊性、不确定性等特征,再加上人类思维存在局限性,使得许多决策信息不能简单地运用精确值进行描述[2]。对此,Zadeh提出模糊集理论[3],其运用隶属度来描述集合中元素的模糊性。在决策过程中,专家们通常将一组备选方案进行两两比较后给出相应的评价信息,从而构造包含决策信息的偏好关系。模糊偏好关系[4-5]和乘性偏好关系[6-7]是两种最为常用的偏好关系形式。然而上述这些偏好关系的一个共同点就是评价信息均是用数字进行表达,而语言信息能够贴近于人类的认知,所以运用语言变量表达决策者评估信息更为合理和直观。因此,Zadeh[8]于1975年提出了模糊语言方法。随后,专家们引入语言偏好关系[9-11]的概念用于对决策信息进行更为直观和定性的表达。
由于运用缺乏一致性的偏好关系进行计算容易导致出现不合理甚至错误的决策结果[12]。因此,一致性分析和排序权重的确定是研究偏好关系的两个主要课题。为了探究偏好关系的基本性质和特征,Xu Zeshui[4]对现有偏好关系进行了总结研究,并提出了几类新的偏好关系。Herrera-Viedma等[13]详细分析了模糊偏好关系一致性的特征性质,然后设计了一种基于原始数据构建具有一致性的模糊偏好关系方法。针对评价信息为直觉模糊数的群决策问题,Jin Feifei等[14]首先定义了直觉模糊偏好关系的有序一致性和乘性一致性概念,设计了一种乘性一致直觉模糊偏好关系与直觉模糊权重向量进行相互转化的方法,进而建立了两种群决策方法用于确定方案的排序权重向量。Xu Zeshui和Liao Huchang[15]针对直觉模糊偏好关系的概念、一致性、相容性以及排序方法等进行了全
面的总结和分析。在犹豫模糊信息环境下,Zhang Zhiming等[16]构建了一个包含有一致性迭代改进过程、相容性实现过程以及方案选择过程的决策支持模型。针对决策者给定的犹豫模糊偏好关系,Zhu Bin等[17]提出一种基于最优化模型的乘性一致性迭代调整算法,使得调整后的犹豫模糊偏好关系具有满意一致性。Zhang Zhiming和Wu Chong[18]基于犹豫乘性偏好关系的一致性计算区间排序权重向量,进而对方案进行排序。Wu[19]提出了一种整合DEA和模糊偏好关系的模型得到方案排序,并构造一种交叉评估模型。Lin Yang和Wang Yingming[20]将DEA引入到犹豫乘性偏好关系中,设计了两种优先排序方法。
近年来,对语言偏好关系及其拓展形式的一致性和排序权重确定方法的研究也越来越受到学者们的专注[21-22]。针对不一致的语言偏好关系,Jin Feifei等[23]研究了基于自迭代模型和基于最优化模型的加行一致性调整算法对原始语言偏好关系进行调整,从而使得调整后的语言偏好关系具有满意一致性。Dong Yucheng等[24]提出一种基于最优化模型的算法用于改进非对称语言偏好关系一致性水平,从而使得原始语言偏好关系中的决策信息能够得到尽可能多的保留。虽然对语言偏好关系的研究越来越深入,但是现有的很多语言偏好关系模型方法存在着一些不足。借鉴于模糊偏好关系的乘性一致性定义,Jin Feifei等[25]提出了语言偏好关系乘性一致性的概念,其揭示了乘性一致语言偏好关系与排序权重向量之间的内在联系,然后以最小化偏差为准则建立最优化模型,构建具有收敛性的语言群决策迭代算法计算出排序权重向量,并通过对供应链中供应商的选择算例验证了提出的群决策模型是科学有效的。Zhu Bin和Xu Zeshui[26]在首次定义犹豫模糊语言偏好关系的概念之后,提出了一系列的犹豫模糊语言偏好关系一致性度量方法,并分别建立了基于最优化模型和基于反馈机制的收敛迭代算法用于提高犹豫模糊语言偏好关系的一致性。针对非加性一致性的犹豫模糊语言偏好关系,Wu Zhibin和Xu Jiuping[27]定义了新的一致性指数公式,并基于犹豫模糊语言偏好关系对应的二元语言偏好关系和加行一致语言偏好关系,建立了一种新的一致性迭代调整算法,该算法虽然能够对非一致性程度最大的元素进行调整,但是调整的幅度太大,容易丢失过多的原始决策信息。对于非乘性一致性的犹豫模糊语言偏好关系,Zhang Zhiming和Wu Chong[28]首先将其转化为标准的犹豫模糊语言偏好关系,然后设计一种具有收敛性的自动迭代算法对标准的犹豫模糊语言偏好关系进行调整,使得修复后的犹豫模糊语言偏好关系达到一致性阈值。Pei Lidan等[29]基于加性一致直觉模糊语言偏好关系与直觉模糊权重向量之间的关系,建立了一种基于最优化模型的自迭代决策方法,该方法不仅能够提高直觉模糊语言偏好关系加性一致性,还可以帮助决策者获得合理可靠的决策结果。Xu Zeshui[30]直接运用提出的语言算术平均算子对语言偏好关系进行信息融合的计算。然而,运用非一致性的语言偏好关系进行计算容易出现非一致的决策结果。因此,运用Xu Zeshui[30]中的方法计算得到的决策结果不一定合理可靠。针对非一致性的语言偏好关系,Dong Yucheng等[31]建立了一种一致性改进算法用以提升原始语言偏好关系的一致性水平。但是在调整的过程中,通过该算法生成的具有加行一致性的语言偏好关系相较于原始语言偏好关系有了较多元素和较大幅度的改变,从而造成原始决策信息的大量丢失,迭代过程中生成新的语言偏好关系的决策过程随机性太强。针对不具有满意加性一致性的不确定二元语言偏好关系,Zhang Zhen和Guo Chonghui[32]首先提出了一种加行一致不确定二元语言偏好关系的构建方法,然后设计了新的加性一致性迭代算法对原始的不确定二元语言偏好关系进行提升。然而,运用Zhang Zhen和Guo Chonghui[32]的调整算法每进行一次迭代,都需要对原始的不确定二元语言偏好关系的大部分信息进行调整,同时构建得到的加行一致不确定二元语言偏好关系中的元素可能不在规定的语言术语集领域之内。(具体可见案例分析部分)。
针对上述问题,本文提出了构造乘性一致语言偏好关系的方法,为了尽可能保留原始决策信息,引入局部调整策略,设计了一种具有收敛性的乘性一致性改进算法,使得改进后的语言偏好关系具有满意乘性一致性。随后,基于DEA模型建立了最优化模型,进而确定方案的排序权重向量。最后,构建一个基于一致性局部调整策略和DEA方法的语言决策模型,从而得到合理可靠的决策结果。
2 基本概念
假设S={s0,s1,…,s2τ}是一个元素个数为奇数且全排序的语言术语集[8],其中si表示语言变量,2τ+1表示语言术语集S的基数。这里τ是一个正整数,那么2τ为一个偶数,并且2τ的取值必须满足以下条件:(i)能够避免语言术语集S中的元素个数过多而造成对决策专家施加无用的精度;(ii)语言术语集S中的元素必须足够丰富,以便允许在有限数量的评价等级中辨别或区分每个评价对象的优劣性能。因此,通常情况下,语言术语集S的基数2τ+1取值7或9,通常不超过11[33]。语言集S需要具有以下两个特征:(1)若α≥β,则sα≥sβ。因此,存在最大最小算子;(2)存在逆算子:neg(sα) =s2τ-α,特别的neg(sτ)=sτ。
例1 为了描述一座房屋外观,决策者可利用语言集S={s0:极差,s1:很差,s2:差,s3:稍差,s4:一般,s5:稍好,s6:好,s7:好,s8:极好}中的语言变量进行评价。


定义1[23]:假设X={x1,x2,…,xn}是一个方案集,定义在X上的判断矩阵A=(aij)n×n是一个语言偏好关系,其中aij∈S且
aij+aji=s2τ,aii=sτ,∀i,j∈N
(1)
这里aij表示方案xi相对于xj的语言偏好度。特别的,当aij=sτ时,表示xi与xj间无差异;当aij>sτ时,表示xi优于xj;aij越大表示xi相对于xj越优;当aij=s2τ时,表示xi完全优于xj。
定义2[4]令A=(aij)n×n是定义在X上的语言偏好关系,那么A=(aij)n×n具有乘性一致性,如果其满足如下乘性传递性:
I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i (2) 定义3[12]:令A=(aij)n×n是定义在X上的语言偏好关系,那么A=(aij)n×n具有乘性一致性,如果存在一个排序权重向量w=(w1,w2,…,wn)Τ,使得: (3) 本节主要研究如何构造乘性一致语言偏好关系,然后设计一种基于局部调整策略的一致性改进算法,并证明算法的收敛性。 定理1假设A=(aij)n×n是定义在X上的语言偏好关系,其中aij∈S,那么下面命题等价: (i)A具有乘性一致性。 证明:(i)⟹(ii) 因为命题(ii)可以转化为:当 I(aij) (4) 因此只需证明当A具有乘性一致性时,公式(4)成立即可。 因为i,j∈N,i I(ai,i+k) (5) 接下来将运用数学归纳法证明公式(5)成立。当k=1时,则显然有: 假设当k=l时公式(5)成立,则有: I(ai,i+k) (6) 当k=l+1时。由于A具有乘性一致性,则有 I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i 于是对于i I(ai,i+l+1)I(ai+l+1,i+l)I(ai+l,i) =I(ai,i+l)I(ai+l,i+l+1)I(ai+l+1,i) 所以I(ai,i+l+1)·(2τ-I(ai+l,i+l+1))·(2τ-I(ai,i+l))=I(ai,i+l)·I(ai+l,i+l+1)·(2τ-I(ai,i+l+1)),从而有: I(ai,i+l+1)={2τ·I(ai,i+l)·I(ai+l,i+l+1)}/I(ai,i+l)·I(ai+l,i+l+1)+(2τ-I(ai,i+l))(2τ-I(ai+l,i+l+1)) (7) 于是证明了当k=l+1时,公式(5)成立。 (ii)⟹(i) 根据上述证明过程可知,命题(ii)可转化为公式(4)。令i I(aik) (8) I(akj) (9) I(aij)I(ajk)I(aki)=I(aij)·(2τ-I(akj))·(2τ-I(aik)) (10) I(aik)I(akj)I(aji)=I(aik)·I(akj)·(2τ-I(aij)) (11) 因此I(aij)I(ajk)I(aki)=I(aik)I(akj)I(aji),i 依据定理1,容易得到如下结论成立,即: 定理2假设A=(aij)n×n是定义在X上的语言偏好关系,其中aij∈S,令 (12) 根据定理2可以得到如下推论。 (13) 根据公式(13)显然有CI(A)∈[0,1]。CI(A)的值越小表示A的一致性程度越高。如果CI(A)=0,则表示A具有完全乘性一致性。 对于非满意乘性一致性的语言偏好关系A=(aij)n×n,接下来将运用局部调整策略设计一种一致性改进算法,使得改进后的语言偏好关系不仅具有满意乘性一致性,而且使得原始的语言偏好关系A=(aij)n×n中元素变化程度最小,从而最大程度保留原始的决策信息。 基于局部调整策略的一致性改进算法设计如下: 算法 I (14) (15) 令t=t+1,返回步骤2。 步骤7结束。 接下来将证明上述迭代算法是收敛的。 (16) CI(A(t+1)) (17) 综上,定理3结论成立。 本节首先提出一种基于DEA的权重确定方法,探究方案的相对效率得分与排序权重向量之间的关系,然后构建新的语言决策模型,最终得到合理可靠的决策结果。 在决策问题中令X={x1,x2,…,xn}是一个有限方案集,A=(aij)n×n是定义在X上的语言偏好关系。基于DEA理论,在决策过程中可将每个方案xi看成是一个独立的决策单元DUMi。通常情况下,如果备选方案xp优于xi,即xp≻xi,那么在语言偏好关系A=(aij)n×n中的信息就表现为apk≥aik,k∈N,即I(apk)≥I(aik),k∈N,这符合DEA模型产出变量的特征。因此,A=(aij)n×n的每一列可以看成是一类产出。另一方面,由于DEA模型在构建的过程中通常要求决策单元DUMi必须具有投入变量,因此,为了保证决策的公平性,在模型的构建过程中本文赋予所有决策单元相同的虚拟输入变量sτ,那么基于语言偏好关系A=(aij)n×n,可以得到如下的DEA投入产出表(见表1)[19,34]。 于是可以构建如下产出导向的DEA模型用于计算决策单元DUMi(i∈N)(即方案xi)的相对效率: maxβi (18) 在模型(18)中,本文基于所有决策单元构建了一个虚拟的组合单元,其中up表示构建虚拟组合单元是决策单元DUMi所占的比例。模型(18)表示虚拟组合单元在最多消耗与决策单元DUMi相同投入量sτ的前提下,至少输出决策单元DUMi产出的βi≥1倍。 maxβi (19) (20) (21) 通过结合公式(20)和(21)可得 (22) 则有 (23) 再将公式(23)带入到公式(22)可得 (24) 综上,定理4结论成立。 对于给定的语言偏好关系A=(aij)n×n,接下来将运用一致性改进算法和权重确定方法得到决策方案的可靠排序,最终遴选出最优方案。 算法 II Input: 原始语言偏好关系A=(aij)n×n. 第二阶段:根据最优化模型(18)的目标函数值和定理4,确定方案的排序权重w=(w1,w2,…,wn)Τ。 第三阶段:依据排序权重wi(i∈N)的大小对方案xi(i∈N)进行优劣排序,并输出选择最佳方案。 第二阶段:利用MATLAB计算最优化模型(18)的最优目标函数值,并运用定理4得到供应商对应的排序权重向量:w=(w1,w2,w3,w4)T=(0.5413,0.2313,0.1575,0.0699)T。 第三阶段:由于w1>w2>w3>w4,所以x1≻x2≻x3≻x4,于是综合性能最佳的供应商为x1。 基于一致性局部调整策略和DEA的语言决策模型不仅能够在最大程度保留原始决策信息的基础上将原始语言偏好关系调整为具有满意乘性一致性的语言偏好关系,而且能够通过DEA模型得到方案的排序权重。接下来,为了说明本文方法的有效性,将运用现有的语言决策方法处理上述问题。 Xu Zeshui[30]基于提出的语言算术平均算子处理上述问题的大致过程为:首先运用语言算术平均算子计算得到四个供应商对应的综合语言偏好信息: a1=s4.350,a2=s4.075,a3=s3.300,a4=s4.275。 因为a1>a4>a2>a3,所以供应商的优劣顺序为x1≻x4≻x2≻x3,并且综合性能最佳的供应商为x1。 Dong Yucheng等[31]研究了加行一致性语言偏好关系的改进算法,以使得改进后的语言偏好关系达到一致性阈值水平。运用文献[31]中算法处理上述供应商选择问题的主要步骤如下: V(0)= 步骤4:利用语言算术平均算子计算四个供应商对应的综合语言信息分别为: 针对不具有满意加性一致性的不确定二元语言偏好关系,文献[32]首先提出了一种加行一致不确定二元语言偏好关系的构建方法,然后设计了新的加性一致性迭代算法对原始的不确定二元语言偏好关系进行提升,最后运用二元语言算术平均算子得到供应商的综合偏好信息。运用文献[32]中算法4.1处理上述供应商选择问题的主要步骤如下: 步骤1’:将语言偏好关系A=(aij)4×4转化为如下二元语言偏好关系B=(bij)4×4: B= 步骤4’:运用二元语言算术平均算子计算得到四个供应商对应的综合语言信息分别如下: 分析上述对比实验过程和结果,本文提出的基于一致性局部调整策略和DEA的语言决策模型具有以下优势: (1)运用本文建立语言决策模型计算得到的最佳供应商与利用文献[30]、文献[31]和文献[32]中算法4.1得到的决策结果相同,这说明了提出的语言决策模型是合理的。 (2)众所周知,运用不具有满意一致性的语言偏好关系容易得到非一致的决策结果。然而,文献[30]在没有对语言偏好关系进行一致性检测的情况下,直接运用语言算术平均算子对供应商的所有语言决策信息进行融合。相反,本文提出的模型首先对原始给定的语言偏好关系的一致性进行检测和改进,然后计算供应商的排序权重向量和决策结果。因此,本文提出的语言决策模型相较于文献[30]中的决策方法更为有效。 针对决策信息为语言变量的决策问题,本文首先研究构造乘性一致语言偏好关系的方法,为了尽可能保留原始决策信息,引入局部调整策略,设计了一种乘性一致性改进算法,使得改进后的语言偏好关系具有满意乘性一致性,并证明算法的收敛性。随后,基于DEA模型建立了最优化模型,进而确定方案的排序权重向量。最后,构建一个基于一致性局部调整策略和DEA方法的语言决策模型,从而得到合理可靠的决策结果。 本文仅考虑了决策过程中专家提供的决策信息完全可知的情况,针对专家因某些因素而没有给出决策信息的情况,即如何针对不完全语言偏好关系构建合理有效的决策模型尚有待进一步研究。同时,在语言偏好决策模型的构建过程中运用传统自评优先DEA模型只能分辨出决策单元是DEA有效还是非有效的,可能导致不具备对决策单元(决策方案)进行排序的能力,因此如何运用交叉效率DEA模型来克服传统自评优先DEA模型的不足,设计基于交叉效率DEA模型的语言偏好决策方法可以作为今后的研究方向。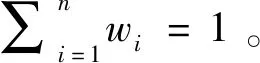
3 语言偏好关系的一致性局部调整算法
3.1 乘性一致语言偏好关系的构造
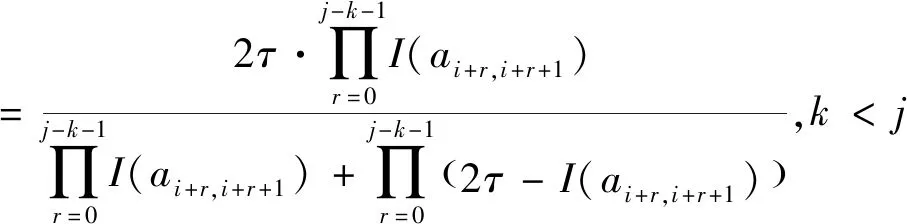
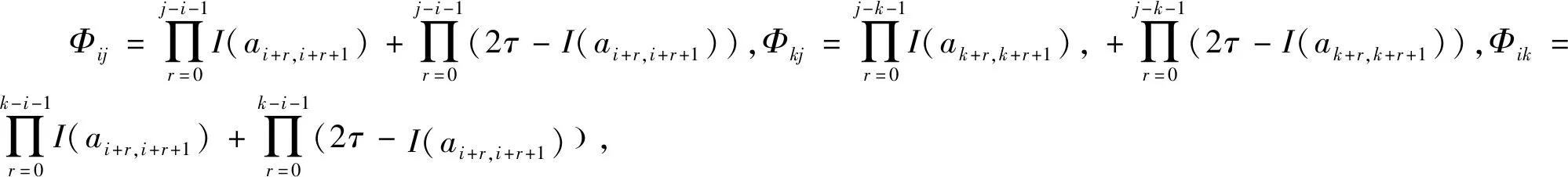
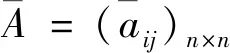
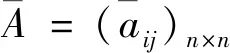
3.2 基于局部调整策略的一致性改进算法
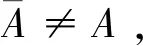
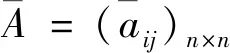

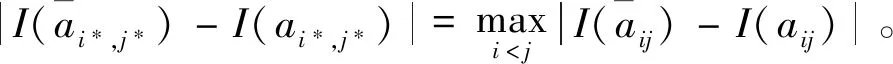

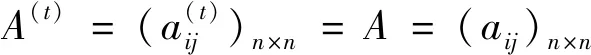
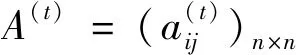
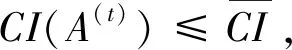
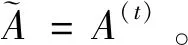
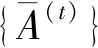
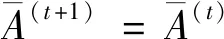
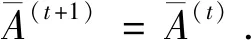
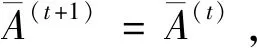
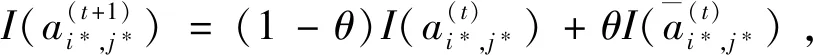
4 语言决策模型
4.1 基于DEA的排序权重确定方法

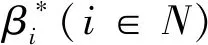


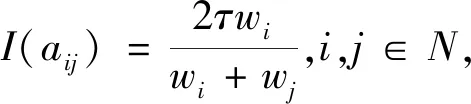
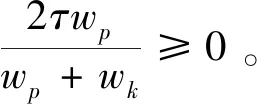

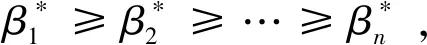

4.2 语言决策模型
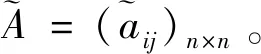
5 数值实验与对比分析
5.1 数值实验
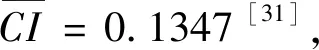
5.2 对比分析
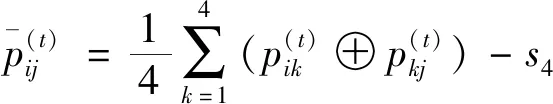
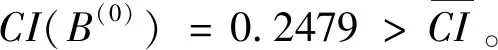
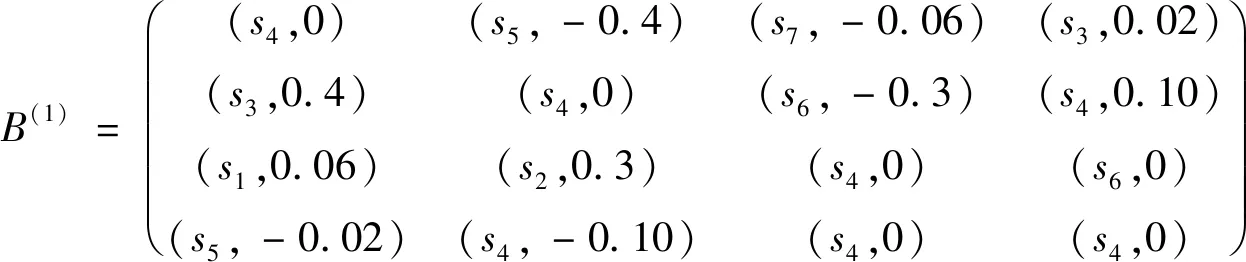
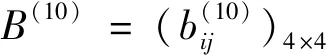
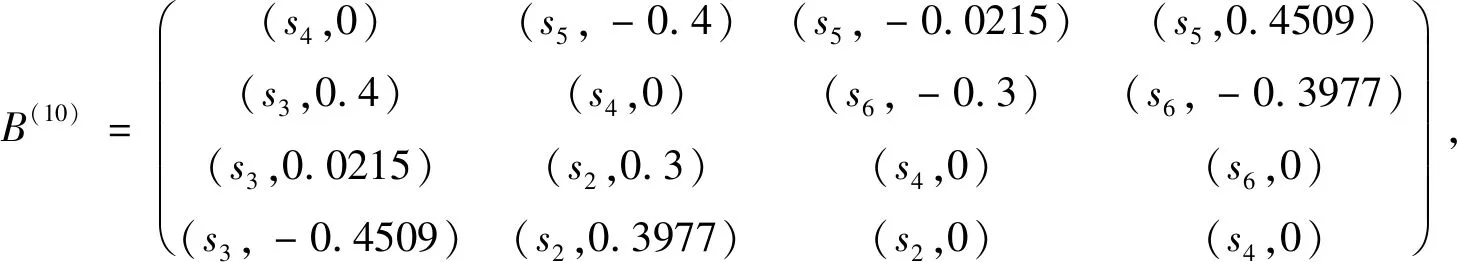
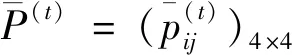
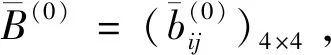
6 结语
