一个可积的逆空时非局部Sasa-Satsuma方程*
2020-01-16宋彩芹朱佐农
宋彩芹 朱佐农
1) (上海理工大学理学院, 上海 200093)
2) (上海交通大学数学科学学院, 上海 200240)
本文给出了一个可积的逆空时(逆空间-逆时间)非局部Sasa-Satsuma方程.建立了这个方程的Darboux变换,并且构造了这个逆空时非局部方程在零背景条件下的孤子解.
专题:非线性物理
1 一个可积的逆空时非局部Sasa-Satsuma方程
耦合的Sasa-Satsuma系统
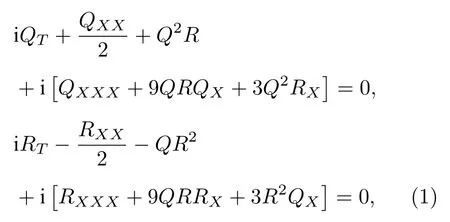
是一个非线性可积系统.这个系统在约化条件R(X,T)= ±Q∗(X,T)下转化为经典的Sasa-Satsuma方程[1−14],
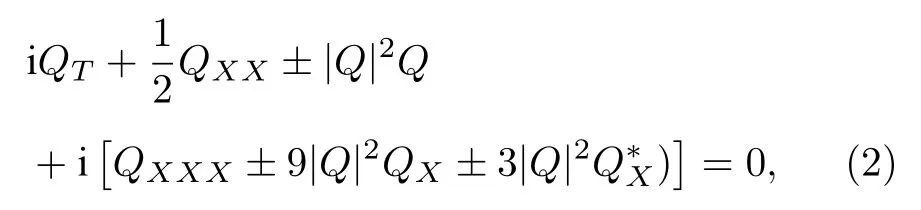
这是一个可积的高阶非线性薛定谔方程.这个方程可以用来描述光纤中飞秒脉冲的传播[2,3].
最近, Ablowitz和Musslimani[15]给出了一个逆空间的可积非局部NLS方程,

这个逆空间的可积非局部NLS方程引起了人们对这类非局部可积非线性系统的极大研究兴趣.若干逆空间、逆时间或逆空时非局部可积方程被提出并被研究[15−24].作者在文献[20]中研究了一个逆空时可积非局部Sasa-Satsuma方程:
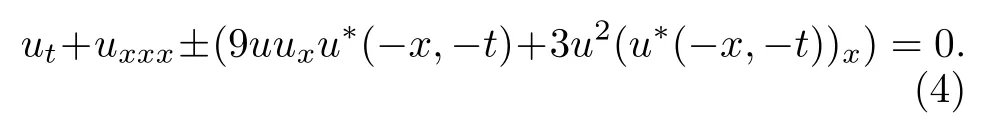
我们注意到这样一个事实: 对于系统(1), 如果做约化R(X,T)=Q(−X,−T) , 则可得到如下逆空时非局部Sasa-Satsuma方程:

在变换
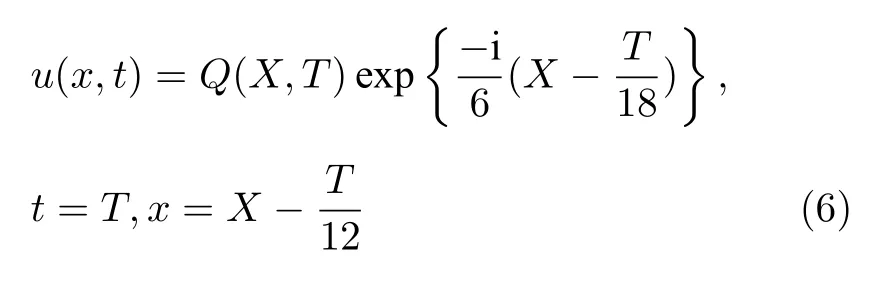
下, 逆空时非局部Sasa-Sasuma方程(5)转化为如下形式:
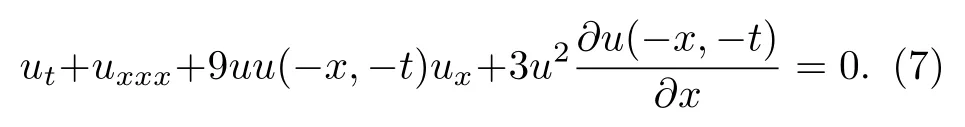
显然, 方程(7)也可以看作为一个逆空时非局部mKdV型方程.本文的主要目的是建立逆空时非局部 Sasa-Sasuma方程 (7)的 Darboux变换, 并给出这个方程的孤子解.
2 逆空时非局部Sasa-Satsuma方程(7)的Darboux变换
我们注意到方程(7)可以从系统
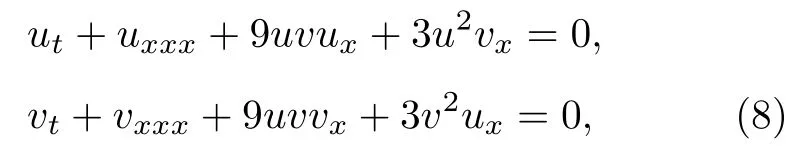
通过约化v=u(−x,−t) 而得到.Sasa-Satsuma 系统 (8)和耦合系统 (1)是等价的.事实上, 在变换
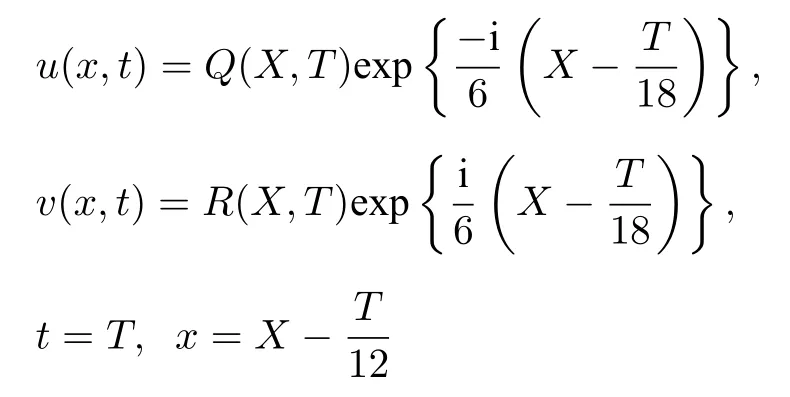
下, 这两个系统可以相互转化.对于耦合Sasa-Satsuma系统 (8)在不同的约束条件下可以化为不同的方程: 当v=u时, 系统 (8) 化为 mKdV 方程; 当v=u∗时, 系统 (8) 化为一个复的 mKdV 型方程即经典的Sasa-Satsuma方程.Sasa-Satsuma方程 (8)是 Lax 可积的.事实上, 系统 (8)可由如下的线性谱问题
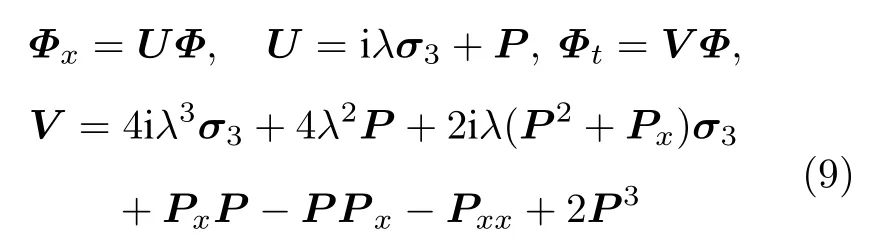
的可积性条件Ut−Vx+UV−VU=0得到,其中
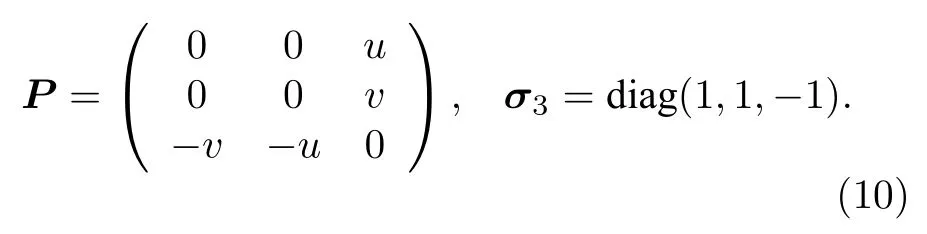
我们用Φ(x,t;λj) 来表示线性谱问题(9)在谱参数λ=λj下的特征向量函数.令Θj=Φ′(x,t;λj)M,那么可以直接验证
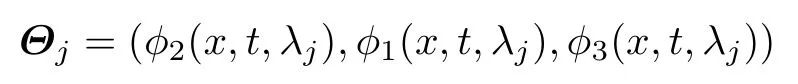
是线性谱问题(9)的伴随问题
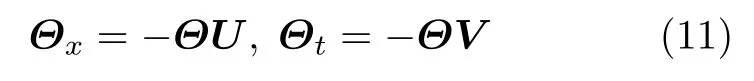
在谱参数λ=−λj下的特征函数, 这里上标 ′ 表示矩阵的转置, 矩阵M是
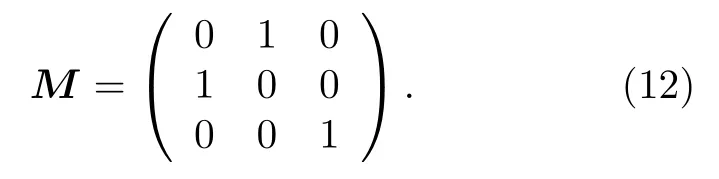
将Φ(x,t;λj) 和ϕl(x,t;λj) 分别简记为Φj和ϕj,l.类似于文献[20], 我们可以获得Sasa-Satsuma方程(7)的 Darboux变 换.首 先 给 出 (8)式 的 双Darboux变换.作如下特征函数的变换:
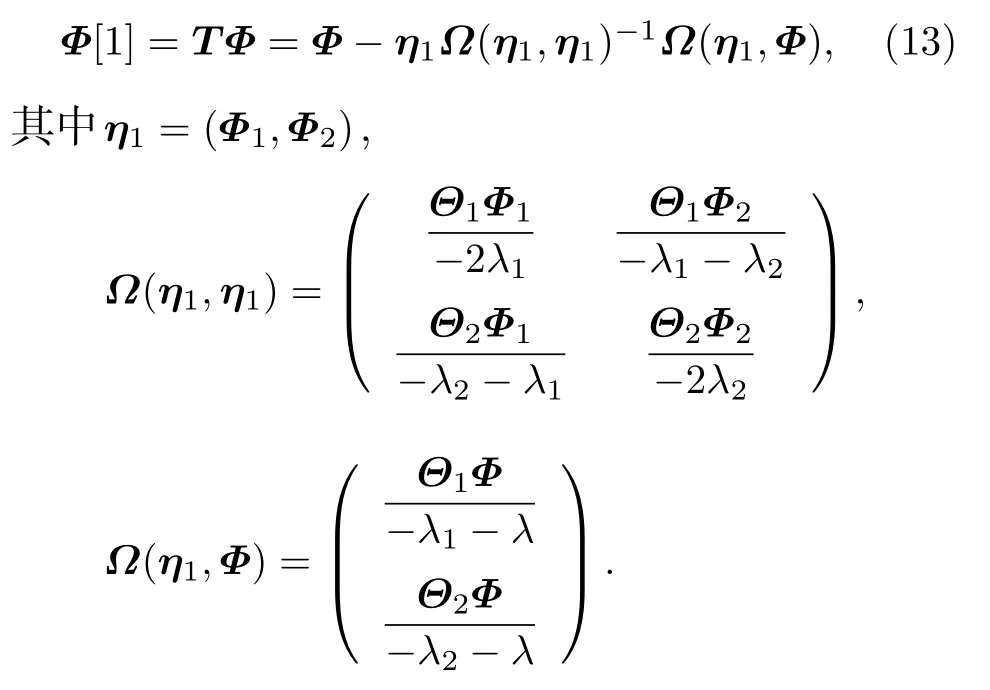
则联系于耦合的Sasa-Satsuma系统 (8)的线性谱问题(9)变换为
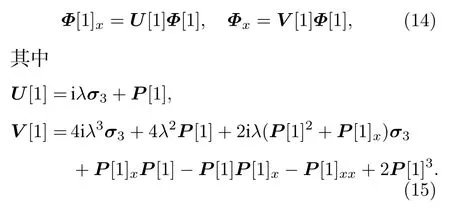
我们期望矩阵P[1] 与矩阵P有完全相同的结构.可以验证如果矩阵P[1] 中的u[1],v[1] 与矩阵P中的u,v有如下关系:
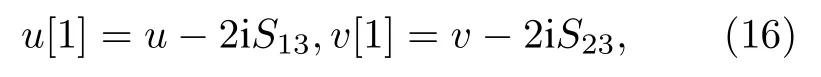
如果令矩阵P中的v=u(−x,−t) 并选取适当的参数使得S23=S13(−x,−t) , 那么P[1] 中的v[1]就等于u[1](−x,−t) .从而u[1] 与u的关系实质上就是逆空时非局部Sasa-Satsuma方程(7)的Bäcklund 变换.u[1] 是这个逆空时非局部 Sasa-Satsuma方程的解.
进一步, 可以给出耦合Sasa-Satsuma系统(8)的n次双Darboux变换.令
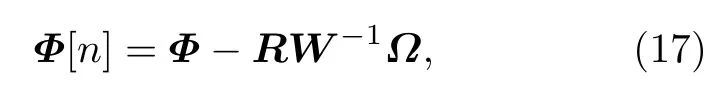
其中R=(η1,η2,···,ηn) 并且
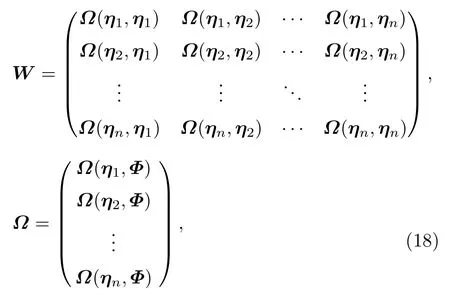
其中ηk=(Φ2k−1,Φ2k) ,
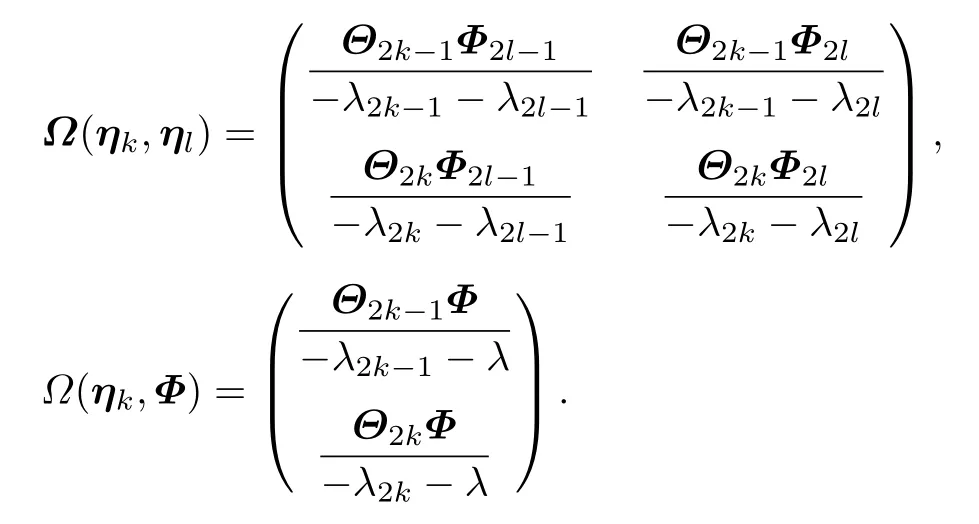
变换后位势函数u[n] 和v[n] 可以由矩阵P[n] 与矩阵P之间的关系
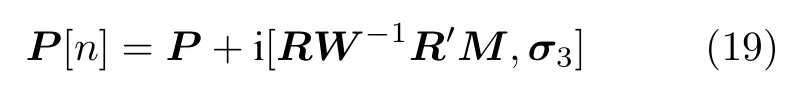
给出.设a,b是一个 2n阶行向量, 那么根据等式关系
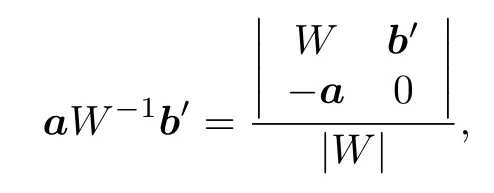
可以得到
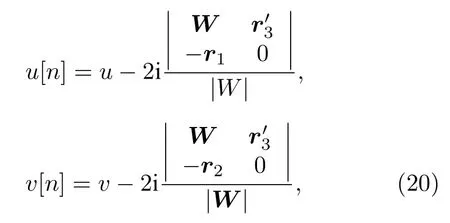
其 中rl=(ϕ1,l,ϕ2,l,···,ϕ2n−1,l,ϕ2n,l),l=1,2,3.需要指出, 文献[5]给出了Sasa-Satsuma方程(即方程(8)中取v=u∗)的Darboux变换, 但没有给出 高 阶 Darboux变 换.这 里 给 出 了 Sasa-Satsuma 系统 (8)的高阶双 Darboux 变换.在约化v=u∗下 , 取及特征函数Φ2j=即可获得Sasa-Satsuma方程的高阶Darboux变换.
3 逆空时非局部Sasa-Satsuma方程(7)的解
借助于Darboux变换, 我们将构造方程(7)的解.方程(7)有指数形式的解u=reκ(x−(κ2+6r2)t) ,其中r和k是任意的实数.特别地,u=0 是一个解.解对应的线性谱问题得到在谱参数λ=λj时的特征函数为
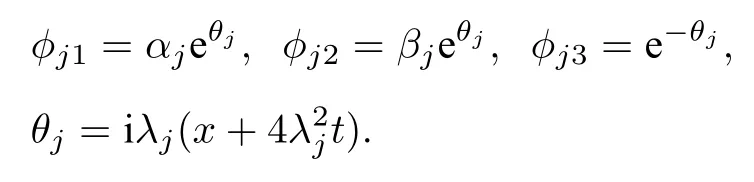
用 Darboux 变换, 获得u[1] 和v[1] 如下:
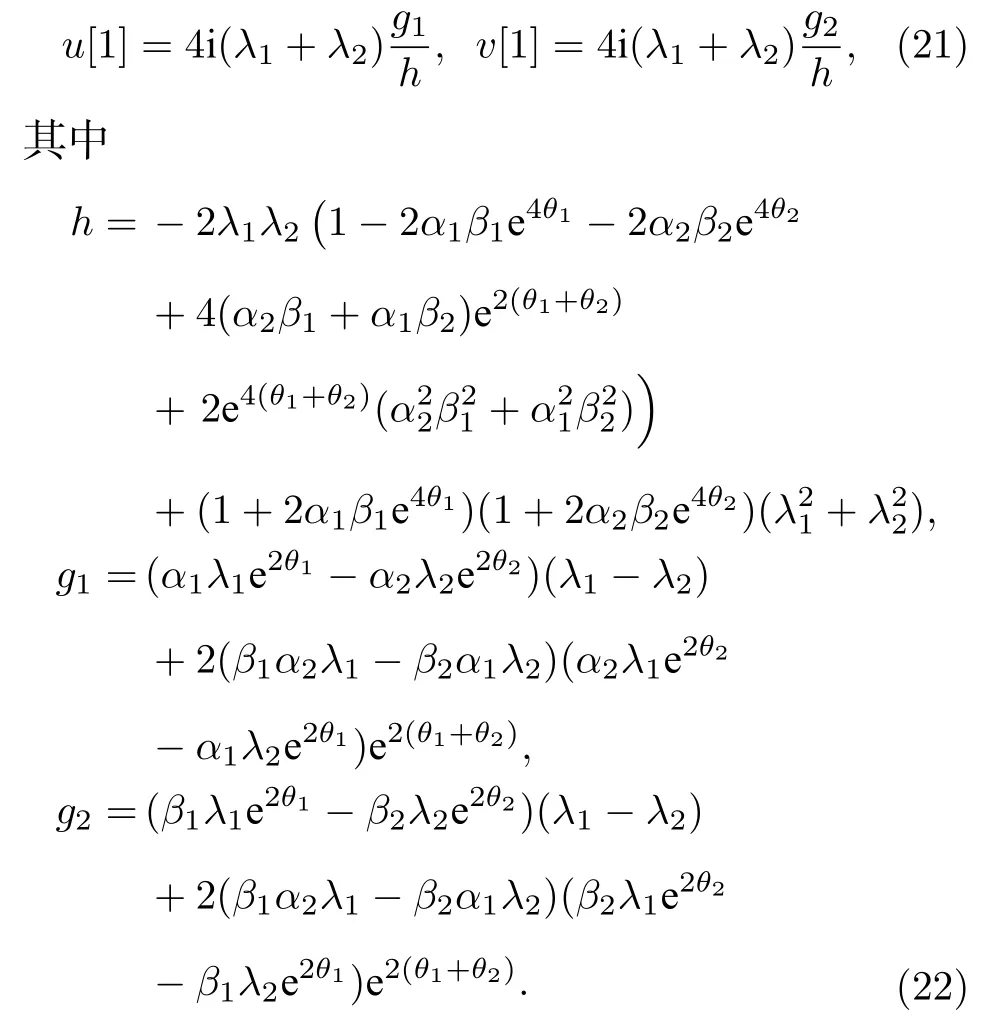

显然, 要得到逆空时非局部方程(7)的解, 需要选择适当的参数, 使得v[1]=u[1](−x,−t) .经过分析,我们发现在如下几种参数情况下:
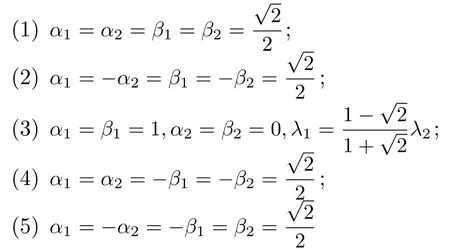
有v[1]=u[1](−x,−t) .从而逆空时非局部方程(7)的解被构造.对于情形 (1)—(3), 有u(x,t)=u(−x,−t), 而对于情形 (4)—(5)有u(x,t)= −u(−x,−t).我们给出了对应于情形(1)—(3)的解u(x,t) 的图, 如图1 所示.
值得指出, 经典的Sasa-Satsuma方程有一个显著的特征, 即存在双峰孤波解.对于逆空时非局部可积方程(4), 我们也给出了类似的双峰孤波解.但对于本文研究的逆空时非局部可积方程(7), 并没有发现这样的双峰孤波解的存在.从这个意义上说, 逆空时非局部可积方程(4)和方程(7)确有不同的性质.逆空时非局部可积方程(7)值得进一步研究.
