基于改进卡尔曼滤波算法的路面构造深度计算方法

娄月新 陈圣迪 陆 键 郎 洪

(1同济大学道路与交通工程教育部重点实验室, 上海 201804)(2上海海事大学交通运输学院, 上海 201306)

道路表面的构造深度是评定路面粗糙度和抗滑性的重要指标[1].随着道路使用和自然环境的影响，较小的路面构造深度会大大降低道路的安全性，提升交通事故发生的概率.因此，对路面构造深度的准确测量和计算是判断道路安全性的重要手段之一，为道路安全性能的改善提供理论依据.

目前，对路面构造深度的检测方法主要分为接触式检测法和非接触式检测法[2-3].接触式检测法通过测量设备直接测得路面的平均构造深度(mean texture depth, MTD)，主要以铺砂法为主，其中又包括手工铺砂法和电动铺砂法，该类方法目前仍作为我国检测和校准构造深度的标准测量方法[4].非接触式检测法则是通过自动化测量设备获得路面的平均剖面深度(mean profile depth，MPD)或传感器测量构造深度(sensor mean texture depth，SMTD)，该类方法以车载激光检测仪为主.美国材料与试验协会[5](American society for testing materials, ASTM)和澳大利亚道路研究局[6](Australian road research board, ARRB)分别给出了MPD和SMTD的测量和计算方法，我国的标准规范[7]也对2个指标的测量和计算方法进行了详细的定义，建立了较合理的计算过程.然而，路面环境中的多种噪声干扰和传感器的系统测量误差会很大程度上影响最终的构造深度计算结果[8]，因此非接触式检测法计算的MPD和SMTD结果通常需要经过与铺砂法计算值进行相关分析，并建立对应的数学模型进行转换后方能使用，ASTM在标准中规定了MPD与MTD为线性转换模型，表征为DMTD=0.2+0.8DMPD，其中DMTD为铺砂法MTD计算值，DMPD为MPD计算值；ARRB依照ASTM标准也规定了SMTD和MTD的转换模型.但由于路面及检测方法的差异性，对应的转换模型也会存在差异，大量的试验结果[9-13]表明线性转换模型的斜率通常在0.5～1.2范围内，截距在-0.3～1.0之间.因此，对于不同的测量设备和路面材料特性，模型的建立也需要对应的试验数据来进行检验和修正，从而进一步提升测量结果的精度.

综上，路面构造深度的检测方法主要以铺砂法和激光检测法为主.但铺砂法需要大量的人力和时间，检测效率低；激光检测法弥补了铺砂法的缺点，但在实际检测中由于激光传感器测量误差及环境中各类噪声的影响，需要研究合理的算法对激光测量数据进行滤波和计算才能确保测量的准确性.目前较为普遍采用的是滑动滤波算法，该算法采用均值方法对给定滑动长度区间内的数据中心点进行修正[4]，但该算法去噪结果较为粗糙，不能保留路面纵断面更多的细节.此外，不同的路面材料具有不同的构造深度特性，其转换模型也随之不同，需要进一步进行研究.基于以上不足，本文提出基于改进卡尔曼滤波(Kalman filter, KF)算法的路面构造深度计算方法，该方法对获取的激光测量高程数据进行初步筛选及插值修正，建立改进KF算法进行滤波去噪，进而通过MPD计算模型获得路面MPD值，并依据AC-13和SMA-13两种沥青混凝土路面材料试验样本的标准铺砂法计算结果建立了MPD与MTD线性转换模型，最后通过与滑动滤波算法的对比试验验证了该方法具有更高的测量精度.计算结果具有较高的重复性和相关性，在检测方法研究和实际检测应用中有一定的价值.

1 路面MPD计算模型

1.1 异常值筛选及修正

在激光检测法中，通常采用激光距离传感器来获得路面的纵断面高程值.但在实际检测中由于路面的复杂性、传感器测量误差、检测系统的机械震动和测量过程中人为等因素，通过激光测得的路面高程值会存在大量的噪声及一些与大部分测量值偏差极大的异常点[14]，因此需要对高程点的检测值进行预处理.本文通过对采集的数据进行统计分析发现，激光测量的路面纵断面高程值呈高斯分布，如图1所示.因此，对于测量的样本数据建立t检验进行异常值识别筛选[15].

图1 高程值概率分布

采集的一组高程值样本矩阵X={X1,X2,…,Xn}服从高斯分布，其中n为高程值个数，对Xi(i=1,2,…,n)构建原始假设H0：Xi(i=1,2,…,n)属于异常点；备择假设H1：Xi(i=1,2,…,n)不属于异常点.建立检验统计量T为

(1)

(2)

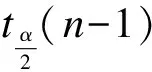
(3)

式中，Oi为筛选出的异常值；Oi-1为异常值的左邻正常值；Oi+1为异常值的右邻正常值.

1.2 改进KF算法

数据预修正后需对修正后的数据进行滤波去噪，目前采用的滑动滤波算法[16]的缺点在于进行第1次滤波时，滤波窗口内的采样点均为未滤波的原始采样点，即包含了采样噪声，因此在之后的滤波过程中仍然包含了部分噪声，不能达到良好的去噪效果.KF算法是时域滤波中最优化自回归数据处理算法，是将信号的变化规律用线性数学模型进行表征，采用递归的方式实时计算预测值和观测值之间的最小均方误差来对观测的数据进行更新，从而实现去噪并获得测量点的最优估计[17-20].对于本文研究对象而言，道路表面的纵断面由于集料等因素的影响并非完全的线性变化，因此传统KF算法受到了限制.本文通过大量的试验分析和计算发现，由于检测过程中路面构造深度测量系统的采样间隔极小(1 mm)，路面的高程变化在极短间距L(本文中L取50 mm，即采样点数量N为50)内具有线性变化趋势，其可用线性模型y=ax+b进行拟合表征，其中a和b为线性模型参数变量，如图2所示.因此，本文对传统KF算法进行改进，在预测过程中利用最小二乘法[21]建立动态线性回归模型进行预测，并在更新过程中采用限制增益法来抑制滤波过程的发散，从而实现对测量数据的准确滤波去噪.其算法过程分为如下2步.

图2 路面纵断面剖面

1) 将纵断面采样距离以间距L划分为若干个分析单元，则对于每个分析单元中的高程值xp(p=1,2,…,N-1)和xq(q=2,3,…,N)，其线性回归模型可表征为

xq=β0+β1xp

(4)

式中，回归系数β0和β1计算公式为

(5)

2) KF算法的系统模型包含状态方程和观测方程，即

xk=Fkxk-1+Bkuk+wk

(6)

zk=Hkxk+vk

(7)

式中，xk为k时刻系统所在状态矩阵；Fk为系统状态转移矩阵；Bk为控制变量转移矩阵；uk为控制变量；wk为系统预测噪声，服从高斯分布常用其协方差矩阵Q表征；zk为系统观测矩阵；Hk为观测转移矩阵；vk为系统测量噪声，服从高斯分布常用其协方差矩阵R表征.

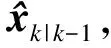
① 进行初始化定义：初始状态值xk-1=zk-1，初始均方误差为Pk-1=1.

1.3 MPD计算模型

MPD是指在特定长度区间内的断面深度的平均值，与MTD有着良好的相关关系，通过对应的转换模型能够间接地获得MTD值，是非接触式检测法中计算的指标之一.其计算原理如图3所示.

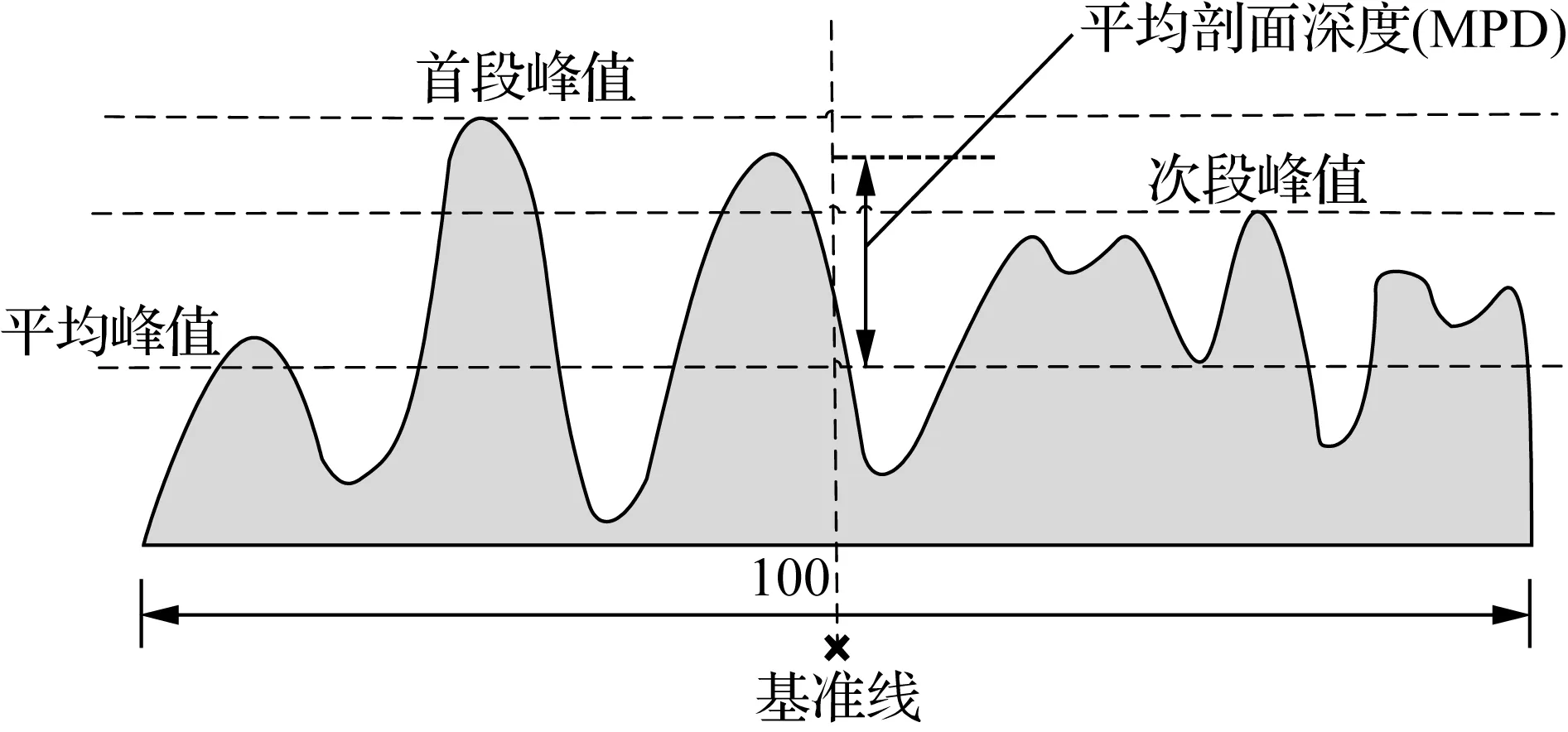
图3 MPD计算原理图(单位：mm)

MPD计算模型的主要过程是将测量路段以100 mm为单位划分为M个计算单元，每个计算单元前50 mm和后50 mm两个断面高程峰值的平均值与该100 mm计算单元高程平均值之差为该计算单元MPD值，则各计算单元MPD值的均值为整个路段的MPD值.本文基于ASTM和我国JTG E60—2008规范标准[3-4]，利用处理和滤波后的路面高程值来计算MPD，即

(8)

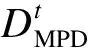
2 试验方案

2.1 试验样本

不同的路面材料结构具有不同的路面纹理构造，为了减小由于单一样本造成的误差，本文选取SMA-13和AC-13两种沥青混凝土路面作为试验样本，每种路面类型选择5条，每条长度50 m.试验样本地理位置信息如表1所示，样本表面形态如图4所示.

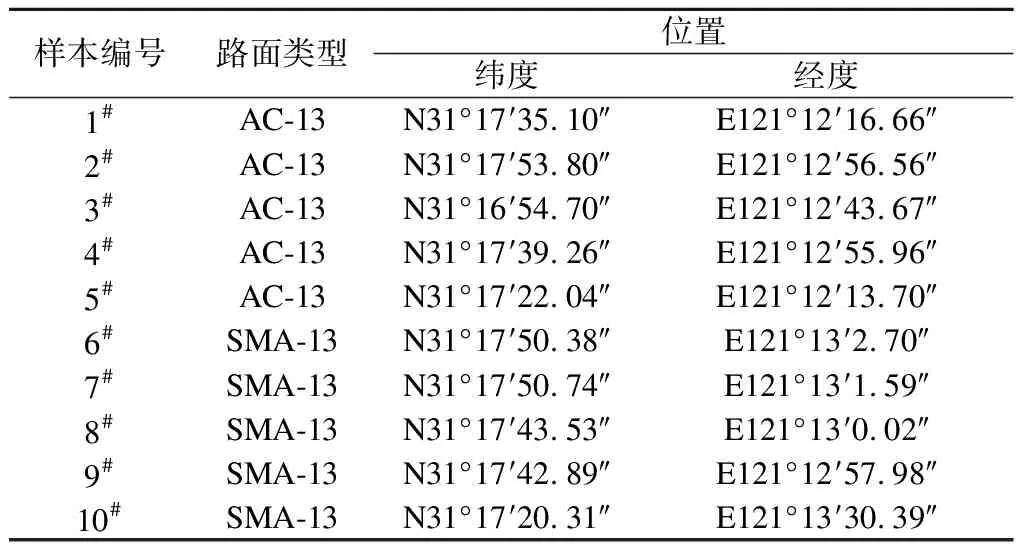
表1 试验样本路段地理信息

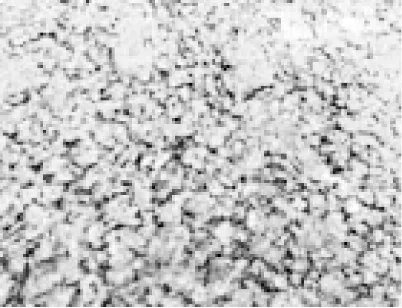
(a) 1#样本

(b) 2#样本

(c) 3#样本

(d) 4#样本

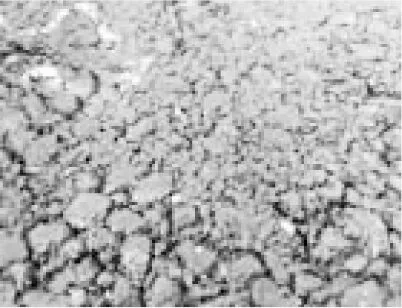
(e) 5#样本

(f) 6#样本

(g) 7#样本

(h) 8#样本

(i) 9#样本

(j) 10#样本

2.2 数据获取

采用手推式激光路面纵断面剖面仪和铺砂法分别对样本路段进行数据采集.手推式激光路面纵断面剖面仪是一种基于无线蓝牙传输和高精度激光距离传感器的路面纵断面高程测量系统，通过高精度激光距离传感器可每隔1 mm获得一个路面纵断面高程值.在手推式激光测量仪采集数据后，以5 m作为采样间距沿路面纵断面相同的位置参照ASTM E965-15标准规范[23]中的相关要求进行铺砂法测量，现场试验如图5所示.

3 试验结果及分析

3.1 试验结果

对铺砂法及改进KF算法、滑动滤波算法计算得出的MTD和MPD值进行统计，如表2所示.可以看出，由于路面受到不同程度的磨损，因此同一种路面类型具有不同的构造深度，表现为AC-13沥青混凝土样本的计算结果在0.729～1.103 mm之间，SMA-13沥青混凝土样本的计算结果在0.934～1.424 mm之间.此外，由于不同计算方法的差异性，滑动滤波算法的计算结果均高于铺砂法计算结果，而改进KF算法的计算结果除5#和10#两个样本之外，其余均高于铺砂法计算结果.

(a) 手推式激光纵断面剖面仪测量

(b) 铺砂法测量

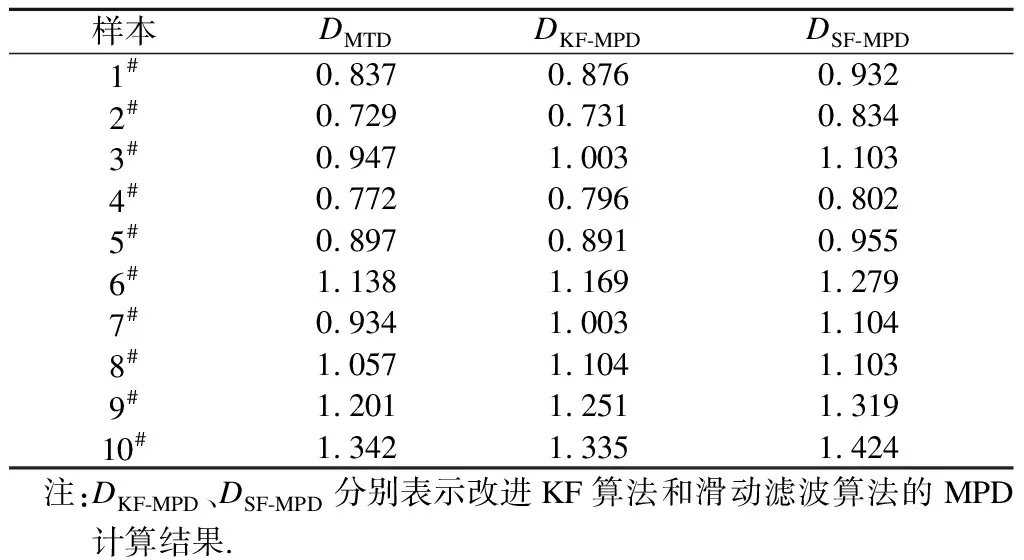
表2 改进KF算法、滑动滤波算法及铺砂法计算结果

进一步选取1#、2#、6#和7#四个样本，分别用手推式激光纵断面剖面仪和铺砂法进行了10次重复性数据采集，并分别计算10次的DMTD、DKF-MPD和DSF-MPD值，计算结果如表3所示.

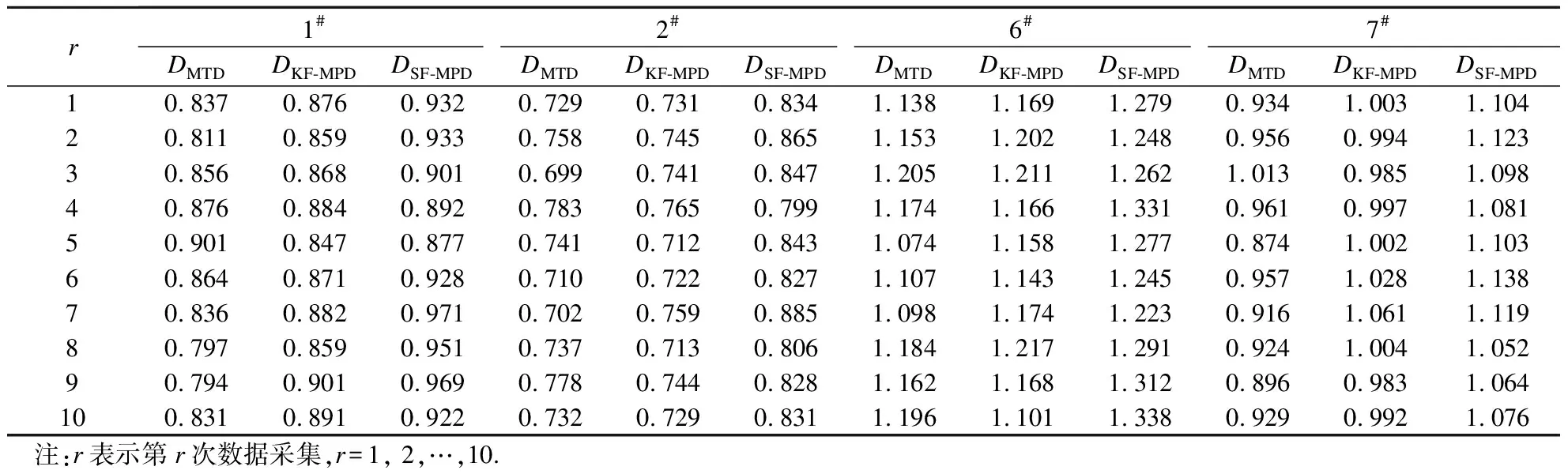
表3 1#、2#、6#和7#四个样本的重复性计算结果

3.2 滤波算法试验结果分析

由于空间限制，以1#和6#样本为例，将本文提出的改进KF算法与传统的滑动滤波算法进行比较分析，两者的滤波结果如图6所示.

由图6可以看出，改进KF算法与滑动滤波算法对传感器采集的测量值均达到了滤波效果，其中滑动滤波算法使得路面纵断面剖面曲线更加的平滑，而改进KF算法在去除噪声的同时，更多地保留了道路表面的细节，相比滑动滤波算法的结果更符合实际道路表面状况.为了进一步验证改进KF算法计算结果，选择均方误差(mean square error, MSE)和平均绝对百分比误差(mean absolute percent error, MAPE)两个统计量来进行误差分析，其中MSE是检验测量值与真实值之间的偏差，而MAPE则是对测量方法精度的一种度量[24]，其模型为

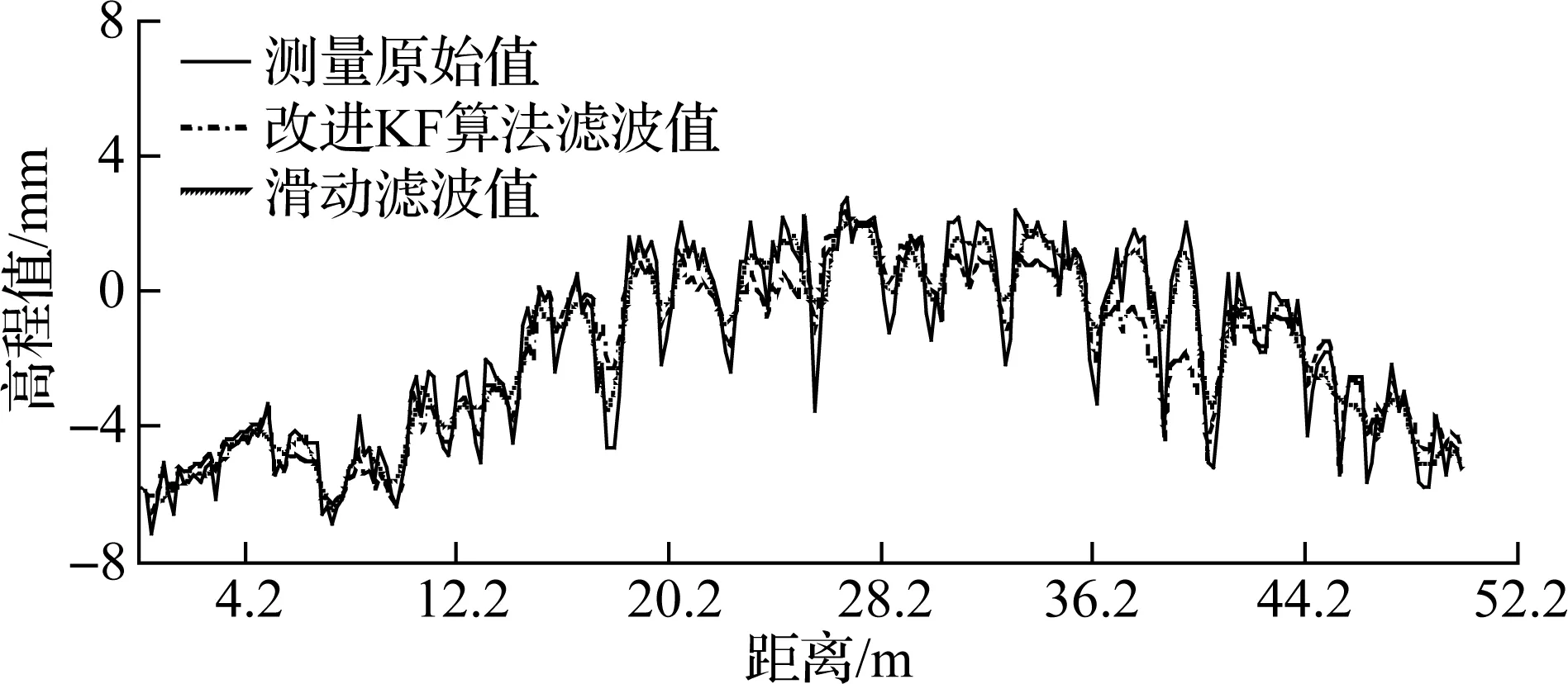
(a) 1#样本

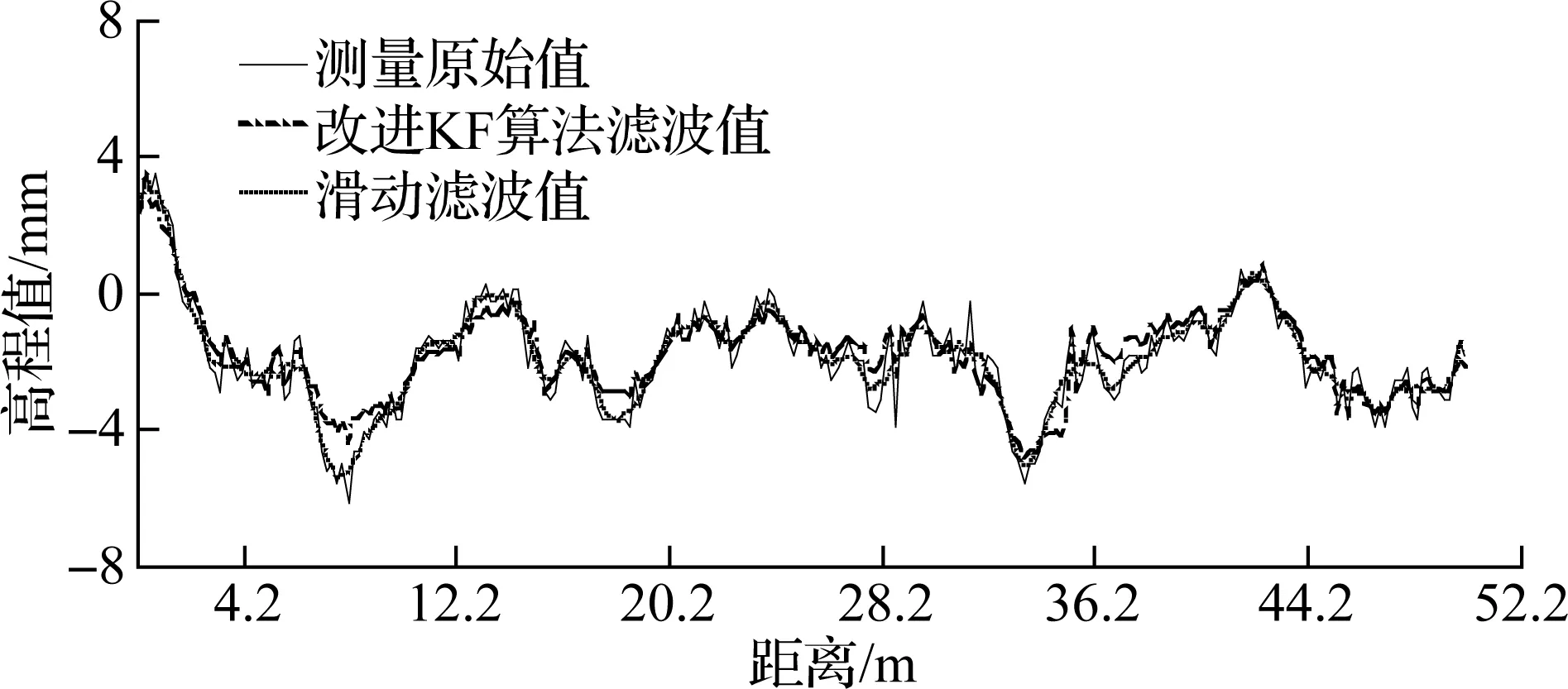
(b) 6#样本

(9)

式中，VMSE为MSE值；VMAPE为MAPE值；Ac为第c个样本真实值，本文中为铺砂法计算结果；Fc为第c个样本测量值，本文中为改进KF算法或滑动滤波算法计算结果；B为测量的样本数，本文中B=5.以铺砂法的测量结果为标准，计算改进KF算法和滑动滤波算法的MSE及MAPE值，结果如表4所示.

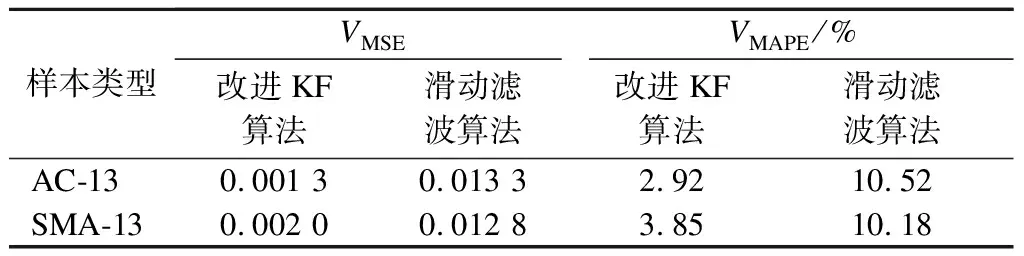
表4 改进KF算法和滑动滤波算法的对比分析

由表4可以看出，对于AC-13和SMA-13两种路面类型样本，改进KF算法的MSE计算结果分别为0.001 3和0.002 0，MAPE值计算结果分别为2.92%和3.85%，均小于滑动滤波算法，表明改进KF算法计算得出的剖面深度值与铺砂法计算结果之间的偏差更小，精度更高，相比滑动滤波算法的计算结果更接近于标准的铺砂检测法.

3.3 重复性试验结果分析

对表3数据进行定量分析，选择标准偏差(standard deviation, Std)和变异系数[25](coefficient of variation, CV)两个统计量来检验计算结果的稳定性和变化强度，二者都是衡量一组数据分布离散程度的标准，其中变异系数是无量纲指标，能够消除测量尺度和量纲对分析的影响，从而更客观地反映数据的离散程度.指标计算公式如下：

(10)

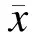
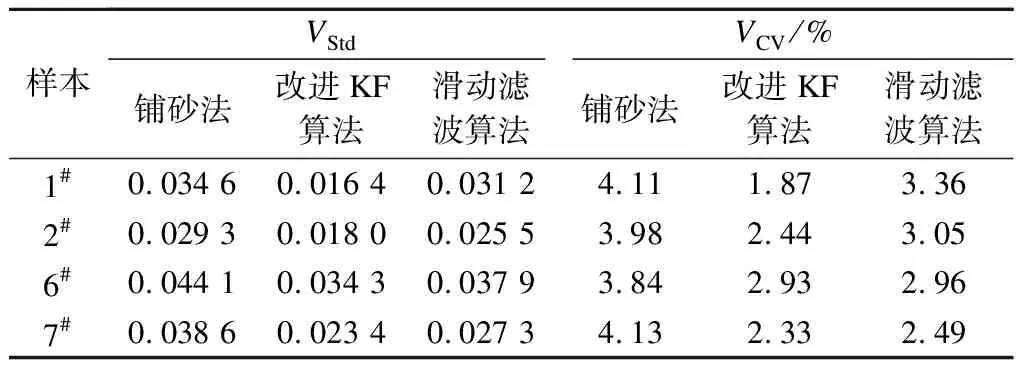
表5 重复性计算结果分析

由表5可以看出，铺砂法的VStd和VCV值最大，表明铺砂法存在大量的误差及不稳定性，其重复性较低；而改进KF算法相比滑动滤波算法具有更低的VStd和VCV.特别地，对于AC-13样本类型，改进KF算法与滑动滤波算法的VStd和VCV差异较大，而对于SMA-13样本类型差异较小，表明改进KF算法对AC-13样本类型的计算稳定性具有更大的优势.同时，改进KF算法的VStd分别为0.016 4、0.018 0、0.034 3、0.023 4，VCV分别为1.87%、2.44%、2.93%、2.33%，均符合我国JTG/T E61—2014标准规范[7]中的要求(<5%)，算法具有较强的稳定性.

3.4 相关性试验结果分析

为了进一步分析改进KF算法与滑动滤波算法的差异性，并建立不同路面材料结构的构造深度转化模型，对2种滤波算法的计算结果和铺砂法计算结果进行t检验分析[26]，结果如表6所示.

由表6可知，对于AC-13和SMA-13两种路面类型，改进KF算法的测量结果具有极低的p值，分别为0.005和0，意味着对于t检验将在显著性水平0.01上拒绝原始假设(0.005、0<0.01)，即改进KF算法计算结果与铺砂法测量结果没有差异，具有相关性.同时，对于AC-13和SMA-13两种路面类型铺砂法和改进KF算法的相关系数(correlation coefficient)R分别为0.975和0.995，均符合我国JTG/T E61—2014标准规范[7]中的要求(>0.95)，证明本文改进KF算法与铺砂法具有强相关性.而对于AC-13和SMA-13两种路面类型滑动滤波算法与铺砂法的t检验p值分别为0.021和0.014，均高于改进KF算法结果，且在显著性水平0.05上具有相关性，R分别为0.932和0.949.因此，改进KF算法计算结果更优于滑动滤波算法.进而将改进KF算法和铺砂法计算结果利用SPSS软件进行线性回归分析建模，模型拟合结果如图7所示.

表6 2种滤波算法计算结果与铺砂法计算结果的t检验分析

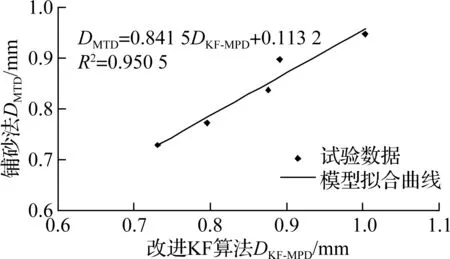
(a) AC-13样本

(b) SMA-13样本

由图7可知，对于AC-13和SMA-13两种路面类型样本改进KF算法与铺砂法的决定系数(coefficient of determination)R2分别为0.950 5和0.989 3，其中SMA-13样本类型的R2更高，表明所建立的回归模型具有较高的拟合优度.此外，AC-13类型样本的线性转换模型的斜率和截距分别为0.841 5和0.113 2，SMA-13样本类型的线性转换模型的斜率和截距分别为1.185 1和-0.255 0，与美国ASTM标准中模型相比，斜率均高于0.8且截距均低于0.2，结果表明不同路面类型样本具有不同的转换模型.

4 结论

1) 针对目前构造深度计算模型精度不高、滤波方法较粗糙的问题，本文提出了基于改进KF算法的数据滤波方法，与传统滑动滤波算法相比，该方法综合考虑了系统状态噪声和传感器测量噪声，在去除噪声的同时能够更多地保留路面纵断面剖面的细节，获得更精确的去噪结果.

2) 选取AC-13沥青混凝土和SMA-13沥青混凝土2种路面类型作为试验样本，对本文所提改进KF算法与铺砂法和滑动滤波算法进行了试验验证，并建立了2种路面类型的构造深度转换模型.试验结果表明：对于AC-13和SMA-13两种路面类型本文改进KF算法的VMSE值分别为0.001 3和0.002 0，VMAPE值分别为2.29%和3.85%，重复性标准偏差及变异系数均小于5%，与铺砂法相关性系数大于0.95，说明该方法测量精度更高，稳定性更强.

3) 本文仍存在一些不足及局限性，针对我国其他路面类型，如水泥混凝土路面需要进一步进行验证.同时，在采用KF算法进行计算时，系统状态噪声还有待根据实际路面情况进行深入分析，能够更精确地计算出状态预测噪声，从而获得更精确的去噪结果是今后研究中的主要工作.