考虑低周疲劳损伤效应的钢筋混凝土柱Park-Ang损伤修正模型
2020-01-16朱汉波缪长青白六涛邵越风
朱汉波 缪长青 白六涛 邵越风
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(东南大学土木工程学院, 南京 211189)
为了准确评估钢筋混凝土结构震后的损伤程度[1],国内外学者针对混凝土结构构件评估提出了多种损伤模型[2-3].Park-Ang模型[4]是一种用于钢筋混凝土梁柱损伤评估的双参数经典损伤模型,但其存在明显缺陷:构件在单调加载和往复加载作用下存在弹性阶段损伤指标大于0的情况;构件在单调荷载作用下达到破坏状态,损伤指标大于1;未考虑加载路径的影响;未考虑构件随最大位移增加损伤的非线性加速累积现象.针对上述问题,学者们面向不同研究对象提出了多种基于Park-Ang模型的损伤修正模型.文献[5-9]针对损伤指标上下边界问题进行了修正;文献[10]根据Miner准则,考虑加载路径对损伤指标的影响;文献[11]通过多变量非线性回归分析,减小损伤指标离散度.现有修正模型在特定实验中能准确评估构件损伤程度,但是模型的最大变形损伤和滞回耗能损伤部分组合方式仍存在缺陷[12];拟合参数时多采用等幅增量往复加载实验数据,对低周疲劳效应考虑不足.
本文通过调整模型最大变形和滞回耗能效应的组合形式,在滞回耗能损伤中考虑低周疲劳效应的影响,通过遗传算法优化滞回耗能损伤,得到考虑低周疲劳效应的钢筋混凝土构件Park-Ang损伤修正模型.
1 Park-Ang修正模型
针对钢筋混凝土柱的特点,损伤模型的构造规则如下:①构件损伤由最大变形损伤与滞回耗能损伤线性组合而成,弹性范围内损伤为0,完全损伤状态为1.②损伤指标以最大变形损伤为主,滞回耗能损伤为辅,最大变形和滞回耗能效应非线性叠加.其中,最大变形损伤DM随位移增加而非线性累积.③损伤指标中滞回耗能损伤部分包含不同位移幅值和相同位移幅值在任意加载周期的非线性演化规律.
根据规则建立如下新模型:
D=DM+(1-DM)DC
(1)
式中,D为最大变形和滞回耗能效应的非线性组合损伤;DC为滞回耗能损伤;随加载过程中最大位移的增加,DM依照单调加载曲线中相应承载力的大小非线性累积,构造DM函数为
(2)
将式(2)代入式(1)得
(3)
Epl,mo(δM)=Emo(δM)-Eel,mo(δM)
(4)
式中,Emo(δM)、Eel,mo(δM)、Epl,mo(δM)分别表示单调加载位移δM对应的总耗能、弹性耗能和塑性耗能;Eu,mo为单调加载下破坏状态耗能.单调加载荷载-位移曲线与往复加载滞回骨架曲线相比,离散性小,实验模拟难度低,所以选用单调荷载-位移曲线的参量来表示DM.
图1为DM参数示意图.图中,F和δ分别为构件顶点侧向加载的承载力和位移;FM为单调加载位移δM对应的承载力;δM,uld为卸载后残余位移;Fu,mo和δu,mo分别为单调加载破坏点的承载力和位移;Epl,mo(δM)、Eel,mo(δM)和Eu,mo分别为abfa、befb和acda围成的区域面积,都大于0.
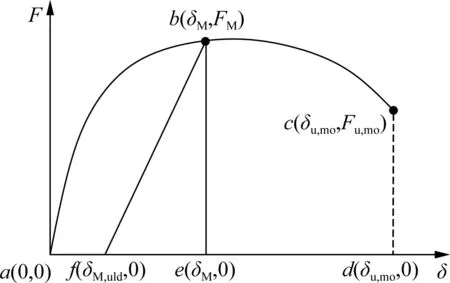
图1 最大变形损伤DM参数示意图
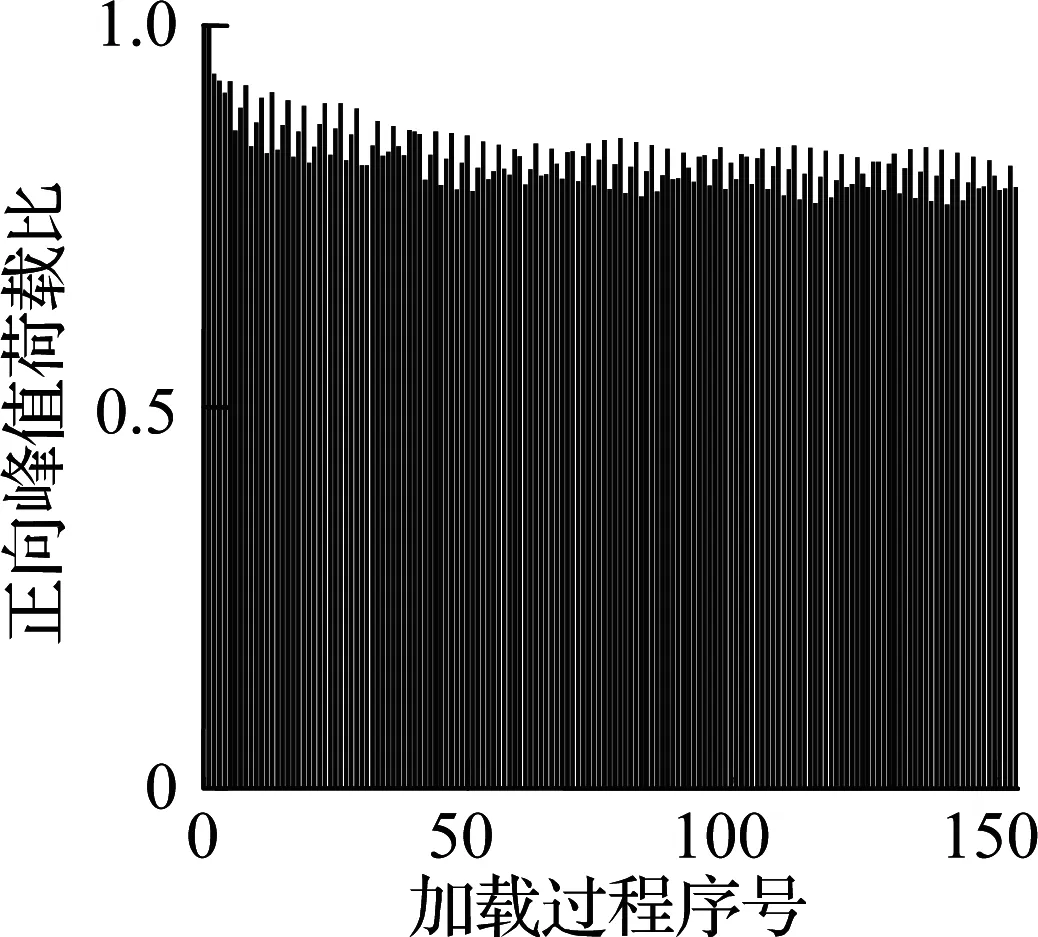
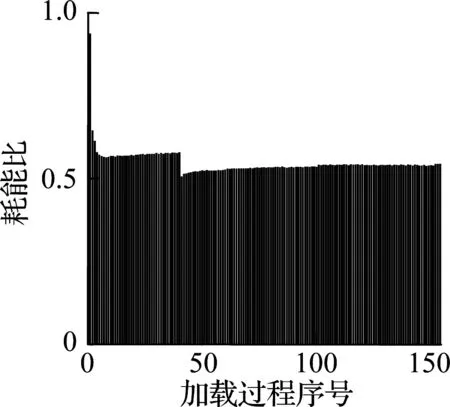
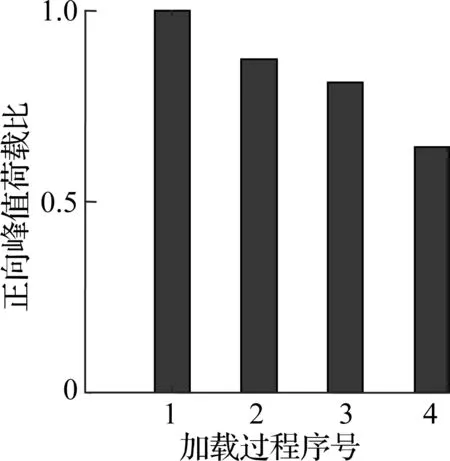
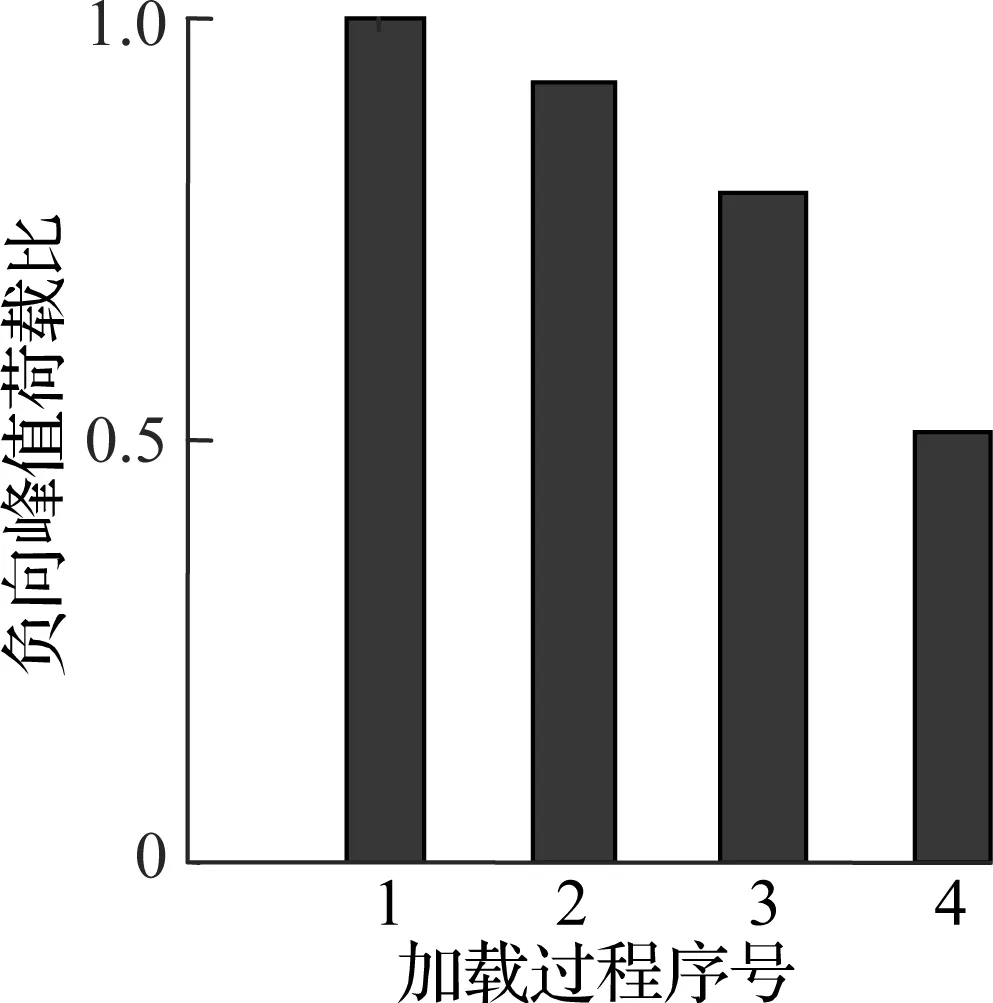
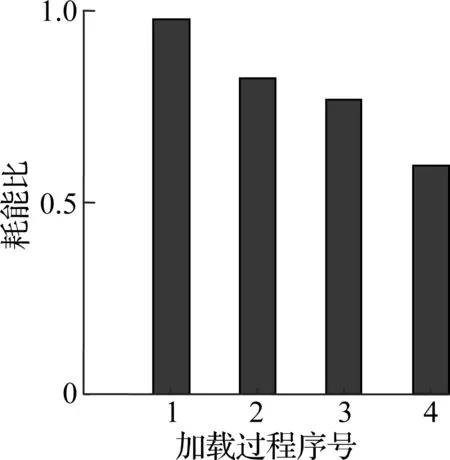
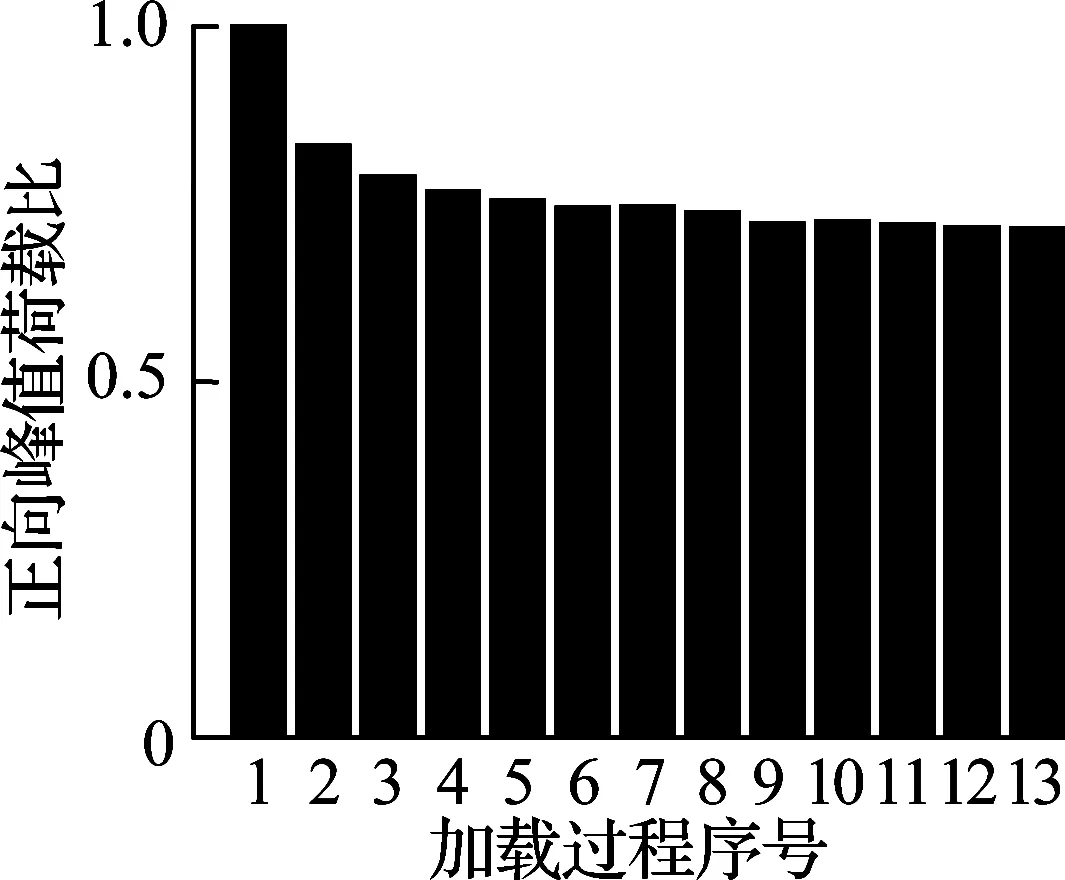
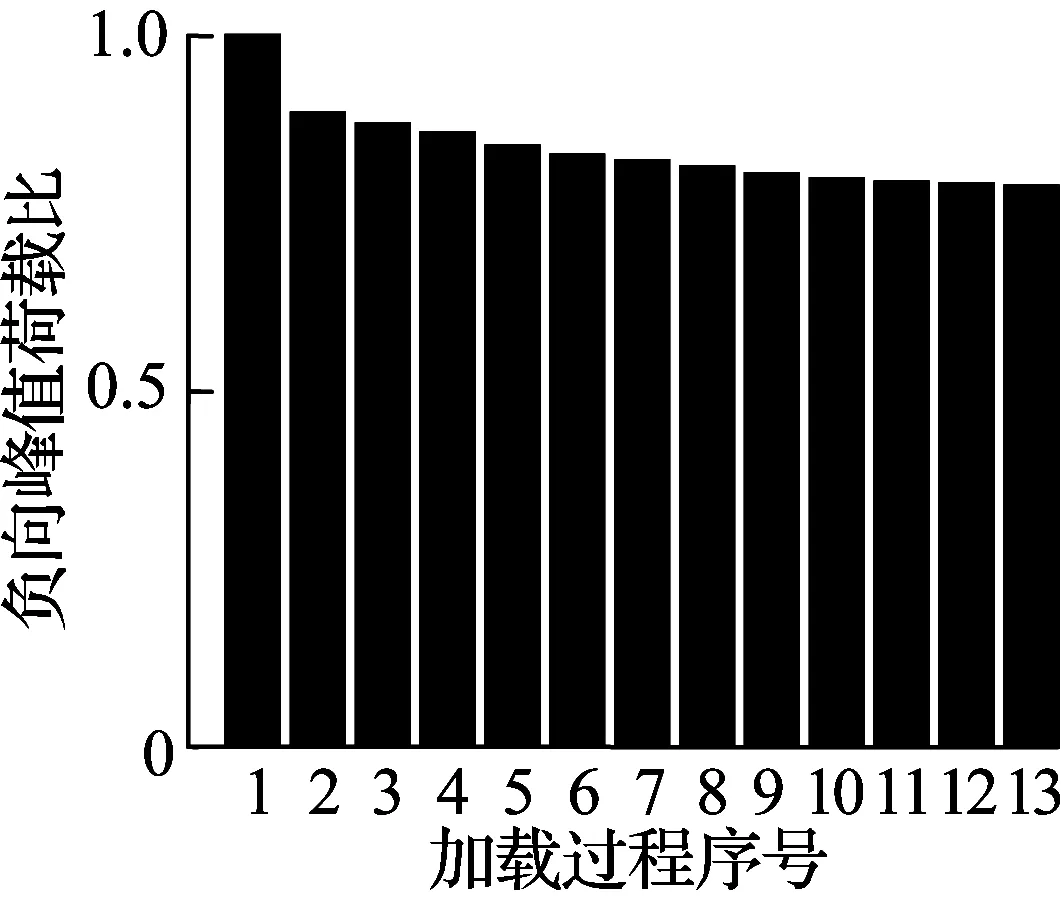
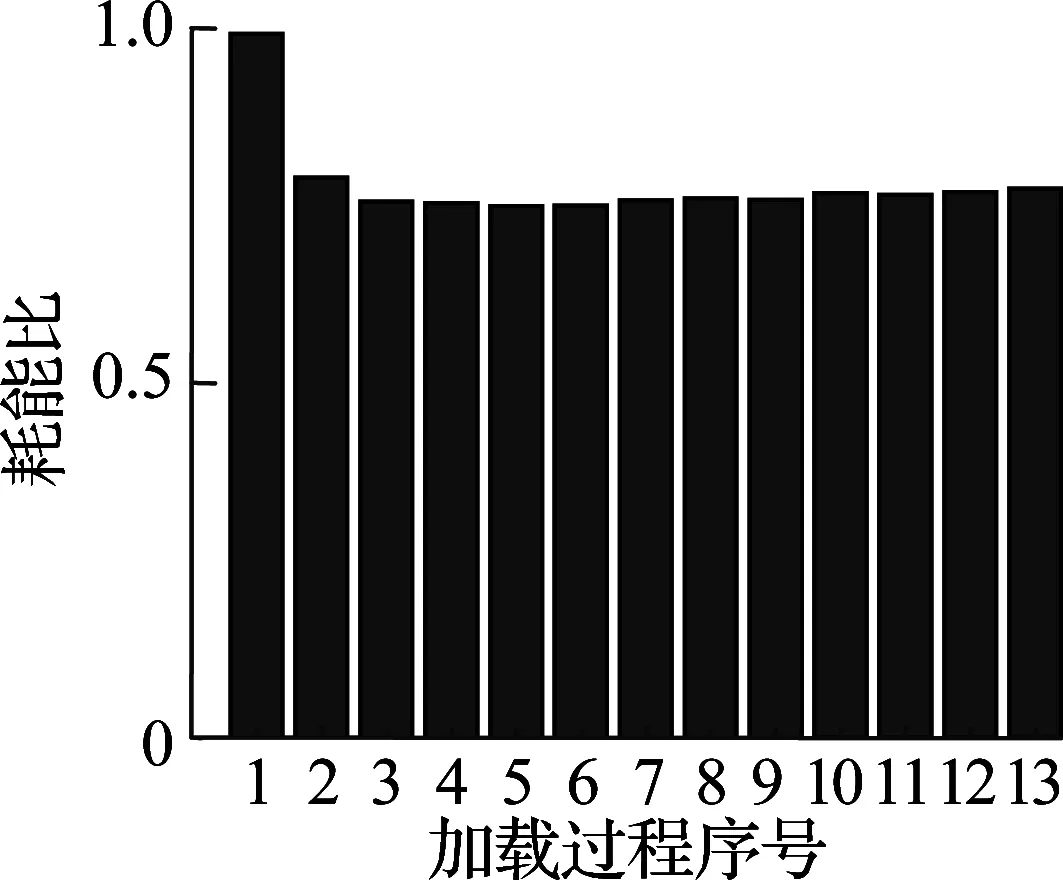
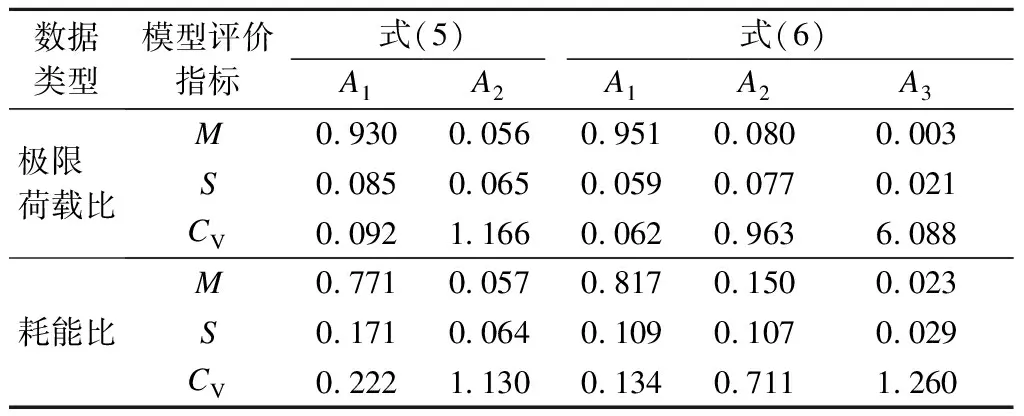
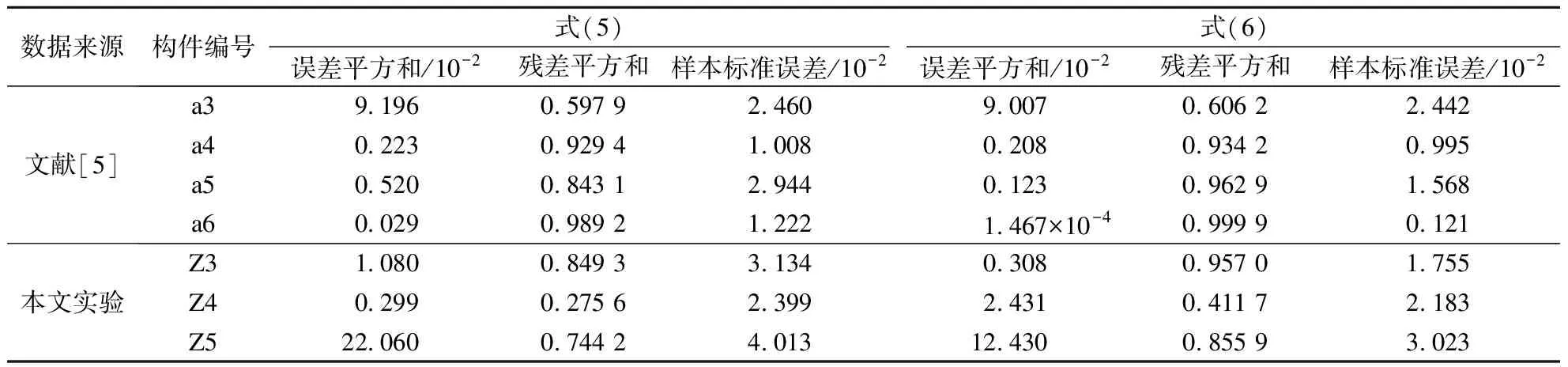
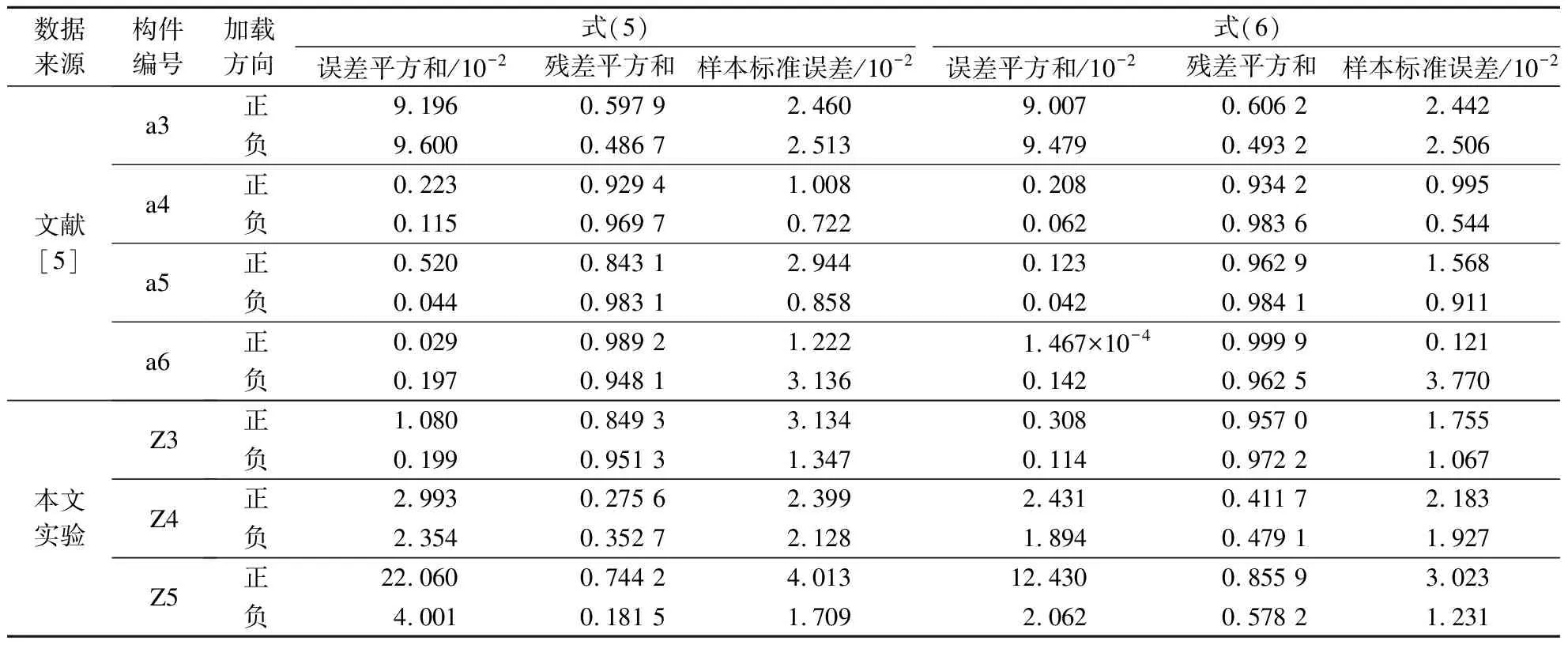
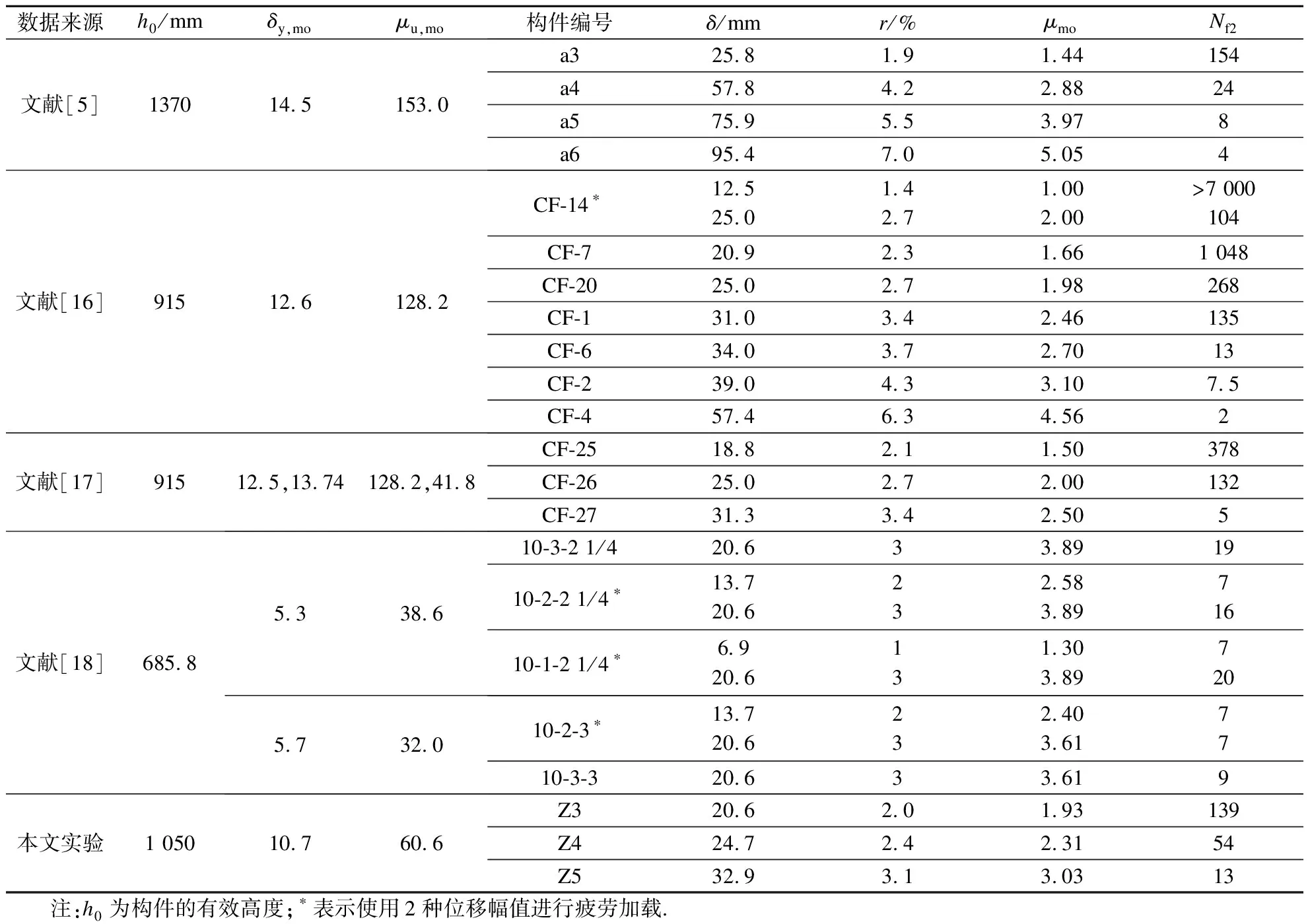
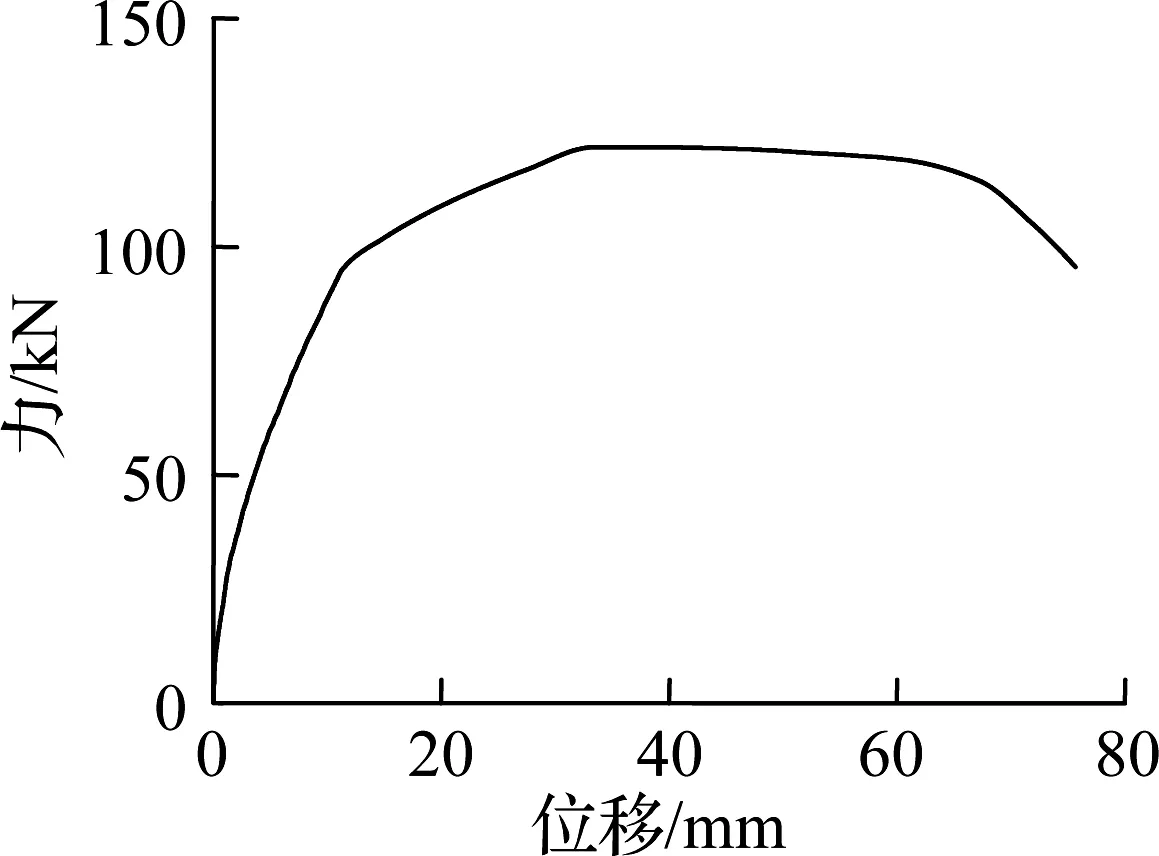
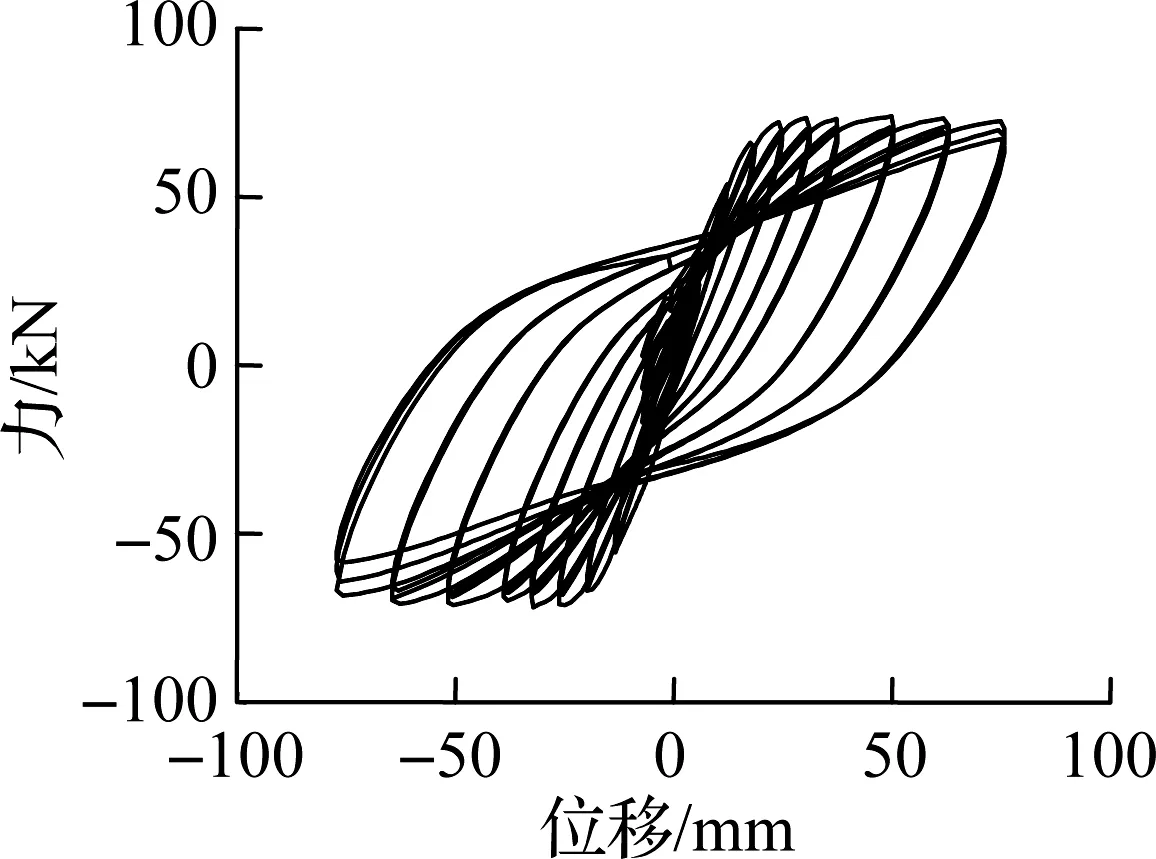
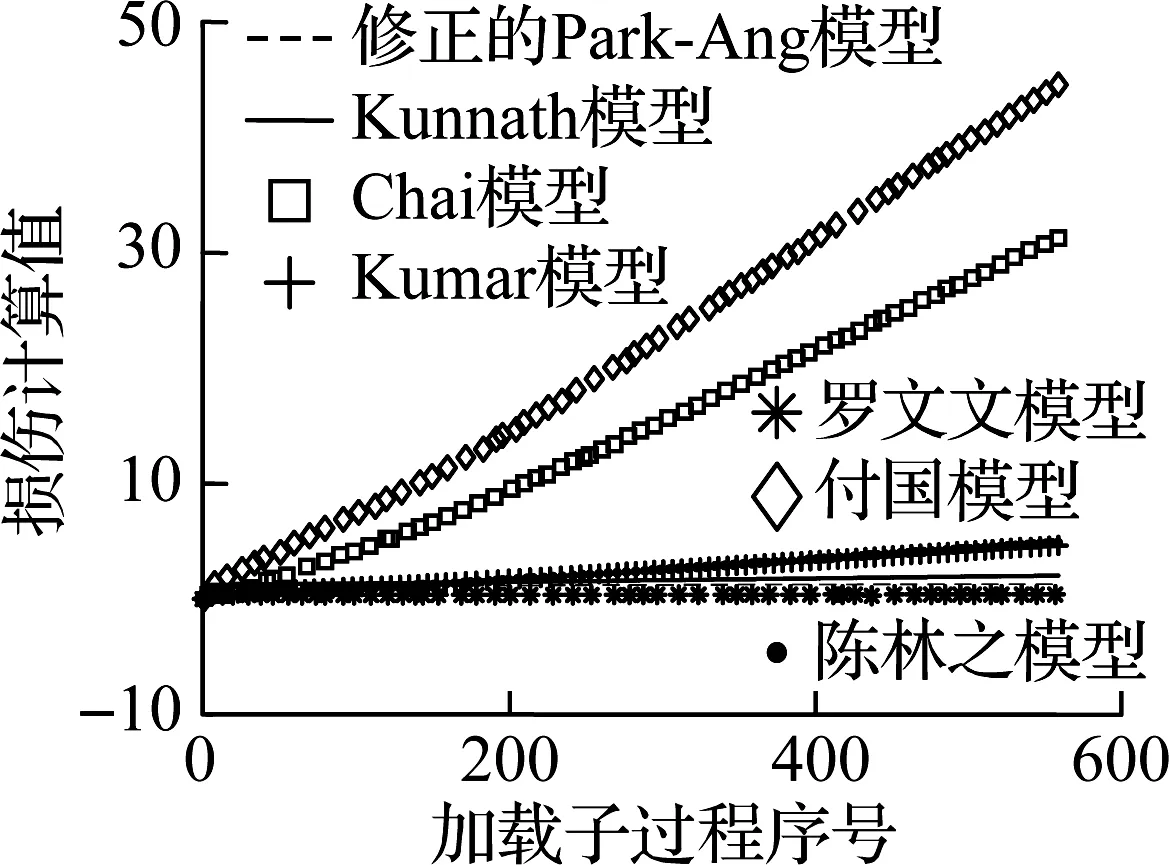
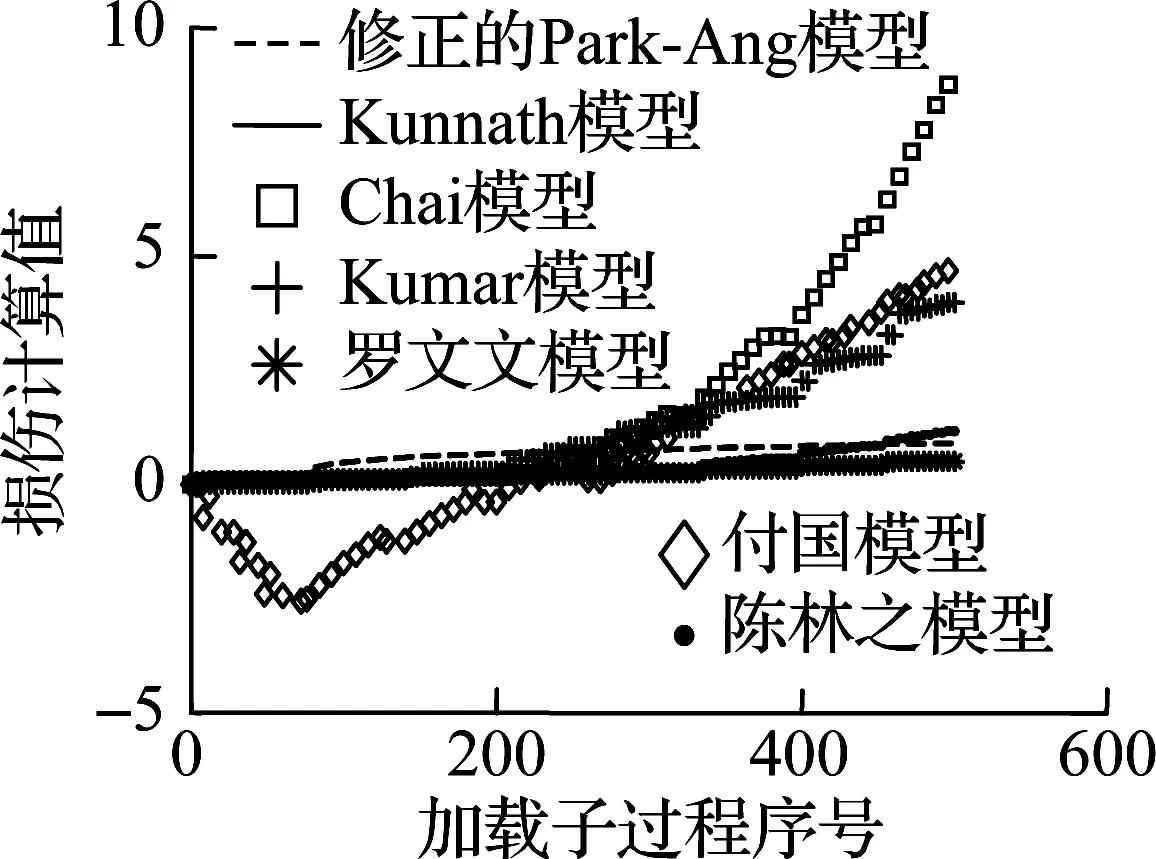
根据文献[13-14]可知,无论剪切破坏柱还是弯曲破坏柱都符合Epl,mo(δM) 对于滞回耗能损伤DC,Jeong等[15]应用Coffin-Manson准则针对钢筋混凝土柱构件提出了非线性滞回耗能表达式.文献[16-18]对基于Miner准则的钢筋混凝土疲劳损伤参数CCM和SCM[10]进行了拟合,对比不同实验的参数拟合结果,SCM差别较小,CCM则差别较大.文献[5,16-18]中参数CCM的计算值分别为4 982、12 000、18 000、268. 现有钢筋混凝土柱低周疲劳实验数据不足,在文献[19]的基础上补充一组构件疲劳损伤实验.以构件Z14作为标准试件,制作5根材料几何参数完全相同的高强钢筋混凝土方形截面柱,实验时按照不同加载路径施加荷载,以研究不同加载路径下的构件强度下降规律.其中,构件Z1为单调加载;构件Z2为增量往复加载;构件Z3、Z4、Z5分别以2.5δy,mo、3δy,mo、4δy,mo等幅往复加载. 文献[16-18]中的滞回耗能损伤模型对位移加载路径考虑不足,针对这一问题收集钢筋混凝土柱疲劳实验数据.所收集的数据包括2类:①文献[5]和本文实验中包含完整的顶点力-位移数据,但构件数少;②文献[16-18]中的实验数据,虽然只提供了骨架或单调加载曲线和特征点数据,但构件数较多.采用这2类数据分别构造DC,引入破坏临界状态反算出疲劳寿命,拟合模型参数.通过对比2类模型的疲劳寿命计算和实验值,选出最优模型. 根据构件Z3、Z4、Z5和文献[5]中构件a3、a4、a5、a6共7组钢筋混凝土柱低周等幅往复加载实验的顶点力-位移数据,引入无量纲变量峰值荷载比和耗能比,分析耗能退化和强度退化规律.对比2组数据,选择更能反映疲劳损伤演化规律的一组数据进行疲劳参数拟合,用形如y=f(A1,A2,…,Ai,…,An,n)的非线性公式,描述相同加载幅值下,不同周期的损伤累积增速减缓现象.其中,n表示自变量循环周期;y表示因变量峰值荷载比(RL)或耗能比(RE);A1,A2,…,Ai,…,An表示模型拟合参数.用形如A1=f(R),A2=f(R),…,Ai=f(R),…,An=f(R)的非线性公式,描述构件在不同加载位移幅值下损伤程度随位移幅值非线性加速累积现象,其中塑性变形延性系数R=(μmo-1)/(μu,mo-1),μmo、μu,mo、δy,mo分别为单调加载下的位移延性比、极限位移延性比和侧向顶点屈服位移.引入损伤边界条件,修正疲劳损伤累积函数得到DC. 考虑弯剪受力柱的破坏规律,参考文献[19],以承载力从平稳下降变为突降和构件承载力下降80%作为构件失效标准,对2组构件承载力退化和耗能退化规律进行分析.选用文献[5]中构件a3、a6和本文实验中构件Z3为例,说明构件循环退化规律.构件在位移等幅加载下的实验数据如图2所示. 对比文献[5]中构件a3和a6的实验结果可知,等幅加载实验中RL和RE随位移幅值增加而加速下降.对比构件Z3的实验结果可知,RL和RE随循环周期增加而降幅减缓.根据RL、RE与耗能损伤之间存在的负相关关系可知,随周期增加损伤累积增速减缓. (a) 构件a3的正向峰值荷载比 (b) 构件a3的负向峰值荷载比 (c) 构件a3的耗能比 (d) 构件a6的正向峰值荷载比 (e) 构件a6的负向峰值荷载比 (f) 构件a6的耗能比 (g) 构件Z3的正向峰值荷载比 (h) 构件Z3的负向峰值荷载比 (i) 构件Z3的耗能比 对比7个构件21组数据,其中RL包含14组数据,RE包含7组数据.为避免人为构造拟合函数在形式上不合理的缺陷,使用基于遗传算法[20]的符号回归程序Eureqa[21]自动搜索n与RL或RE的函数关系.符号回归[22]的终结符集合主要由随机量和变量以及运算符组成.为兼顾搜索运算的效率和有效性,定义初始函数集为基本数学运算符、三角函数和指数对数运算符.为避免过拟合的情况,拟合函数时,按RL或RE数据相对大小加权,将函数映射关系的平滑度调整到60%.设定目标表达式为RL=f(n)或RE=f(n),适应度评价采用原始适用度指标平均绝对误差EMA,其值越大则适应度越差,淘汰EMA>0.2的个体.不设置种群大小和最大遗传代数限值,仅将EMA<0.01作为程序终止运行标准.运行程序后得到2组符合规律的疲劳退化模型,即 y=A1-A2log(n) (5) y=A1-A2log(n)+A3n (6) 式中,A1为常参数;A2为自然对数参数;A3为一次项参数. 式(5)和(6)的参数及其拟合度指标对比结果见表1.基于RL和RE,分别拟合出2组参数的平均值(M),得到共计4组拟合参数.比较标准差(S)和变异系数(CV)发现,基于RL数据的标准差和变异系数更小,说明基于RL数据的公式拟合度更高.与式(5)相比,式(6)中参数A1和A2的标准差和变异系数更相近;但式(5)中参数A3的变异系数大,导致A3的平均值无法代表其实际取值.模型函数拟合度指标见表2和表3.由表可知,各构件峰值荷载退化和耗能性能退化实验值与式(5)和(6)的计算值误差平方和均小于0.15,样本标准误差均小于0.04,残差平方和均值也超过0.7,说明这2种模型都满足函数拟合精度要求. 表1 模型参数拟合度对比 表2 RL参数拟合度指标 表3 RE参数拟合度指标 由上述分析可知,RL比RE更能反映疲劳退化规律,式(5)和(6)的拟合度相当.考虑到式(6)中参数A3因离散度大而无法确定,本文选用式(5)来拟合RL数据,确定疲劳退化参数A1和A2,得到非线性等幅加载疲劳退化函数. 考虑不同位移加载幅值对疲劳退化规律的影响,对数据1中的14组RL数据进行进一步处理发现,加载幅值参数δy,mo、μu,mo、R与参数A1、A2存在较大相关性.因此,在A1=f(δy,mo,μu,mo,R)和A2=f(δy,mo,μu,mo,R)的函数框架下,使用遗传算法分别搜索出2组拟合度超过90%的函数表达式,A1的2组表达式记作A11和A12,即 A11=0.946+0.089R (7) A12=0.957+0.124R2 (8) A2的2组表达式记作A21和A22,即 A21=0.069 1+0.087 3R2-0.344R (9) A22=0.046 7+R4 (10) 式(7)~(10)中只包含变量R,说明参数A1、A2与δy,mo、μu,mo相关性低.将A1、A2参数表达式组合,得到(A11,A21)、(A11,A22)、(A12,A21)、(A12,A22)四个参数组,代入式(5). (A12,A21)的参数组计算值更接近实验值.令A1=A12,A2=A21,等幅加载下的峰值荷载比为 μFec=A12-A21lg(n) (11) 令n=0.5表示单调加载工况,根据结构破坏的边界条件可得 μFec=A12-A21lg(n+A4) (12) 当n=0.5时,R=1,参数A4的平均值为1.598. 用极限荷载比来表示损伤程度,循环加载骨架曲线的峰值在最初加载过程中达到最大值,DC=0;峰值随循环数增加逐渐降低,损伤逐渐累积,最终破坏,DC达到1.令Dec为等幅循环加载累积损伤,其计算公式为 (13) 式中,Fec、Fp,ec、Fu,ec分别为等幅循环加载下的承载力、峰值承载力和极限承载力. 对式(13)进行归一化处理,引入循环加载下的峰值荷载比μFec=Fecy/Fp,ecy,塑性极限荷载比μFec,u=Fu,ec/Fp,ec,则 (14) 将式(12)代入式(14),根据文献[19],μFec,u=80%,由R便可计算得到Dec. 钢筋混凝土构件截面形式、尺寸、剪跨比、轴压比、纵筋配筋率和配箍率的改变会引起μu,mo、δy,mo、R变化.同时,这3个参数又与Nf2紧密相关,随μu,mo的增加,Nf2增加;随μmo=δmo/δy,mo增加,Nf2下降.根据文献[5,16-18]中钢筋混凝土柱低周等幅往复加载实验顶点力-位移数据,建立μu,mo、δy,mo、R与Nf2的函数关系式. 表4给出了构件的无量纲特征值和寿命实验值.设定3种疲劳寿命预测模型的目标表达式分别为Nf2=f(r,ry,mo,ru,mo),Nf2=f(μ,μu,mo),Nf2=f(R),其中r=δ/h0为等幅加载位移角,ry,mo=δy,mo/h0为单调加载屈服位移角,ru,mo=δu,mo/h0为单调加载极限位移角. 基于遗传算法的自动搜索方法,拟合无量纲数据,考虑欠拟合和过拟合的情况,沿用2.1节的初始函数集、程序终止运行标准和适用度指标等参数设定,运行程序得到符合条件的函数.在此基础上,按照复杂程度低于15、参数个数小于等于3、拟合误差低于0.2的原则,初步选择拟合函数,并给出参数取值(见表5).表中包含14组函数,符合条件的函数较多,因此将拟合误差的选择标准降低到0.1,并引入拟合优度、拟合度和最大误差等多个拟合度评价指标对比复选出拟合函数.疲劳寿命函数复选结果见表6. Nf21=1.756+2 665e-465.6R+0.5 (15) Nf22=2 656e-443.3R-1.256 (16) 将2.1节中的(A11,A21)、(A11,A22)、(A21,A21)、(A21,A22)代入式(5)的(A1,A2)中,结合破坏状态和单调加载边界条件,得到4组基于数据1的疲劳寿命计算模型Nf1和基于数据2的2组疲劳寿命计算模型Nf2.使用6组模型计算疲劳寿命与实验结果Nft进行对比,结果见表7.根据Nft对6组疲劳寿命计算值进行归一化处理,得到归一化数据的平均相对误差值.Nf13的归一化平均相对误差为0.16,远小于其他模型,故用其进行寿命计算,并将Nf13给出的参数组合代入式(11)~(14),计算等幅加载钢筋混凝土构件的滞回耗能损伤DC. 表4 构件实验无量纲特征值 表5 疲劳寿命函数拟合初选结果 表6 复选疲劳寿命函数的拟合度指标 表7 循环寿命计算值和实验值对比表 在地震荷载下,结构中的钢筋混凝土柱加载路径各异.本文将等幅加载工况下的滞回耗能损伤模型推广到任意加载工况.在任意加载过程中,将一个加卸载连续过程作为一个加载子过程,对于等幅加载实验而言,半个加载循环为一个加载子过程.将整个加载工况划分为nh个子过程,式(12)中n=nh/2.将式(8)和(10)代入式(12),得 μFec=0.957+0.124R2-(0.069 1+0.873R2- (17) 对于相同构件2种不同位移幅值的等幅疲劳加载实验,可将R分别记作RN和RM,且RN≠RM.若构件分别在第nh,i和nh,j次加载过程中达到相同的损伤状态,根据式(12),建立方程μ(RN,nh,i)=μ(RM,nh,j),化简得到nh,j=f(RN,nh,i,RM),则 (18) 式(18)可以换算在相同μFec和不同R下的半循环加载过程数nh.假设整个加载过程包含Q个子过程,每个子过程的R记作R1,R2,R3,…,Rk,…,RQ,其中Rk表示第k个加载子过程的塑性变形延性系数.将k个加载子过程后的损伤DC,k代入式(14),反算出k个加载子过程后的峰值荷载比μFec,k,再将Rk代入式(17),换算出以Rk为加载特征的等幅循环加载半循环次数nh,k.令RN=Rk,RM=Rk+1,nh,i=nh,k,已知k+1个子过程后的等幅半循环次数nh,k+1=f(Rk,nh,k,Rk+1)+1,代入式(18)有 (19) 将R=Rk+1,n=nh,k+1代入式(17),计算得k+1个子过程后的极限荷载比值为 (20) 令μF,u为塑形荷载比,当μF,k+1<μF,u时,表示k+1个加载子过程后构件破坏;反之,构件未破坏,进入下一个加载子过程,直到μF,k+1>μF,u,停止计算. 结合式(18)和(19),将式(14)中的Dec推广到任意加载过程累积损伤DC的计算公式中,则DC,k的表达式为 (21) 已知μF,u=80%,k个加载子过程后的极限荷载比为μF,k,根据式(21)可计算得到累积损伤DC,k.利用MATLAB软件编写程序,已知任意加载过程的顶点力-位移曲线,便可计算出整个加载过程中构件的损伤演化规律. 以单调加载、等幅增量加载和等幅往复加载为对比案例,将构件Z1、a2和Z5的整个加载过程按照顶点力-位移曲线中位移单调性和力正负值变化划分成多个加载子过程,分别用Kunnath模型[5]、Chai模型[6]、Kumar模型[7]、罗文文模型[10]、付国模型[9]和陈林之模型[8]及修正的Park-Ang模型进行疲劳损伤演化计算,结果见图3.构件加载到破坏状态的损伤计算值见表8. (a) 构件Z1的顶点力-位移曲线 (b) 构件a2的顶点力-位移曲线 (c) 构件Z5的顶点力-位移曲线 (d) 构件a2的损伤对比 (e) 构件Z5的损伤对比 表8 各损伤模型在破坏状态下的损伤计算值 以构件Z1为例,验算单调加载过程中各损伤模型的计算结果.对比表8中各模型最终损伤状态模型计算值可知,除付国模型计算出的破坏状态损伤数值大于1外,其余损伤模型得到的计算值都接近1.对于单调加载构件而言,Chai模型、罗文文模型和修正的Park-Ang模型在计算单调加载构件的损伤值时最为准确,其次为Kunnath模型、Kumar模型和陈林之模型,付国模型的计算值误差最大. 以构件a2为例,验算增量往复加载子过程中各损伤模型的计算结果,实验中构件一共经历125个加载子过程.如图3(d)和表8所示,在第0~60个加载子过程中,付国模型的损伤计算值小于0,不符合客观规律.Kumar 模型、付国模型和Chai模型分别在第70、78、72加载子过程后损伤计算值达到1,最终破坏状态的损伤计算值分别为3.986、4.671、8.706,远大于1,评估结果过大.Kunnath模型和罗文文模型在破坏状态的损伤计算值为0.477和0.506,远小于1,评估结果过小.陈林之模型和修正的Park-Ang模型计算所得的破坏状态损伤值为1.169和0.901,接近于1,误差可以接受,其中修正的Park-Ang模型相对更为精确.对于等幅增量往复加载构件而言,陈林之模型和修正的Park-Ang模型可以准确地反映构件的损伤演化过程,其余模型损伤计算误差较大. 以构件Z5为例,验算在增量往复加载过程中各损伤模型的计算结果,实验中构件一共经历559个加载子过程.如图3(e)和表8所示,Chai模型、Kumar模型、付国模型和陈林之模型分别在第30、96、6、112个加载子过程后损伤计算值达到1,在破坏状态的损伤计算值为31.270、4.638、44.547、4.885,远大于1,评估结果过大.罗文文模型在最终损伤状态损伤计算值为0.402,远小于1,评估结果过小.Kunnath模型和修正的Park-Ang模型在破坏状态的损伤计算值为1.014和1.007,接近于1,误差可以接受,其中修正的Park-Ang模型相对更为精确.对于等幅往复加载构件而言,修正的Park-Ang模型和Kunnath模型的损伤计算误差小于10%,可以准确地反映构件的损伤演化过程,其余模型损伤计算误差均大于10%. 综上所述,多种荷载加载方式下,钢筋混凝土的损伤模型有效性见表9.由表可知,只有修正Park-Ang模型适用于评估钢筋混凝土构件在不同加载路径下的损伤演化规律. 表9 钢筋混凝土的损伤模型有效性 1) 针对已有钢筋混凝土柱评估损伤模型的缺陷,按照非线性叠加规律,调整模型最大变形和滞回耗能效应的组合形式,在滞回耗能损伤中考虑低周疲劳效应的影响,给出了修正的Park-Ang模型. 2) 以钢筋混凝土柱为研究对象,按照不同位移幅值及相同位移幅值下不同加载周期的非线性演化规律,给出初始函数集、目标表达式、适用度指标和程序终止运行标准的设定范例,使用遗传算法的符号回归程序确定DC的最优函数. 3) 对比Kunnath模型、Chai模型、Kumar模型、罗文文模型、付国模型、陈林之模型和修正的Park-Ang模型,验证了本文模型的适用性和准确性. 4) 采用MATLAB编程,实现了从滞回曲线输入到多种损伤模型结果自动输出,为以后补充实验数据、优化模型参数提供便利.2 滞回耗能损伤
2.1 滞回耗能损伤模型

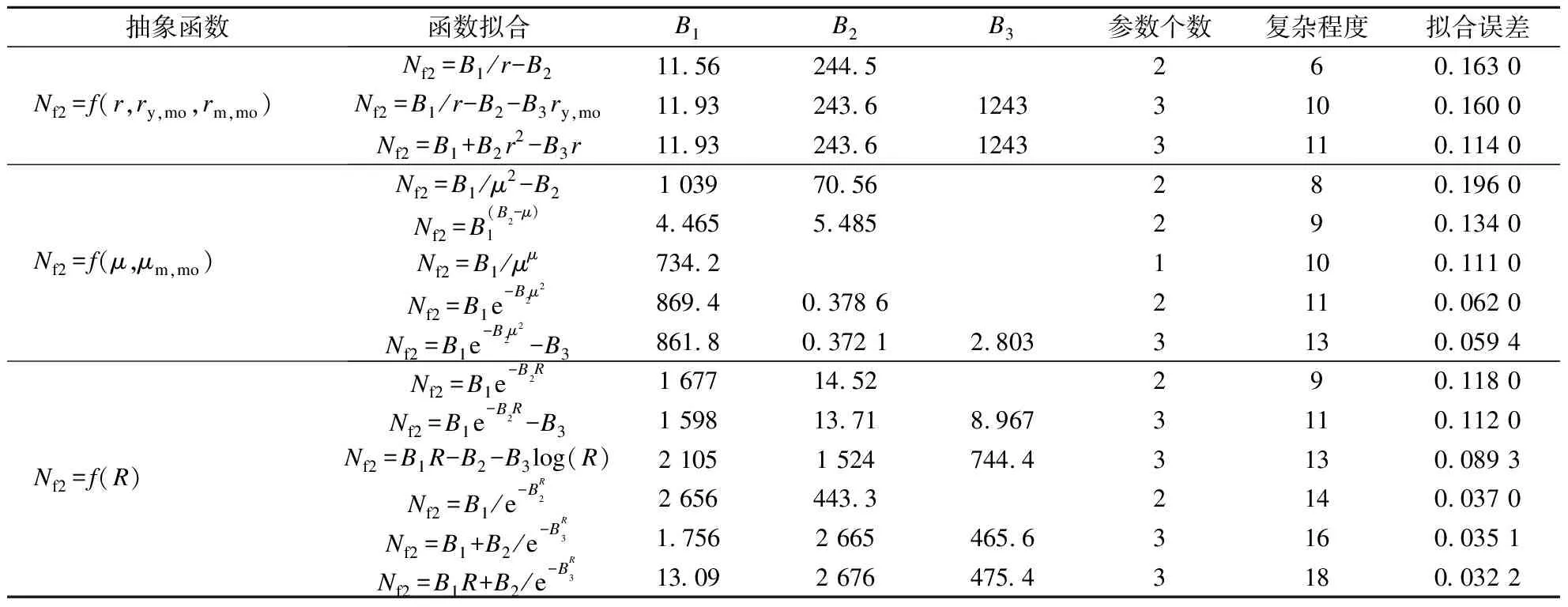
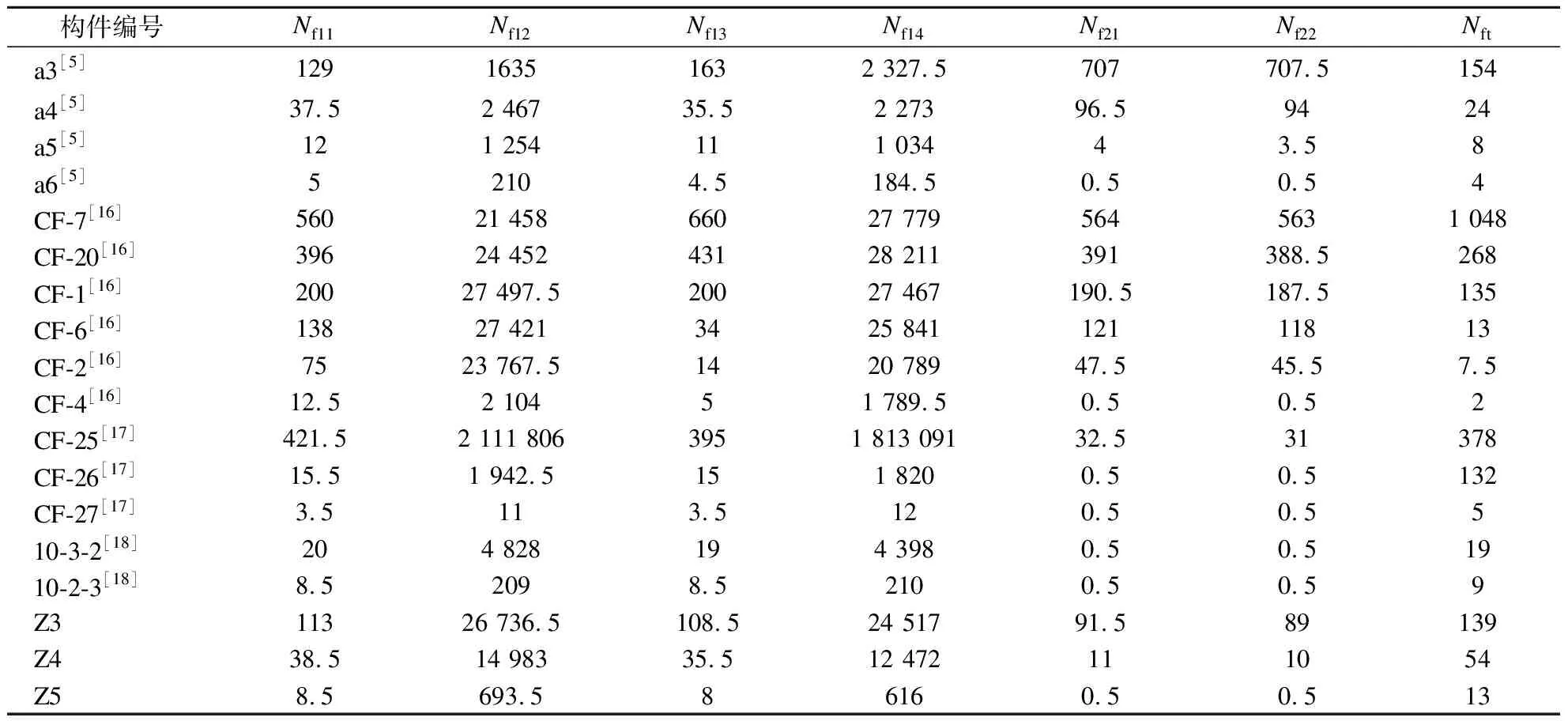
2.2 疲劳寿命
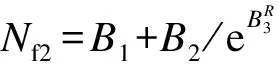

2.3 任意加载路径下的累积损伤
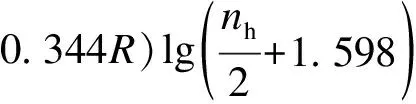
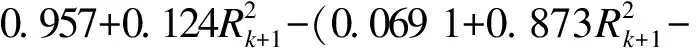
3 损伤模型对比



4 结论
