自下而上的群体居民日负荷预测
2020-01-16朱云毓高丙团朱振宇刘晓峰秦艳辉
朱云毓 高丙团 陈 宁 朱振宇 刘晓峰 秦艳辉,3
(1东南大学电气工程学院, 南京 210096)(2中国电力科学研究院有限公司新能源与储能运行控制国家重点实验室, 南京 210003)(3国网新疆电力有限公司电力科学研究院, 乌鲁木齐 830011)
随着智能电网的发展,电力市场自由贸易与电力行业分拆机制不断完善,智能电表、智能家电及能量管理系统逐步得到普及应用[1-3].在智能电网的环境下,需求响应借助智能终端的决策与控制,能够更好地实现对用户用电行为的管理和调控;同时借助信息交互技术优化用户的用电行为,提升电力市场的效率[4].由于居民用户是需求侧的重要组成部分,因此智能需求响应需要将其行为及态势作为依据,制定合理的价格信号或激励机制以引导居民用户群体的用电行为,从而响应电力系统的调度[5].为了能够准确分析居民用户需求响应趋势、研究居民用户的用电行为,准确预测居民群体用户的日负荷情况尤为关键[6].
居民负荷的建模方法主要分为2类:自上而下的负荷建模和自下而上的负荷建模[7].前者的建模思想是从终端负荷出发,基于测量数据归纳出整体负荷特性;后者是从个别家庭的家用电器负荷模型出发,层层叠加构成整体负荷模型.自下而上的建模方法需要的数据量庞大,但是该方法精度高,能够得到各层的负荷数据,且可以分析单户家庭的用电行为对整体负荷的影响.文献[8]基于用户历史用电行为,引入概率函数及马尔科夫链蒙特卡洛算法,建立居民负荷模型并绘制家庭日负荷曲线,并通过对比预测功率和实际功率的相对误差进行验证.文献[9]基于智能电表采集的各电器历史数据,同时考虑了电器开关状态及房间数量,采用自下而上的建模方法建立了一幢楼宇的日负荷模型.文献[10]基于心理学模型,通过负荷曲线的叠加将负荷模型由个人用电行为外推至群体用电行为.
合理地选择预测相似日是提升预测模型精准度的有效途径.文献[11]通过事件记录获取各电器的用电时长及用电次数,采用自下而上的模型建立了用户负荷单元,实现需求侧管理.文献[12]在建立相似日的基础上,采用自下而上的建模方法对居民日负荷进行预测.文献[13]在考虑社会活动因素前提下选取相似日,建立了基于气象因素的短期负荷预测灰色模型.
上述建模主要有以下2个问题:
1) 在考虑外界因素如气象、日期等因素对用户用电行为的影响时,只有部分因素被纳入模型,不够全面.
2) 采用自下而上的建模方法建立群体用户负荷模型时,只是单纯地叠加单个用户负荷曲线,或者未将电器功率、家用电器组合情况等随机因素纳入模型.
针对上述问题,本文在建立单户家庭用电行为模型的基础上,采取自下而上的分析模式研究群体居民用户用电行为模型的建立方法.考虑到群体用户具有家用电器种类差异、家用电器功率差异、用电行为不统一等特点,本文将以数据预处理和聚类分析后所选取不同类型群体用户中的典型家庭为基础,结合中心极限定理和蒙特卡洛方法对家用电器组合、家用电器功率组合及用电行为时间分布进行模拟,并利用MATLAB软件对小区的居民用电数据进行分析以验证所提预测方法的适用性和准确性.
1 用户日负荷预测框架
本文所提的居民用户日负荷预测方法基于自下而上的建模思想,将预测模型分为4个模块,分别是聚类分析模块、相似日提取模块、用户用电行为分析模块及用户负荷预测模块.
首先,聚类分析模块通过分析家庭用电特征历史数据,对群体用户进行聚类分析,筛选出每一类别中的典型家庭,典型家庭必须满足下列2个条件:① 该家庭的日负荷接近于该类居民用户平均日用电量;② 该家庭的日负荷包含所有待统计的典型家用电器.其次,相似日提取模块通过分析环境温度、空气相对湿度等数据,选取与预测日相似度最高的历史日.接着,用户用电行为分析模块基于典型家庭各家用电器在相似日的历史开关状态形成电器行为模型,得到各家用电器在预测日的开关概率,从而获得各类型典型家庭的日负荷期望.最后,用户负荷预测模块分为2个层面,一个是利用蒙特卡洛方法,对家用电器的拥有率和家用电器的功率分布进行模拟;另一个是根据获得的典型家庭的用电行为概率,对典型用电行为时间点进行蒙特卡洛随机抽样.将家用电器拥有率、家用电器功率及用电时间点的差异性纳入群体居民负荷模型,从而得到各类别的用户负荷期望,进而获得群体用户总的负荷期望.
2 单户居民用电行为模型
影响居民用电行为的因素众多,主要可归纳为外界环境因素和自身条件因素.本节的相似日选取将这2类因素同时纳入模型,实现对单户居民的用电行为分析.
2.1 相似日选取
本文基于历史日对居民用电行为进行建模,因此合适的历史样本可以较为准确地模拟预测当日外界因素对家庭用电行为的影响[14].负荷预测精度主要受天气情况、日期类型、社会事件等因素影响.基于此,本文考虑的因素如下:人体舒适度、日期差距、星期类型、重大事件、PM2.5和日最高气温.皮尔逊相关系数是用来度量2个随机变量之间线性相关程度的重要指标,上述因素与负荷对应的皮尔逊相关系数分别为0.696、-0.530、0.430、0.406、0.124和0.113.本文利用皮尔逊相关系数选择了相关性绝对值大于0.400的特征因素[15],将人体舒适度因子、日期差距因子、星期类型因子和重大事件因子纳入单户居民的相似日特征向量,并采用相似度特征向量表征历史日与预测日的相似程度.设定多个单户居民相似度特征矩阵X如下:
X=[α,δ,λ,θ]
(1)
式中,α为人体舒适度因子;δ为日期差距因子;λ为星期类型因子;θ为重大事件因子.
1) 人体舒适度因子
相较于风寒指数、炎热指数等独立的指标,人体舒适度因子能够更加综合地反映气象条件与负荷之间的关联.因此采用人体舒适度因子来衡量预测日与历史日在气象上的相似程度[16-17],则预测日与历史日相似度的日期差距因子αh的计算公式如下:
αh=1.8Ta-0.55(1.8Ta-26)(1-Hr)+
(2)
式中,Ta为环境温度,℃;Hr为空气相对湿度;u为平均风速,m/s.
2) 日期差距因子
随着经济发展,居民负荷呈周期性上升.因此,选取的相似日与预测日越接近,其负荷特征越有参考价值.采用日期差距因子来表示预测日与历史日在长期时间跨度上的相似程度,且相似度随预测日与历史日的绝对时间差增大而减弱[13],则预测日与历史日相似度的日期差距因子δh的计算公式如下:
(3)
3) 星期类型因子
从短期来看,居民负荷在一个星期内的各天也呈现出一定的规律性[18].因此,采用星期类型因子衡量预测日和历史日在星期类型上的相似程度,星期类型相似程度越大,该因子的数值越大.为了区别工作日和休息日,将星期类型映射到[0.1,1]的区间内,以体现星期类型的影响.
预测日与历史日相似度的星期类型因子λh的计算公式如下:
λh=1-|f(Ch)-f(Cp)|
(4)
(5)
式中,Ch、Cp分别为历史日和预测日的星期类型;w=1、2、3、4、5、6、7分别表示星期一至星期日;f(Ch)为Ch映射后的值.
4) 重大事件因子
由于某些重大事件的影响,居民的用电行为会出现短时间的波动,本文主要考虑春节等重大节假日对居民用电行为的影响.因此,必须将重大事件因子纳入相似度特征向量以考虑其对居民用电行为的影响.预测日与历史日相似度的日期差距因子θh的取值如下:
(6)
式中,dh、dp分别表示历史日和预测日,当dh与dp为同一节假日时,θh=1;否则θh=0.其中,不同的重大事件类型以(0,1)之间的不同数值表示.
相似度特征向量中4个因子的计算结果在数量级上存在较大的差异,将导致各因子所占的权重存在较大差异,从而使个别因子起决定性的作用而某些因子被忽视,因此,需要对相似度特征向量中各因子进行归一化处理.本文采用极值归一化对数据进行处理,即
(7)
式中,α′、δ′、λ′、θ′为经过归一化处理后数量级相同的各特征因子分别组成的向量;αj、δj、λj、θj为未经归一化处理的各特征因子向量α、δ、λ、θ中的分量值.
相似度特征向量中4个因子重要程度可能有所不同,灰色关联度分析法是一种多因素分析方法,可利用上述4个特征因素构造特征序列,计算该特征序列与家庭总负荷序列发展趋势的相似或相异程度[17],从而判断该特征因素与负荷的关联程度,并将其用于确定特征因素的权重.关联度越大,说明该因素在整个体系中的重要程度越大,权重也越大.
采用加权欧几里得距离法对各归一化后的相似度特征向量进行距离衡量[19],即
(8)
式中,xh、xp分别表示历史日和预测日归一化后的相似度特征向量,l(xh,xp)为xh、xp两个向量之间的加权欧几里得距离;xh,k为第k个历史日的相似度特征向量;m为筛选出相似度因子最高的历史日个数,1≤k≤m;ωr为第r个特征因子的权重;v为特征因子的个数,1≤r≤v.相似度特征向量间的距离越小,其相似度越大,相似度因子s可表示为
(9)
2.2 居民负荷开关模型
对于单个家庭的第k个历史相似日,k∈{1,2,…,m},数据库中共记录有该家庭的I个家用电器的开关情况,若记录时间间隔为tg,则对于每个家用电器i,i∈{1,2,…,I},当天会有J=(24×60)/tg个记录点,tg为1 440的因数.
通过智能电表借由智能插座采集各设备的耗能情况、运行特性,智能插座能够反馈出插座里的电子设施的电量、功率、电压等数据.将某一设备在采样时刻获得的功率与其待机功率作比较,可以获得其开关状态,即
(10)
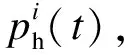
(11)
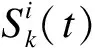
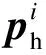
(12)
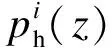
在此基础上可以建立起单个家用电器的日负荷模型,即
(13)
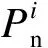
单户家庭总体的日负荷为所有电器期望功率叠加的总和,则单户家庭每个时间采样点的期望功率P(t)表示如下:
(14)
3 群体居民用电行为模型
每一类型的用户用电行为虽然具有相似性,但是由于家用电器组合情况、家用电器功率大小及用电时间点存在差异,这一类型居民用户的总期望功率不是典型家庭用电功率的简单累加.本节采用蒙特卡洛模拟将上述因素纳入模型.
3.1 家用电器组合模型
对于某种家用电器,每户家庭只存在2种情况,即拥有和不拥有.因此,每户家庭某种家用电器的拥有情况可以采用0-1分布表示如下:
(15)
式中,xdi表示家庭d是否拥有家用电器i,0表示不拥有,1表示拥有;Rdi为由[0,1]均匀分布产生的随机数;pdi为家庭d家用电器i的拥有率,其值与不同的家庭类型相关,可由国家统计局给出的数据获得.
3.2 家用电器功率分布模型
由于每个家庭使用的电器品牌、年限等不同,同一种电器的实际功率存在差异.假设每种家用电器的功率可以表示为以家用电器的平均功率为中心的正态分布,其概率分布函数为
(16)
式中,χi为典型家庭家用电器i的实际功率值;μi为典型家庭家用电器i的平均额定功率值;σi为家用电器i功率分布方差.
3.3 用电时间点分布模型
假设同类型的家庭在所有时刻的用电行为相互独立,且在相同时刻具有相同的用电行为特性.若样本群体数量足够大,则这些同类型家庭的用电时间序列满足中心极限定理,即某类家庭用户某一用电行为发生的时间点近似服从正态分布.因此该类所有用户服从期望为典型家庭用户用电行为发生在某一时间点方差为σ的正态分布.本文中假设居民用户家庭的方差σ为10 min.考虑用电时间点分布后的tn时刻该类用户群体的期望功率Pf(tn)为
(17)
式中,bu为该类用户群体中用户的数量;n为时刻tn在一天采样点中的序数;f(tn)为概率密度函数;P(tn)为tn时刻该类典型家庭的用电功率;tpn为分布起始时刻;tqn为分布结束时刻;n1为起始时间序数;n2为结束时间序数,分别定义如下:
(18)
(19)
(20)
(21)
(22)
3.4 蒙特卡洛模拟
蒙特卡洛算法是一种以统计和概率原理为基础的随机模拟运算方法,又被称为随机抽样法或者统计模拟法,在物理学、金融工程学及电力系统等领域都有应用.本文基于由智能电表[20]采集的数据,采用非序贯蒙特卡洛算法,对影响群体用户用电行为的各个随机量进行随机抽样,以得到群体用户用电情况的统计值.
首先,根据预测精度Δtp,将一天划分为np=(24×60)/Δtp;然后,读取群体用户类型,调用相关类型的家用电器拥有率,进行蒙特卡洛随机抽样,记录抽样结果;接着,读取该用户类别的典型家用电器功率,构造家用电器功率分布模型,进行蒙特卡洛随机抽样,记录抽样结果;由以上2次抽样计算出该类别用户群体第q个家庭中的电器基本信息Iq,即
(23)
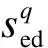
随后,获取该用户类别下典型家庭的用电行为概率,对典型用电行为时间点进行蒙特卡洛随机抽样,获得各个家庭的用电行为状况;结合以上3次抽样情况,计算得出该类别群体用户的用电行为预测结果,即
(24)
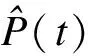
4 算例仿真
本文利用MATLAB仿真软件对该家庭的用电行为进行分析和预测.以江苏某地一智能插座示范小区100户家庭为例,基于由小区居民家庭中安装的智能电表收集的历史数据可建立相关数据库,并根据已经建立的群体居民用户用电模型,对小区居民的用电行为进行分析和预测,以验证该模型的准确性.选取该小区2017年6月1日—30日和7月1日—29日的信息作为历史数据,预测2017年7月30日—7月31日该小区的用电情况,同时选取该小区从2017年11月1日—30日和12月1日—29日的信息作为历史数据,预测2017年12月30日及12月31日该小区的用电情况.各户居民家庭以10 min为间隔采集7种典型家用电器的用电情况,分别是热水器、冰箱、电视、洗衣机、电磁炉、日光灯、空调,同时采集每天的基础信息,包括气象信息、日期信息等,并将这些数据分别保存至Excel文件中.选取早高峰时间点等值作为特征值将用户类型预归纳为3类,即上班族家庭、老人家庭、上班族+老人家庭.
4.1 仿真结果
4.1.1 相似日仿真分析
考虑到每个特征因子的重要程度不同,采用灰色关联度分析法确定人体舒适度因子、日期差距因子、星期类型因子及重大事件因子的权重,计算结果分别为0.357 02、0.276 60、0.209 35和0.157 03.
在相似日提取模块中,基于4个特征因子的权重值对历史日与预测日相似度特征向量进行分析,夏季预测日以7月31日为例,可以提取出5个相似日分别为6月6日、6月9日、7月10日、7月28日及7月24日,冬季预测日以12月31日为例,可以提取出5个相似日分别为11月4日、11月16日、12月10日、11月26日及11月11日,结果如表1所示.
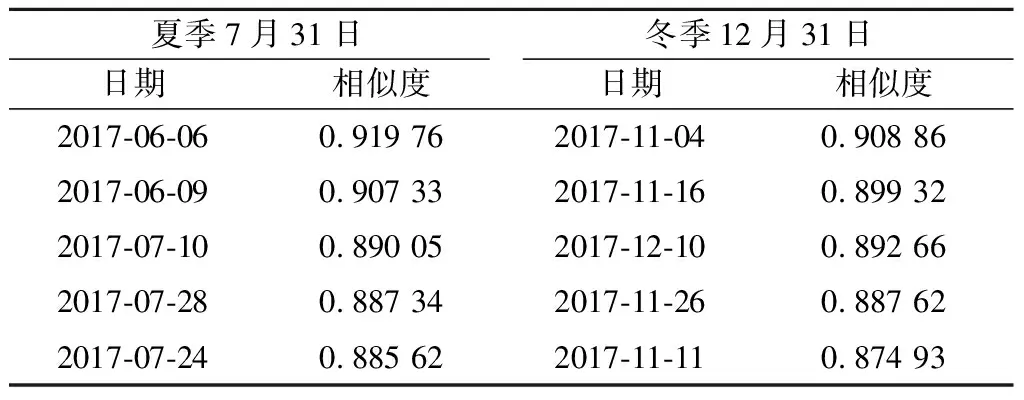
表1 相似日提取结果
4.1.2 家庭聚类仿真分析
读取各家庭的特征数据,利用FCM算法进行聚类分析.设定聚类目标为3类时,从图1仿真结果看出,特征值的选取合理,3类用户类别明晰,聚类效果较好,其中Ⅰ类家庭25户,Ⅱ类家庭52户,Ⅲ类家庭23户.根据聚类结果特点,本文将其中家庭类型Ⅰ的居民用户称为上班族家庭,家庭类型Ⅱ的居民用户称为上班族+老人家庭,家庭类型Ⅲ的用户称为老人家庭.分别对每类用户的日负荷排序,根据排序结果及电器使用情况,分别选取3种家庭类型的典型用户.
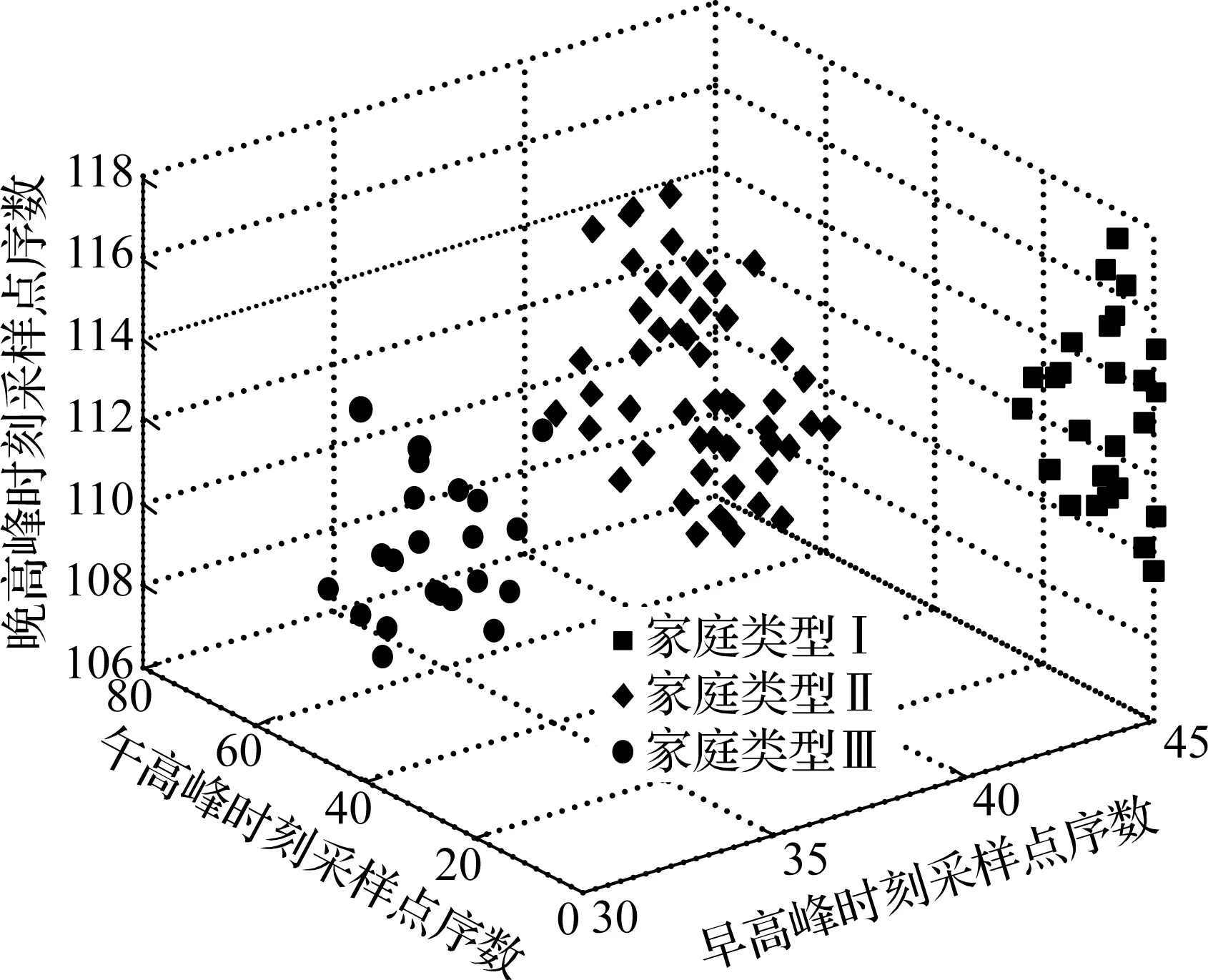
图1 家庭聚类分析结果
4.1.3 用电行为仿真分析
根据历史数据,可以得到所有家用电器的行为预测结果.以夏季7月31日Ⅰ类上班族家庭的部分电器行为概率结果为例,如图2所示.7种家用电器的预测使用概率与实际使用情况较为相符,如电磁炉在18:00—20:00之间工作的概率达到100%,预测日当天使用时段区间大致位于18:30—19:30,包含于预测时段区间.

(a) 洗衣机
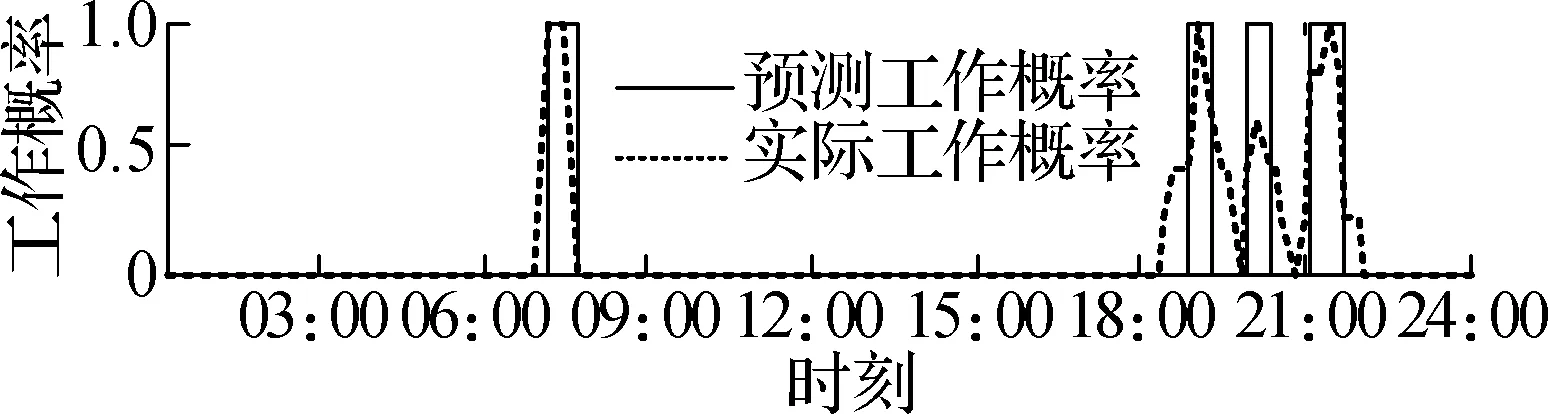
(b) 热水器

(c) 电磁炉

(d) 电视
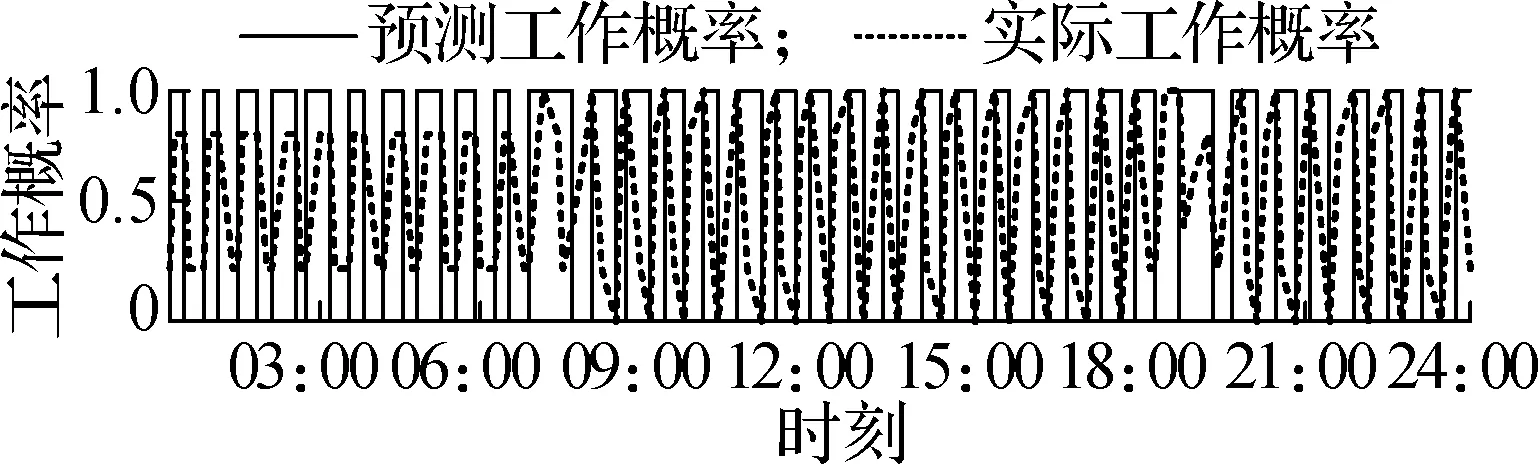
(e) 冰箱
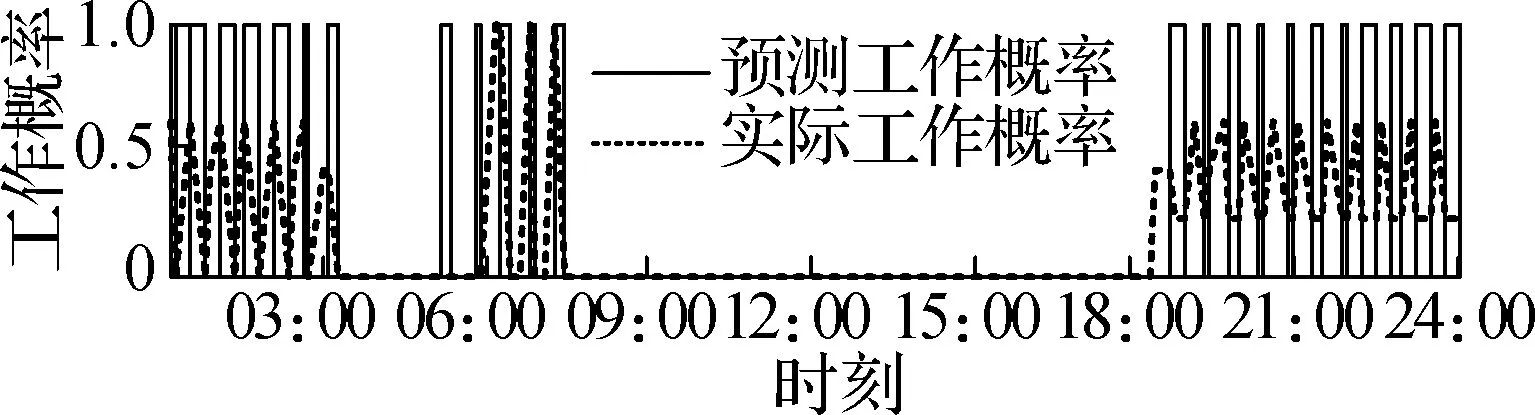
(f) 空调
4.1.4 用户蒙特卡洛模拟仿真
对3类家庭用户用电行为分别进行蒙特卡洛模拟抽样,抽样值选为1 000.以12月31日及7月31日为例,仿真结果如图3所示.
通过抽样均值分析各类家庭在预测日的用电行为,可知冬季上班族家庭用户群体存在早晚2个用电高峰,晚高峰持续时间较长,峰值也明显高于早高峰峰值,其余时间呈现明显的功率低谷,夜间谷值高于白天谷值,用电时间非常集中,峰谷差明显;上班族+老人家庭用电量明显高于上班族家庭,上午和中午的峰值密集且峰值大小相近,构成持续一段时间的用电峰值期,也存在晚高峰,晚高峰峰值相比上午和中午峰值更高,该类家庭用电低谷持续时间较短,大部分时段都处于较高功率用电的状态;老人家庭呈现全天用电行为更为分散的特点,但同样存在早中晚3个用电高峰,峰值与谷值的差距较小,用电行为更具随机性.夏季用电情况类似,但是总体用电量略低于冬季用电量.由于后2类家庭用户用电行为具有更明显的分散性,可以认为其对需求侧管理的参与度会相应地高于上班族家庭用户.
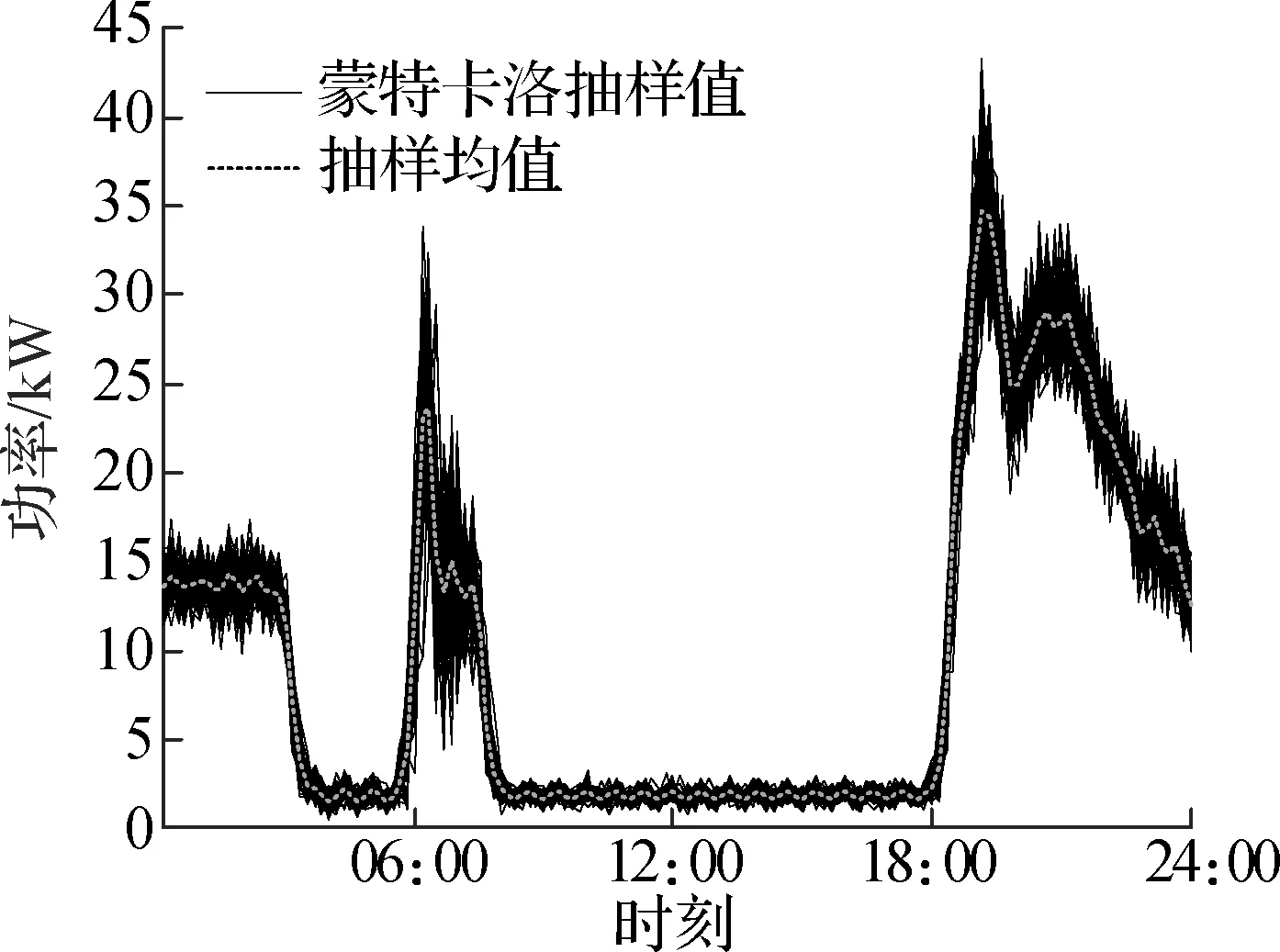
(a) 冬季上班族家庭

(b) 夏季上班族家庭
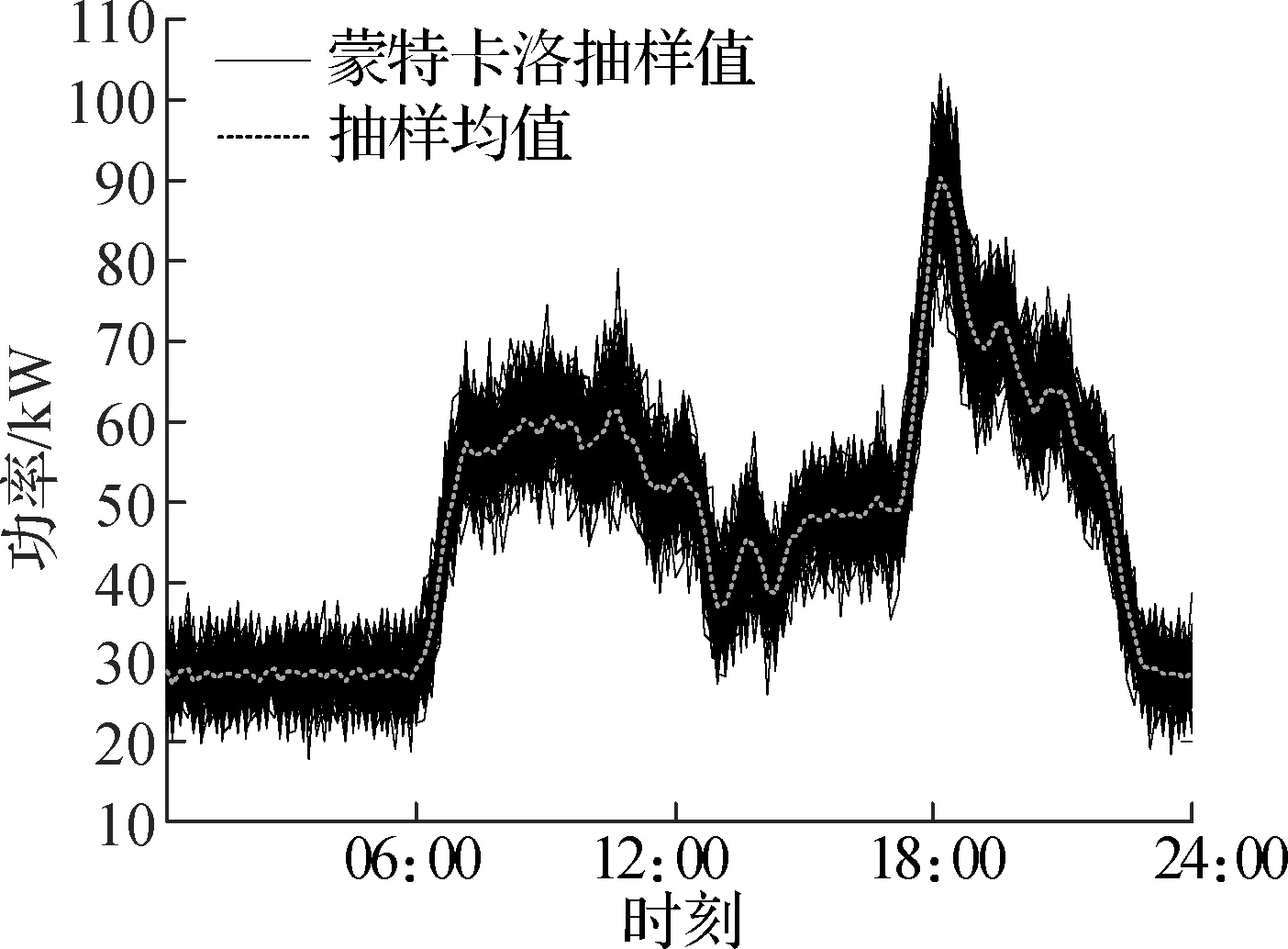
(c) 冬季上班族+老人家庭
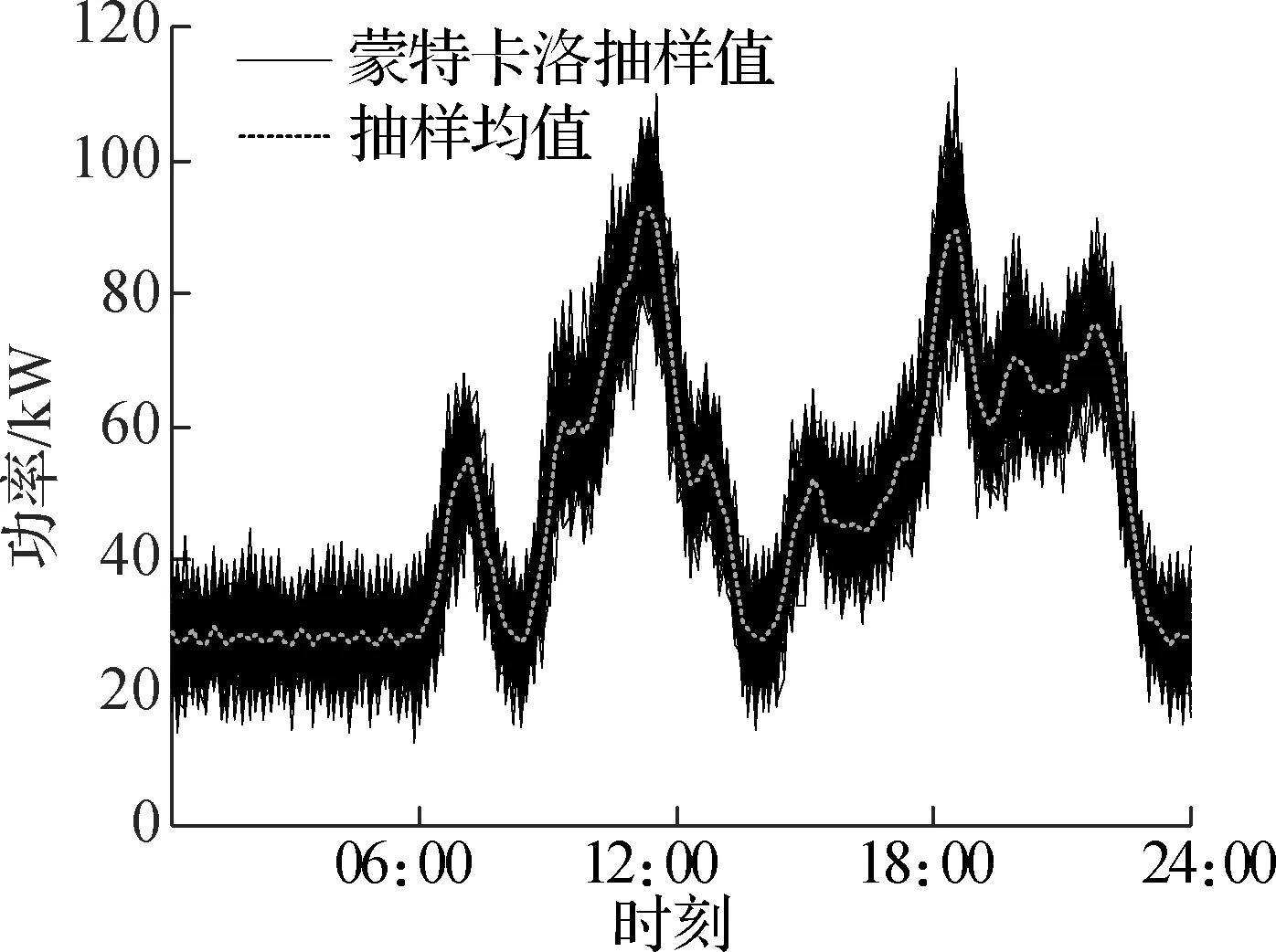
(d) 夏季上班族+老人家庭
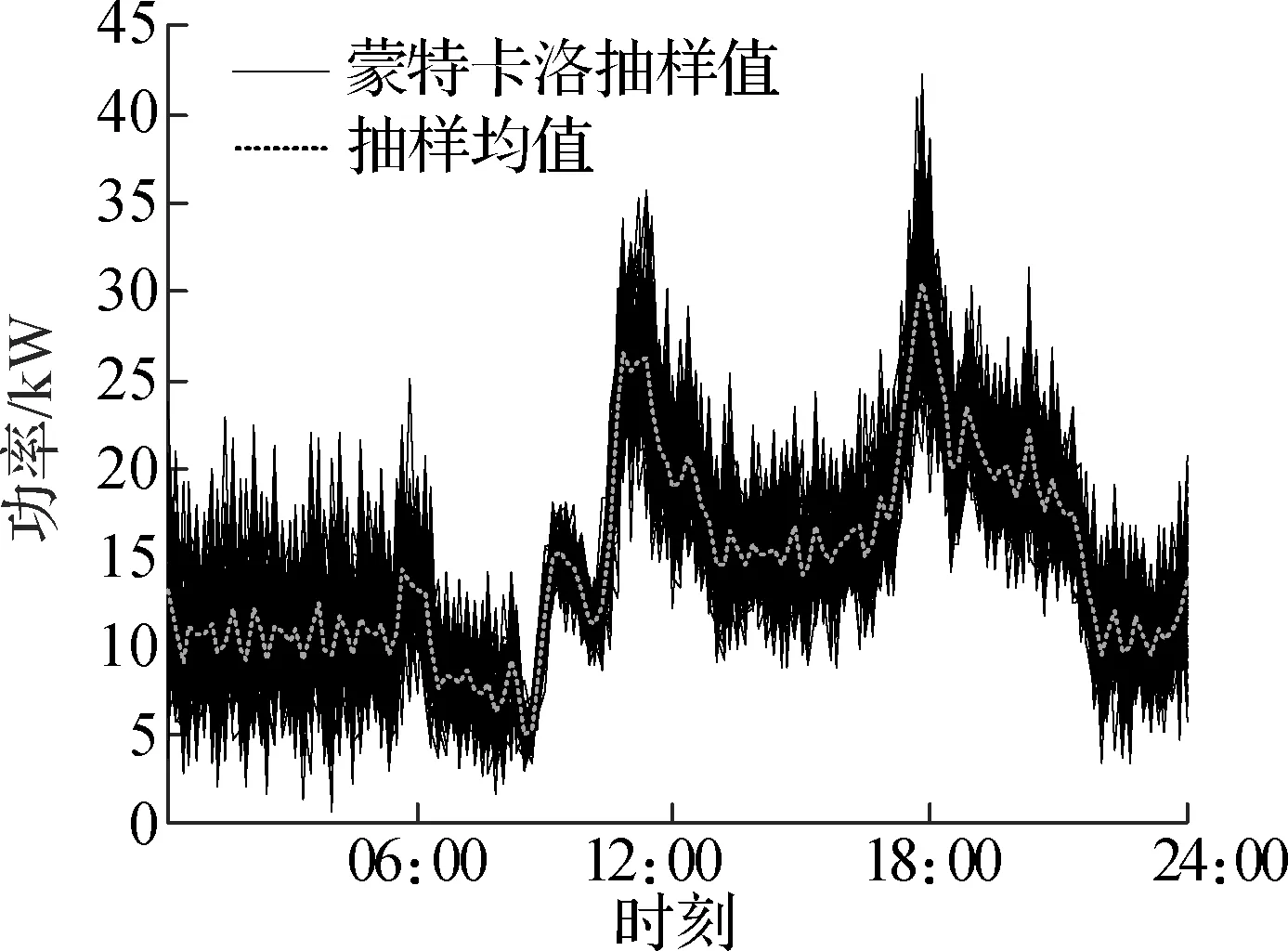
(e) 冬季老人家庭
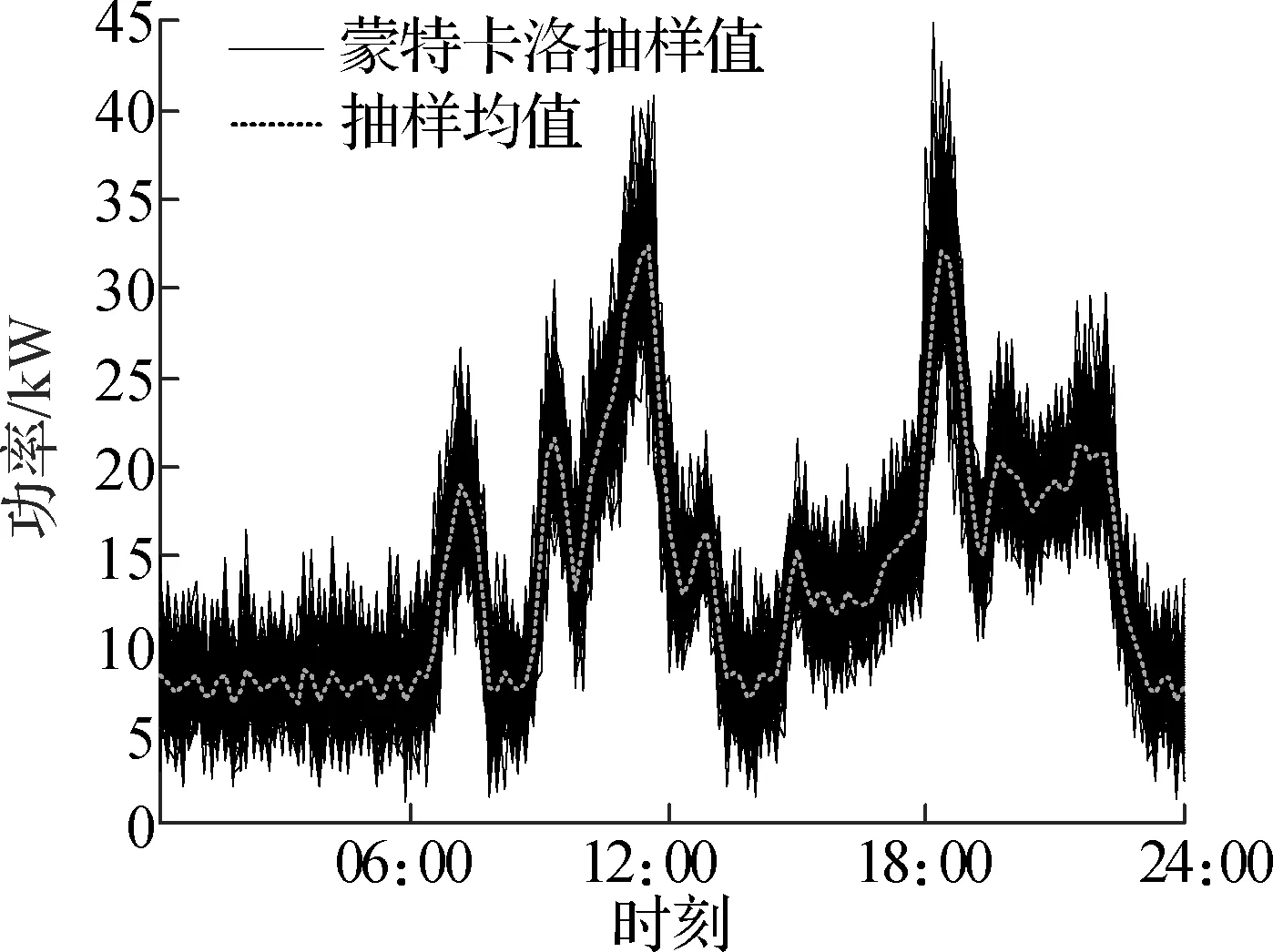
(f) 夏季老人家庭
4.1.5 群体用户用电期望功率仿真
在3类家庭用户分别进行蒙特卡洛模拟的基础上,仿真出最终小区总体用户用电功率期望,冬季12月30日和12月31日小区总体用户用电功率期望以及夏季7月30日和7月31日小区总体用户用电功率期望分别如图4和图5所示.图5为仿真结果与实测值的相对误差.从仿真结果可以看出,冬季12月30日全天的预测误差绝对值最大值为14.01%,出现在下午17:30;12月31日全天的预测误差绝对值最大值为13.56%,出现在上午11:00;夏季7月30日全天的预测误差绝对值最大值为13.95%,出现在上午05:00;7月31日全天的预测误差绝对值最大值为12.28%,出现在中午13:55.
4.2 模型对比
为了验证本文方法的有效性,将基于蒙特卡洛模拟的自下而上建模方法(本文方法)与聚类后不进行蒙特卡洛抽样的方法(方法1)、基于相似日的灰色模型预测方法[14](方法2)及基于相似日选取的BP神经网络模型预测方法(方法3)进行比较.相对误差ε定义如下:
(25)
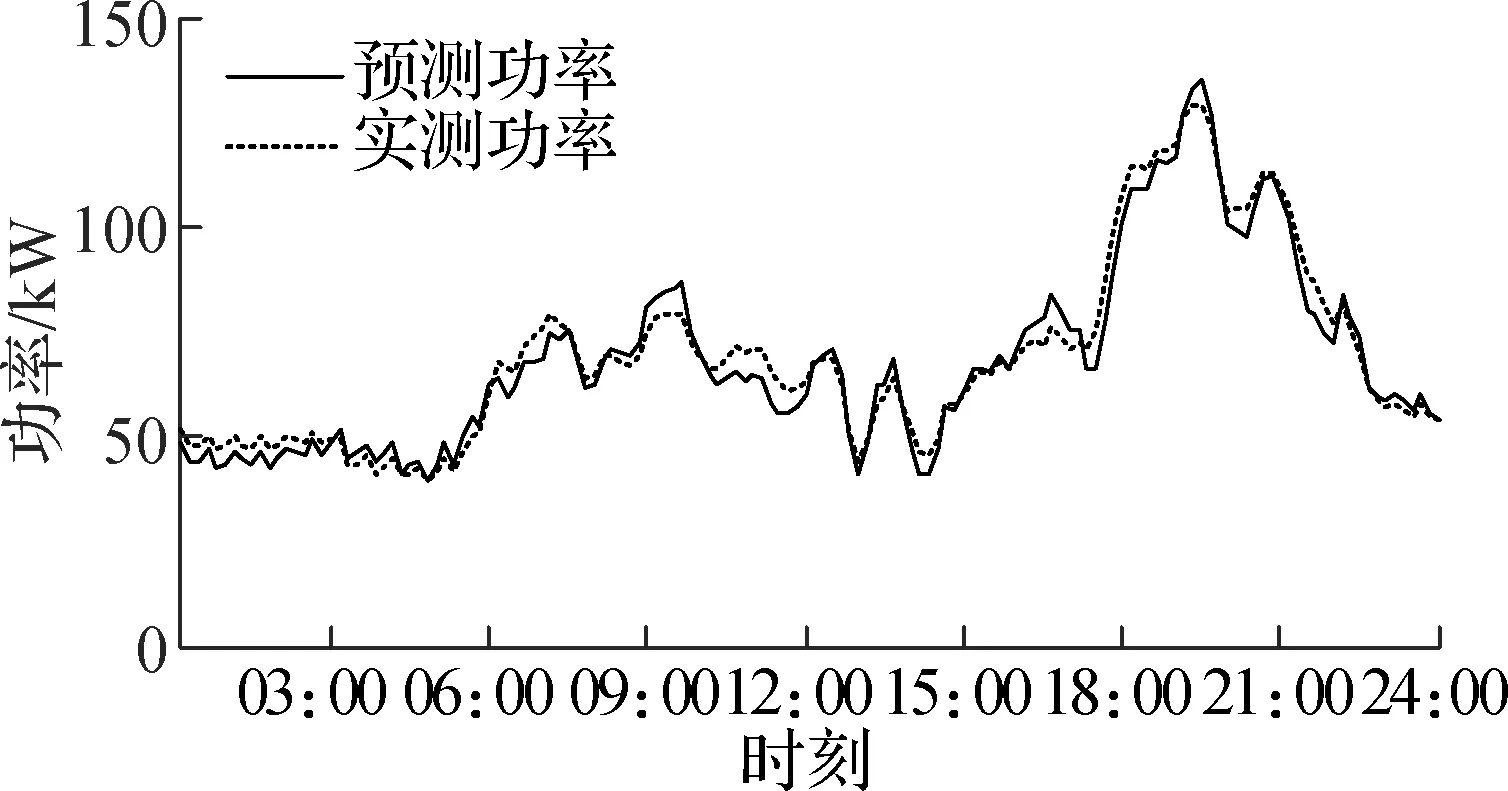
(a) 2017-12-30
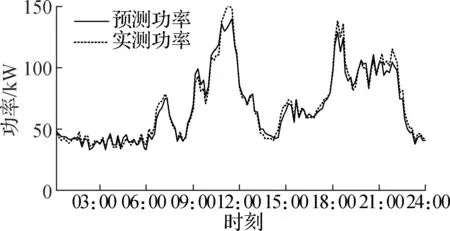
(b) 2017-12-31

(c) 2017-07-30

(d) 2017-07-31
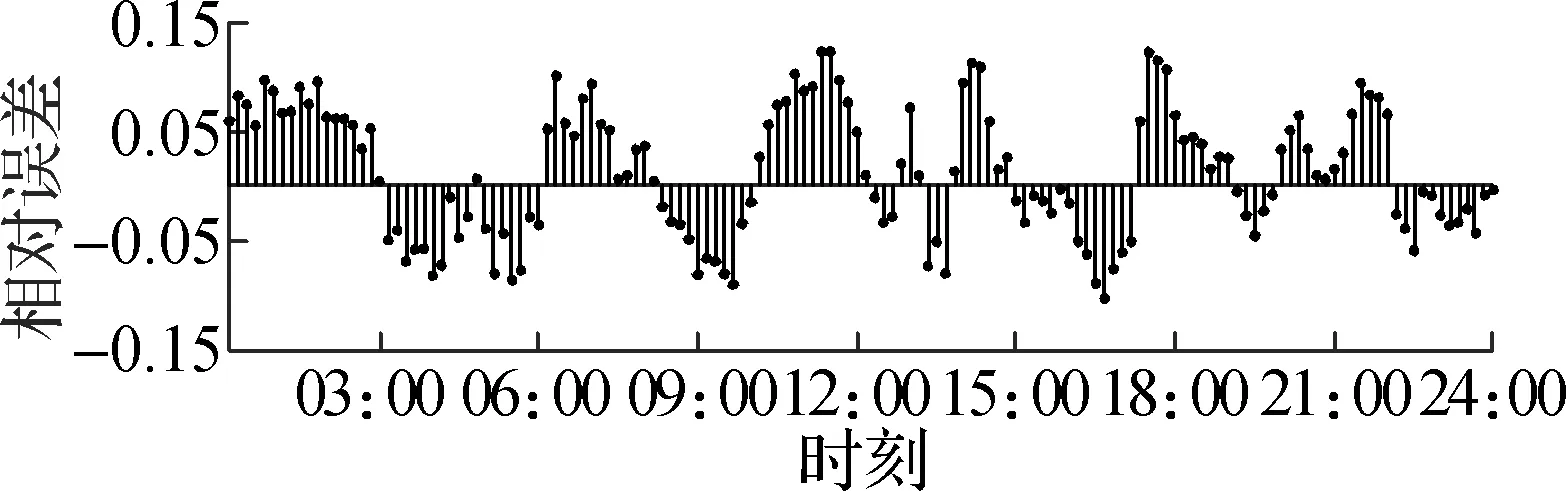
(a) 2017-12-30
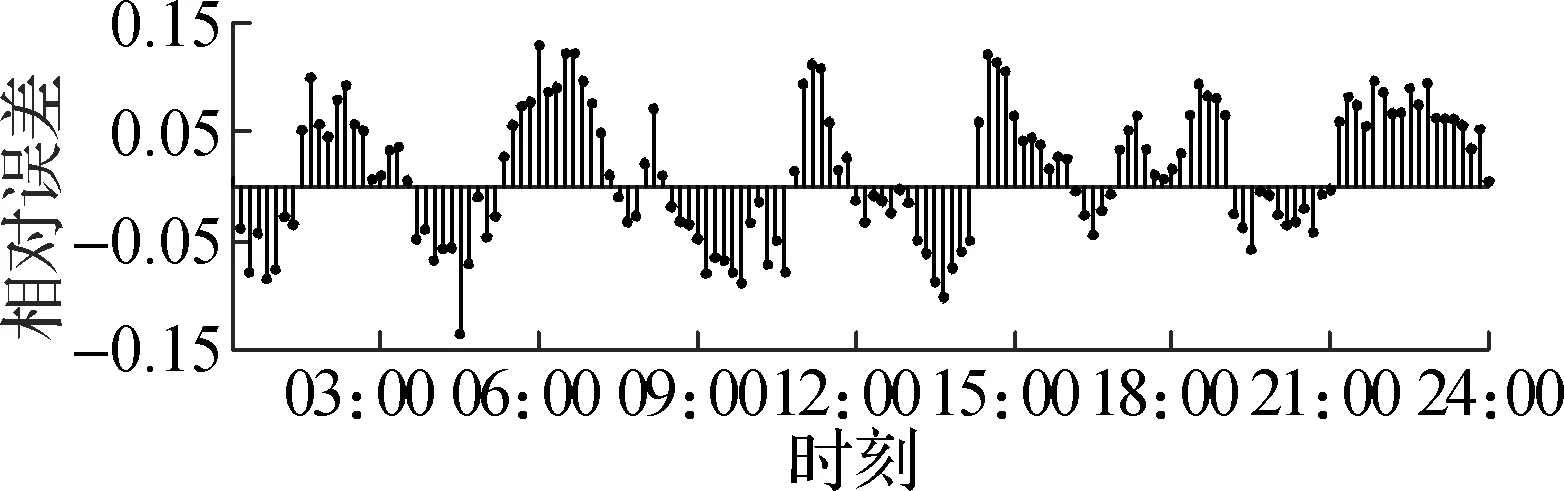
(b) 2017-12-31
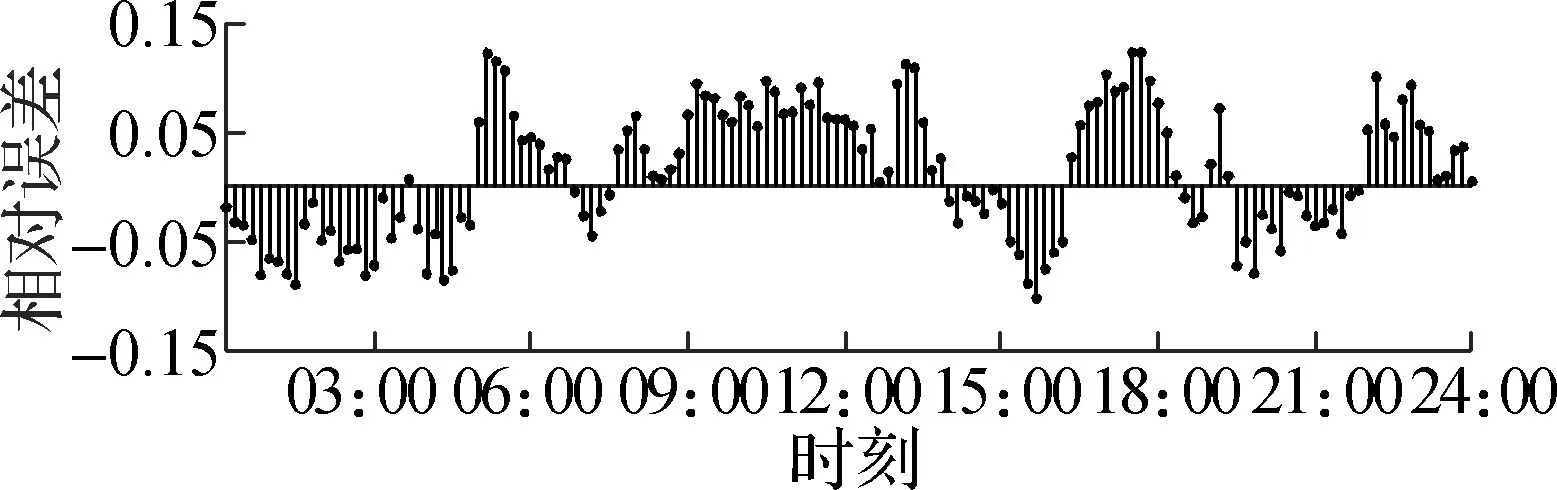
(c) 2017-07-30
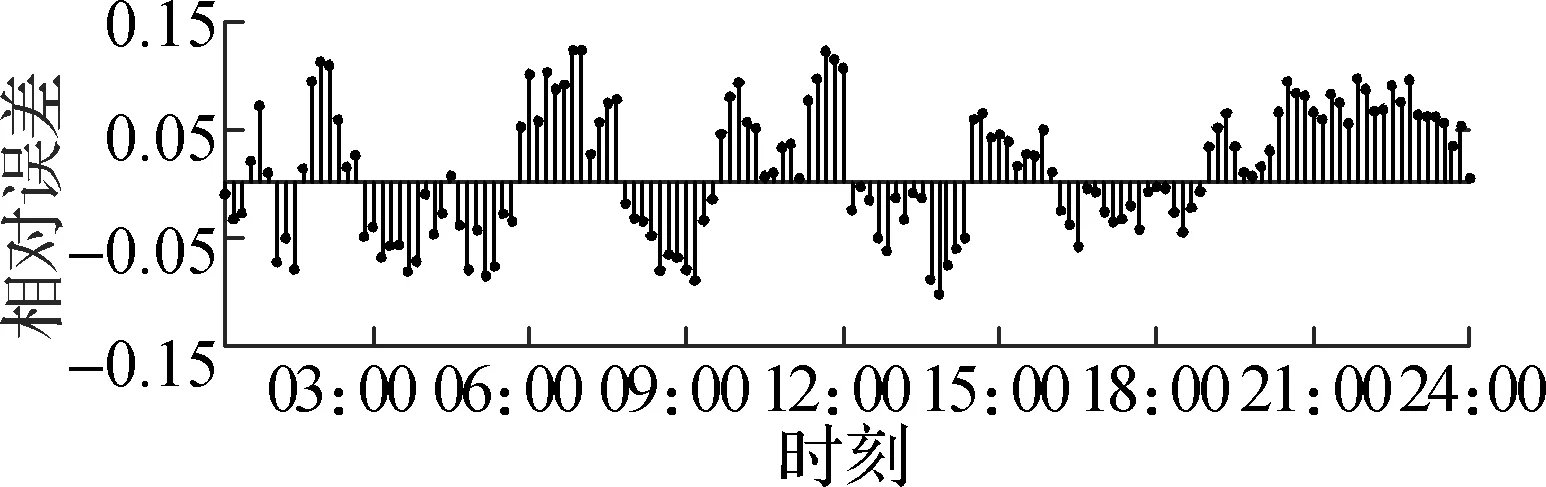
(d) 2017-07-31
式中,Pp为功率预测值;Pm为功率实测值.
以夏季预测日7月31日为例,预测日负荷最大值、最小值、平均值的误差如表2所示.

表2 夏季群体负荷最大、最小、平均值仿真结果与实测值误差
由表2可看出,本文方法的平均功率预测值与实测值误差为1.3%,而采用上述方法1平均功率误差值达到4.1%,方法2平均功率误差值达到2.7%,方法3平均功率误差值达到2.3%.同时利用本文方法得出的仿真值与实测值的最大误差为5.6%,低于分别采用方法1、方法2、方法3得出的7.1%、7.5%和6.9%.可见采用本文方法预测的功率值与实际测量值有较高的一致性,且相对于其他2种方法有一定的优越性.
5 结论
1) 采用自下而上的建模方法,将群体居民用户负荷预测建模划分为相似日提取、聚类分析、用户用电行为分析和用户负荷预测4个模块,能够全面描绘群体用户用电情况.
2) 蒙特卡洛随机抽样可以较好地模拟大样本下居民用户用电中的随机因素,有效提升预测精度.实际算例分析结果表明,本文所提方法的负荷预测平均误差为1.3%、最大误差为5.6%,较经典的灰色模型和神经网络方法在预测的平均误差和最大误差2方面均有显著改善.
3) 本文预测方法的数据通过智能电表获得,当居民用户数量增加时,由于智能电表的普及,此方法仍能够实现较准确的预测,有较大的现实意义.
4) 本文中单个用电设备的数据是基于智能插座进行采集的,由于智能插座无法安装在每一户居民家中的所有设备上,有一定的局限性.但是随着非侵入式检测负荷监测技术的日渐成熟,提出的预测方法可基于该技术得到各个用电设备的数据进行应用.
