复合材料壳体挂机飞行一体化结构优化设计分析 *
2020-01-16张蕾蕾宋学宇贾有军
刘 鎏,张蕾蕾,宋学宇,3,贾有军,刘 浩
(1. 中国航天科技集团有限公司四院四十一所,西安 710025;2. 西安微电子技术研究所,西安 710000;3. 西北工业大学 航天学院,西安 710072)
0 引言
随着导弹武器作战半径的不断扩展,未来高性能空基导弹对于壳体结构轻量化的要求日趋提高。国内现有空基导弹发动机壳体及吊挂主要采用金属结构。王云霞等[1]对某挂机用固体火箭发动机壳体吊挂加强结构进行了强度计算与分析,给出了严酷载荷工况下吊挂加强结构的应力分布规律。何洁等[2]对某型导弹吊挂结构建立了以几何尺寸为设计变量、以结构重量极小化为目标的吊挂优化模型,得到了满足功能条件的最优模型。何新党等[3]基于Patran/Nastran有限元分析软件的二次开发建立了用于导弹吊挂强度分析的参数化、自动化方法。
相比复合材料壳体而言,金属壳体结构易腐蚀、质量大,受钝感弹药(M)刺激,如烘烤和弹射撞击时反应剧烈[4]。近年来为降低空基导弹系统质量,提高导弹系统的动力性能,空基导弹壳体复合材料化已成为必然的发展趋势。美国飞马座固体运载火箭就是空基复合材料壳体技术的典型应用,此外美国还开展了“快速到达”空射火箭、“平流层”和“运载器一号”空基火箭的研制,火箭发动机均采用的是复合材料壳体。
本文主要研究空基复合材料壳体/挂机一体化结构,通过拓扑优化和多参数目标驱动优化对复合材料壳体挂机飞行一体化结构进行了优化分析,对挂飞连接结构进行减重设计,同时对结构关键尺寸进行参数敏感性分析。
1 结构优化分析理论
复合材料壳体挂机飞行一体化结构设计基本原则是在满足结构外部载荷环境要求的前提下实现结构的轻量化设计,即将结构的承载能力作为标的指标,通过优化分析方法来使结构质量达到最轻[5]。结构优化设计通常包括拓扑优化和尺寸优化,其中拓扑优化属于概念设计阶段,尺寸优化则属于详细设计阶段。
本文基于拓扑优化和多参数尺寸优化对复合材料壳体挂机飞行一体化结构进行详细优化设计。
1.1 拓扑优化原理
拓扑优化就是在结构内部实体化区域进行减材化设计,使结构能在满足应力、位移等约束条件下,将外载荷传递到结构主要承载位置,保证结构质量和承载能力的最优匹配,充分发挥结构力学性能[6]。拓扑优化首先需要确定结构优化区域并施加载荷及边界条件,然后选择有效的优化算法进行优化分析。常用的拓扑优化分析方法[7-9]包括变厚度法、均匀化方法及变密度法。
本文通过变密度法来建立材料密度与材料特性之间的关系,具体分析流程如图1所示。
1.2 尺寸优化原理
尺寸优化原理就是将结构关键尺寸(设计变量)进行参数化设计,在考虑结构外部载荷及环境(目标函数)的前提下对结构关键尺寸进行优化设计[10]。尺寸优化问题的数学表达式[11]如下:
Z= [z1,z2,…,zn]
F(Z)=Umin[f1(z),f2(z),…,fm(z)]
式中Z为设计变量;F(z)为目标函数;Umin(z)为求解最小值的函数。
约束条件:
ai≤zi≤bi(i=0,1…n)
hj(z)=0 (j=0,1…p)
gk(z)≤0 (k=0,1…q)
式中n为设计变量的个数;ai和bi为第i个设计变量的上、下限;hj(z)和gk(z)为选择函数,控制所选变量为最优解;p为非上、下限等式约束的个数;q为非上、下限不等式约束的个数。
具体分析流程如图2所示。

图1 拓扑优化分析流程图
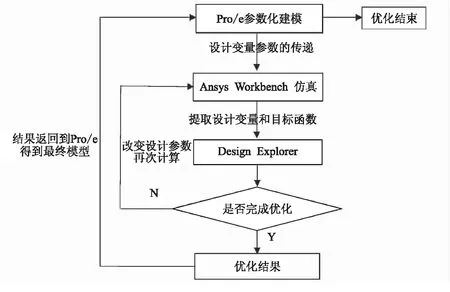
图2 多参数尺寸优化分析流程图
2 复合材料壳体挂机飞行一体化结构优化设计分析
2.1 金属挂机结构拓扑优化分析
复合材料壳体挂机飞行一体化结构(图3)主要包含复合材料壳体、挂飞结构、外缠绕层等,其中金属挂飞结构属于导弹和飞行器连接的关键结构件,在保证壳体和飞行器可靠连接的同时承受着着陆、飞行等不同的载荷工况。本文首先基于拓扑优化原理对金属挂飞结构进行优化分析,寻求结构质量和强度的最优配比关系。
金属挂飞结构采用高强铝合金,对应的材料性能参数如表1所示。根据复合材料壳体相关尺寸及两者之间的配合关系对挂飞结构进行初步设计,设计结果如图4所示,挂飞结构通过1#、2#、3#、4#与外部飞行结构连接,同时通过4道外缠绕层与复合材料壳体进行连接。

表1 铝合金材料参数
表2所示为各载荷工况下挂飞结构单个挂点载荷条件,取最恶劣的工况一对一体化结构进行分析,边界条件设定为固定壳体筒段两端面,同时在4个挂点施加载荷。
下面进行拓扑优化分析,分析对象为复合材料壳体、金属挂飞结构及外环向纤维缠绕层,由于挂飞结构支座质量占比较大,因此将优化区域设定为挂飞结构支座,取目标去除量为40%,计算结果如图5所示。图中红色区域为可移除部分。
对拓扑优化的结果趋势分析后进行形状拟合,拟合的过程中,以曲线简单易于加工为原则,并考虑到分析时约束边界条件与实际情况的区别,最终得到拓扑优化的结果如图6所示,优化前、后挂飞结构应力云图如图7所示,优化前后结果对比如表3所示。
优化前结构质量8.6 kg,最大Mises应力123.04 MPa,位于挂飞连接支座根部,而铝合金强度极限450 MPa,说明结构存在冗余质量;优化后鞍型座结构质量6.0 kg,最大Mises应力292.44 MPa,位于挂飞连接支座连接孔附近,事实上挂飞连接支座经形状拟合后连接孔下部被掏空减薄,从而导致结构最大应力点转移至连接孔附近,优化后结构质量由8.6 kg减少至6.0 kg,减重效果明显。
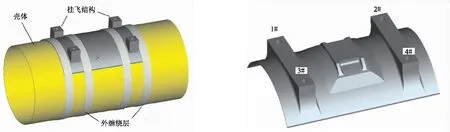
图3 一体化复合材料壳体结构 图4 金属挂飞结构
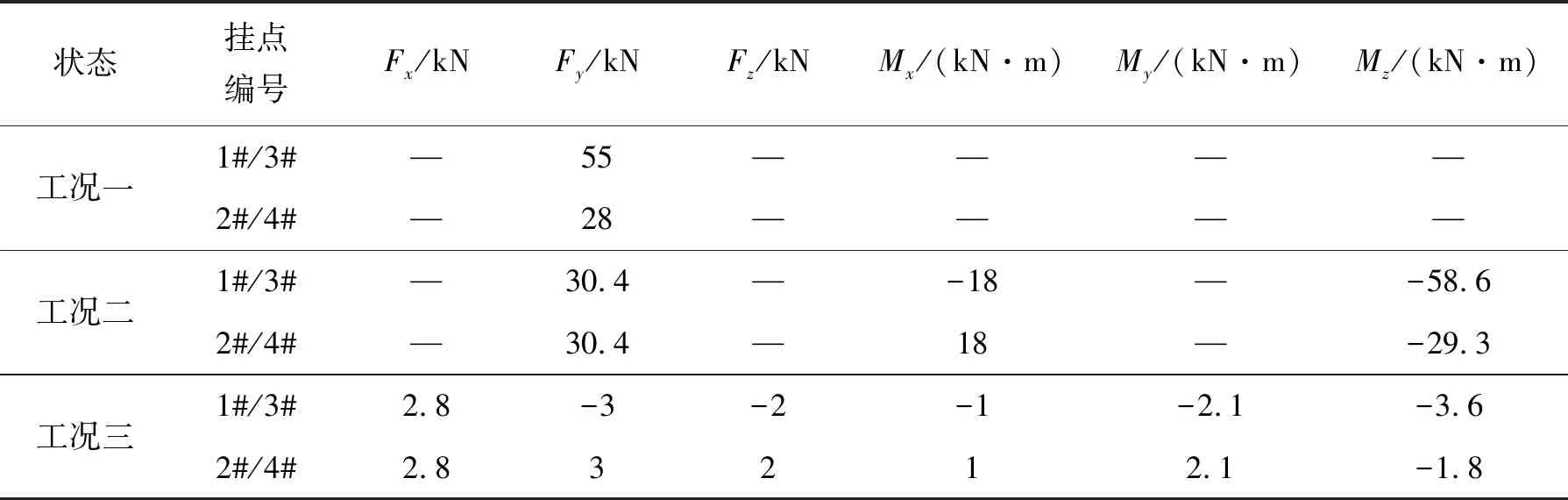
表2 载荷工况

图5 挂飞结构目标去除量为40%时的结果 图6 拟合结果
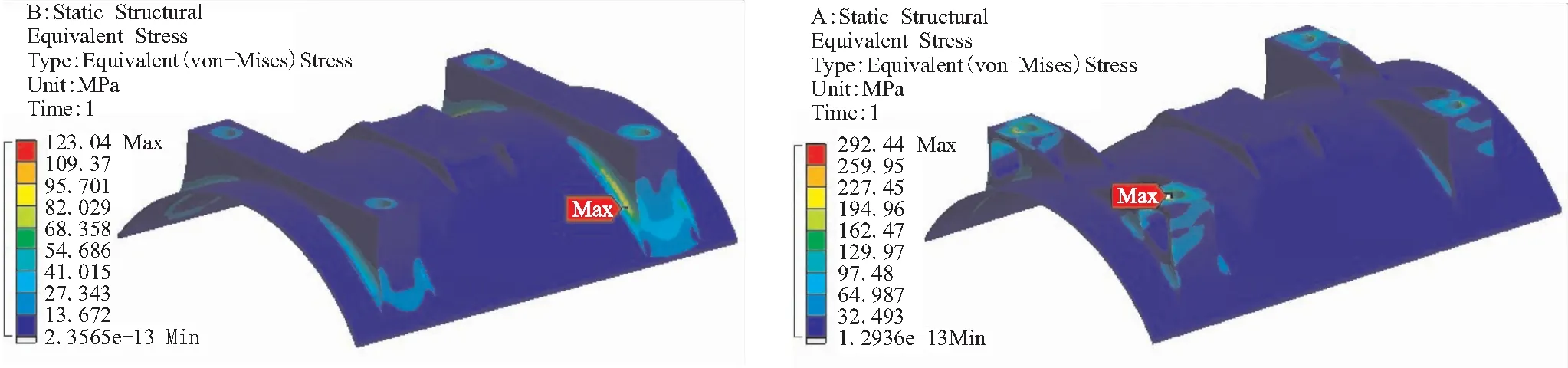
(a)优化前 (b)优化后

表3 拓扑优化前后结果对比
2.2 复合材料壳体挂机飞行一体化结构多目标参数尺寸优化
复合材料壳体挂机结构包含金属挂飞结构、挂飞结构外缠绕层、弹性层、内环向层、复合材料壳体等。其中复合材料壳体可依据常规理论及经验公式进行设计,因此本节参数优化关注的重点在于挂飞结构以及挂飞结构与复合材料壳体的外部缠绕层。本节基于PROE参数化建模平台和Ansys Workbench多目标参数优化模块的协同仿真来实现金属挂飞结构与复合材料壳体一体化设计分析。
2.2.1 材料参数
复合材料壳体为各向异性材料,不同于传统的金属材料,复合材料结构设计与分析具有一定困难,材料设计与结构设计相辅相成不可分离。复合材料结构分析大多基于经典层合理论。研究表明,该理论尤其适应于面内尺寸大于结构厚度2个数量级的复合材料结构。大多数复合材料压力容器都是薄壁结构,因此本文基于经典层合理论对复合材料壳体参数进行赋值。
2.2.2 优化参数
设定优化参数如图8所示。

图8 一体化结构优化参数
图8中,a1、a2、a3、a4为挂飞结构外纤维缠绕层宽度;b1、b2、b3、b4、b5、b6、b7、b8为挂飞连接支座单边棱板厚度;c1、c2、c3、c4为挂飞连接支座上肢板厚度(c3、c4图中未显示)。在PROE平台通过约束关系设置保证a1=a2=a3=a4=P3-DS_1,b1=b2=b3=b4=b5=b6=b7=b8=P2-DS_3,c1=c2=c3=c4=P1-DS_2,如图9所示。同时,确定优化的输出参数为挂飞结构质量和等效应力。
图9 一体化结构参数化设置
表4给出了各设计变量的初始值及搜索范围,即一体化结构设计状态参数初值,同时,依据一体化结构自身的设计要求,给出了各设计变量优化搜索范围,为实验设计的执行和优化算法提供采样空间边界及优化搜索范围。

表4 设计变量初值及搜索范围
2.2.3 多目标参数优化结果分析
对参数化模型进行多目标参数优化,所得实验设计结果如表5所示。实验设计是通过改变过程的输入因素,观察其相应的输出响应的变化,从而获得关于这个实验的相关信息,确定各个输入因素的重要性以及各个输入因素如何影响输出响应,并如何达到最优方案的目的。表5列举了不同采样参数下所对应的结构输出响应,可以看到采样点(50,12,5)所对应结构最大Mises应力最小,质量最大;采样点(50,7,5)所对应结构最大Mises应力最大,质量最小。结构质量越大,同种工况下结构最大Mises应力越小,多目标参数优化的目的就是找到结构质量和强度的一种最优平衡。
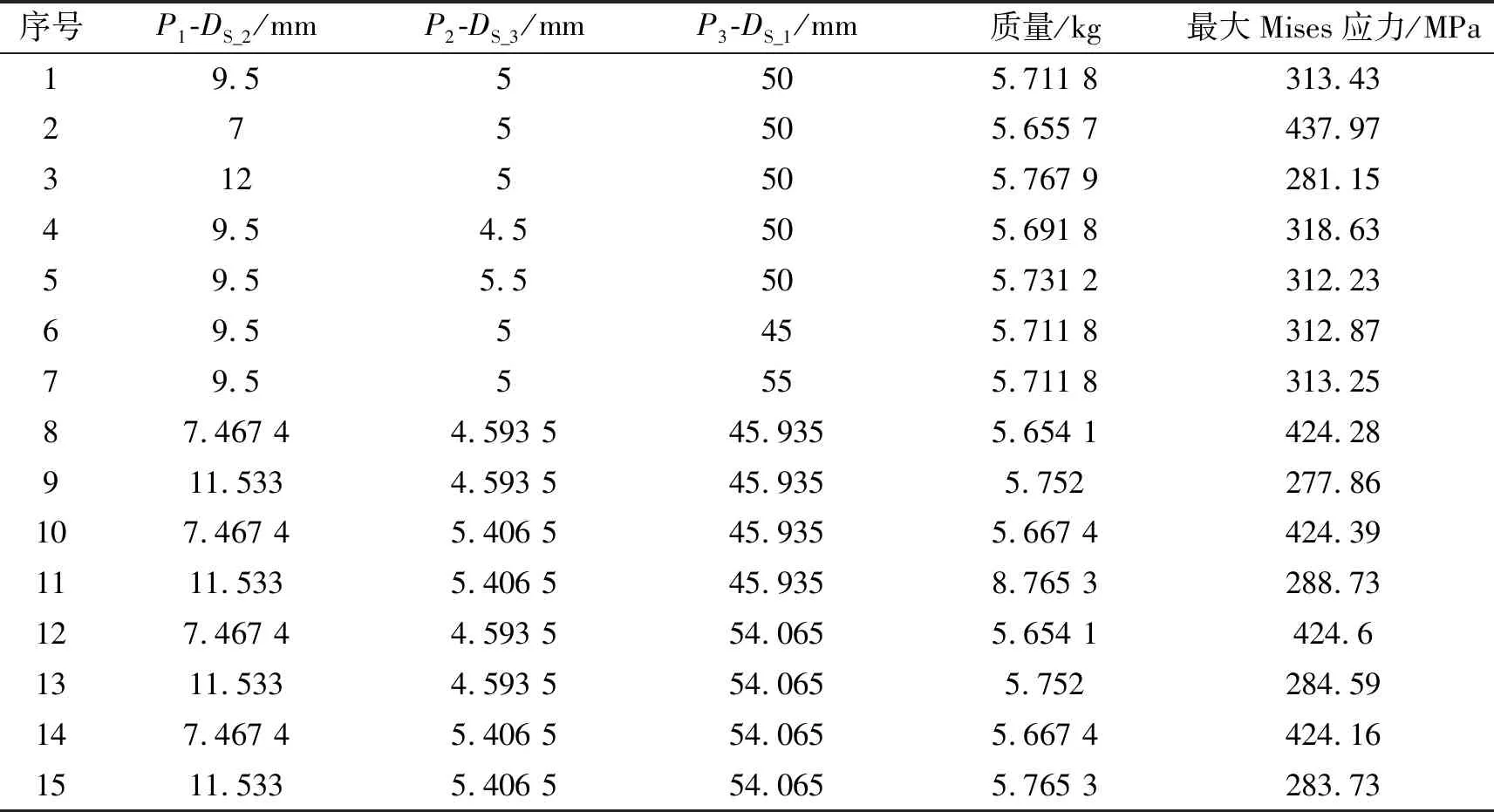
表5 多目标优化实验设计结果
图10为目标函数与输入参数的响应面曲线,其中两个横坐标表示挂飞结构外缠绕层宽度(P3-DS_1)、单边棱板厚度(P2-DS_3)、挂飞连接支座上肢板厚度(P1-DS_2)3个参数中的2个参数,纵坐标为目标函数(结构质量或结构最大Mises应力),响应面曲线反映了各目标函数与两两输入参数之间的对应关系。
图11为目标函数对各输入参数敏感性分布图,可看到目标函数对挂飞连接支座上肢板厚度(P1-DS_2)敏感性最高,对挂飞结构外缠绕层宽度(P3-DS_1)的敏感性最低。
图12为采样点(50,7,5)下外环向纤维层环向应变云图,可看到当单个外环向纤维层宽度为50 mm时最大环向应变为437.775 με,应变数值较低。外环向纤维层存在较大强度裕度,但考虑结构连接的可靠性,外环向纤维宽度不宜过低。
综合以上分析,对于挂飞结构而言,挂飞连接支座上肢板厚度(P1-DS_2)为影响整个优化结果的关键尺寸。结合表5所示实验设计结果,选定(50,7,5)为最优输入参数,对应的结构质量为5.94 kg,最大Mises应力为437.97 MPa,此时结构利用率得到较大的提高。

(a)P3-DS_1,P1-DS_2,Mises应力关系 (b) P3-DS_1,P1-DS_2,质量关系 (c) P3-DS_1,P2-DS_3,Mises应力关系

(d)P3-DS_1,P2-DS_3,质量关系 (e) P1-DS_2,P2-DS_3,Mises应力关系 (f) P1-DS_2,P2-DS_3,质量关系

图11 目标函数对各输入参数敏感性分布图
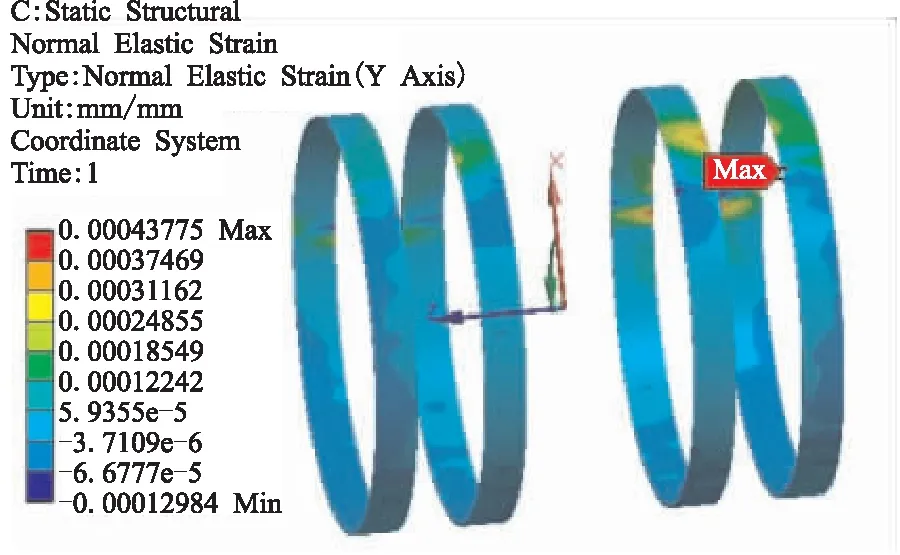
图12 环向纤维环向应变云图
3 静力载荷破坏试验
为对本文优化设计方法进行进一步验证,对研制的复合材料壳体及挂机结构进行静力载荷破坏试验,将发动机壳体通过前、后裙与前、后承力底座连接,再将连接好前、后承力底座的试验件固定在承力平台上,通过作动筒对吊耳施加法向载荷,试验如图13所示。
试验采用逐级加载方式进行,随着载荷的逐级递增,壳体及挂机结构应变在10~140 kN前应变与载荷基本呈线性增长,当超过140 kN后挂机结构外部环向纤维开始断裂,随后挂机结构出现断裂,图14为挂机结构测点载荷-应变关系曲线。

图13 试验布置图
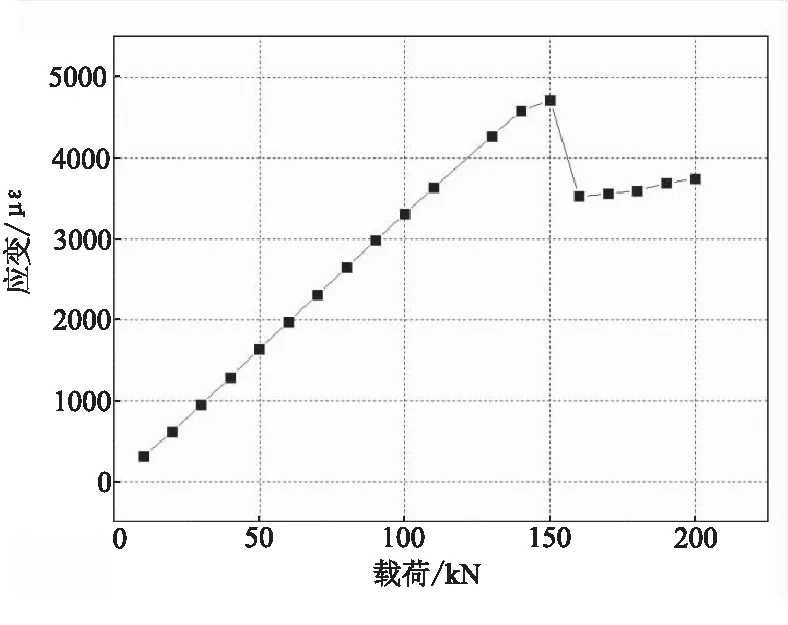
图14 测点载荷-应变曲线
4 结论
(1)对挂飞结构进行拓扑优化分析,实现了结构形状的优化设计,优化后结构质量由8.6 kg降低至6.0 kg,减重效果明显。
(2)对于挂飞结构,挂飞连接支座上肢板厚度(P1-DS_2)为影响整个优化结果的关键尺寸,挂飞结构外缠绕层宽度(P3-DS_1)对结构整体优化结果影响较小。
(3)结合实验设计结果,选定(50,7,5)为最优输入参数,对应的结构质量由5.72 kg进一步降低为5.66 kg,最大Mises应力为437.97 MPa,复合材料外环向缠绕层最大环向应变为437.775 με,结构满足要求。
(4)通过静力载荷破坏试验验证本文设计方法,设计最大工况载荷为166 kN,实际静力试验破坏载荷为140 kN。分析原因是最大工况作用于挂机结构均布的4个螺纹孔;而静力载荷试验载荷作用于挂机结构单一吊挂,结构在同等载荷情况下更易发生破坏。
