基于压缩感知的非重构频谱检测方法
2020-01-16沈振惠毛祥芳
文/沈振惠 毛祥芳
1 引言
随着无线通信技术的迅速发展,智能家居、远程医疗等无线新业务的不断增长,人们对无线频谱资源的需求量日益增多,频谱资源匮乏和频谱利用率低的矛盾变得愈加严重,成为阻碍无线通信发展的瓶颈。认知无线电(Cognitive Radio, CR)技术为解决该问题开创了新的途径。认知无线电技术不需要增加新的频段,能够利用空闲的频谱向CR用户开放,CR用户可以在不对授权用户通信造成干扰的前提下以衬底式或机会式地使用这些频谱,从而提高频谱利用率。为了避免干扰授权用户通信,CR用户应时刻监测周围频谱环境,频谱检测是认知无线电技术的前提与基础。
由于宽带频谱利用率低,具有固有的稀疏性,压缩感知(Compressed Sensing,CS)成为利用亚奈奎斯特采样率实现宽带频谱感知的一种很好的选择。Z.Tian 等人[1]利用Sub-Nyquist 采样率实现了信号的重建,进而实现频谱感知。S.Hong 等人[2]提出一种基于贝叶斯压缩感知框架的检测方法,该方法不需要完全重构信号,而是直接利用压缩测量值来对授权用户信号进行参数估计。Zhao等[3]提出了一种顺序宽带频谱检测的方案,实现更高精度的频谱感知。Gao等人[4]提出了在非重构的压缩感知框架下,利用特征值的特性进行频谱感知,能够降低计算复杂度。
2 压缩感知理论
频谱感知理论由Donoho和Candes于2006年首先提出,是一种新的数据采集技术。该理论利用信号在某域的稀疏性,以远低于奈奎斯特速率对信号进行压缩采样,可应用于宽带频谱感知的数据采集阶段,能显著降低宽频谱信号高速率采样所带来的硬件压力和数据处理量。
在压缩感知理论中,信号的稀疏表示可以实现信号的降维压缩,即将信号在某个正交基下进行分解,得到的系数向量中只包含较少的大系数,其它系数都趋近于 0。在较低的频谱利用率环境下,信号在频域是稀疏的。
稀疏表示后的信号可以利用观测矩阵进行降维处理。假设有观测矩阵其中M 假设CR网络需要感知的频谱处于100MHz~120MHz之间,整个频谱被划分为20个带宽相等互不重叠的子信道,假设有f3、f11、f18三个活跃频带,在每个活跃频带上,生成二进制相移键控BPSK信号,经过sinc波形成形滤波后发送出去。假设CR用户接收到得宽带信号模型为 图1:基于压缩感知的非重构频谱检测方法框图 图2:奈奎斯特采样信号及频谱 图3:随机压缩采样信号及频谱 其中,Pi和fi分别表示第i个信道上的能量和中心频率,B表示带宽, 在低频谱利用率情况下,CR用户接收到的信号在频域是稀疏的。根据压缩感知理论,对稀疏信号可以采用随机采样的方式就可以恢复出原始的信号。但是,很显然的一点是,我们无法直接在频域进行采样,只能在时空域对信号进行采样。 CR用户对接收到的授权用户数据在时空域按远低于奈奎斯特的速率对信号进行高斯随机压缩采样,然后利用傅立叶变换矩阵对应的列将压缩数据变换到频域,作为授权用户信号的频谱估计,滤波后采用合适的门限进行判决,得到频带内频谱的使用情况,原理框图如图1所示。该方法不需要重构信号,减少了重构算法的复杂运算。 根据上述系统模型对提出方法进行仿真,图2为奈奎斯特速率(往上取2的整数幂)采样的授权用户信号波形和频谱图,图3中“o”为随机压缩非均匀采样信号及滤波判决后的频谱图,平均采样速率为是奈奎斯特速率的1/8。 本文提出的非重构频谱检测方法利用随机矩阵理论直接在时空域对中频信号进行压缩采样,采样频率远低于奈奎斯特速率,然后利用傅立叶变换矩阵将随机压缩数据变换到频域,作为授权用户的谱估计进行频谱检测。该方法具有计算复杂度低、感知性能稳定等优点。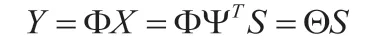
3 系统模型与压缩频谱感知算法


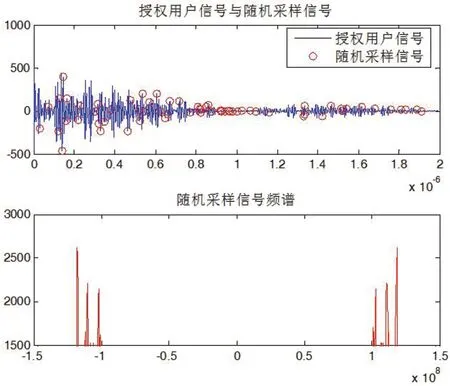

4 算法仿真与结果分析
5 结论
