基于高精度几何基元的圆弧工件匹配方法

文/李岩 卢曾鹏 刘富凯 李西卫 刘克平

随着国内制造产业的转型升级，对制造流程智能化、自动化的需求在不断加深，机器视觉技术[1]作为实现机器人智能化的核心技术被应用的范围越加广泛，由起初的电子制造业和半导体生产，发展到了包装，汽车，交通和印刷等多个领域。在半导的获取体生产中，设备需要根据机器视觉获取的芯片位置信息调整拾取头，准确拾取芯片；在医疗检测方面，对生物芯片的检测，放射科的X 放射等，通过引入机器视觉系统，完成对图像信息、传输、计算与应用；在武器领域中，武器弹药依靠嵌入式机器视觉系统中图像采集和处理设备，在发射后可以自主寻找、判定、选定和攻击目标；在工业生产领域，无论是零配件装配，商品的定位分拣还是电子元件的识别检测都需要获取图像，从而按照工作要求完成目标的识别、定位、抓取等任务。目标匹配与定位作为机器视觉的一个重要研究方向[2-5]，引发众多学者对其进行深入研究。

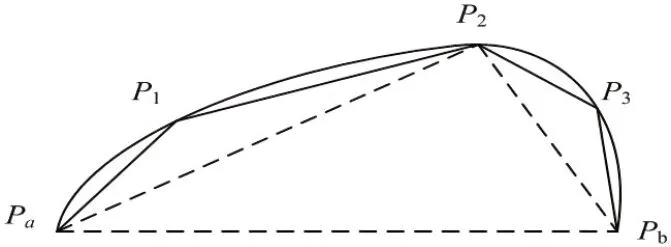
图1：多边形近似示意图

1971年，Leese 提出了MAD 算法，该算法思想简单，具有较高的匹配精度，被广泛应用于图像匹配当中。基于MAD 算法，Barnea和Silverman 提出了SSDA 算法，在之后的研究中，又提出了NCC 归一化积相关算法[6-7]，该类算法利用灰度值完成图像的匹配任务。Lowe 提出了一种从图像中提取特征不变量的方法SIFT 尺度不变特征图像匹配算法，通过对极值点的检测来实现对特征点的定位，并在特征点的邻域范围内构建特征描述子，通过计算各特征描述子之间的欧氏距离完成对图像中目标的匹配[8]。王瑶等人提出一种基于改进SIFT 的快速自适应图像匹配算法，通过简化特征点描述子的生成过程，提高算法的效率，并且使用自适应调整距离比阈值参数，提高了算法的鲁棒性[9]。许多学者研究发现，使用特征点进行目标匹配与定位的计算量大、耗时较长。因此，Mahmood 等人利用相关性的传递性，提出了基于相关性的匹配度量的消除算法，用以对目标图像进行识别与定位，在减少计算量的同时，保证了图像识别定位的精度[10]。Li 等人提出了一种基于线特征的目标图像匹配与定位方法。对 Canny 算子进行改进，并提取边界中的线段特征，并应用长度与方向作为约束条件，生成各线段对应元组信息，通过与度量线进行相似性对比来筛选出能够保证精确识别的目标元组[11]。刘红敏等人提出了一种基于基元表示的多边形检测方法，利用关键点及边缘信息来对基元信息进行定义，并通过将定义好的基元重组为多边形的方式完成目标区域边缘的检测，该方法的提出为多边形目标的匹配与识别定义了一种新的思路[12]。周晴等人提出了一种使用圆弧基元对工件进行匹配与定位的方法来完成对工件的实时定位，该算法具有较好的实时性，但定位精度有待提升[13]。

针对圆弧工件匹配率低、鲁棒性差、定位不准等缺陷，本文提出一种基于高精度几何基元的圆弧工件匹配方法。整个过程由离线模板构造和在线匹配与定位两个阶段组成。离线阶段，运用多边形近似算法逼近目标轮廓，获取轮廓分割点；用最小二乘法拟合的几何基元来获取参数；构建线扩散函数模型，通过对几何基元参数信息的计算来确定目标位姿；在线阶段，获取目标工件的最大圆弧基元，通过最大圆弧基元完成对工件的粗定位，并在此基础上，利用最大圆弧基元的旋转信息以及求得的对应基元的距离信息，完成对工件信息的精准获取。实验结果表明，该方法能够针对含有圆弧工件图像的匹配和定位具有较高的实时性和普适性。

1 高精度几何基元的提取

几何基元提取最常用方法有基于变换域、梯度、链码的方法，其中最具代表性的有Hough 变换法[14]、相位编组法[15]、链码跟踪法[16]。其中，Hough 变换法存在占用内存大、耗时长等缺点；相位编组法受噪声影响大、分组误差易产生断裂的短直线，而链码跟踪的原理简单，能够得到基元的位置、方向、长度等信息，实时性较好。因此，采用8 邻域规则跟踪工件轮廓，获取轮廓点信息，从而进行几何基元的提取[17]。

1.1 线扩散函数模型

准确提取目标轮廓序列在目标识别分析中起着重要作用，而常规边缘检测梯度算子的精度不能满足高精度目标轮廓的要求。因此，针对一些高精度轮廓[18]、椭圆[19]等特征的提取，采用线扩散函数模型。

其基本原理如下所示：设目标区域边缘的灰度值曲线呈刃状分布，且边缘点的灰度值信息与该边缘点的灰度值信息存在关系，则定义其目标函数为：

式中，S(x)表示线扩散模型，该模型在服从高斯函数分布特征。

如上式所示，ρ 表示灰度值密度分布的标准差；x 表示边缘点与该点法线的距离。将式（2） 代入式 （1）中，通过法线方向上的偏微分，可以获取目标边缘像素的梯度特征函数。

根据式（3）可知，图像边缘像素点处的梯度可以等效为图像工件边缘点法线方向距离r 和线扩散函数密度分布参数ρ 的函数。因此，将式（3） 进行线性化变换为：

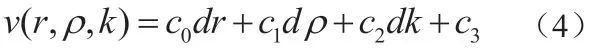
式中，常数项c0、c1、c2、c3、可以利用求取偏微分获得。为了方便求解，将公式中参数的初始值定义为：

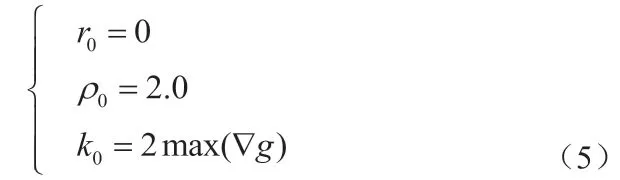
上式中，设参数k0的值为区域最大梯度值的2 倍，其目的是为了保障拟合曲线扩散函数的曲线接近真实曲线。根据测量平差原理，式 （4）为间接平差方程，依据最小二乘法原理，该模型解为：

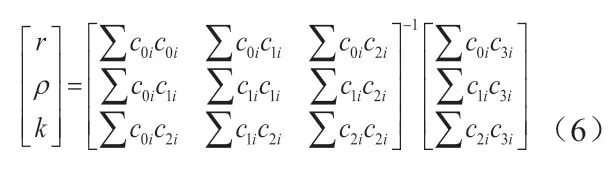
1.2 多边形近似

针对平面曲线的多边形逼近的迭代方法评估[20]，大多数情况下的表现良好。而通过8 邻域跟踪得到工件初始轮廓，需要进行拟合几何基元。因此，采用该算法进行多边形近似，具体步骤如下：

当目标轮廓连续且为闭合曲线时，选择整条轮廓区域的中点作为分割点将整条区域分割为两条线段。

（2）由式（8）计算轮廓上任意一点P(x，y)到直线 的距离d。

图2：模板图像

（3）如图1所示，P2为目标轮廓点，通过P2将和所构成的曲线轮廓进行分断。循环步骤（2），记录所有符合筛选条件的目标轮廓点，通过对这些目标轮廓点的连线，构建该区域轮廓的近似多边形。

1.3 最小二乘法拟合几何基元

通过上述近似迭代算法得到符合距离阈值的分段点，通过各分段点之间的连线构成的多边形以代替原图中的圆弧区域。为了保证拟合的准确性，减少过分割的产生，在对圆弧基元进行精确拟合之前，首先需要对分割的圆弧区域进行检测与重组。

将基元的长度信息作为主要分割信息实现对圆弧区域或线段的定位与匹配[13]。其基本流程如下：首先，设定一个长度信息的阈值T1，若目标基元的长度高于所设阈值，则认定其为直线基元，无需执行其他操作，可以直接进行拟合操作，并获取其相关参数；若目标基元的长度信息不高于所设阈值，且其相邻基元的长度信息不高于所设阈值信息，则标记定该基元为短基元，需要对该基元进行重组，首先，设通过最小二乘法采集到该基元的半径信息为R，将该短基元与其相邻的短基元合并后重新检测并进行拟合，通过最小二乘法获取到新的圆弧基元的半径R'，求取两个圆弧基元的半径差值，若该差值小于预设阈值Tp，则两基元合并，并搜索下一个相邻基元重复进行上述操作，直至将各区域中的短基元全部合并为长基元为止，将所得到的所有基元全部进行检测后，对所得各基元的参数信息进行计算。

1.3.1 最小二乘法拟合直线基元

为了实现轮廓点的直线拟合，拟合函数形式设置为y=kx+b，其中，k 表示直线的斜率，b 表示直线在纵轴上的截距。根据上文中得到的分段点的集合将这些分段点的坐标值代入直线方程中，并将计算值与实际值进行比较，计算其相对误差，设该误差为yi-f(xi)，以整体误差值最小作为判别基准，对k,b 的参数值进行求取。

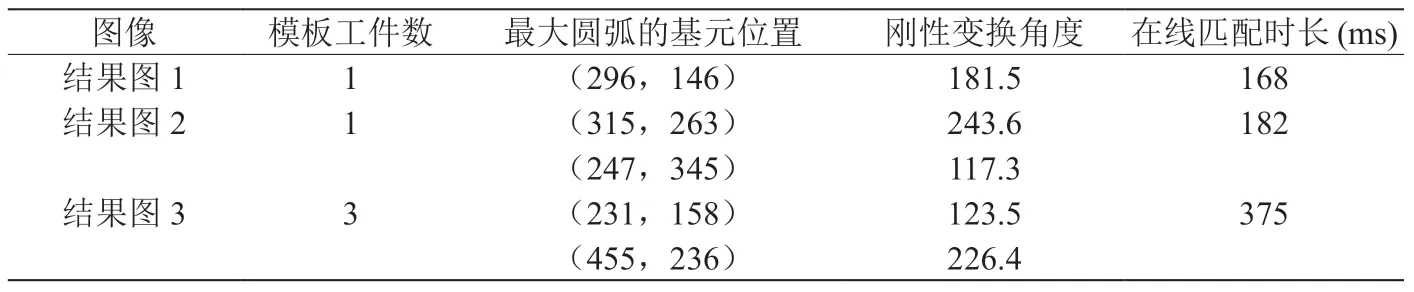
表1：算法匹配与定位参数表

图3：实测图像

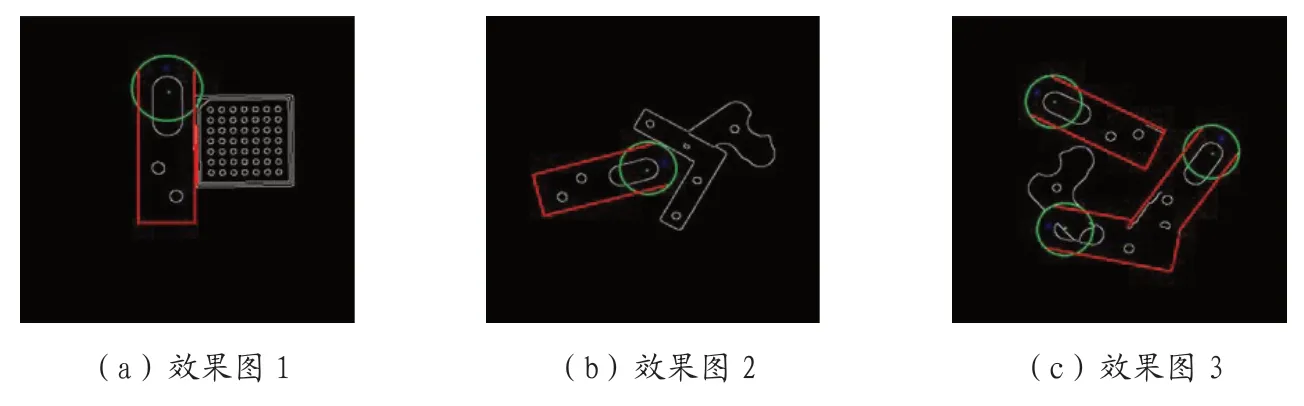
图4：实测工件匹配与定位效果图

1.3.2 最小二乘法拟合圆弧基元

利用圆弧特征对所求得轮廓点中的圆形区域进行拟合。设圆方程为：

式中，坐标(A,B)是圆心，R 是半径。而圆的参数方程为：

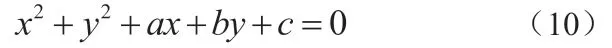
在轮廓点集 中，求取 到圆心距离的平方和圆形半径的平方的差，如式（11） 所示：

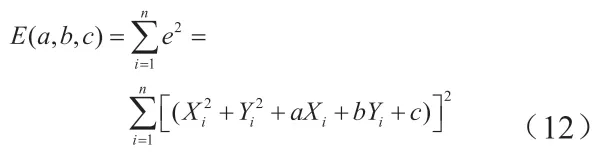
使 取到最小值，求得A、B、R 的估计拟合值。

2 基于高精度几何基元的圆弧工件匹配方法

2.1 离线模板构建

在离线阶段，首先对图像进行预处理，消除图像中噪声，并提取工件的边缘，根据8 邻域规则跟踪目标轮廓获取轮廓点。然后采用多边形近似方法对工件轮廓进行分割，采用最小二乘法拟合初始几何基元，得到初始几何基元参数。

2.1.1 轮廓点精确定位

通过线扩散函数模型精确定位初始几何基元的轮廓点，从而可以准确提取几何基元，具体流程如下：

（1）通过初始几何基元方程，采集几何基元样点并计算每个采样点的法向量。

（3）将所述{Gi}代入式（4）建立误差方程，然后通过式（6）最小二乘模型迭代运算得到

（4）每个样点的精确坐标可以通过式（13）和式（14）得到：

（5）上述操作完成后，对相邻的下一个分段点进行同步处理，直至所有样点处理完成，对这些样点进行拟合，以提取高精度几何基元参数。

2.1.2 模板位姿表示

2.1.3 计算基元间距离

通过上述方法可以获取到最大圆弧基元与剩余基元的距离信息。同时在线匹配和定位时的参考量，可以将模板基元之间的距离作为依据。

2.2 在线匹配与定位

依据上述流程同步处理采集到的图像实际信息。首先，在粗定位阶段，依靠图像信息采集的初始基元，采用线性函数模型对实测图像进行定位，并运用最小二乘法对几何基元进行拟合，记录各基元之间的位置信息与距离信息以定位最大圆弧基元；计算模板图像和实测图像两者之间变换的参数量，并对实际测量图像进行刚性变换。随后，利用两幅图像中剩余几何基元的角度信息与距离信息实现对目标匹配与定位。

3 实验结果与分析

为了验证本文提出方法的有效性，构建以MATLAB 为基础的仿真实验平台，选取HALCON 图片库中含有圆弧的工件图像，如图2和图3所示。

将本文所提出的方法应用于实测图像中进行测试，其结果如图4所示。

如图4(a) 所示，该图中存在一个模板工件和一个矩形工件，采用本文所提出的方法，实现了对模板工件的精准匹配，然而，在测试过程中，为了保证在线匹配的准确性，两种工件边缘之间的距离过近，因此，在匹配的过程中，将矩形工件的边缘识别为模板工件的一个待匹配基元，未能实现对工件的准确匹配。在图4(b) 中存在一个模板工件，通过对匹配结果的分析，可以得出，本文所提出的方法，在模板工件存在旋转、平移的条件下，仍可以实现对工件的准确匹配。在图4(c) 中，两个模板工件之间存在叠压现象，通过对匹配结果图的分析可以看出，本文方法能够成功的定位到未被叠压的工件部分的直线基元。

如表1所示为本文提出算法的具体实验参数。

随机选取100 组工件进行了测试，匹配正确达到98%，其中错误匹配的一幅图像如图5所示，通过对图像进行分析可以看出，图中共存在两个模板工件，但由于在多边形拟合的过程中，由于图像中其余工件的遮挡，工件的最大圆弧基元起点信息无法被获取，因此，原图中的两个模板工件只有一个可以被成功识别并准确定位，另一个模板工件未能被成功识别。通过对实验结果图的分析，其原因在于在获取工件最大圆弧基元的起始点信息时，由于其余元件的遮挡，因此未能获取到的工件起始点的准确坐标信息，因此，匹配过程中工件的方法发生了偏转，无法成功获取到该目标。

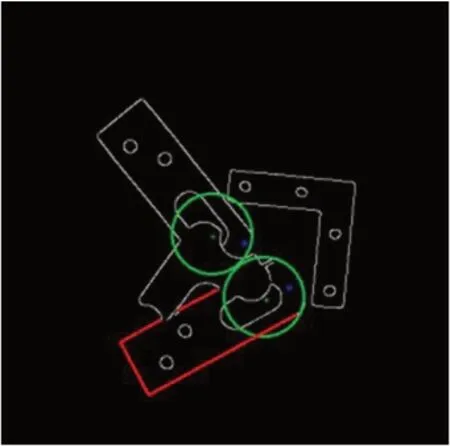
图5：错误匹配的结果图

4 结论

为了解决圆弧工件匹配成功率低，定位不准的问题，结合几何基元具有旋转不变性这一特点，提出了一种基于高精度几何基元的圆弧工件匹配与定位方法。首先，对图像中的集合基元进行拟合，利用线扩散函数模型完成对目标区域边缘的分段，获取准确的各基元的参数与各基元之间的相对位置信息，完成对工件的粗定位工作。利用剩余几何基元之间的位置关系参数，完成对模板图像与实测图像的精定位工作，从而完成对整个工件的精准定位。通过大规模的实验分析表明，本文所提出的方法针对含有圆弧的工件，能够实现对其的准确识别与匹配，并能够适应多目标，旋转，平移，以及部分遮挡状态下的对目标工件的准确匹配与定位。