政府补贴下两零售商竞争的闭环供应链协调研究
2020-01-16江苏大学管理学院江苏镇江212013
王 鑫,蔡 莉 (江苏大学 管理学院,江苏 镇江 212013)
0 引 言
2016年,国务院正式颁布实施了《“十三五”节能减排综合工作方案》[1]。该方案首次提出需要积极推动再制造产业的建设,并将办公、大型工业设备领域作为重点来推动再制造发展。近年来大多数企业积极响应国家政策致力于产品再制造的同时,也引发了国内外学者对闭环供应链的青睐。
归纳文献可见,目前闭环供应链涉及的主要研究内容包括:闭环供应链的网络设计研究、销售渠道选择研究、库存管理研究、协调机制研究等。然而闭环供应链的研究不仅旨在帮助企业有效地降低成本、提高自身的利润,更重要的是可以解决因过量生产造成的资源短缺和环境污染问题。
例如,就供应链的协调机制与定价决策,Savaskan[2]以分散式决策为基础对比分析第三方回收、零售商回收、生产商回收三种模式,并通过设计有效的协调机制提高闭环供应链的整体效率,最终得出零售商回收模式相较于另外两种方式更具有优势。郑本荣等[3]基于专利保护的视角,探讨了双渠道供应链中生产商的专利许可对供应链决策的影响。Wei等[4]依据两种不同渠道力量对比,研究了信息对称和不对称下的闭环供应链定价及回收问题。归纳发现,以上文献所假设的闭环供应链系统均未涉及多个同层成员间的竞争问题,仅为一个单一生产商、单一零售商和单一第三方的简单结构。然而,供应链系统同层成员间的竞争行为对供应链成员的各项决策均产生了重要的影响。在制造商竞争的环境下,部分学者基于政府补贴、成员合作、竞争强度等多视角对供应链决策的影响进行研究。Mitra[5]等探讨了制造商与再制造商之间相互竞争的情况下,政府补贴对废旧产品再制造的影响。Jena等[6]进一步研究了两制造商相互竞争的情况下,与零售商的三种不同合作方式对闭环供应链整体利润的影响。姚锋敏,滕春贤等[7]探讨了零售商主导下,两制造商互相竞争的闭环供应链的决策及协调问题,研究发现制造商间竞争强度有利于促进新产品的销售以及废旧产品的回收,同时一定程度上可以增加供应链成员以及整体的利益。
针对零售商竞争的情形,Savaskan等[8]首先考虑到零售商之间的竞争强度对闭环供应链各成员决策的影响。Yanting H[9]则在其基础上分别构建了三种具有以旧换新策略的再制造模型,探讨了在零售商竞争的情形下以旧换新策略对供应链成员均衡决策和收益的影响。姚锋敏、滕春贤等[10]则考虑到供应链成员存在决策偏好,进一步研究了在一定竞争强度下两零售商的公平关切程度对供应链各成员收益的影响。
然而由于废旧产品再制造的利润较低,同时需要较高技术水平以及专业设备的支持。因此制造商以及零售商缺乏废旧产品回收再制造的积极性,需要外部环境的支持。彭志强等[11]探讨了不同补贴方式下新产品与再制品差别定价的闭环供应链定价决策,并通过数量折扣和收益共享契约协调该供应链。Wang等[12]研究了制造商和再制造商存在竞争和合作情况下,政府再制造补贴下新产品以及再制品的销售渠道选择问题。程发新等[13]从回收质量不确定的视角出发,研究了政府补贴第三方以及补贴制造商两种情况下废旧产品的回收质量对闭环供应链定价决策的影响。上述分析虽然将政府补贴纳入进来进行考量,然而却忽视了供应链成员之间的竞争行为。综上可见,政府补贴力度以及同层成员之间的竞争行为均会对供应链成员的利润造成影响,本文正是同时兼顾考虑了供应链同层成员的竞争行为以及政府补贴力度,从而对闭环供应链的定价决策和协调问题进行分析,这显然兼有理论与现实意义。
鉴于竞争强度与补贴力度的不确定性,下面的问题值得深思。当零售商之间存在竞争行为时,零售商之间的竞争强度是否会影响到闭环供应链各成员之间的利润分配?政府补贴力度又会对供应链决策造成怎样的影响?通过对上述问题的梳理,本文通过建立集中式决策和分散式决策模型探讨零售商的竞争强度和政府补贴力度对闭环供应链决策的影响,并设计收益共享风险共担契约对闭环供应链进行有效协调。最后通过算例分析对主要结论进行验证和说明。
1 模型描述与假设
在本文研究中,以两个零售商、单一生产制造商、第三方回收商以及政府构成的相应闭环供应链系统作为基础探讨相应的决策模型。此时一方面,由生产制造商完成新品与再造品的生产,而两个零售商则将这两种产品销售至终端用户。另一方面,第三方回收商又需要基于一定价格从终端用户手中对废旧产品进行回收并转移给生产制造商。同时为了提高各企业实行废旧产品再制造的积极性,政府将对生产制造商的废旧产品再制造过程给予一定补贴。具体如图1所示:
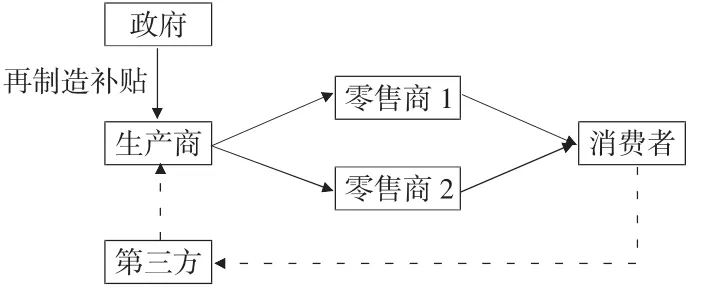
图1 政府补贴下两零售商竞争的闭环供应链系统结构图
因实际的生产系统复杂多样,在不影响结论的前提下,这里对复杂的前提加以中性化考虑,即提出如下假设。
(1)作为生产制造商能够借助于原料以及回收的废旧产品分别生产新品与再造品,新品和再造品不存在质量差异,由于新品的单位制造成本Cn高于再造品的单位制造成本Cr,因此生产制造商优先考虑使用回收的废旧产品进行生产。
(2)w为生产制造商向零售商批发该产品的价格,p1、p2分别为该产品在零售商1和零售商2处的销售价格。其中p1>w,p2>w。
(3)生产商按照a元的单价从第三方回收商处回购废旧产品,第三方回收商则按照每单位b元的价格从终端用户手中回购废旧产品,为了保证企业在废旧产品回收时有利可图,a>b。废旧产品的回收数量G=h+kb,其中h为终端用户无偿提供给第三方的废旧产品数量,k为价格敏感因子。
(4)零售商1和零售商2销售的产品在该消费市场中属于Bertrand价格竞争,根据姚峰敏学者的研究,提出了关于零售商i的需求函数。零售商1和零售商2的需求函数分别为D1=φ-p1+μp2,D2=φ-p2+μp1,其中φ为市场容量,μ为两零售商之间的竞争强度,0<μ<1,两零售商之间的竞争强度随着μ的增大而增大。
(5)废旧产品的回收数量小于该产品的市场需求量,即G<D1+D2。
(6)政府对生产制造商进行再制造补贴,对再造品进行每单位f元的补贴。
2 闭环供应链决策模型
2.1 集中式决策
在集中式决策方式下,闭环供应链的成员均是以整体收益最大化为目的。由此共同决定零售商1以及零售商2的新产品销售价格,同时还对废旧产品的回收价格进行明确,这三个指标分别为p1、p2、b。此时,集中式决策下供应链整体利润函数为:
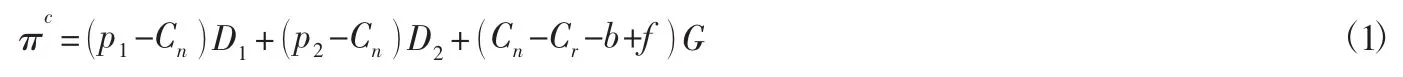
对公式(1)分别求p1,p2,b的一阶导得:


因为 0<μ<1,k>0,所以的海塞矩阵负定,是关于P1、P2以及b的严格凹函数,为此有着相应最优解。令得出零售商1和零售商2的最优新品销售价格,以及第三方的最优回收价格b。其具体算式为:

此时供应链的整体利润为:
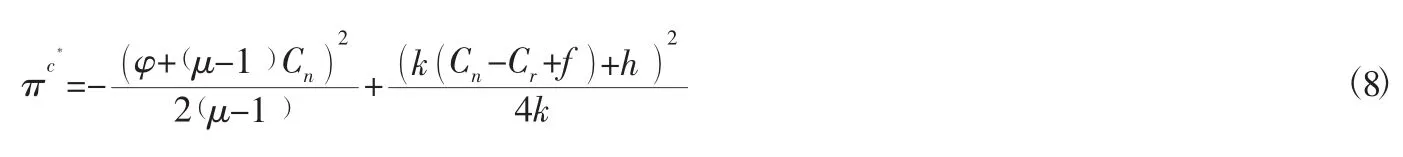
2.2 分散式决策
在分散式决策方式之下,供应链成员会最大限度实现个人利益最大化。所以,在此供应链中,生产商、零售商1、零售商2以及回收第三方的利润函数可以转换成:

在该闭环系统之中,生产制造商会成为整个供应链的核心,而零售商和第三方则扮演辅助角色,后者需要结合前者进行相应决策。
按照Stackelberg博弈步骤:第一,生产制造商会以利润最大化为目标制定产品的批发价w与回收价格a。第二,零售商1和零售商2按照生产商的定价,明确自身的产品销售价格;同时第三方给出废旧产品的收购价格b。
此处可以借助于逆向归纳法来进行计算,对上述式(10)、式(11)进行一阶求导得:

将其带入式(9),便能得到新品批发价w以及回收价格a的一阶导得:

在此基础上得到πm的海塞矩阵为:
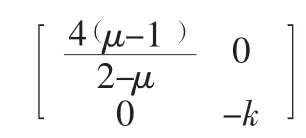
由于 0<μ<1,k>0,为此函数的海塞矩阵负定,存在最优解,将加以联立,得出新品的最优批发价以及最优废旧产品收购价格a。

从而得到零售商1和零售商2的新品最优销售价格以及废旧产品收购价格b。

将式 (17) 至式 (21) 带入至式 (9) 至式 (12) 得:
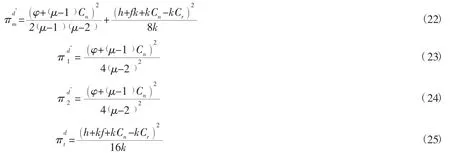
此时闭环供应链的整体利润为:

结论1:在政府补贴的两零售商相互竞争的闭环供应链系统中,集中决策下的闭环供应链的整体收益高于分散决策下的供应链整体收益。
结论1表明,分散式决策方式的决策会衍生出双重边际效应问题,为此需要对契约进行设计,从而实现供应链协调。

结论2表明在政府补贴的两零售商竞争的闭环供应链系统中,生产制造商、零售商、供应链整体的收益均与μ正相关。零售商之间的竞争行为有利于提高三者的收益。随着零售商之间竞争强度的增大,生产商、零售商以及供应链整体的收益均呈现上升趋势。
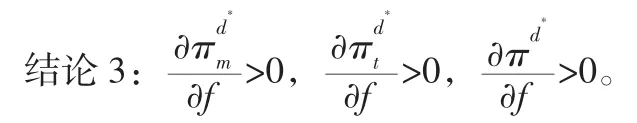
结论3表明在一定的情况下,政府补贴有利于提高生产商、回收第三方以及供应链整体的收益。同时随着补贴力度的增大,三者的收益也随之提高。
3 收益共享契约下的闭环供应链协调策略
通过设计收益共享契约,使其让整个供应链的收益达到集中式决策水平。两零售商会为制造商支付 (1- η1)p1D1与 (1- η1)p2D2,即部分新产品销售收入。制造商会为第三方支付 (1- η2)fG的政府补贴。此时制造商利润、两零售商利润以及第三方利润分别为:
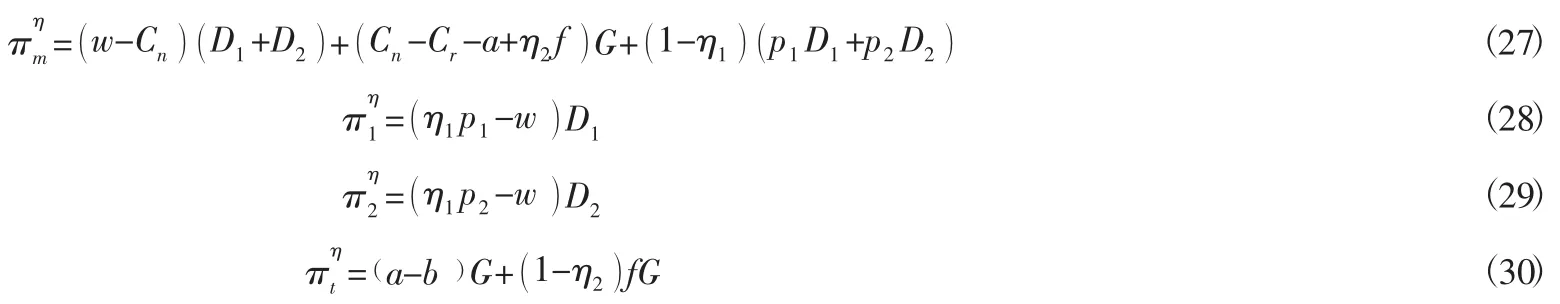
此处可以借助于逆向归纳法来进行计算,对上述式(27)、式(28)进行一阶求导得:

若是分散与集中方式的最优决策具有一致性,那么该闭环供应链得到协调,于是可得到对其求解得:

此时制造商的利润、两零售商的利润以及第三方的利润分别为:

为了保证契约的有效性,协调机制应满足约束条件:

求解可得η1,η2的取值区间分别为进而对式 (8) 与式(37) 进行比较可知即在引入收益共享契约之后,该闭环供应链总利润与集中决策之下的闭环供应链总利润相一致,因此该收益共享契约可以有效协调两零售商竞争下的分散式决策。
4 算例分析
为了进行更深入的研究,借助于Matlab软件工具对上述得到的模型进行算例分析,进而对上述给出的结论正确性进行验证。该模型的参数赋值为:φ=200,Cn=40,Cr=10,h=20,k=2.5,b=5,a=15,f=10。
首先在分散式决策下,对产品销售价格与批发价格进行数值仿真,具体数值如表1所示。
通过表1数值分析得出,伴随着两零售商之间竞争强度的提升,产品的批发价呈现出逐步上升之势,各零售商的销售价格也逐步上升。
其次,为了验证在该情形下竞争强度会对制造商、零售商利润会带来不同程度的影响,对该模型进行仿真,仿真结果如图2所示。
从图2可以看出在分散式决策下,伴随着对竞争强度的提升,对于制造商而言,他们的利润呈现逐渐上升,两零售商的利润也呈现一定的增长之势。该现象与结论2相符。

表1 不同竞争强度下产品的批发价格与销售价格
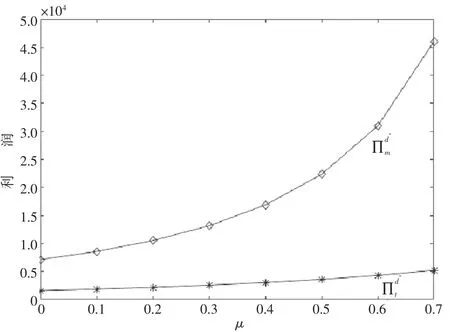
图2 基于不同竞争强度下制造商与零售商利润
通过模型仿真验证该情形得出,当竞争强度μ=0.5时,政府补贴力度会对制造商、第三方利润会带来不同程度的影响情况。
从图3,图4可以看出:随着政府补贴力度的提升,制造商与回收第三方的利润也随之上升。该现象与结论3相符。
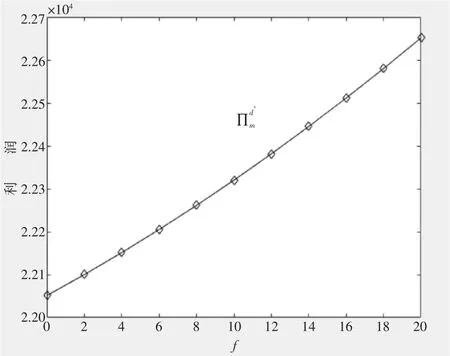
图3 基于不同补贴力度下制造商利润
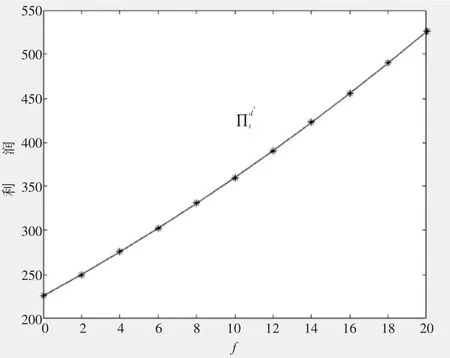
图4 基于不同补贴力度下第三方利润
5 总 结
零售商之间的竞争行为、政府补贴无疑已成为闭环供应链系统重要的因素,这对于科研与实践具有重要价值。通过上面先后构设的集中与分散式决策模型以及收益共享契约下的分散式决策模型,并就3种模型的对比,结合算例分析得到以下重要观点:
(1)在政府补贴的两零售商相互竞争的闭环供应链系统中,集中决策下的闭环供应链的整体收益高于分散决策下的供应链整体收益。
(2)两零售商之间的竞争行为有利于提高零售商、生产商以及供应链整体的收益。且随着零售商之间竞争强度的增加,制造商的收益逐渐增加,零售商的收益也呈现上升趋势。
(3)政府补贴有利于提高生产商和回收第三方的收益。且随着政府对废旧产品再制造补贴力度的增大,生产商、第三方以及供应链整体的收益也随之提高。
简言之,上述博弈模型的现实经济意义可以简单地理解为:收益共享契约和政府补贴能够有效提高供应链各成员的收益,提高闭环供应链各成员再制造活动的积极性,有助于加强生态文明建设,进一步实现绿色发展。同时,本文存在一定局限性,未来还可以进一步考虑消费者偏好以及回收质量对闭环供应链决策和协调的影响。
